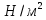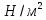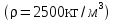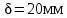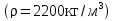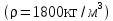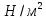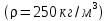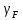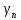Как определить расчетный пролет балки (плиты, перемычки)
При расчете любого изгибаемого элемента, будь то плита, балка или перемычка, прежде всего, следует определить расчетный пролет. При переводе объемных конструкций в плоскую расчетную схему очень важно задаться правильными размерами элементов. Ведь в расчетной схеме все просто: балка – это стержень, а опора – точка. На самом же деле опора имеет свой размер – глубину опирания, и балка не зависает на краях стены (от точки до точки), часть ее работает в пролете, но часть – «отдыхает» на опорах.
Создавая расчетную схему, мы сталкиваемся с двумя величинами: реальной длиной балки и расстоянием в свету между опорами. Какую из этих величин следует принять за расчетную? Если брать полную длину балки, это будет неверно, т.к. все-таки та ее часть, которая лежит на опоре, не подвержена таким напряжениям, как в пролете. Но брать за расчетную длину расстояние между опорами можно только в отдельных случаях, ниже мы рассмотрим, что да как.
Далеко не всегда расчетная длина балки совпадает с пролетом в свету между опорами.
Есть два варианта размера расчетного пролета.
1) Если опирание жесткое, т.е. балка защемлена на опоре (либо является частью монолитной конструкции), то расчетный пролет L0 равен расстоянию в свету между опорами.
2) Если же опирание шарнирное, то расчетный пролет всегда больше этого расстояния.
Рассмотрим глубже определение расчетного пролета при шарнирном опирании элемента. Во-первых, следует четко определиться с требованиями глубины опирания шарнирных элементов (поможет статья «В чем разница между шарнирным опиранием и жестким защемлением»). Если вы делаете расчет шарнирно опираемой железобетонной балки (плиты и т.п.), глубина ее опирания должна быть не более высоты сечения – иначе, это будет уже защемление или переходное состояние между шарниром и защемлением, а там и расчет другой, и длина расчетного пролета – согласно пункту 1. Т.е. если вы плиту толщиной 200 мм опираете на 450 мм с каждой стороны, то пользоваться нижеприведенным расчетом не следует.
Для ленивых во многих учебниках есть правило: L0 = 1.05L, т.е. берем расстояние между опорами в свету и умножаем на 1,05.
Но сейчас мы постараемся понять, в чем же суть увеличения расчетного пролета, и как поточнее его определить.
При расчете балки мы привыкли получать реакции на опоре в виде сосредоточенных сил.
Но если рассмотреть точнее, нагрузка от балки на опору передается в виде распределенной нагрузки, причем даже не равномерно распределенной: максимальная ее величина расположена у края опоры, а к концу балки она сходит на нет.
По общепринятым правилам перевода распределенной нагрузки в сосредоточенную, положение сосредоточенной нагрузки будет в центре тяжести треугольника, т.е. на расстоянии 1/3 от края опоры. В этом же месте будет расположена искомая реакция. А расстояние между этими реакциями будет равно расчетному пролету.
Таким образом, если глубина опирания балки с одной стороны равна А, а с другой стороны В, то расчетный пролет мы найдем по формуле:
L0 = L + A/3 + B/3.
Если же глубина опирания с двух сторон одинаковая и равна А, то
L0 = L + 2A/3.
Такое увеличение расчетного пролета по отношению к реальному (в районе 5%) дает определенный запас прочности и приближает нас к реальному положению вещей – ведь длина балки может быть разной, а глубина опирания обычно одинаковая. И пять процентов при трехметровом пролете значительно отличается от пяти процентов при восьмиметровом.
Надеюсь, статья оказалась вам полезной.
class=»eliadunit»>Добавить комментарий
Расчет многопролетной плиты монолитного перекрытия
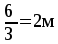 .
.Предварительно
задаются размером сечения балок:
второстепенная балка 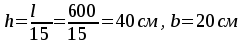 .
.
Расчетный
пролет и нагрузки. Расчетный
пролет плиты равен расстоянию в свету
между гранями ребер 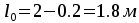
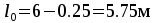 .
Отношение
пролетов
.
Отношение
пролетов 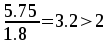 – плиту
рассчитывают как работающую по короткому
направлению. Принимаем толщину плиты
6 см.
– плиту
рассчитывают как работающую по короткому
направлению. Принимаем толщину плиты
6 см.Сбор нагрузок
Таблица 3- Нормативные и расчетные нагрузки на 1 кв.м перекрытия
Нагрузка | Норматиная
нагрузка, | Коэффициент надежности по нагрузке | Расчетная
нагрузка, |
Постоянная: Собственный
вес ребристой плиты | 1500 | 1.1 | |
То
же слоя цементного раствора | 440 | 1.3 | 570 |
То
же керамических плиток | 230 | 1.1 | 253 |
Равномерно распределенная нормативная нагрузка на перекрытия от массы пола и перегородок | 1500 | 1.1 | 1650 |
Итого: | 4680 | — | 4123 |
Временная: | 23500 | 1.2 | 28200 |
Полная: | 28180 | — | 32323 |
Для
расчета многопролетной плиты выделяют
полосу шириной 1м, при этом расчетная
нагрузка на 1м длины плиты  с
учетом
коэффициента
надежности
по
назначению
здания
с
учетом
коэффициента
надежности
по
назначению
здания 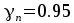 нагрузка
на 1м —
нагрузка
на 1м — 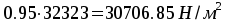
Изгибающие моменты для многопролетной плиты:
в средних пролетах и на средних опорах:
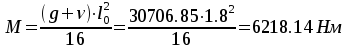 ,
,
в первом пролете и на первой промежуточной опоре
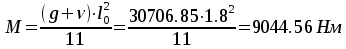 ,
,
Средние
пролеты плиты окаймлены по всему контуру
монолитно связанными с ними балками и
под влиянием возникающих распоров
изгибающие моменты уменьшаются на 20%,
если  .
При
.
При 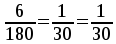
Характеристика
прочности бетона и арматуры. Бетон
тяжелый класса В15;
призменная прочность 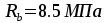 ,
прочность при осевом растяжении
,
прочность при осевом растяжении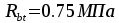 .
Коэффициент условий работы бетона
.
Коэффициент условий работы бетона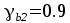 .
Арматура
— проволока класса Вр-II
диаметром 4мм в сварной рулонной сетке,
.
Арматура
— проволока класса Вр-II
диаметром 4мм в сварной рулонной сетке, 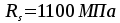
Подбор сечений продольной арматуры. В средних пролетах и на средних опорах h_0=h-a=6-1.2=4.8 см;
 ,
принимаем
,
принимаем 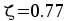 ,
,
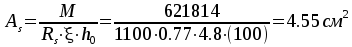 ,
принимаем
,
принимаем
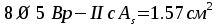 и
соответствующую рулонную сетку марки
и
соответствующую рулонную сетку марки 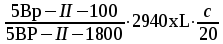 по сортаменту.
по сортаменту.
В
первом пролете и на первой промежуточной
опоре 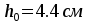
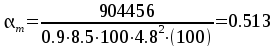 ,
принимаем
,
принимаем 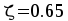 ,
,
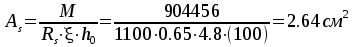 ,
принимаем
,
принимаем
и
соответствующую рулонную сетку марки 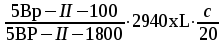 по сортаменту.
по сортаменту.
Расчет многопролетной второстепенной балки монолитного перекрытия
Расчетный
пролет и нагрузки. Расчетный
пролет равен расстоянию в свету между
главными балками 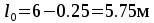 .
.
Сбор нагрузок
Таблица 4 — Расчетные нагрузки на 1 кв.м перекрытия
Нагрузка | Норматиная
нагрузка, | Коэффициент надежности по нагрузке | Расчетная
нагрузка, |
Постоянная: Собственный вес плиты | 4490 | 1.1 | 4940 |
То
же балки сечением 0.2х0.34 | 1700 | 1.1 | 1850 |
Итого: | 6190 | — | 6790 |
Временная: | 23500 | 1.2 | 28200 |
Полная: | 29690 | — | 34990 |
Расчетные усилия.Определим изгибающие моменты:
в первом пролете 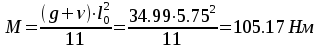 ,
,
на первой
промежуточной опоре 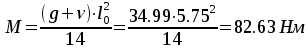 .
.
В средних пролетах и на средних опорах
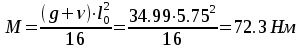 .
.
Отрицательные
моменты в средних пролетах определяют
по огибающей эпюре моментов. Они зависят
от отношения временной нагрузки к
постоянной 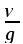 .
.
Врасчетном сечении в месте обрыва
надопорной арматуры отрицательный
момент при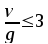 можно
принять равным 40% момента на первой
промежуточной опоре. Тогда отрицательный
момент в среднем пролете
можно
принять равным 40% момента на первой
промежуточной опоре. Тогда отрицательный
момент в среднем пролете .
Поперечные силы:
.
Поперечные силы:
на крайней опоре 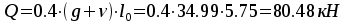 ,
,
на первой
промежуточной опоре слева 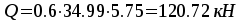 ,
,
на первой
промежуточной опоре справа 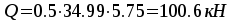 .
.
Характеристики
прочности бетона и арматуры. Бетон,
как и для плиты, класса В15. Арматура
продольная класса А-III
с 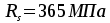 ,
поперечная — класса Вр-I
диаметром 5
мм с
,
поперечная — класса Вр-I
диаметром 5
мм с 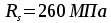 .
.
Определение
высоты сечения балки. Высоту
сечения подбирают по опорному моменту
при 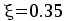 ,
поскольку на опоре момент определяют
с учетом образования пластического
шарнира. При
,
поскольку на опоре момент определяют
с учетом образования пластического
шарнира. При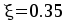 находят
находят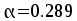 .
На опоре момент отрицательный — полка
ребра в растянутой зоне. Сечение работает
как прямоугольное с шириной ребра
.
На опоре момент отрицательный — полка
ребра в растянутой зоне. Сечение работает
как прямоугольное с шириной ребра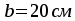 .
Вычисляем:
.
Вычисляем:
 ,
,
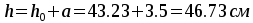 ,
принимаем h=50см,
b=20см,
тогда
,
принимаем h=50см,
b=20см,
тогда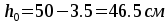 .
.
В
пролетах сечение тавровое — полка в
сжатой зоне. Расчетная ширина полки
при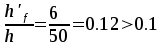 равна
равна 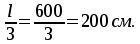
Расчет прочности по сечениям, нормальным к продольной оси. Сечение в первом пролете — М=105.17 кНм,
 ,
,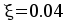 ,
,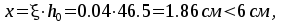 нейтральная
ось проходит в сжатой полке,
нейтральная
ось проходит в сжатой полке,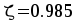 ,
, 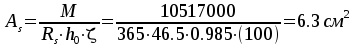 .
.
Принимаем 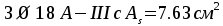 .
.
Сечение в среднем пролете — М=72.3 кНм,
 .
.
Принимаем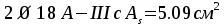 .На отрицательный
момент М=28.92 кНм сечение работает как
прямоугольное:
.На отрицательный
момент М=28.92 кНм сечение работает как
прямоугольное:
 ,
, 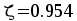 ,
,

Принимаем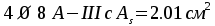 .
.
Сечение на первой промежуточной опоре — М=82.63 кНм. Сечение работает как прямоугольное:
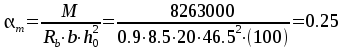 ,
,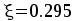 ,
,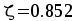 ,
,
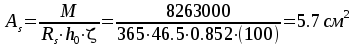
Принимаем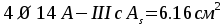 —
две гнутые сетки по
—
две гнутые сетки по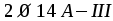 в
каждой.
в
каждой.
Сечение на средних опорах — М=72.3 кНм.
 ,
,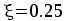 ,
,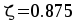 ,
,

Принимаем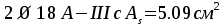 .
.
Расчет прочности второстепенной балки по сечениям, наклонным к продольной оси. Q=120.72 кН.
Диаметр
поперечных стержней устанавливаем из
условий сварки с продольными стержнями
d=18мм
и принимают 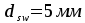 класса Вр-I,
класса Вр-I, 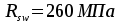 (с
учетом
(с
учетом  и
и 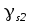 ).
Число каркасов — два,
).
Число каркасов — два,
 .
.
Шаг
поперечных стержней по конструктивным
условиям 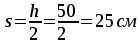 ,но не более 15см.
Для всех приопорных участков промежуточных
и крайних опор балки принят шаг s=15см.
В средней части пролета ~l/2
шаг
,но не более 15см.
Для всех приопорных участков промежуточных
и крайних опор балки принят шаг s=15см.
В средней части пролета ~l/2
шаг 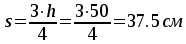 .
.
Вычисляем 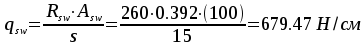 ,
влияние свесов сжатой полки
,
влияние свесов сжатой полки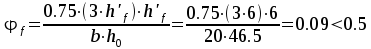 ,
,
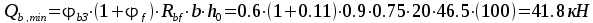 ,
,
условие 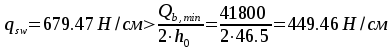 удовлетворяется.
удовлетворяется.
Требование 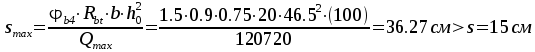 — удовлетворяется. При расчете прочности
вычисляют
— удовлетворяется. При расчете прочности
вычисляют
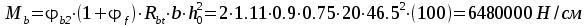 ,
,
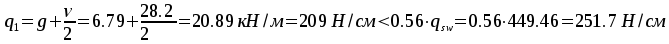 В
связи с этим вычисляют значение cпо формуле
В
связи с этим вычисляют значение cпо формуле
 ,
,
принимаем c=154.85см.
Тогда 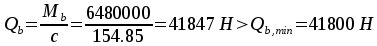 .Поперечная сила в вершине
наклонного сечения
.Поперечная сила в вершине
наклонного сечения 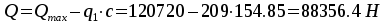 .
.
Длина
проекции расчетного наклонного сечения 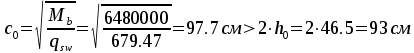 ,принимаем с=93 см. Вычисляем
,принимаем с=93 см. Вычисляем 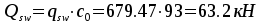 .
.
Условие прочности — выполняется.
Проверка
по сжатой наклонной полосе: 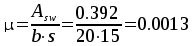 ,
,
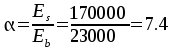 ,
, 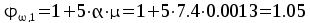 ,
,
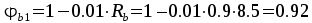 .
Условие
.
Условие

— удовлетворяется.
Установление размеров и расчетного пролета плиты
Предварительно задаемся сечением ригеля (рис. 3.1). Высота сечения h=600 мм, ширина сечения понизу b=600 мм, ширина сечения ребра (поверху) b’f=300мм, вылет полки с=150 мм.
Номинальная длина плиты Lп, конструктивная длина lп и расчетный пролет l0 определяются в соответствии с рис. 3.2.
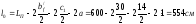
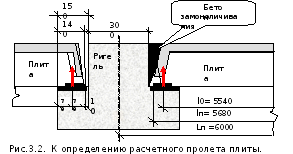
Здесь 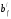 – ширина ригеля поверху, а-зазор между
торцом плиты и ригеля, принимаем, а=1 см,
с-вылет полки ригеля, с=150 мм, с1-длина
площадки опирания плиты, принята 14 см.
– ширина ригеля поверху, а-зазор между
торцом плиты и ригеля, принимаем, а=1 см,
с-вылет полки ригеля, с=150 мм, с1-длина
площадки опирания плиты, принята 14 см.
Конструктивная длина плиты
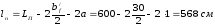
Высота
плиты 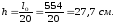 Принимаем
30 см, ширину продольных ребер понизу 7
см; поверху 9 см; ширину верхней полкиb’f = 161см; толщину сжатой полки
Принимаем
30 см, ширину продольных ребер понизу 7
см; поверху 9 см; ширину верхней полкиb’f = 161см; толщину сжатой полки 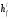 = 5 см. Толщина ребра расчетного таврового
сечения без учета заделки швов между
плитами принята 14 см. Сечение плиты
показано на рис. 3.3.
= 5 см. Толщина ребра расчетного таврового
сечения без учета заделки швов между
плитами принята 14 см. Сечение плиты
показано на рис. 3.3.
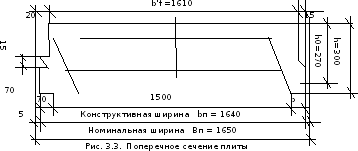
Расчетная ширина свеса полки в каждую сторону от ребра при отсутствии поперечных ребер должна быть:
не более 1/6 пролета плиты, 554/6 =92,33≈92см,
не более половины расстояния в свету между продольными ребрами (161 – 14)/2 = 73,5см, при hf / h = 5/30 = 0,167 > 0,1.
Таким образом, ширина полки, в расчете, равна 73,5·2+7·2 = 161 см.
Сбор нагрузок и определение усилий в плите
Таблица 1.
Сбор нагрузок на один квадратный метр плиты перекрытия
Вид нагрузки | Нормативная нагрузка, Н/м2 | Коэффициент надежности по нагрузке | Расчетная нагрузка, Н/м2 |
Постоянная: бетонное покрытие t = 20 мм, ρ = 22,0 кН/м3 цементная песчаная стяжка t = 40 мм; ρ = 18,0 кН/м3 засыпка (песок) 50мм ρ = 17,0 кН/м3 железобетонная ребристая плита | 440 720 850 2500 | 1,3 1,3 1,3 1,1 | 572 936 1105 2750 |
Итого | 4510 | – | 5363 |
в том числе: | 6000 4500 1500 | 1,2 1,2 1,2 | 7200 5400 1800 |
в том числе: | 10510 9010 1500 | – – – | 12563 10763 1800 |
Расчетная нагрузка вычисляется на 1м длины плиты с учетом коэффициента надежности по ответственности здания γn = 0,95 при ширине плиты 1,65 м.
Постоянная нагрузка g = 5363·0,95·1,65 = 8406,5 Н/м ≈ 8,41 кН/м.
Временная нагрузка v = 7200·0,95·1,65 = 11286 Н/м = 11,286 кН/м.
Полная q = 12563·0,95·1,65 = 19692,5 Н/м ≈ 19,7 кН/м.
Нормативная нагрузка на 1погонный метр плиты
постоянная gn = 4,51·0,95·1,65 ≈ 7,07 кН/м;
полная qn = gn +vn = 10,51·0,95·1,65 ≈ 16,47 кН/м;
постоянная и длительная 9,01·0,95·1,65 ≈ 14,12 кН/м.
Моменты и поперечные силы от расчетных и нормативных нагрузок вычисляются в соответствие с расчетной схемой и нагрузками.
Усилия для расчетов по предельным состояниям первой группы.
От расчетных нагрузок
кНм,
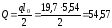 кН.
кН.
Усилия для расчетов по предельным состояниям второй группы.
От полной нормативной нагрузки
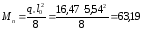 кНм
кНм
От постоянной и длительно-действующей части нормативной нагрузки
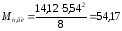 кНм.
кНм.
8 Расчет многопролётной плиты монолитного перекрытия
8.1 Расчётный пролёт и нагрузки
Расчётный пролёт
плиты равен расстоянию в свету между
гранями рёбер в средних пролётах  l0=3-0,2=2,8м,
в продольном направленииl0=6-0,25=5,75м.
Отношение пролётов 5,75/2,8=2,1>2 — плита
рассчитывается как работающая в коротком
направлении. Принимаем толщину плиты
6 см.
l0=3-0,2=2,8м,
в продольном направленииl0=6-0,25=5,75м.
Отношение пролётов 5,75/2,8=2,1>2 — плита
рассчитывается как работающая в коротком
направлении. Принимаем толщину плиты
6 см.
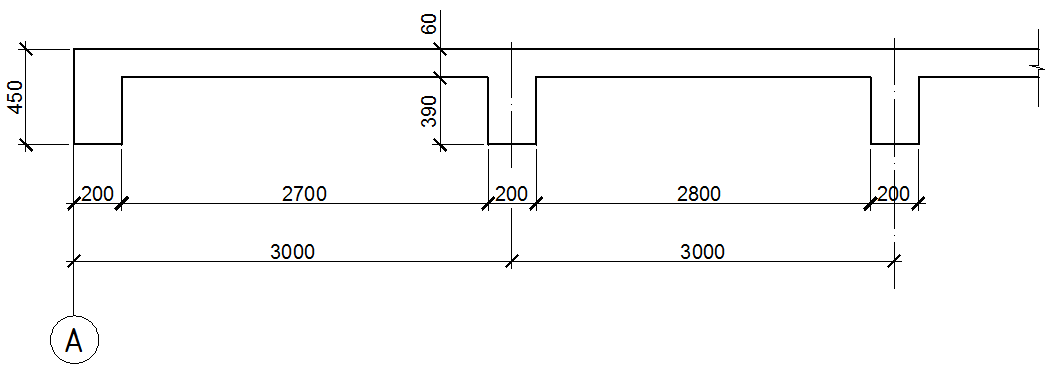
Рисунок 6. Монолитная плита ребристого перекрытия
Подсчёт нагрузок на 1м2перекрытия приведен в табл. 3.
Таблица 3
Нормативные и расчетные нагрузки на 1м2перекрытия
Вид нагрузки | Нормативная нагрузка, Н/м2 | Коэффициент надежности по нагрузке | Расчетная нагрузка, Н/м2 |
Постоянная: собственный вес плиты, δ=60 мм (ρ=2500 кг/м3) то же слоя цементного раствора δ=20 мм (ρ=2200 кг/м3) то же керамических плиток, δ=13 мм (ρ=1800 кг/м3) Итого | 1500 440 240 2180 | 1,1 1,3 1,1 — | 1650 570 264 2484 |
Временная В том числе: длительная кратковременная | 6000 1500 4500 | 1,2 1,2 1,2 | 7200 1800 5400 |
Полная нагрузка В том числе: постоянная и длительная кратковременная | 8180 3680 4500 | — — — | 9684 — — |
Полная расчётная нагрузка g+v=2484+7200=9684 Н/м2.
Для расчёта многопролётной плиты выделяем полосу шириной 1м, при этом расчётная нагрузка на 1м длины с учётом коэффициента γn=0,95 9684х0,95=9200 Н/м2
Изгибающие моменты для многопролётной плиты:
— в средних пролётах и на средних опорах
M=(g+v)∙l02/16=9200∙2,82/16=4508 Н∙м.
— в первом пролёте и на первой промежуточной опоре
M=(g+v)∙l02/11=9200∙2,82/11=6557 Н∙м.
Средние пролёты плиты окаймлены по контуру монолитно связанными с ними балками и под влиянием возникающих распоров изгибающие моменты уменьшаются на 20%, если h/l≥1/30. При 6/300=0,02<1/30 условеи не выполняется.
8.2 Характеристика прочности бетона и арматуры
Бетон тяжелый класса В15; призменная прочность Rb=8,5 МПа, прочность при осевом растяженииRbt=0,75 МПа. Коэффициент условий работы γb2=0,9. Арматура – проволока класса Вр-IIдиаметром 4 мм в сварной рулонной сетке,Rs=1145 МПа.

8.3 Подбор сечений продольной арматуры
В средних пролётах и на средних опорах h0=h-a=6-1,2=4,8 см.
αm=M/Rbbh02=450800/0,9∙8,5∙100∙4,82∙100=0,256, ζ=0,85.
As=M/Rs∙ζ∙h0=450800/1145∙0,85∙4,8∙100=0,96 см2.
Принимаем 84
Вр-IIсм2сAs=1,01
см2и соответствующую рулонную
сетку марки с
шагом 400 мм в продольном и 250 мм в поперечном
направлении.
с
шагом 400 мм в продольном и 250 мм в поперечном
направлении.
В первом пролёте и на первой промежуточной опоре h0=4,4 см.
αm=M/Rbbh02=655700/0,9∙8,5∙100∙4,42∙100=0,442, ζ=0,67.
As=M/Rs∙ζ∙h0=655700/1145∙0,67∙4,4∙100=1,94 см2.
Принимаем две сетки – основную и той же марки доборную с общим числом 164 Вр-IIиAs=2,02см2с шагом 400 мм в продольном и 250 мм в поперечном направлении.
9 Расчёт многопролётной второстепенной балки
9.1 Расчётный пролёт и нагрузки
Расчётный момент второстепенной балки равен расстоянию в свету между главными балками l0=6-0,25=5,75 м.
Расчётные нагрузки на 1 м длины второстепенной балки:
— постоянная:
собственного веса плиты и пола — 2,484∙3=7,45 кН/м;
то же балки сечением 0,2х0,39 (ρ=2500кг/м3), γf=1,1 — 2,06 кН/м;
итого – g=7,45+1,85=9,51 кН/м;
с учетом коэффициента надежности по назначению здания γn=0,95 –g=9,3·0,95=9,03 кН/м;
— временная с учетом γn=0,95 –v=7,2·3·0,95=20,52 кН/м;
— полная нагрузка g+v=9,03+20,52=29,55 кН/м.

Рисунок 7. К расчёту второстепенной балки
Установление размеров и расчетного пролета плиты
Предварительно задаемся сечением ригеля (рис. 3.1). Высота сечения h=600 мм, ширина сечения понизу b=600 мм, ширина сечения ребра (поверху) b’f=300мм, вылет полки с=150 мм.
Номинальная длина плиты Lп, конструктивная длина lп и расчетный пролет l0 определяются в соответствии с рис. 3.2.
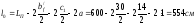
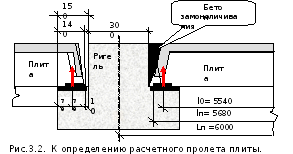
Здесь 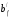 – ширина ригеля поверху, а-зазор между
торцом плиты и ригеля, принимаем, а=1 см,
с-вылет полки ригеля, с=150 мм, с1-длина
площадки опирания плиты, принята 14 см.
– ширина ригеля поверху, а-зазор между
торцом плиты и ригеля, принимаем, а=1 см,
с-вылет полки ригеля, с=150 мм, с1-длина
площадки опирания плиты, принята 14 см.
Конструктивная длина плиты
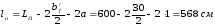
Высота
плиты 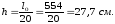 Принимаем
30 см, ширину продольных ребер понизу 7
см; поверху 9 см; ширину верхней полкиb’f = 161см; толщину сжатой полки
Принимаем
30 см, ширину продольных ребер понизу 7
см; поверху 9 см; ширину верхней полкиb’f = 161см; толщину сжатой полки 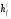 = 5 см. Толщина ребра расчетного таврового
сечения без учета заделки швов между
плитами принята 14 см. Сечение плиты
показано на рис. 3.3.
= 5 см. Толщина ребра расчетного таврового
сечения без учета заделки швов между
плитами принята 14 см. Сечение плиты
показано на рис. 3.3.

Расчетная ширина свеса полки в каждую сторону от ребра при отсутствии поперечных ребер должна быть:
не более 1/6 пролета плиты, 554/6 =92,33≈92см,
не более половины расстояния в свету между продольными ребрами (161 – 14)/2 = 73,5см, при hf / h = 5/30 = 0,167 > 0,1.
Таким образом, ширина полки, в расчете, равна 73,5·2+7·2 = 161 см.
Сбор нагрузок и определение усилий в плите
Таблица 1.
Сбор нагрузок на один квадратный метр плиты перекрытия
Вид нагрузки | Нормативная нагрузка, Н/м2 | Коэффициент надежности по нагрузке | Расчетная нагрузка, Н/м2 |
Постоянная: бетонное покрытие t = 20 мм, ρ = 22,0 кН/м3 цементная песчаная стяжка t = 40 мм; ρ = 18,0 кН/м3 засыпка (песок) 50мм ρ = 17,0 кН/м3 железобетонная ребристая плита | 440 720 850 2500 | 1,3 1,3 1,3 1,1 | 572 936 1105 2750 |
Итого | 4510 | – | 5363 |
в том числе: | 6500 4000 2500 | 1,2 1,2 1,2 | 7800 4800 3000 |
в том числе: | 11010 8510 2500 | – – – | 13163 10163 3000 |
Расчетная нагрузка вычисляется на 1м длины плиты с учетом коэффициента надежности по ответственности здания γn = 0,95 при ширине плиты 1,65 м.
Постоянная нагрузка g = 5363·0,95·1,65 = 8406,5 Н/м ≈ 8,41 кН/м.
Временная нагрузка v = 7800·0,95·1,65 = 12226,5 Н/м ≈ 12,23 кН/м.
Полная q = 13163·0,95·1,65 = 20663 Н/м ≈ 20,6 кН/м.
Нормативная нагрузка на 1погонный метр плиты
постоянная gn = 4,51·0,95·1,65 ≈ 7,07 кН/м;
полная qn = gn +vn = 11,01·0,95·1,65 ≈ 17,26 кН/м;
постоянная и длительная 8,51·0,95·1,65 ≈ 13,34 кН/м.
Моменты и поперечные силы от расчетных и нормативных нагрузок вычисляются в соответствие с расчетной схемой и нагрузками.
Усилия для расчетов по предельным состояниям первой группы.
От расчетных нагрузок
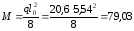 кНм,
кНм,
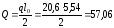 кН.
кН.
Усилия для расчетов по предельным состояниям второй группы.
От полной нормативной нагрузки
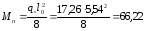 кНм
кНм
От постоянной и длительно-действующей части нормативной нагрузки
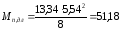 кНм.
кНм.
Расчёт и конструирование плиты перекрытия
РАСЧЁТ И КОНСТРУИРОВАНИЕ МОНОЛИТНЫХ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ МНОГОЭТАЖНОГО ПРОИЗВОДСТВЕННОГО ЗДАНИЯ.
Конструктивная схема перекрытия при
следующих исходных данных: размеры
здания в плане 36х21 м; высота этажа- 3,6 м;
наружные стены- кирпичные несущие- 640
мм; нормативная полезная нагрузка на
перекрытие 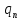 =
7 кПа.
=
7 кПа.
На основании требований и рекомендаций принимаем:
— четыре пролёта главных балок с размерами: 9,0 м;
— три пролёта второстепенных балок с размерами: 7,0 м;
Исходя из этого ширина плит принимается равной 2,25 м.
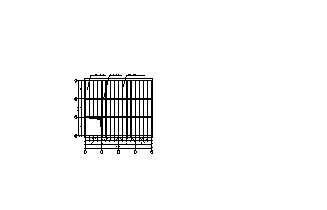
Рис 1.2 Конструктивная схема перекрытия
Принимаем следующие размеры несущих конструкций:
—
толщина плиты при нормативной нагрузке
7 кПа-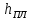 =80
мм;
=80
мм;
—
высота главной балки 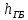 =0,6
м;
=0,6
м;
—
ширина главной балки 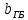 =0,3
м;
=0,3
м;
—
высота второстепенной балки  =0,35
м;
=0,35
м;
—
ширина второстепенной балки 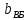 =0,18
м;
=0,18
м;
— поперечное сечение колоны 400х400 мм.
Элементы железобетонного монолитного ребристого перекрытия (плиту, второстепенную и главную балку) рассчитываем отдельно. Расчёт элементов производится в соответствии с указаниями СНБ 5.03.01-02 [1,2,12,13].
Класс бетона по прочности на сжатие при проектировании монолитных ребристых перекритий принимается по таблице в зависимости от класса по условиям эксплуатации конструкции (табл.. 5.2, 11.12 ) [1,2,13].
Монолитную плиту и балки проектируют из бетона одного класса. Клас арматуры принимаем S400.
Подсчёт нагрузок на отдельные элементы перекрытия, несмотря на на его монолитность, ведётся как для разрезных конструкций.
Для балочных плит повышение несущей способности, обусловленное опирание по коротким сторонам ,относительно невелико. Поэтому для расчёта балочной плиты на равномерно распределённую нагрузку из неё условно выделяется полоса шириной 1м, опёртая на второстепенные балки. Принимается, что такая полоса работает как отдельная неразрезная балка и изгибается в одном направлении.
2.1 Определение нагрузок
Нагрузки
на 1 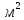 плиты перекрытия складывается из
постоянной нагрузки (от собственной
массы плиты и заданной конструкции
пола) и переменной (полезной), принимаемой
по заданию. Для определения расчётных
нагрузок коэффициенты безопасности по
нагрузке определяются по СНиП 2.01.07-85
«На грузки и воздействия» и СНБ 5.03.01-02
«Бетонные и железобетонные конструкции»
плиты перекрытия складывается из
постоянной нагрузки (от собственной
массы плиты и заданной конструкции
пола) и переменной (полезной), принимаемой
по заданию. Для определения расчётных
нагрузок коэффициенты безопасности по
нагрузке определяются по СНиП 2.01.07-85
«На грузки и воздействия» и СНБ 5.03.01-02
«Бетонные и железобетонные конструкции»
Определение
нагрузок на 1 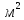 перекртия приведено в таблице 2.1. Состав
перекрытия показан на рис.2.1
перекртия приведено в таблице 2.1. Состав
перекрытия показан на рис.2.1
Рис 2.1 Состав перекрытия
Таблица 2.1
№ | Наименование нагрузки | Норма-тивное
значение, кН/ |
|
| Расчётное
значение, кН/ |
Постоянная нагрузка | |||||
1 | Цем.
раствор δ=30 мм, ρ=22 кН | 0,66 | 1,2 | 1,05 | 0,832 |
2 | Гидроизоляция | — | — | — | — |
3 | Монолитная
железобетонная плита перекрытия δ=80
мм, ρ=25кН | 2 | 1,1 | 1,05 | 2,31 |
Итого: g=3,142 | |||||
Переменная нагрузка Полезная нагрузка | 7,0 | 1,2 | 1,05 | 8,82 | |
Итого: q=11,962 | |||||
Для
выполнения расчёта принимаем полосу
плиты шириной, равной 1 м. Таким образом,
нагрузка на 1 пог. м полосы будет равна
нагрузке, приходящейся на 1  плиты.
плиты.
Определение расчётных усилий
Плита рассматривается как неразрезная балка, загруженная равномерно распределённой нагрузкой. В неразрезных балочных плитах с равными пролётами или с пролётами отличающимися не более чем на 20% изгибающие моменты определяют с учётом перераспределения усилий (изгибающих моментов) в следствии пластических деформаций бетона по готовым формулам.
На работу участков плиты, защемлённым по четырём сторонам, в местах сопряжения с второстепенными и главными балками, значение изгибающих моментов следует уменьшить в сечениях промежуточных пролётов и промежуточных опор на 20%.
Расчёт следует выполнять для двух полос, условно вырезанных у торцевой стены (участки плиты защемлены по трём сторонам и свободно опёрты одной стороной на стену- полоса I) и в средней части перекрытия (участки плиты защемлены по четырём сторонам- полоса II) (рис. 2.2)
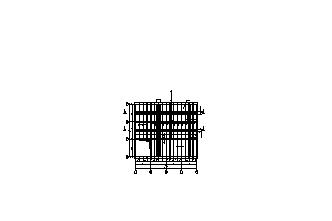
Рис 2.2 План монолитного перекрытия
За расчётные пролёты плиты принимаются:
— среднее – расстояние в свету между второстепенными балками;
— крайние – расстояние от середины площадки опирания плиты на стену (при опирании на наружные стены) до ближайшей к стене грани ребра второстепенной балки (рис. 2.3)
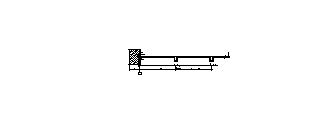
Рис. 2.3 Расчётные пролёты плиты перекрытия
Длина участка опирания плиты на кирпичную наружную стену принимается равной 100 мм (рис. 2.3)
Значение расчётных изгибающих моментов определяют по формулам:
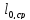 =
=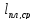 —
—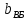 =2250-180=2070
мм
=2250-180=2070
мм
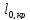 =
=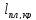 +
+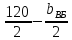 =2250+
=2250+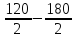 =2220
мм
=2220
мм
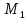 =
=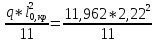 =5,36 кНм;
=5,36 кНм;
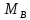 =
=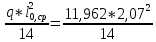 =3,66 кНм;
=3,66 кНм;
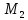 =
=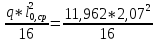 =3,02 кНм;
=3,02 кНм;
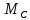 =
=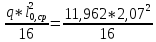 =3,02 кНм;
=3,02 кНм;
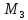 ==3,02 кНм;
==3,02 кНм;
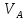 =0,4*q*l0,кр=0.4*11,962*2,22=10,62
кН
=0,4*q*l0,кр=0.4*11,962*2,22=10,62
кН
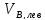 =0,6*q*l0,кр=0,6*11,962*2,22=15,93
кН
=0,6*q*l0,кр=0,6*11,962*2,22=15,93
кН
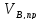 =0,5*q*l0,ср =0.5*11,962*2,07=12,38 кН
=0,5*q*l0,ср =0.5*11,962*2,07=12,38 кН
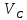 =0,5*q*l0,ср =0.5*11,962*2,07=12,38 кН
=0,5*q*l0,ср =0.5*11,962*2,07=12,38 кН