Расчет уголка на прогиб и изгиб
Калькулятор
| Пример расчета |
Калькуляторы по теме:
- Сбор нагрузок на балки перекрытия онлайн.
- Расчет прямоугольной трубы
- Расчет квадратной трубы
- Расчет двутавра
- Расчет швеллера
- Расчет деревянной балки
Швеллер в наличии на складе в Москве
Швеллер является продукцией прокатного производства, которая имеет U-образное поперечное сечение. В зависимости от технологии производства, швеллеры бывают горячекатаные и гнутые.
Размеры и форма г/к швеллеров общего назначения регламентируются стандартом ГОСТ 8240-97. Ширина проката согласно указанному нормативному документу может быть от 32 до 115 мм, а высота 50 — 400 мм.
В обозначении номера профиля зашифрована высота швеллера в сантиметрах (цифра) и серия или тип профиля (буква).
Размеры гнутого швеллера регламентируются стандартом ГОСТ 8278-83. В соответствии этому документу высота профиля может принимать значение от 25 до 410 мм, толщина швеллера – от 2 до 8 мм, и ширина может быть 26 — 160 мм.
В APEX METAL вы сможете приобрести швеллер наиболее востребованных размеров из стали марок Ст3 и 09Г2С:
- серии П с параллельными гранями — типоразмеры профиля 5П — 30П;
- серии У с уклоном граней — типоразмеры профиля 6,5У — 30У;
- гнутый швеллер с размерами от 50х40х3 до 250х125х6.
Значения высоты и ширины полки, ширины и толщины стенки по ГОСТ 8240-97 смотрите на странице — Как правильно расшифровать условное обозначение швеллера.
Инструкция к калькулятору
Обращаю ваше внимание, что в нецелых числах необходимо ставить точку, а не запятую, то есть, например, 5.7 м, а не 5,7. Также, если что-то не понятно, задавайте свои вопросы через форму комментариев, расположенную в самом низу.
Исходные данные
Расчетная схема:
Длина пролета (L) — расстояние между двумя опорами или от жесткой заделки до края консоли.
Расстояния (А и В) — расстояния от опор до места приложения сил. В случае с 3-ей схемой — расстояние от опоры до края консоли.
В случае с 3-ей схемой — расстояние от опоры до края консоли.
Нормативная и расчетная нагрузки — нагрузки, которые действуют на уголок, выраженные в кг/м или кг.
Fmax — максимально допустимый прогиб для балки, применяемый в той или иной конструкции. Можно найти в таблице Е.1 приложения Е СНиПа 2.01.07-85* (СП 20.13330.2011) «Нагрузки и воздействия». Данный показатель для наиболее часто встречающегося случая представлен в таблице 1.
Количество уголков — если Вы собираетесь в качестве балки использовать два спаренных уголка, то нужно выбирать «два», в противном случае «один».
Характеристики стали:
Расчетное сопротивление (Ry) — подбирается в зависимости от марки стали. Но чаще всего проектировщики принимают Ry = 210 МПа. Остальные см. таблицу 2.
Размеры уголка — выбирается предполагаемый размер равнополочного и (или) неравнополочного уголка.
Расположение — выбирается для неравнополочного уголка в зависимости от того, как он будет работать.
По Х — если нагрузка будет приходиться на короткую полку.
По Y — если нагрузка будет приходиться на длинную полку.
Особенности
Имеет Г-образный профиль. Изготавливается из углеродистой либо нержавеющей стали посредством горячей прокатки. Последняя и прокат с оцинкованным покрытием используется для изготовления конструкций, работающих в условиях агрессивного воздействия.
В зависимости от соотношения длин полок стальные уголки в таблице делятся на равнополочные и неравнополочные. У первых они равны. У вторых – отличаются. На профилегибочных станках из листовой стали холодной и горячей прокатки формируется уголок с «гнутым» профилем. Его изготовление осуществляется на прессе с формированием округлой поверхности в месте изгиба.
Для стального уголка, размеры которого представлены в таблице, регламентируется отклонение от формы. Кривизна до 0,4% длины. Точность проката может отличаться. Выделяют тип «А» с высокой точностью и тип «Б» с обычной.
Сортамент горячекатаного уголка
Высокая прочность этой продукции обеспечивает ее применение для создания конструкций, работающих под воздействием серьезных нагрузок. Сортамент равнополочного горячекатаного уголка регламентируется ГОСТом 8509-93. Стандартом предусмотрены два класса точности прокатки:
- А — повышенной;
- В — обыкновенной.
В производстве углового проката используется углеродистая сталь обыкновенного качества и качественная конструкционная. Для изготовления ответственных конструкций и элементов машин и механизмов используют уголок из низколегированных сталей типа 09Г2С, 10ХСНД. Такая продукция может эксплуатироваться в широком диапазоне температур (-70…+450°C), поэтому востребована в регионах с суровым климатом.
Таблица размеров и массы наиболее распространенного сортамента стального равнополочного уголка по ГОСТу 8509-93
| Ширина полки, мм | Толщина полки, мм | Масса 1 метра, кг | Ширина полки, мм | Толщина полки, мм | Масса 1 метра, кг |
| 20 | 3 | 0,89 | 63 | 4 | 3,9 |
| 4 | 1,15 | 5 | 4,81 | ||
| 25 | 3 | 1,12 | 6 | 5,72 | |
| 4 | 1,46 | 70 | 5 | 5,38 | |
| 30 | 3 | 1,36 | 6 | 6,39 | |
| 4 | 1,78 | 7 | 7,39 | ||
| 35 | 3 | 1,6 | 75 | 5 | 5,8 |
| 4 | 2,1 | 6 | 6,89 | ||
| 5 | 2,58 | 7 | 7,96 | ||
| 40 | 3 | 1,85 | 8 | 9,02 | |
| 4 | 2,42 | 80 | 6 | 7,36 | |
| 5 | 2,98 | 7 | 8,51 | ||
| 45 | 3 | 2,08 | 8 | 9,65 | |
| 4 | 2,73 | 90 | 7 | 9,64 | |
| 5 | 3,37 | 8 | 10,93 | ||
| 50 | 3 | 2,32 | 9 | 12,2 | |
| 4 | 3,05 | 100 | 7 | 10,79 | |
| 5 | 3,77 | 8 | 12,25 | ||
| 6 | 4,47 | 10 | 15,1 |
Расчет уголка на прогиб и изгиб
Данный онлайн-калькулятор предназначен для того, чтобы Вы могли легко и быстро подобрать размеры уголка в зависимости от приходящейся на него нагрузки. Особенность его в том, что на одной странице возможно сравнение равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков. Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.
Особенность его в том, что на одной странице возможно сравнение равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков. Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.
Расчет уголков производится на изгиб и прогиб (по прочности и по деформациям) для следующих расчетных схем:
- Тип 1 – однопролетная шарнирно-опертая балка с равномерно распределенной нагрузкой. Пример: перемычка из уголка, которая несет плиты перекрытия и небольшую высоту кладки. (Подробнее о расчете перемычек из уголка см. этот калькулятор).
- Тип 2 – консольная балка с жесткой заделкой с равномерно распределенной нагрузкой. Пример: железобетонный козырек, выполненный с применением уголка, который жестко (с применением ребер жесткости, ограничивающих любые повороты) приварен к железобетонной стене.
- Тип 3 – однопролетная шарнирно-опертая балка с консолью с равномерно распределенной нагрузкой.
 Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).
Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).
- Тип 4 – однопролетная шарнирно-опертая балка с одной сосредоточенной силой. Пример: перемычка, на которую опирается одна балка перекрытия.
- Тип 5 – однопролетная шарнирно-опертая балка с двумя сосредоточенными силами. Пример: перемычка, на которую опираются две сосредоточенные силы.
- Тип 6 – консольная балка с одной сосредоточенной силой. Пример: козырек дома с кирпичной стенкой на нем, построенного в африканской республике (где никогда не выпадает снег) по фантазии африканского архитектора. Уголки этого козырька жестко заделаны в стену, так как описано во второй схеме.
Примечание: рассчитываемый уголок на рисунках с примерами окрашен в красный цвет.
Расчет уголка на прогиб и изгиб
С помощью данного калькулятора Вы можете не только легко рассчитать уголок на прогиб и изгиб, но и подобрать оптимальный из равнополочного и неравнополочного уголков.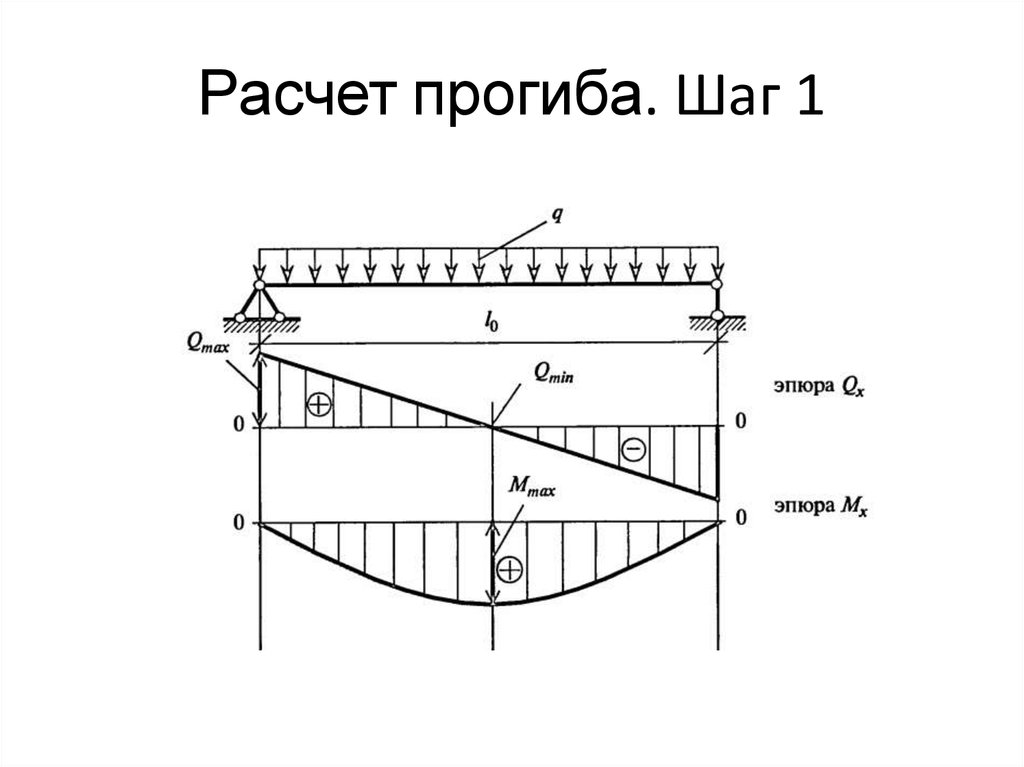
Применение стальных уголков
Используются стальные уголки повсеместно, так как они прекрасно поддаются сварке, прочные, способны выдержать большие нагрузки, имеют технологичную форму.
В основном уголки применяют в строительстве, где они являются элементами несущих металлоконструкций (ферм, перекрытий, пролетов и пр.).
Стальной профиль уголка имеет форму, которая удобна при производстве оконных (дверных) проемов. А для арок и иных изогнутых конструкций используется неравнополочный уголок, у которого различный момент сопротивления к осям.
Каркас мебели усиливают посредством уголков небольшого типоразмера, а декорирование интерьера — с помощью нержавеющих уголков.
Широкое распространение получил стальной уголок и в машиностроении. Он используется для создания вагонов, автотранспорта, специализированной техники большого размера.
В ходе проведения электромонтажных работ стальной уголок применяется для закрепления кабеля и оборудования. В случае больших нагрузок применяется изделие из низколегированной стали.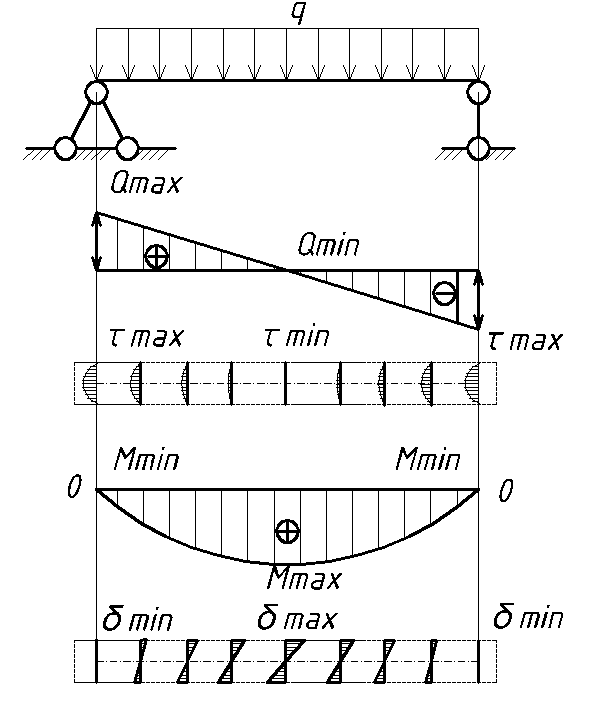 Такие же профили используются для защиты конструкций от влажности и прочих агрессивных условий окружающей среды.
Такие же профили используются для защиты конструкций от влажности и прочих агрессивных условий окружающей среды.
Помимо указанного, стальные уголки применяются:
- В хозяйственном строительстве — при возведении парников и больших теплиц, беседок (как переносных, так и стационарных), ограждений.
- При установке лестниц — для монтажа рам ступенек, опор для крыльца, перил. Уголки используются для строительства наружных и внутренних лестничных конструкций.
- При создании качелей, лавок, столов и прочей уличной мебели, навесов для защиты от непогоды, калиток и въездных ворот, а также при монтаже решеток, защищающих окна и двери.
- При изготовлении складских и производственных стеллажей, верстаков и каркасов для шкафов, испытательных и сборочных стендов.
- В домашнем хозяйстве — для создания каркасов кирпичных печей и дверей из металла.
Стальные уголки получили широкое применение в промышленности благодаря таким преимуществам материала, из которого они делаются, как высокая прочность при малой массе, долгий срок службы из-за стойкости к коррозии, удобства хранения (укладки), сборки и транспортировки.
Характеристики горячекатаного металлического уголка
Равнополочный горячекатаный стальной уголок производят в соответствии с ГОСТом 8509-93 из квадрата, являющегося исходной заготовкой. Наиболее массово используется угловой профиль обычной точности «В», для ответственных конструкций – продукция высокой точности «А». Размеры полки, согласно стандарту, – от 20 до 250 мм.
Сортамент неравнополочных уголков определяется ГОСТом 8510-86. Наименьшие размеры полок – 16 и 25 мм, максимальные – 125 и 200 мм. Эта продукция применяется при создании конструкций сложной формы, например, арок.
Для горячекатаной продукции характерна высокая прочность, что позволяет использовать ее в конструкциях, предназначенных для работы в условиях высоких нагрузок. В производстве углового профиля массово используют углеродистую сталь обыкновенного качества и качественную. Изделия из низколегированных сталей применяют для создания конструкций ответственного назначения корпусов, рам и других деталей сельскохозяйственной техники, локомотивов, вагонов, крупногабаритных строительных машин и механизмов. Изделия из такого профиля могут сохранять рабочие характеристики в широком температурном интервале – от -70° до +70°C, при серьезных суточных и сезонных температурных перепадах.
Изделия из такого профиля могут сохранять рабочие характеристики в широком температурном интервале – от -70° до +70°C, при серьезных суточных и сезонных температурных перепадах.
Горячекатаную продукцию поставляют партиями, размер которых обычно не превышает 70 тонн. Каждая партия имеет сертификат соответствия требованиям нормативной документации.
Расчет количества стального равнополочного уголка
При определении массы партии проката углового профиля необходимо знать массу погонного метра, которую вы можете определить по таблице, и общий метраж.
Характеристики гнутого стального уголка
Эту продукцию получают на профилегибочных станках из горяче- или холоднокатаного листового проката. Процесс проходит без нагрева. В холодногнутой продукции сохраняются остаточные напряжения, ухудшающие рабочие свойства. Для устранения остаточных явлений применяют отпуск – нагрев до определенной температуры с последующим медленным охлаждением. Визуальное отличие двух видов продукции: горячекатаный уголок имеет четкий прямой внешний угол, для гнутого характерен скругленный угол.
Размеры металлического равнополочного гнутого уголка определяются ГОСТом 19771-93, неравнополочного – ГОСТом 19772-93. Эта продукция имеет меньшую прочность, по сравнению с горячекатаной. Применяется в мебельном производстве, в качестве ребер жесткости, вспомогательных элементов при креплении конструкций, для изготовления деталей машин и механизмов.
Расчет стального уголка | Характеристики гнутого металлического уголка
Стальной уголок – наиболее востребованный вид фасонного проката. По способу производства он разделяется на горячекатаный и гнутый. Исходные материалы: углеродистые стали обыкновенного качества Ст3 пс/сп (для рядового применения), качественные, низколегированные 09Г2С, 17Г1С, 10ХСНД, 15 ХСНД (для изделий, используемых при повышенных нагрузках, в сложных температурных условиях, при контакте с агрессивными средами).
Характеристики горячекатаного металлического уголка
Равнополочный горячекатаный стальной уголок производят в соответствии с ГОСТом 8509-93 из квадрата, являющегося исходной заготовкой. Наиболее массово используется угловой профиль обычной точности «В», для ответственных конструкций – продукция высокой точности «А». Размеры полки, согласно стандарту, – от 20 до 250 мм.
Наиболее массово используется угловой профиль обычной точности «В», для ответственных конструкций – продукция высокой точности «А». Размеры полки, согласно стандарту, – от 20 до 250 мм.
Сортамент неравнополочных уголков определяется ГОСТом 8510-86. Наименьшие размеры полок – 16 и 25 мм, максимальные – 125 и 200 мм. Эта продукция применяется при создании конструкций сложной формы, например, арок.
Для горячекатаной продукции характерна высокая прочность, что позволяет использовать ее в конструкциях, предназначенных для работы в условиях высоких нагрузок. В производстве углового профиля массово используют углеродистую сталь обыкновенного качества и качественную. Изделия из низколегированных сталей применяют для создания конструкций ответственного назначения корпусов, рам и других деталей сельскохозяйственной техники, локомотивов, вагонов, крупногабаритных строительных машин и механизмов. Изделия из такого профиля могут сохранять рабочие характеристики в широком температурном интервале – от -70° до +70°C, при серьезных суточных и сезонных температурных перепадах.
Горячекатаную продукцию поставляют партиями, размер которых обычно не превышает 70 тонн. Каждая партия имеет сертификат соответствия требованиям нормативной документации.
Расчет количества стального равнополочного уголка
При определении массы партии проката углового профиля необходимо знать массу погонного метра, которую вы можете определить по таблице, и общий метраж.
Таблица весов равнополочного стального горячекатаного уголка наиболее распространенных размеров
|
Размер полки, мм |
Толщина стенки, мм |
Масса 1 м, кг |
Размер полки, мм |
Толщина стенки, мм |
Масса 1 м, кг |
Размер полки, мм |
Толщина стенки, мм |
Масса 1 м, кг |
|
20 |
3 |
0,89 |
35 |
4 |
2,1 |
50 |
4 |
3,05 |
4 |
1,15 |
5 |
2,58 |
5 |
3,77 |
|||
|
25 |
3 |
1,12 |
40 |
3 |
1,85 |
6 |
4,47 |
|
|
4 |
1,46 |
4 |
2,42 |
63 |
4 |
3,9 |
||
|
30 |
3 |
1,36 |
5 |
2,98 |
5 |
4,81 |
||
|
4 |
1,78 |
45 |
3 |
2,08 |
6 |
5,72 |
||
|
32 |
3 |
1,46 |
4 |
2,73 |
70 |
5 |
5,38 |
|
|
4 |
1,91 |
5 |
3,37 |
6 |
6,39 |
|||
|
35 |
3 |
|
50 |
3 |
2,32 |
7 |
7,39 |
Характеристики гнутого стального уголка
Эту продукцию получают на профилегибочных станках из горяче- или холоднокатаного листового проката. Процесс проходит без нагрева. В холодногнутой продукции сохраняются остаточные напряжения, ухудшающие рабочие свойства. Для устранения остаточных явлений применяют отпуск – нагрев до определенной температуры с последующим медленным охлаждением. Визуальное отличие двух видов продукции: горячекатаный уголок имеет четкий прямой внешний угол, для гнутого характерен скругленный угол.
Процесс проходит без нагрева. В холодногнутой продукции сохраняются остаточные напряжения, ухудшающие рабочие свойства. Для устранения остаточных явлений применяют отпуск – нагрев до определенной температуры с последующим медленным охлаждением. Визуальное отличие двух видов продукции: горячекатаный уголок имеет четкий прямой внешний угол, для гнутого характерен скругленный угол.
Размеры металлического равнополочного гнутого уголка определяются ГОСТом 19771-93, неравнополочного – ГОСТом 19772-93. Эта продукция имеет меньшую прочность, по сравнению с горячекатаной. Применяется в мебельном производстве, в качестве ребер жесткости, вспомогательных элементов при креплении конструкций, для изготовления деталей машин и механизмов.
Рассчитываем вес уголка с помощью калькулятора
Скачать калькулятор уголка онлайн и бесплатно получить код можно на этой странице
Виды уголковПрокатная промышленность выпускает разные виды прокатных профилей. Одним из них является уголок. Этот вид продукции имеет профиль в виде буквы Г и угол 90 градусов на сгибе двух полок. В качестве материала, из которого изготавливается уголок, могут служить различные металлы. Это может быть углеродистая сталь, нержавеющая сталь, например 17Х18Н9, 06ХН28МДТ, 12Х17, дюралюминий, титан, медь, свинец и даже золото.
Этот вид продукции имеет профиль в виде буквы Г и угол 90 градусов на сгибе двух полок. В качестве материала, из которого изготавливается уголок, могут служить различные металлы. Это может быть углеродистая сталь, нержавеющая сталь, например 17Х18Н9, 06ХН28МДТ, 12Х17, дюралюминий, титан, медь, свинец и даже золото.
По виду уголок может быть равнополочным, изготавливаемый из листа. Как следует из названия, обе полки в таком уголке одинакового размера. Способы изготовления предусматривают как горячий и холодный. При изготовлении лист кроится на полосы заданной ширины и длины. Заготовки затем пропускаются через машины для гибки профиля, пропуская их в несколько этапов, постепенно доводя угол изгиба уголка до 90 градусов.
Этот вид проката прекрасно работает на изгиб и растяжение. Такой вид деформации, как скручивание для этого профиля не применяют.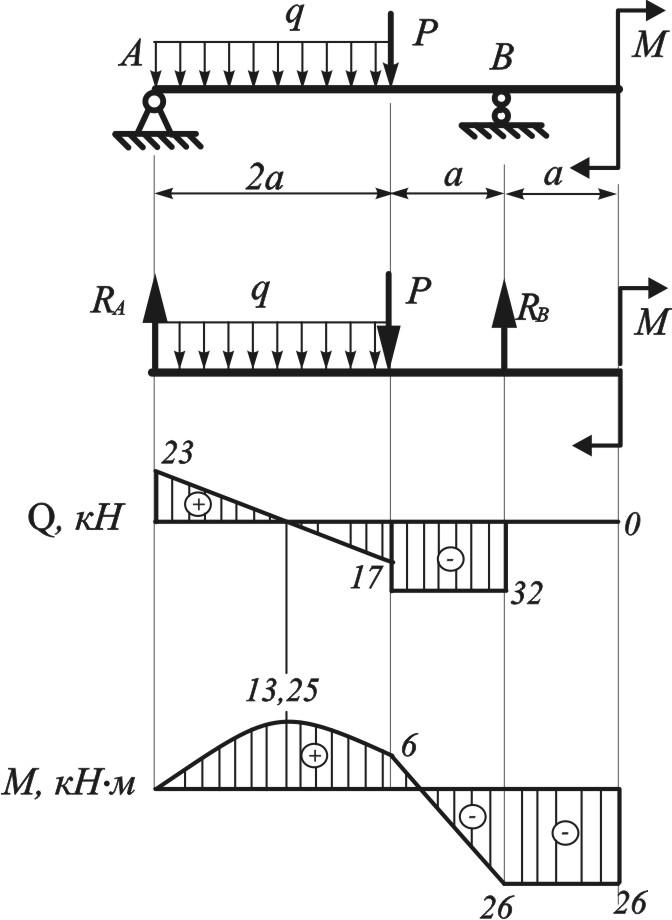
Другой вид уголка – неравнополочный, что также понятно из названия, изготавливаемый методом проката горячего металла из болванки, отлитой непрерывным способом.
Эта болванка, нагретая до температуры 1200 градусов, проходит через ряд станков с гибочными валами, которые постепенно деформируют заготовку, доведя её до нужного профиля и размера. Затем заготовка переходит для окончательной обработки и доводки на специальные правильные машины.
Готовый уголок разрезают на нужную длину. Этот вид проката имеет более высокое качество по сравнению с предыдущим, за счет меньшей кривизны и лучшими характеристиками по работе на изгиб и растяжение. Естественно и цена на этот уголок выше.
Далее уголки можно разделить по длине, которые выпускаются они таких видов:
- мерной длины;
- мерной длины кратного размера;
- немерной, то есть длины в соответствии с заказом;
- длиной, имеющей ограничения в пределах немерной длины.

По качеству продукция делится на продукцию А и В, где А – продукция высокого качества, В – продукция обычного качества.
Стандарты, которые определяют тип и вид уголка, а также его материалНа уголки существуют ГОСТы, ТУ.
На сегодняшний день действуют такие стандарты:
Действующие стандарты
| Номер | Название |
| ДСТУ 2251-93 ГОСТ 8509-93) | Уголки стальные горячекатаные равнополочные. Сортамент |
| ISO 657-1:1989 Е | Уголки равнополочные. Размеры |
| ДСТУ ISO 657.2-2001 | Профили стальные горячекатаные. Часть 2. Уголки неравнополочные. Размеры> |
| ГОСТ 8510-86 | Уголки стальные горячекатаные неравнополочные. Сортамент |
| ДСТУ 2254-93 (ГОСТ 19771-93) | Уголки стальные гнутые равнополочные. Сортамент |
| ДСТУ 2255-93 (ГОСТ 19772-93) | Уголки стальные гнутые неравнополочные. Сортамент Сортамент |
Например, уголок неравнополочный должен быть изготовлен по ГОСТ 8510-86, ГОСТ 19772-93, в которых предполагается материал для изготовления – углеродистая сталь.
При изготовлении уголка того или другого вида используют углеродистую конструкционную сталь разного вида. Это сталь углеродистая качественная, например, 05кп, 08пс, 08Фкп, обыкновенного качества, например ВСт 2кп,ВСт5пс и сталь низколегированная, например, 08Г2Д, 09Г2. Также могут применяться и другие виды стали, которые указаны в ГОСТ 380-94.
Уголок считается наиболее применяемым из выпускаемого проката, так как он очень хорошо сваривается в различные конструкции, форма его достаточно удобная, он выдерживает практически все нагрузки, кроме нагрузки на скручивание.
Очень широко уголок применяется в строительстве – от создания различный металлоконструкций, как для высоких нагрузок, так и для создания дополнительных элементов. Его применяют в арках мостов, перекрытий, для оконных и дверных проемов и так далее, в зависимости от размеров проката.
Его применяют в арках мостов, перекрытий, для оконных и дверных проемов и так далее, в зависимости от размеров проката.
Применяется уголок и машиностроительной промышленности, например, в качестве каркасов и станин, в производстве судов и другой техники. В зависимости от нагрузки, выбирают нужное качество профиля.
Большое применение малоразмерного уголка нашло в мебельной промышленности. Немалый процент потребления уголка и для индивидуального пользования, например для строительства индивидуальных домов, гаражей, теплиц, заборов.
Для строительства чаще применяется уголок, изготовленный из нержавеющей стали, например, для изготовления каркаса здания, который затем закладывается или заливается бетоном для постройки монолитного дома. Может применяться профиль, покрытый цинком. Применение уголка может быть в самых различных областях, тем более материал, из которого он может быть изготовлен, достаточно разнообразен, как и размеры.
Производители уголкаВ настоящее время используется металлопрокат, который изготавливается в России, это примерно 62%, Белоруссии и Казахстане, это примерно 25%, 8% Китай, остальные 5% это страны зарубежья, например, Италия, Германия, Украина, Испания, Англия,Турция
Российских компаний, которые выпускают прокат, можно назвать около 20 предприятий, которые, в основном находятся в месте добычи железной руды, например, Алчевский металлургический комбинат, Омский металлокомбинат, Челябинский, «ГУП» г. Ангарск. Алюминиевый уголок выпускает холдинг РУСАЛ.
Ангарск. Алюминиевый уголок выпускает холдинг РУСАЛ.
Если возникла потребность покупки уголка, необходимый вес, размер можно рассчитать вручную, используя данные из таблицы. Что бы сделать заказ на металлобазе, нужно точно дать им расчет того, что вам нужно, что бы не переплачивать за остатки.
Нужно просто взять вес метрового отрезка уголка, который нужен, перемножить его на всю длину, которая вам нужна. Если нужно несколько видов уголка, придется помучиться.
Но можно просто воспользоваться электронным онлайн калькулятором, который мы предлагаем на нашем сайте бесплатно. Все формулы в нём уже заложены. По таблице выбираем данные – вид уголка, размеры полок, угол округления и остальное.
Заносите данные в таблицу и сразу получаете готовый результат, причем при помощи этого калькулятора можете получить данные о самых распространённых размерах уголка.
ГОСТ 8509-93. Уголки стальные горячекатаные, равнополочные
Масса 1 погонного метра уголка по ГОСТ 8509-93
| Обозначение профиля | Размер полки (A), мм | Толщина стенки (s), мм | Вес 1 метра погонного, кг | Метров уголка в тонне |
|---|---|---|---|---|
| Уголок 20×3 | 20 | 3 | 0. 89 89 | 1123.6 |
| Уголок 20×4 | 20 | 4 | 1.15 | 869.6 |
| Уголок 25×3 | 25 | 3 | 1.12 | 892.9 |
| Уголок 25×4 | 25 | 4 | 1.46 | 684.9 |
| Уголок 25×5 | 25 | 5 | 1.78 | 561.8 |
| Уголок 28×3 | 28 | 3 | 1.27 | 787.4 |
| Уголок 30×3 | 30 | 3 | 1.36 | 735.3 |
| Уголок 30×4 | 30 | 4 | 1.78 | 561.8 |
| Уголок 30×5 | 30 | 5 | 2.18 | 458.7 |
| Уголок 32×3 | 32 | 3 | 1.46 | 684.9 |
| Уголок 32×4 | 32 | 4 | 1.91 | 523.6 |
| Уголок 35×3 | 35 | 3 | 1.6 | 625 |
| Уголок 35×4 | 35 | 4 | 2.1 | 476.2 |
| Уголок 35×5 | 35 | 5 | 2. 58 58 | 387.6 |
| Уголок 40×3 | 40 | 3 | 1.85 | 540.5 |
| Уголок 40×4 | 40 | 4 | 2.42 | 413.2 |
| Уголок 40×5 | 40 | 5 | 2.98 | 335.6 |
| Уголок 40×6 | 40 | 6 | 3.52 | 284.1 |
| Уголок 45×3 | 45 | 3 | 2.08 | 480.8 |
| Уголок 45×4 | 45 | 4 | 2.73 | 366.3 |
| Уголок 45×5 | 45 | 5 | 3.37 | 296.7 |
| Уголок 45×6 | 45 | 6 | 3.99 | 250.6 |
| Уголок 50×3 | 50 | 3 | 2.32 | 431 |
| Уголок 50×4 | 50 | 4 | 3.05 | 327.9 |
| Уголок 50×5 | 50 | 5 | 3.77 | 265.3 |
| Уголок 50×6 | 50 | 6 | 4.47 | 223.7 |
| Уголок 50×7 | 50 | 7 | 5. 15 15 | 194.2 |
| Уголок 50×8 | 50 | 8 | 5.82 | 171.8 |
| Уголок 56×4 | 56 | 4 | 3.44 | 290.7 |
| Уголок 56×5 | 56 | 5 | 4.25 | 235.3 |
| Уголок 60×4 | 60 | 4 | 3.71 | 269.5 |
| Уголок 60×5 | 60 | 5 | 4.58 | 218.3 |
| Уголок 60×6 | 60 | 6 | 5.43 | 184.2 |
| Уголок 60×8 | 60 | 8 | 7.1 | 140.9 |
| Уголок 60×0 | 60 | 10 | 8.7 | 114.9 |
| Уголок 63×4 | 63 | 4 | 3.9 | 256.4 |
| Уголок 63×5 | 63 | 5 | 4.81 | 207.9 |
| Уголок 63×6 | 63 | 6 | 5.72 | 174.8 |
| Уголок 65×6 | 65 | 6 | 5.91 | 169.2 |
| Уголок 65×8 | 65 | 8 | 7. 73 73 | 129.4 |
| Уголок 70×4 | 70 | 4.5 | 4.87 | 205.3 |
| Уголок 70×5 | 70 | 5 | 5.38 | 185.9 |
| Уголок 70×6 | 70 | 6 | 6.39 | 156.5 |
| Уголок 70×7 | 70 | 7 | 7.39 | 135.3 |
| Уголок 70×8 | 70 | 8 | 8.37 | 119.5 |
| Уголок 70×0 | 70 | 10 | 10.29 | 97.2 |
| Уголок 75×5 | 75 | 5 | 5.8 | 172.4 |
| Уголок 75×6 | 75 | 6 | 6.89 | 145.1 |
| Уголок 75×7 | 75 | 7 | 7.96 | 125.6 |
| Уголок 75×8 | 75 | 8 | 9.02 | 110.9 |
| Уголок 75×9 | 75 | 9 | 10.07 | 99.3 |
| Уголок 80×5 | 80 | 5.5 | 6.78 | 147.5 |
| Уголок 80×6 | 80 | 6 | 7. 36 36 | 135.9 |
| Уголок 80×7 | 80 | 7 | 8.51 | 117.5 |
| Уголок 80×8 | 80 | 8 | 9.65 | 103.6 |
| Уголок 80×10 | 80 | 10 | 11.88 | 84.2 |
| Уголок 80×12 | 80 | 12 | 14.05 | 71.2 |
| Уголок 90×6 | 90 | 6 | 8.33 | 120.1 |
| Уголок 90×7 | 90 | 7 | 9.64 | 103.7 |
| Уголок 90×8 | 90 | 8 | 10.93 | 91.5 |
| Уголок 90×9 | 90 | 9 | 12.2 | 82 |
| Уголок 90×10 | 90 | 10 | 13.48 | 74.2 |
| Уголок 90×12 | 90 | 12 | 15.96 | 62.7 |
| Уголок 100×6,5 | 100 | 6.5 | 10.06 | 99.4 |
| Уголок 100×7 | 100 | 7 | 10.79 | 92.7 |
| Уголок 100×8 | 100 | 8 | 12. 25 25 | 81.6 |
| Уголок 100×10 | 100 | 10 | 15.1 | 66.2 |
| Уголок 100×12 | 100 | 12 | 17.9 | 55.9 |
| Уголок 100×14 | 100 | 14 | 20.63 | 48.5 |
| Уголок 100×15 | 100 | 15 | 21.97 | 45.5 |
| Уголок 100×16 | 100 | 16 | 23.3 | 42.9 |
| Уголок 110×7 | 110 | 7 | 11.89 | 84.1 |
| Уголок 110×8 | 110 | 8 | 13.5 | 74.1 |
| Уголок 120×8 | 120 | 8 | 14.76 | 67.8 |
| Уголок 120×10 | 120 | 10 | 18.24 | 54.8 |
| Уголок 120×12 | 120 | 12 | 21.67 | 46.2 |
| Уголок 120×15 | 120 | 15 | 26.68 | 37.5 |
| Уголок 125×8 | 125 | 8 | 15.46 | 64.7 |
| Уголок 125×9 | 125 | 9 | 17. 3 3 | 57.8 |
| Уголок 125×10 | 125 | 10 | 19.1 | 52.4 |
| Уголок 125×12 | 125 | 12 | 22.68 | 44.1 |
| Уголок 125×14 | 125 | 14 | 26.2 | 38.2 |
| Уголок 125×16 | 125 | 16 | 29.65 | 33.7 |
| Уголок 140×9 | 140 | 9 | 19.41 | 51.5 |
| Уголок 140×10 | 140 | 10 | 21.45 | 46.6 |
| Уголок 140×12 | 140 | 12 | 25.5 | 39.2 |
| Уголок 150×10 | 150 | 10 | 23.02 | 43.4 |
| Уголок 150×12 | 150 | 12 | 27.39 | 36.5 |
| Уголок 150×15 | 150 | 15 | 33.82 | 29.6 |
| Уголок 150×18 | 150 | 18 | 40.11 | 24.9 |
| Уголок 160×10 | 160 | 10 | 24.67 | 40.5 |
| Уголок 160×11 | 160 | 11 | 27. 02 02 | 37 |
| Уголок 160×12 | 160 | 12 | 28.35 | 35.3 |
| Уголок 160×14 | 160 | 14 | 33.97 | 29.4 |
| Уголок 160×16 | 160 | 16 | 38.52 | 26 |
| Уголок 160×18 | 160 | 18 | 43.01 | 23.3 |
| Уголок 160×20 | 160 | 20 | 47.44 | 21.1 |
| Уголок 180×11 | 180 | 11 | 30.47 | 32.8 |
| Уголок 180×12 | 180 | 12 | 33.12 | 30.2 |
| Уголок 180×15 | 180 | 15 | 40.96 | 24.4 |
| Уголок 180×18 | 180 | 18 | 48.66 | 20.6 |
| Уголок 180×20 | 180 | 20 | 53.72 | 18.6 |
| Уголок 200×12 | 200 | 12 | 36.97 | 27.1 |
| Уголок 200×13 | 200 | 13 | 39.92 | 25.1 |
| Уголок 200×14 | 200 | 14 | 42. 8 8 | 23.4 |
| Уголок 200×16 | 200 | 16 | 48.65 | 20.6 |
| Уголок 200×18 | 200 | 18 | 54.4 | 18.4 |
| Уголок 200×20 | 200 | 20 | 60.08 | 16.6 |
| Уголок 200×24 | 200 | 24 | 71.26 | 14 |
| Уголок 200×25 | 200 | 25 | 74.02 | 13.5 |
| Уголок 200×30 | 200 | 30 | 87.56 | 11.4 |
| Уголок 220×14 | 220 | 14 | 47.4 | 21.1 |
| Уголок 220×16 | 220 | 16 | 53.83 | 18.6 |
| Уголок 250×16 | 250 | 16 | 61.55 | 16.3 |
| Уголок 250×18 | 250 | 18 | 68.86 | 14.5 |
| Уголок 250×20 | 250 | 20 | 76.11 | 13.1 |
| Уголок 250×22 | 250 | 22 | 83.31 | 12 |
| Уголок 250×25 | 250 | 25 | 93. 97 97 | 10.6 |
| Уголок 250×28 | 250 | 28 | 104.5 | 9.6 |
| Уголок 250×30 | 250 | 30 | 111.44 | 9 |
| Уголок 250×35 | 250 | 35 | 128.51 | 7.8 |
ГОСТ 8510-86. Уголки стальные горячекатаные неравнополочные
Масса 1 погонного метра уголка по ГОСТ 8510-86
| Обозначение профиля | Размер полки (A), мм | Размер полки (B), мм | Толщина стенки (s), мм | Вес 1 метра погонного, кг | Метров уголка в тонне |
|---|---|---|---|---|---|
| Уголок 25×16×3 | 25 | 16 | 3 | 0.9 | 1098.9 |
| Уголок 30×20×3 | 30 | 20 | 3 | 1.1 | 892.9 |
| Уголок 30×20×4 | 30 | 20 | 4 | 1.5 | 689.7 |
| Уголок 32×20×3 | 32 | 20 | 3 | 1.2 | 854.7 |
| Уголок 32×20×4 | 32 | 20 | 4 | 1.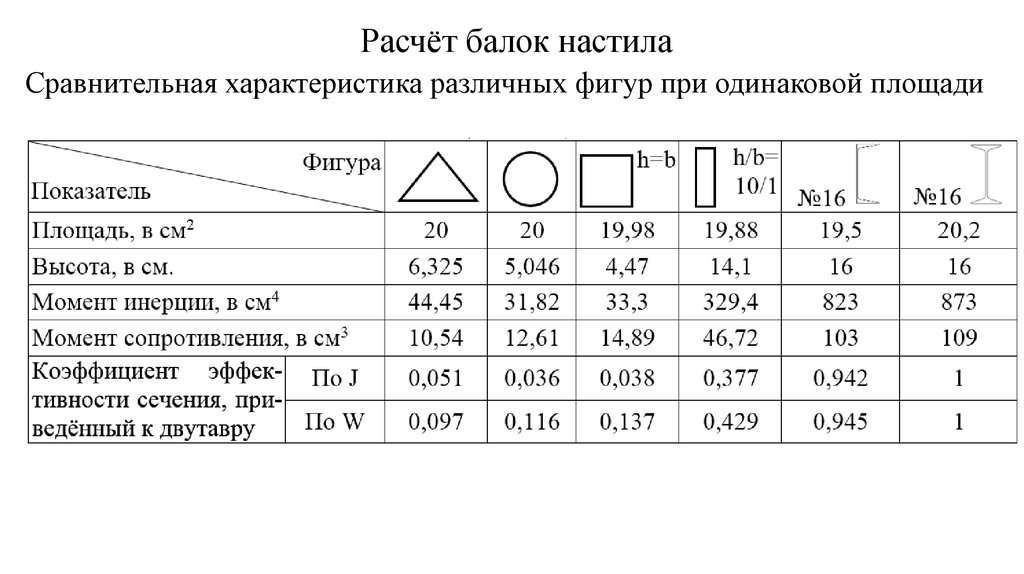 5 5 | 657.9 |
| Уголок 40×25×3 | 40 | 25 | 3 | 1.5 | 675.7 |
| Уголок 40×25×4 | 40 | 25 | 4 | 1.9 | 515.5 |
| Уголок 40×25×5 | 40 | 25 | 5 | 2.4 | 421.9 |
| Уголок 40×30×4 | 40 | 30 | 4 | 2.3 | 442.5 |
| Уголок 40×30×5 | 40 | 30 | 5 | 2.5 | 406.5 |
| Уголок 45×28×3 | 45 | 28 | 3 | 1.7 | 595.2 |
| Уголок 45×28×4 | 45 | 28 | 4 | 2.2 | 454.6 |
| Уголок 50×32×3 | 50 | 32 | 3 | 1.9 | 526.3 |
| Уголок 50×32×4 | 50 | 32 | 4 | 2.4 | 416.7 |
| Уголок 56×36×4 | 56 | 36 | 4 | 2.8 | 355.9 |
| Уголок 56×36×5 | 56 | 36 | 5 | 3.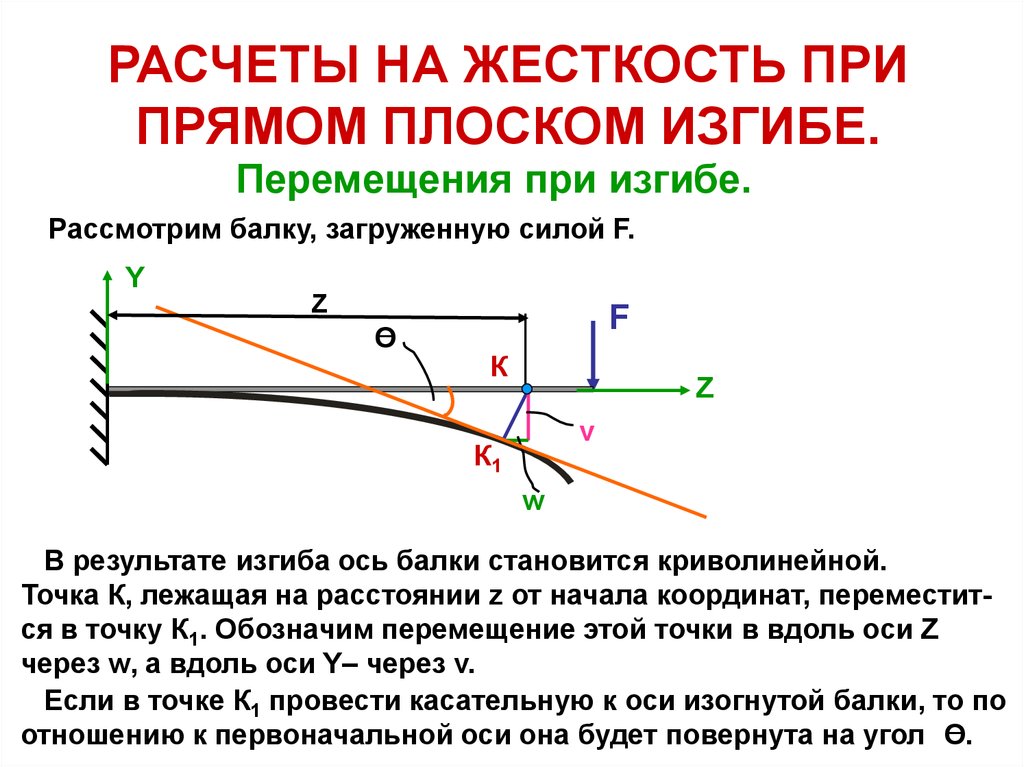 5 5 | 289 |
| Уголок 63×40×4 | 63 | 40 | 4 | 3.2 | 315.5 |
| Уголок 63×40×5 | 63 | 40 | 5 | 3.9 | 255.8 |
| Уголок 63×40×6 | 63 | 40 | 6 | 4.6 | 216 |
| Уголок 63×40×8 | 63 | 40 | 8 | 6 | 165.8 |
| Уголок 65×50×5 | 65 | 50 | 5 | 4.4 | 229.4 |
| Уголок 65×50×6 | 65 | 50 | 6 | 5.2 | 193.1 |
| Уголок 65×50×7 | 65 | 50 | 7 | 5.9 | 168.6 |
| Уголок 65×50×8 | 65 | 50 | 8 | 6.8 | 147.7 |
| Уголок 70×45×5 | 70 | 45 | 5 | 4.3 | 232.6 |
| Уголок 75×60×5 | 75 | 60 | 5 | 4.8 | 208.8 |
| Уголок 75×60×6 | 75 | 60 | 6 | 5.7 | 175. 8 8 |
| Уголок 75×60×7 | 75 | 60 | 7 | 6.6 | 152.2 |
| Уголок 75×60×8 | 75 | 60 | 8 | 7.4 | 134.6 |
| Уголок 80×50×5 | 80 | 50 | 5 | 4.5 | 222.7 |
| Уголок 80×50×6 | 80 | 50 | 6 | 5.9 | 168.9 |
| Уголок 80×60×6 | 80 | 60 | 6 | 6.4 | 156.5 |
| Уголок 80×60×7 | 80 | 60 | 7 | 7.4 | 135.3 |
| Уголок 80×60×8 | 80 | 60 | 8 | 8.4 | 119.5 |
| Уголок 90×56×5 | 90 | 56 | 5.5 | 6.2 | 162.1 |
| Уголок 90×56×6 | 90 | 56 | 6 | 6.7 | 149.3 |
| Уголок 90×56×8 | 90 | 56 | 8 | 8.8 | 114 |
| Уголок 100×63×6 | 100 | 63 | 6 | 7.5 | 132. 8 8 |
| Уголок 100×63×7 | 100 | 63 | 7 | 8.7 | 114.9 |
| Уголок 100×63×8 | 100 | 63 | 8 | 9.9 | 101.3 |
| Уголок 100×63×10 | 100 | 63 | 10 | 12.1 | 82.4 |
| Уголок 100×65×7 | 100 | 65 | 7 | 8.8 | 113.5 |
| Уголок 100×65×8 | 100 | 65 | 8 | 10 | 100.1 |
| Уголок 100×65×10 | 100 | 65 | 10 | 12.3 | 81.3 |
| Уголок 110×70×6 | 110 | 70 | 6.5 | 9 | 111.4 |
| Уголок 110×70×8 | 110 | 70 | 8 | 10.9 | 91.5 |
| Уголок 125×80×7 | 125 | 80 | 7 | 11 | 90.6 |
| Уголок 125×80×8 | 125 | 80 | 8 | 12.6 | 79.5 |
| Уголок 125×80×10 | 125 | 80 | 10 | 15. 5 5 | 64.6 |
| Уголок 125×80×12 | 125 | 80 | 12 | 18.3 | 54.5 |
| Уголок 140×90×8 | 140 | 90 | 8 | 14.1 | 70.8 |
| Уголок 140×90×10 | 140 | 90 | 10 | 17.5 | 57.3 |
| Уголок 160×100×9 | 160 | 100 | 9 | 18 | 55.7 |
| Уголок 160×100×10 | 160 | 100 | 10 | 19.9 | 50.4 |
| Уголок 160×100×12 | 160 | 100 | 12 | 23.6 | 42.4 |
| Уголок 160×100×14 | 160 | 100 | 14 | 27.3 | 36.7 |
| Уголок 180×110×10 | 180 | 110 | 10 | 22.2 | 45.1 |
| Уголок 180×110×12 | 180 | 110 | 12 | 26.4 | 37.9 |
| Уголок 200×125×11 | 200 | 125 | 11 | 27.4 | 36.5 |
| Уголок 200×125×12 | 200 | 125 | 12 | 29. 7 7 | 33.6 |
| Уголок 200×125×14 | 200 | 125 | 14 | 34.4 | 29 |
| Уголок 200×125×16 | 200 | 125 | 16 | 39.1 | 25.6 |
ГОСТ 19771-93. Уголки стальные гнутые равнополочные
Масса 1 погонного метра уголка по ГОСТ 19771-93
| Обозначение профиля | Размер полки (A), мм | Толщина стенки (s), мм | Вес 1 метра погонного, кг | Метров уголка в тонне |
|---|---|---|---|---|
| Уголок 36×3 | 36 | 3 | 1.57 | 636.94 |
| Уголок 40×2,5 | 40 | 2.5 | 1.48 | 675.68 |
| Уголок 40×3 | 40 | 3 | 1.76 | 568.18 |
| Уголок 50×3 | 50 | 3 | 2.23 | 448.43 |
| Уголок 50×4 | 50 | 4 | 2.9 | 344.83 |
| Уголок 55×3 | 55 | 3 | 2.43 | 411.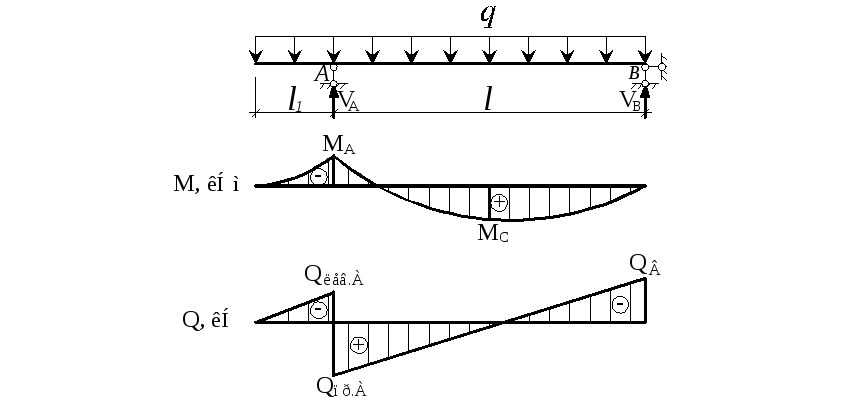 52 52 |
| Уголок 60×3 | 60 | 3 | 2.7 | 370.37 |
| Уголок 60×4 | 70 | 4 | 3.53 | 283.29 |
| Уголок 60×3 | 60 | 3 | 2.67 | 374.53 |
| Уголок 70×4 | 70 | 4 | 4.16 | 240.38 |
| Уголок 80×3 | 80 | 3 | 3.64 | 274.73 |
| Уголок 80×4 | 80 | 4 | 4.79 | 208.77 |
| Уголок 80×5 | 80 | 5 | 5.92 | 168.92 |
| Уголок 80×6 | 80 | 6 | 7.01 | 142.65 |
| Уголок 80×7 | 80 | 7 | 8.11 | 123.3 |
| Уголок 100×4 | 100 | 4 | 6.05 | 165.29 |
| Уголок 100×5 | 100 | 5 | 7.49 | 133.51 |
| Уголок 100×6 | 100 | 6 | 8.89 | 112.49 |
| Уголок 100×7 | 100 | 7 | 10. 31 31 | 96.99 |
| Уголок 120×5 | 120 | 5 | 9.06 | 110.38 |
| Уголок 120×6 | 120 | 6 | 10.78 | 92.76 |
| Уголок 160×4 | 160 | 4 | 9.76 | 102.46 |
ГОСТ 19772-93. Уголки стальные гнутые неравнополочные
Масса 1 погонного метра уголка по ГОСТ 19772-93
| Обозначение профиля | Размер полки (A), мм | Размер полки (B), мм | Толщина стенки (s), мм | Вес 1 метра погонного, кг | Метров уголка в тонне |
|---|---|---|---|---|---|
| Уголок 32x25x2 | 32 | 25 | 2 | 0.84 | 1190.48 |
| Уголок 32x25x2,5 | 32 | 25 | 2.5 | 1.03 | 970.87 |
| Уголок 40x25x2,5 | 40 | 25 | 2.5 | 1.16 | 862.07 |
| Уголок 50x35x3,2 | 50 | 35 | 3.2 | 1.98 | 505. 05 05 |
| Уголок 60x40x3 | 60 | 40 | 3 | 2.23 | 448.43 |
| Уголок 70x50x4 | 70 | 50 | 4 | 3.53 | 283.29 |
| Уголок 80x63x4 | 80 | 63 | 4 | 4.26 | 234.74 |
| Уголок 85x35x4 | 85 | 35 | 4 | 3.53 | 283.29 |
| Уголок 85x67x4 | 85 | 67 | 4 | 4.49 | 222.72 |
| Уголок 90x70x4 | 90 | 70 | 4 | 4.79 | 208.77 |
| Уголок 100x65x4 | 100 | 65 | 4 | 4.95 | 202.02 |
| Уголок 105x100x3 | 105 | 100 | 3 | 4.69 | 213.22 |
| Уголок 110x90x5 | 110 | 90 | 5 | 7.44 | 134.41 |
| Уголок 115x65x5 | 115 | 65 | 5 | 6.71 | 149.03 |
| Уголок 120x100x8 | 120 | 100 | 8 | 12.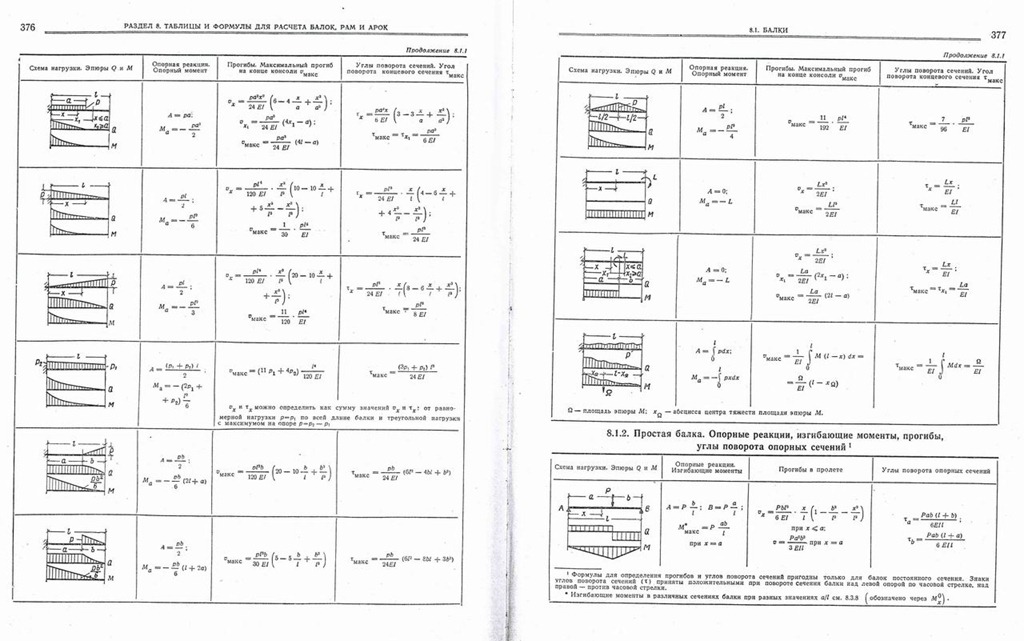 88 88 | 77.64 |
| Уголок 147x125x8 | 147 | 125 | 8 | 15.93 | 62.77 |
| Уголок 152x100x5,5 | 152 | 100 | 5.5 | 10.37 | 96.43 |
| Уголок 155x100x6 | 155 | 100 | 6 | 11.38 | 87.87 |
| Уголок 180x140x6 | 180 | 140 | 6 | 14.55 | 68.73 |
Программа для расчета деревянных балок перекрытия, несущая способность бруса
«Балкомплект» предлагает современные, высокотехнологичные и качественные материалы для малоэтажного домостроения – деревянные двутавровые балки из LVL бруса Ultralam и всевозможные виды крепежа от крупнейшего европейского производителя Rotoblaas, для реализации практически любых задумок и проектов.
Для того, чтобы правильно рассчитать какой тип балки необходимо использовать в каждом конкретном случае и как правильно спроектировать крепежное соединение, требуется провести предварительные расчеты. Партнеры компании «Балкомплект» разработали специальные программы для таких расчетов, доступные для скачивания по ссылкам.
Партнеры компании «Балкомплект» разработали специальные программы для таких расчетов, доступные для скачивания по ссылкам.
Балкомплект-балка 1.0.2 – программа позволяет проверить балку по максимальному изгибающему моменту, по максимальной поперечной силе, по прогибам, на возможность бокового выгиба. При помощи этой программы возможно произвести расчет учитывая любое количество пролетов, различные условия опирания концов балки, произвольный наклон балки, необходимые отверстия. Также существует возможность применения шаблонов для быстрого расчета, редактирования сортамента сечений. В результате обработки данных программа выдает подробный отчет, который может быть использован в качестве рекомендации к выбору той или иной балки. Все системы расчета основаны на существующих стандартах проектирования и расчета деревянных и клееных конструкций.
Ультралам-балка 2.0.2 – проверка по прогибам, устойчивости плоской формы деформирования, по максимальной поперечной силе, по изгибающему моменту. При правильно проведенных расчетах достигается оптимальная прочность и жесткость балки. В результате обработки данных программа выдает подробный отчет, который может быть использован в качестве рекомендации к выбору той или иной балки. Все системы расчета основаны на существующих стандартах проектирования и расчета деревянных и клееных конструкций.
При правильно проведенных расчетах достигается оптимальная прочность и жесткость балки. В результате обработки данных программа выдает подробный отчет, который может быть использован в качестве рекомендации к выбору той или иной балки. Все системы расчета основаны на существующих стандартах проектирования и расчета деревянных и клееных конструкций.
Myproject 3.0 – идеальный помощник от компании Rotoblaas при проектировании различных видов крепежных соединений – соединение на срез шурупами HBS, соединение потайными скобами ALU, постоянное крепление изоляции шурупами DGZ, усиление конструкций шурупами с полной резьбой, соединение между основной и вспомогательной балкой, соединение шпильками-саморезами. Возможен расчет различных конфигураций путем варьирования количества и типов крепежа, изменения наклона, размеров и видов используемого материала, для того чтобы повысить механическую прочность. Скачать руководство пользователя программы Myproject 3.0 можно здесь.
В целях установки балочных перекрытий используется опора – особый тип крепежа. Он фиксируется к двум основам сразу, поэтому нормально выдерживает внушительный вес. Типы, которые можно встретить в продаже – открытый и закрытый. Открытые встречаются чаще, используются в ходе создания соединительных узловых элементов стропил, подстропил в деревянных постройках разного назначения. Несущая способность опоры бруса должна быть рассчитана правильно до начала проведения работ, поскольку от этого зависит надежность и долговечность готового решения. О том, как производятся расчеты, какие особенности имеют рассматриваемые конструкции, мы расскажем далее. Обратите внимание, что есть два способа узнать интересующие данные – теоретический (формульный) и практический.
Он фиксируется к двум основам сразу, поэтому нормально выдерживает внушительный вес. Типы, которые можно встретить в продаже – открытый и закрытый. Открытые встречаются чаще, используются в ходе создания соединительных узловых элементов стропил, подстропил в деревянных постройках разного назначения. Несущая способность опоры бруса должна быть рассчитана правильно до начала проведения работ, поскольку от этого зависит надежность и долговечность готового решения. О том, как производятся расчеты, какие особенности имеют рассматриваемые конструкции, мы расскажем далее. Обратите внимание, что есть два способа узнать интересующие данные – теоретический (формульный) и практический.
Содержание
- Конструкции: особенности
- Почему важно знать несущую способность
- Особенности расчетов:
- Принципы проведения расчетов
- Расчет балки – Пример
- Длина балки
- Определение расчетной нагрузки
- Максимальный изгибающий момент
- Требуемый момент сопротивления
- Момент сопротивления балки перекрытия
- Расчет балки на прочность
- Расчет балки на прогиб (изгиб)
- Конечные параметры балки
- Методика расчета балок перекрытия из клееного бруса и отесанного бревна
Конструкции: особенности
Опоры открытого типа не требуют врезки в деревянное основание, что существенно увеличивает их жесткость. Закрытые предполагают врезку, выглядят более эстетично, поэтому задействуются в открытых местах, где важны привлекательные визуальные качества. Выбор делается на основании ширины основы – это не трудно, поскольку в продаже представлены разные варианты. Крепеж позволяет фиксировать балки на поверхностях из бетона, дерева.
Закрытые предполагают врезку, выглядят более эстетично, поэтому задействуются в открытых местах, где важны привлекательные визуальные качества. Выбор делается на основании ширины основы – это не трудно, поскольку в продаже представлены разные варианты. Крепеж позволяет фиксировать балки на поверхностях из бетона, дерева.
Для удобного крепления в раскрытом виде к поверхностям из дерева производители предусматривают отверстия около 5 мм в диаметре. С учетом технической прочности для фиксации рекомендуется применять шурупы, гвозди с рифлеными поверхностями. Диаметр отверстий составляет 9 либо 11 мм. В качестве крепежей применяются анкеры, шурупы, обычные гвозди. Соединение, которое получится в итоге, будет надежным и долговечным.
Раскрытые опоры брусьев получают путем холодной штамповки с применением стали – оптимального с точки зрения технических характеристик, стоимости материала. Марки, используемые для изготовления крепежей – 08пс, 08Ю. Готовые изделия получаются прочными, имеют высокие характеристики несущей способности. Для увеличения рабочего ресурса раскрытых опор сталь цинкуют – покрытие защищает от коррозии, других негативных внешних воздействий. Цинкование делается горячим способом с применением белого цинка, в который вводятся включения свинца и алюминия. Покрытие предотвращает негативные внешние атмосферные воздействия, обеспечивает изделию привлекательные эстетические характеристики.
Для увеличения рабочего ресурса раскрытых опор сталь цинкуют – покрытие защищает от коррозии, других негативных внешних воздействий. Цинкование делается горячим способом с применением белого цинка, в который вводятся включения свинца и алюминия. Покрытие предотвращает негативные внешние атмосферные воздействия, обеспечивает изделию привлекательные эстетические характеристики.
За счет наличия на лепестках разноразмерных отверстий крепление получается максимально универсальным, простым и удобным в применении. Выбор метизов нужно делать с учетом оказываемого давления на брус, который устанавливается, его прочности. Габариты опорных частей тоже нужно учитывать – они подходят для крепления малых и больших изделий. Если фиксация осуществляется под острым углом, удобно будет использовать сделанные под различными углами крепежные углы, пластины. Некоторые варианты идут с дополнительными ребрами жесткости.
Почему важно знать несущую способность
Под рассматриваемым понятием подразумевается максимально допустимое рабочее давление, которое могут переносить перекрытия, балки, стены, сваи, фундаменты зданий. Выдерживать не просто, а, не утрачивая функциональности, не деформируясь. Если превысить максимальные цифры, конструкция начнет разрушаться.
Выдерживать не просто, а, не утрачивая функциональности, не деформируясь. Если превысить максимальные цифры, конструкция начнет разрушаться.
В ходе проектирования зданий нагрузки измеряются отдельно для всех элементов будущей постройки, почв, где планируется строительство.
Особенности расчетов:
- Почвы – предельно допустимые показатели, на которые рассчитаны почвы. Сопротивление зависит от плотности, уровня влажности, других показателей. Например, чем более плотной является почва, тем ниже в ней содержание воздуха, и выше получится стойкость к деформациям. Сильная влажность, напротив, уменьшает рассматриваемый показатель – исключение составляют не пучинистые грунты с щебнем, песком.
- Свай – в данном случае рассчитываются предельные цифры, которые может «тянуть» уже забитая в грунт свая. Способы подсчетов – теоретические, пробные статистические, зондирование специальными датчиками, динамические нагрузки. Как и для грунта, для свай определенные требования к расчетам прописаны в СНиП.

- Для фундамента – параметр определяет максимум, выдерживаемый основанием дома без деформации и разрушений. Учтите, что после завершения строительных работ дому потребуется время на усадку – сжатие и трамбовку под собственным весом. Итоговый результат для зданий зависит от конструктивных особенностей конкретного объекта, массы стройматериалов, погоды, модели кровли, ее вида, климатических условий. Берутся во внимание давление ветра, общий вес постройки, масса снегового настила (с учетом климатических условий конкретного региона).
Принципы проведения расчетов
Просчеты выполняйте до начала строительства. Важно учитывать величину прогиба в ходе вычислений. Проводите математический анализ полного набора данных – иначе вы просто не сможете построить дом, либо пострадают его эксплуатационные характеристики. Замерьте пролет, который предстоит перекрыть балками, правильно выберите тип, метод крепления. Важно рассчитать, как глубоко фиксаторы будут входить в стену. Только когда вы определитесь с данными параметрами, можно выполнять остальные вычисления.
Только когда вы определитесь с данными параметрами, можно выполнять остальные вычисления.
Для каждой деревянной доски нужно измерить длину – она равна пролету. Если вы планируете стеновую заделку, этот момент также учитывается. Многое решает сырье, используемое в ходе строительства – в кирпич делается загонка в гнезда на 10 см или больше, для дерева будет достаточно 7 см. Длина бревен/досок при использовании в процессе монтажа кронштейнов, хомутных элементов будет равняться проему. То есть вам нужно замерить удаление одной стены от второй, а потом рассчитать предельно допустимые значения. При формировании кровельного ската бревна выносят за стены на 40 см (плюс-минус). Есть ограничения по максимальным значениям – для обрезных это не более 6 м, иначе возрастет прогиб, и упадет стойкость. Если пролет больше, используется не обычный, а клееный материал.
В малоэтажном строительстве используются в основном однопролетные балочные изделия, которые могут иметь вид брусьев, досок, бревен. Протяженность элементов тоже варьируется в широком диапазоне, определяется она с учетом технических параметров возводимого здания. На строительных сайтах встречаются онлайн-калькуляторы, которыми удобно пользоваться для ввода данных и быстрых подсчетов.
Протяженность элементов тоже варьируется в широком диапазоне, определяется она с учетом технических параметров возводимого здания. На строительных сайтах встречаются онлайн-калькуляторы, которыми удобно пользоваться для ввода данных и быстрых подсчетов.
Оптимальным при анализе балочных перекрытий в плане оказываемого давления считается диапазон 2.4-4 м. Площадь с пропорциональным соотношением параметров высоты и ширины 1.5:1 является оптимальным сечением. Изгиб делится на сопротивляющий момент, полученное в итоге значение должно быть ниже номинальной несущей способности. Внимательно сверяйте все данные, чтобы не допускать ошибок.
Не забывайте учитывать прогиб, материал изготовления, способ обработки. Первый показатель оказывает непосредственное влияние на прочность конструкции, если он сильный, страдает внешний вид перекрытия, если очень сильный – появляются риски аварий. Чтобы узнать прогиб, предельные нагрузочные величины для доски умножайте на длину балок и на 2, а потом полученный множитель делите на 8.
Если в своем будущем доме Вы планируете устройство деревянного междуэтажного и чердачного перекрытия, то Вам необходимо знать расстояние между балками и их оптимальное сечение. А для этого делается специальный расчет. Без него Вы рискуете оказаться на нижележащем этаже или потратить на закупку материалов лишние деньги.
1. Калькулятор
2. Инструкция к калькулятору
Конечно, расчет деревянных балок — это достаточно нудное и долгое занятие. Поэтому для ускорения процесса и для быстрой проработки сразу нескольких вариантов был создан данный калькулятор. С его помощью можно проверить несущую способность (расчет по прочности — I группа предельных состояний) и жесткость (расчет по прогибу — II группа предельных состояний) следующих балок:
- Тип 1 — цельная деревянная балка.
- Тип 2 — клееная балка из досок.
- Тип 3 — клееная балка из шпона LVL.
- Тип 4 — обрезанное бревно.
Рассчитывается балка на изгиб, как шарнирно опертая с равномерно-распределенной нагрузкой, в соответствии со СНиП II-25-80 (СП 64. 13330.2011) «Деревянные конструкции» , который можно скачать . Для удобства некоторые таблицы необходимые для расчета вынесены в отдельную статью .
13330.2011) «Деревянные конструкции» , который можно скачать . Для удобства некоторые таблицы необходимые для расчета вынесены в отдельную статью .
Кроме выше перечисленного данный калькулятор способен рассчитать общий объем балок и их стоимость.
Примеры расчета |
- Сбор нагрузок на балки перекрытия онлайн.
- Расчет прямоугольной трубы
- Расчет квадратной трубы
- Расчет двутавра
- Расчет швеллера
- Расчет уголка
Условия эксплуатации:
Длина пролета (L) — расстояние между двумя опорами балки. Например, для стен, это расстояние между двумя внутренними гранями этих стен.
Шаг балок (Р) — шаг, с которым предполагается укладывать балки. Обычно он составляет 500-1000 мм.
Вид перекрытия — здесь Вы должны выбрать, какое перекрытие (междуэтажное или чердачное) будет в данный момент рассчитываться. Для справки, чердачное — это перекрытие над последним этажом в случае, если чердак не жилой.
Длина стены (Х) — длина стены, на которую опираются балки с одной стороны.
Срок службы — предполагаемое время до замены балок.
Температура — максимальная температура, при которой будут эксплуатироваться конструкции.
Влажность — расшифровывается так: Эксплуатационная влажность древесины/Максимальная влажность воздуха при температуре 20 °С. Чаще всего, для жилых помещений — это до 12%/до 65%.
Характеристики балки:
Материал — порода древесины, из которой сделана балка.
Длина (А), ширина (В), высота (Н) балки — размеры рассчитываемой балки.
Сорт древесины — из какого сорта древесины выполнена балка.
Пропитка — имеется ввиду глубокая пропитка антипиренами под давлением.
Коэф. mб — коэффициент для балок с высотой сечения более 50 мм. Выбирается по таблице 4 . Если высота сечения балки ниже 50 мм, то ставится цифра 1.
Нагрузка:
Нормативные и расчетные нагрузки — максимальные нагрузки, которые действуют на балки перекрытия.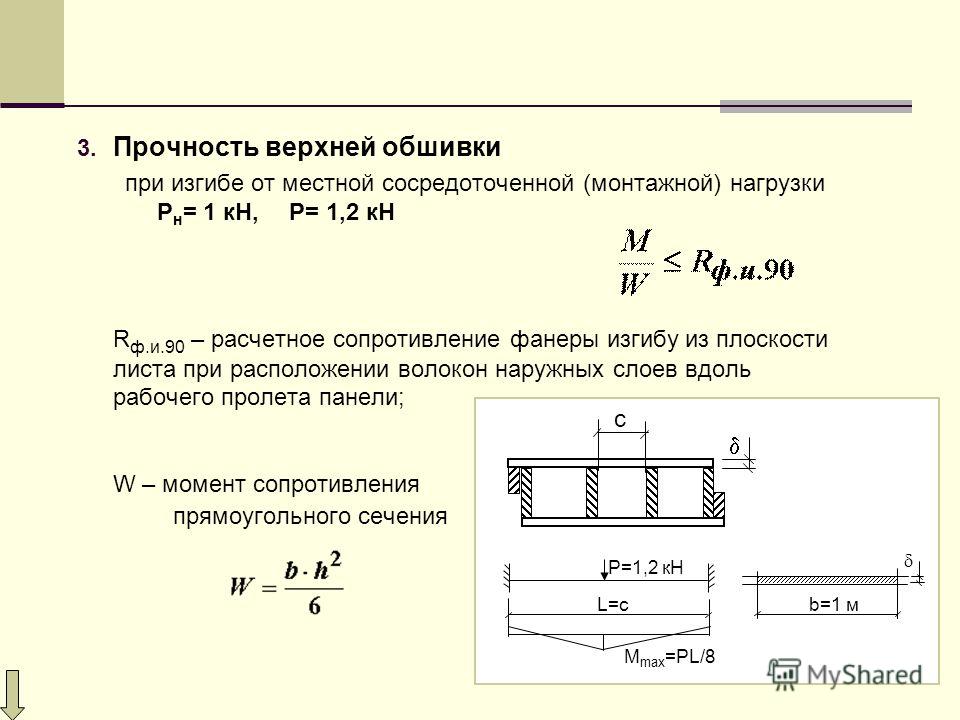 Для сбора нагрузок Вы можете воспользоваться специальным примером.
Для сбора нагрузок Вы можете воспользоваться специальным примером.
Коэф. mд — вводится в случае, если напряжения в элементах, возникающие от постоянных и временных длительных нагрузок, превышают 80% суммарного напряжения от всех нагрузок.
Цена за кубометр — стоимость 1 м3 пиломатериала.
Здесь и в последующих типах будут рассматриваться только новые переменные.
Толщина слоя (Т) — толщина досок, из которых склеивается балка.
Коэф. kw — коэффициент, определяемый по таблице 11 .
Тип балки — рассчитываются балки типа Ultralam (таблица 15 ).
Диаметр балки (D) — диаметр оцилиндрованного бревна, из которого была сделана балка путем его обрезки с одной или двух сторон.
Расчет по прочности:
Wбалки — момент сопротивления рассчитываемой балки.
Wтреб — требуемый момент сопротивления.
Запас — в случае, если Wбалки < Wтреб — в графе показывается отрицательное значение с указанием процента нехватки сечения; в случае, когда Wбалки > Wтреб — значение положительное, указывающее на сколько процентов сечение существующей балки больше требуемого.
Расчет по прогибу:
Fбалки — прогиб рассчитываемой балки заданного сечения.
Fmax — максимальный прогиб из условия жесткости в зависимости от вида перекрытия.
Запас — Fбалки < Fmax — сечение удовлетворяет условию жесткости с запасом, указанным в графе; Fбалки > Fmax — сечение балки не проходит для указанного пролета и шага балок.
Другие параметры:
Количество балок — получаемое количество балок, лежащих вдоль стены длиной X с шагом P.
Общий объем — общая кубатура балок.
Стоимость — количество затраченных средств на покупку данного пиломатериала.
Балка – это элемент строительных несущих конструкций, который широко используется для возведения межэтажных перекрытий. Перекрытия, в свою очередь, предназначены для разделения по высоте смежных помещений, а также принятия статических и динамических нагрузок от находящихся на нем предметов интерьера, оборудования, людей и т.д.
В большинстве случаев, для частного домостроения используются деревянные балки из цельного бруса, отесанного бревна, клееных досок или шпона. Эти материалы, при правильном подборе параметров, способны обеспечить необходимую прочность и жесткость основания, что является залогом долговечности постройки.
Эти материалы, при правильном подборе параметров, способны обеспечить необходимую прочность и жесткость основания, что является залогом долговечности постройки.
Мы предлагаем вам выполнить онлайн расчет балки перекрытия на прочность и изгиб, подобрать её сечение и определить шаг между балками. Также вы получите набор персональных чертежей и 3D-модель для лучшего восприятия возводимой конструкции. Программа учитывает СНиП II-25-80 (СП 64.13330.2011) и другие справочные источники.
Точный и грамотный расчет деревянных балок в сервисе KALK.PRO, позволяет узнать все необходимые параметры для сооружения крепкого перекрытия. Все вычисления бесплатны, есть возможность сохранения рассчитанных данных в формате PDF, плюс доступны схемы и 3D-модель.
Расчет балки – Пример
Алгоритм работы программы для расчета балок основывается на СП 64.13330.2011 (Актуализированная редакция СНиП II-25-80). Для большей наглядности, мы разберем расчет однопролетной балки на прогиб и прочность в примере, кратко описывая основные этапы вычисления и формулы.
Длина балки
Расчетная длина балки определяется значением длины пролета и запасом для укладывания их на стену.
Узнать протяженность между пролетами не составляет трудности – с помощью рулетки замерьте расстояние, которые необходимо перекрыть балками, и к полученному числу добавьте величину заделки в «гнезда» равную 300 мм (по 150 мм на сторону) или более.
В случае, когда вы собираетесь крепить балки на специальные металлические крепления, длина пролета будет равна длине балки.
Если ваше помещение имеет неправильную форму, например, 4х5 м, правильнее будет использовать балки меньшей длины, т.е. 4 м, а не 5 м.
Определение расчетной нагрузки
Для того чтобы правильно рассчитать нагрузку на деревянную балку, нужно определить все виды оказываемых воздействий на перекрытие.
Величину нагрузки можно узнать двумя путями: использовать СНиП 2.01.07-85* Нагрузки и воздействия и с его помощью высчитать все необходимые коэффициенты вручную, а затем сложить их, или же можно взять нормативные данные из справочников.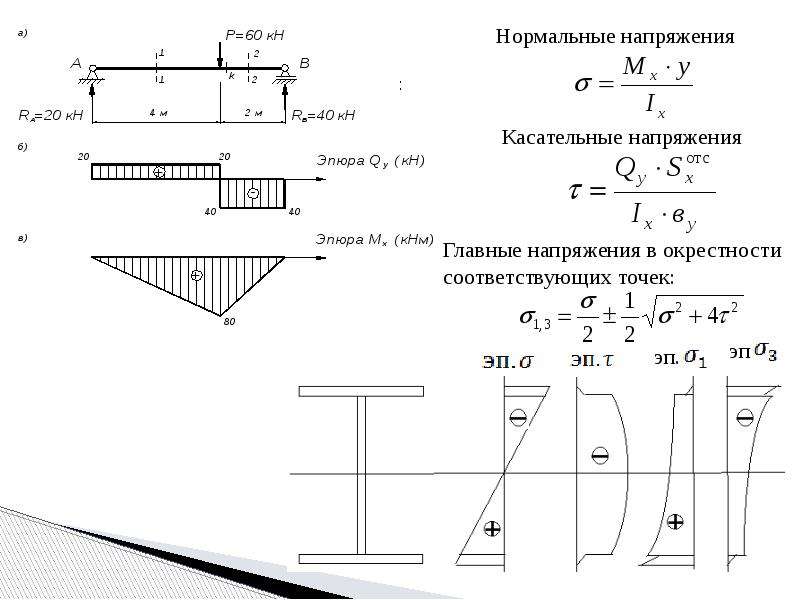 Если вы произведете все расчеты правильно, то первый вариант будет более точен, однако никто не застрахован, что при выполнении долгих громоздких вычислений не будет допущена ошибка.
Если вы произведете все расчеты правильно, то первый вариант будет более точен, однако никто не застрахован, что при выполнении долгих громоздких вычислений не будет допущена ошибка.
Поэтому для получения приблизительного расчета, целесообразнее взять стандартные величины и применять их в последующих формулах. Согласно справочникам, для межэтажных перекрытий расчетная нагрузка обычно составляет 400 кг/м2, а для чердаков – 200 кг/м2.
Типовые нагрузки для межэтажных перекрытий — 400 кг/м2 и чердаков – 200 кг/м2 применимы не во всех ситуациях. Если подразумевается, что на основание будет воздействовать ненормально большой вес, например, от тяжелого оборудования – необходимо произвести корректировку начальных параметров.
Максимальный изгибающий момент
Изгибающий момент – момент внешних сил относительно нейтральной оси сечения балки или другого твёрдого тела, иначе простыми словами, это произведение силы на плечо.
Максимальный изгибающий момент, соответственно, принимает наибольшее значение, которое может выдержать данное тело без нарушения целостности.
Если на балку будет действовать равномерно распределенная нагрузка (в калькуляторе реализован именно этот случай), то значение максимального изгибающего момента будет равно:
Изгибающий момент (формула): Mmax = q × l2 / 8
- q – величина нагрузки на перекрытие;
- l – величина пролета перекрытия.
Требуемый момент сопротивления
Момент сопротивления – это способность материала оказывать сопротивления к изгибу, растяжению или сжатию. Для того чтобы определить это значение для деревянной балки, нужно воспользоваться готовой формулой:
Требуемый момент сопротивления (формула): Wтреб = Мmax / R
- Мmax – величина максимального изгибающего момента;
- R – величина расчетного сопротивления древесины.
Отдельно нужно рассказать о величине R. Она имеет целый ряд поправочных коэффициентов, которые нужно учитывать при расчете балки, если вы хотите получить максимально точный результат. Полная формула выглядит так:
Расчетное сопротивление древесины (формула): R = Rи × mп × mд × mт × ma × γсc × …
- Rи – расчетное сопротивление древесины изгибу, подбираемое в зависимости от расчетных значений для сосны, ели и лиственницы при влажности 12% согласно СП 64.
 13330.2011;
13330.2011; - mп – коэффициент перехода для других пород древесины;
- mд – поправочный коэффициент принимаемый в случае, когда постоянные и временный длительные нагрузки превышают 80% суммарного напряжения от всех нагрузок;
- mт – температурный коэффициент;
- ma – коэффициент принимаемый в случае, когда дерево подвергается пропитке антипиренами;
- γсc – коэффициент срока службы древесины.
- … – существуют другие менее важные коэффициенты, однако при расчетах они практически не используются, так как величина поправки слишком незначительна.
Получается, что по сути, величина R это произведение расчетного сопротивления древесины изгибу и различных поправок. В большинстве случаев для получения ориентировочного результата, эти поправки не учитываются, а значение R принимается равным Rи.
Момент сопротивления балки перекрытия
В зависимости от формы сечения балки (квадрат, прямоугольник, круг, овал…) формулы нахождения фактического момента сопротивления будут отличаться.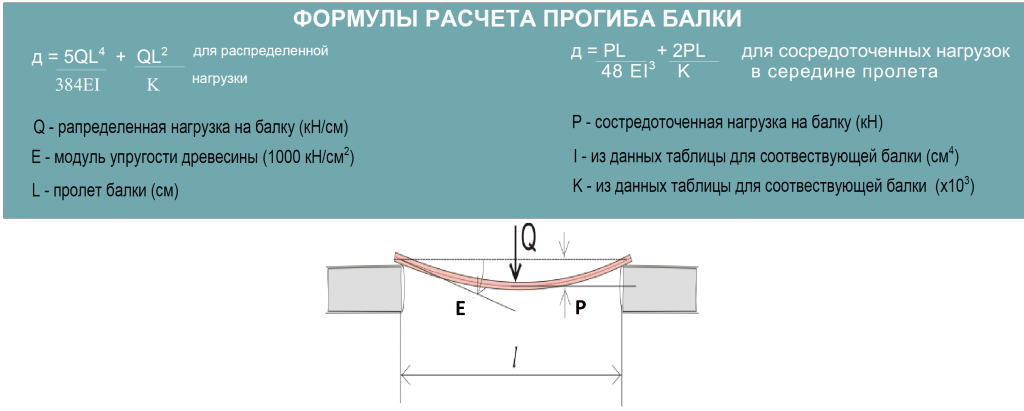 В наших калькуляторах применяются только два типа профиля: прямоугольный и тесаное бревно. Мы продолжим разбирать алгоритм на примере прямоугольного сечения:
В наших калькуляторах применяются только два типа профиля: прямоугольный и тесаное бревно. Мы продолжим разбирать алгоритм на примере прямоугольного сечения:
Момент сопротивления балки (формула): W = b × h3 /6
- b – ширина балки;
- h – высота балки.
Расчет балки на прочность
Для того чтобы определить подходит балка по прочности или нет, нужно чтобы момент сопротивления балки перекрытия (W), равнялся или был больше требуемого момента (Wтреб ):
Wтреб ≤ W
Но вычислить реальный момент сопротивления балки перекрытия мы не можем, так как не известна ее высота. В этом случае нужно или воспользоваться перебором сечений, исходя из условия, что наиболее оптимальное соотношение высоты к ширине 1,4:1, или же просто принять W = Wтреб, в силу того, что мы не нарушаем условий заданной формулы. Также, после этих манипуляций станет известен параметр h.
Онлайн калькулятор KALK.PRO расчета балки на прочность оперативно вычислит нужное сечение, чтобы перекрытие выдержало расчетную нагрузку БЫСТРО и БЕСПЛАТНО.
Расчет балки на прогиб (изгиб)
Методика определения прогиба балки значительно проще. При распределенной нагрузке, применяется формула:
Прогиб балки (формула): f = (5 × q × l4 ) / (384 × E × I)
- q – величина нагрузки на перекрытие;
- l – величина пролета перекрытия;
- E – модуль упругости;
- I – момент инерции.
Первые два параметра нам известны, модуль упругости для древесины обычно принимается равным 100 000 кгс/м², хотя это и не всегда так, а момент инерции, в зависимости от формы сечения, рассчитывается по разным формулам. Для прямоугольника:
Момент инерции (формула): I = b × h4 /12
- b – ширина балки;
- h – высота балки.
Собирая все в кучу, мы получим итоговую формулу расчета прогиба балки:
Прогиб балки (итоговая формула): f = (5 × q × l4 ) / (384 × E × (b × h4 / 12))
После того, как вы получите искомое значение, нужно сравнить его с величиной допустимого (предельного) прогиба балки в долях от пролета. Этот параметр устанавливается СНиП II-25-80 «Деревянные конструкции»:
Этот параметр устанавливается СНиП II-25-80 «Деревянные конструкции»:
Элементы конструкций | Максимальный прогиб балки, не более |
1. Балки междуэтажных перекрытий | |
2. Балки чердачных перекрытий | |
3. Перекрытия при наличии стяжки/штукатурки |
Например, для межэтажных перекрытий при длине пролета равной 400 см мы получим условие – 400/250, т.е. предельно возможный изгиб в данной ситуации 1,6 см.
Если ваше значение f превышает его, необходимо изменять сечение балки в большую сторону, до тех пор, пока оно не станет меньше величины предельного прогиба.
Наш калькулятор прогиба деревянной балки сам подберет нужные параметры сечения и избавит вас от сложных громоздких вычислений.
Конечные параметры балки
После того, как вы подберете сечение при расчете на прочность и прогиб/изгиб, можно будет определить минимально допустимые параметры балки.
Предположим, что при расчете на прочность вы получили сечение – 165х150 мм, а при расчете на прогиб – 239х150 мм. Очевидно, что в подобной ситуации следует выбирать наибольшую величину, то есть значение на прогиб, поскольку если вы сделаете ровно наоборот, перекрытие выдержит нагрузку, но очень сильно деформируется и ни о каком ровном потолке не может быть и речи.
В результате расчета несущей способности деревянной балки, мы используем сечение равное 239х150 мм, но тут сталкиваемся с очередной проблемой – балок такого размера серийно никто не производит. В этом случае нужно производить округление обязательно в большую сторону, обычно кратно 50 мм, т.е. нам подойдет балка 250х150 мм. В некоторых ситуациях, можно обратиться к ГОСТ 24454-06, в нем указаны все типовые размеры материалов.
Расчет балки онлайн без знания сопромата – одно из главных преимуществ сервиса KALK.PRO.
Методика расчета балок перекрытия из клееного бруса и отесанного бревна
Технология расчета балок перекрытия из клееного бруса практически не отличается от изделий из цельной древесины. Все этапы работы с калькулятором совпадают и никакие дополнительные коэффициенты вводить не нужно, но при самостоятельном вычислении в формулу нахождения величины расчетного сопротивления (R), нужно будет добавить дополнительный коэффициент kw , который учитывает форму и размер поперечного сечения.
Все этапы работы с калькулятором совпадают и никакие дополнительные коэффициенты вводить не нужно, но при самостоятельном вычислении в формулу нахождения величины расчетного сопротивления (R), нужно будет добавить дополнительный коэффициент kw , который учитывает форму и размер поперечного сечения.
Например, для прямоугольных клееных балок принимаются следующие поправки:
Также для клееных балок из шпона LVL Ultralam, существует более подробная аннотация с характеристиками на сайте производителя, в которой помимо значений величины R, существует подробные характеристики модуля упругости (E) для каждого вида продукции:
Модуль упругости Е, МПа | ||||
16 000 | 15 600 | 14 000 | 11 000 | 12 700 |
В случае расчета тесаного бревна (лафета), немного изменяются исходные формулы момента сопротивления и момента инерции, так как форма сечения балки отличается от прямоугольной. Помимо этого, есть и отличия в ширине отеса, оно может быть равным половине или трети диаметра, что также приводит к изменению начальных коэффициентов для обеих формул.
Помимо этого, есть и отличия в ширине отеса, оно может быть равным половине или трети диаметра, что также приводит к изменению начальных коэффициентов для обеих формул.
Ширина отеса равна 1/2 диаметра | Ширина отеса равна 1/3 диаметра |
Момент сопротивления | |
W = 0,088D3 | W = 0,09781D3 |
Момент инерции | |
I = 0,039D4 | I = 0,04611D4 |
Расчет балки на прочность, примеры расчетов металлоконструкций на изгиб, жесткости стальных конструкций
Подбор и проверка металлических конструкций в ПК ЛИРА 10.4 имеет ряд преимуществ и особенностей. Разберем подробно тонкости расчёта конструирования металлических конструкций.
В ПК ЛИРА 10.4 реализована функция автоматического определения характера работы элемента. В процессе расчёта производится внутрипрограммный выбор характера работы элементов стальных конструкций (центральное растяжение-сжатие; сжатие-растяжение с изгибом вокруг одной или двух главных осей; изгиб в одном или в двух главных направлениях). Данная функция программы освобождает пользователя от анализа работы элемента и, таким образом, снижает вероятность допущения ошибки, поскольку один и тот же элемент при различных комбинациях загружений может работать по-разному. Выбор производится в зависимости от соотношения действующих в рассматриваемом сечении усилий, которое определяется величиной относительного или приведенного относительного эксцентриситета (таблица 1).
Данная функция программы освобождает пользователя от анализа работы элемента и, таким образом, снижает вероятность допущения ошибки, поскольку один и тот же элемент при различных комбинациях загружений может работать по-разному. Выбор производится в зависимости от соотношения действующих в рассматриваемом сечении усилий, которое определяется величиной относительного или приведенного относительного эксцентриситета (таблица 1).
Таблица 1.
| N < 0 (присутствует сжатие) | N > 0 (присутствует растяжение) | ||
| Приведенный относительный эксцентриситет для сжатой грани mef y(z) | Характер работы относительно рассматриваемой оси | Относительный эксцентриситет для растянутой грани m y(z) | Характер работы относительно рассматриваемой оси |
| Сжатие | Растяжение | ||
| Сжатие с изгибом | Растяжение с изгибом | ||
| Изгиб | Изгиб | ||
В настоящей версии программы выполняются следующие проверки стальных конструкций, в качестве нормативного документа будем рассматривать СП 16. 13330.2011.
13330.2011.
Первое предельное состояние
Прочность
Таблица 2.
| Проверки прочности | Обозначение | Формулы проверок |
| СП 16.13330.2011 | ||
| Прочность по нормальным напряжениям: | (106) – без учёта стеснённого кручения. (105) – без учёта стеснённого кручения. | |
| – без учёта развития пластических деформаций | ||
| – с учётом развития пластических деформаций | ||
| Прочность несимметричных сечений из высокопрочной стали по нормальным напряжениям растяжения | (107) | |
| Прочность по касательным напряжениям | (42) | |
| Прочность по приведенным напряжениям (совместное действие нормальных и касательных напряжений) | (44) |
- Прочность по нормальным напряжениям может проверяться с учётом, или без учёта развития пластических деформаций.
 Возможность учёта развития пластических деформаций задаётя пользователем в параметрах конструирования. При этом можно руководствоваться разд. 8.1. Следует отметить, что в настоящей редакции СП 16.13330.2011, в связи с отсутствием коэффициентов учёта пластики для полного пластического шарнира, конструкции 3 класса по виду напряжённого состояния (полный пластический шарнир) считаются так же, как и конструкции 2 класса (ограниченное развитие пластики).
Возможность учёта развития пластических деформаций задаётя пользователем в параметрах конструирования. При этом можно руководствоваться разд. 8.1. Следует отметить, что в настоящей редакции СП 16.13330.2011, в связи с отсутствием коэффициентов учёта пластики для полного пластического шарнира, конструкции 3 класса по виду напряжённого состояния (полный пластический шарнир) считаются так же, как и конструкции 2 класса (ограниченное развитие пластики).
В случае допустимости расчета с учетом развития пластических деформаций программой выполняется проверка фактического наличия пластики. Для этого выполняются две проверки:
- проверка 1 – с учетом развития пластических деформаций;
- проверка 2 – без учета развития пластических деформаций.
Если прочность по проверке 1 обеспечивается, а по проверке 2 – нет, то элемент в данном сечении действительно работает с учетом развития пластических деформаций. И только в этом случае производится учет пластики в дальнейших проверках устойчивости и местной устойчивости.
Формулы для проверки прочности по нормальным напряжениям, указанные в таблице 2 и используемые в программе, учитывают все составляющие усилий в рассматриваемом сечении.
- Прочность по касательным напряжениям проверяется по формулам (42) в основе которых лежит формула Журавского.
- Прочность по приведенным напряжениям (совместное действие нормальных и касательных напряжений) проверяется по формулам теории прочности (44).
Общая устойчивость
Таблица 3.
| Проверки общей устойчивости | Обозначение | Формулы проверок |
| СП 16.13330.2011 | ||
| Устойчивость плоской формы изгиба | | (70) – без учёта стеснённого кручения. |
| Устойчивость по изгибной форме | | (109), (120), (121) |
| Устойчивость по изгибно-крутильной форме | | (111) |
| Устойчивость стержней, подверженных сжатию и изгибу в двух главных плоскостях | | (116) |
- Устойчивость плоской формы изгиба
Проверка устойчивости плоской формы изгиба (по φb) производится для открытых профилей следующих типов: двутавр симметричный, двутавр несимметричный, тавр, швеллер, а также для полосы. При определении коэффициента устойчивости при изгибе φb используется расчётная длина lef b, которая задаётся пользователем по указаниям пунктов 8.4.2 и часто равна расчётной длине элемента в плоскости минимальной жёсткости. Коэффициент φb определяется в соответствии с указаниями приложения Ж. Все задаваемые исходные данные соответствуют таблицам указанных приложений. Если заранее известно, что для рассматриваемого конструктивного элемента такая проверка не понадобится или вид нагрузки и загруженный пояс определить невозможно (например, колонна каркаса здания), рекомендуется для симметричных двутавров и швеллеров задать балочную схему работы, два и более боковых закреплений, а для несимметричных двутавров и тавров задать вид нагрузки, вызывающий чистый изгиб.
При определении коэффициента устойчивости при изгибе φb используется расчётная длина lef b, которая задаётся пользователем по указаниям пунктов 8.4.2 и часто равна расчётной длине элемента в плоскости минимальной жёсткости. Коэффициент φb определяется в соответствии с указаниями приложения Ж. Все задаваемые исходные данные соответствуют таблицам указанных приложений. Если заранее известно, что для рассматриваемого конструктивного элемента такая проверка не понадобится или вид нагрузки и загруженный пояс определить невозможно (например, колонна каркаса здания), рекомендуется для симметричных двутавров и швеллеров задать балочную схему работы, два и более боковых закреплений, а для несимметричных двутавров и тавров задать вид нагрузки, вызывающий чистый изгиб.
Для сечений из несимметричных двутавров или тавров в программе отсутствует проверка устойчивости плоской формы изгиба для консолей, по причине отсутствия указаний для такой проверки консолей в действующих нормах.
Поскольку для сечений из полосы в нормах отсутствуют указания для проверки устойчивости плоской формы изгиба, в программе определение коэффициента устойчивости при изгибе φb производится по формулам (Ж. 1), (Ж.2).
1), (Ж.2).
- Устойчивость по изгибной форме.
Важным вопросом при выполнении этой проверки является определение расчётных длин элементов. Расчётные длины задаются пользователем. При этом он может руководствоваться разделом 10, или специальной литературой (например, С. Д. Лейтес «Справочник по определению свободных длин элементов стальных конструкций», Москва, 1963 г).
Для сечений из одиночного уголка пользователь должен задать радиус инерции, используемый для данной проверки. При этом следует руководствоваться п. 10.1.4, 10.2.2 и 10.2.3.
Следует отметить, что в соответствии со всеми рассматриваемыми нормами коэффициент продольного изгиба при внецентренном сжатии не может быть больше коэффициента продольного изгиба при центральном сжатии (см. примечание п. 2 к таблице коэффициентов в рассматриваемых нормах). Поэтому проверка устойчивости центрально сжатых элементов рассматривается как частный случай проверки устойчивости по изгибной форме сжато-изогнутых элементов.
Для коробчатых сечений и для сечений из сплошного прямоугольника (полосы) обозначение соответствует проверке по формулам (121), соответственно обозначение – по формулам (120).
Для сечения из одиночного швеллера при наличии изгиба в плоскости большей жёсткости значения коэффициента формы сечения принимаются как для симметричного двутавра, о чём выводится соответствующее предупреждение.
Для несимметричных двутавров общего вида с произвольным соотношением площадей большей и меньшей полок, в нормах отсутствуют значения коэффициента формы сечения
. В программе коэффициент определяется с помощью кубической интерполяции между приведенными в нормах типами сечений. Параметром для интерполяции служит коэффициент (осевой коэффициент асимметрии несимметричного двутавра), где Afc и Аft соответственно площадь сжатой и растянутой полки.
В программе определяется значение коэффициента для каждого из перечисленных типов сечений, после чего между этими данными производится кубическая интерполяция по фактическому значению аk рассматриваемого профиля. Об этом выводится соответствующее предупреждение.
Об этом выводится соответствующее предупреждение.
Для сечений из круглой трубы или сплошного круглого сечения при проверке устойчивости по изгибной форме:
- если расчётные длины элемента в обеих плоскостях равны, т. е. если , используется результирующий момент, равный геометрической сумме моментов в двух взаимно-перпендикулярных направлениях: ;
- если , выполняются две независимые проверки: относительно оси Y1 с использованием момента Му и расчётной длины , и относительно оси Z1 с использованием момента Мz и расчётной длины .
- Устойчивость по изгибно-крутильной форме
Проверка производится по формулам (111.
Для сечения из одиночного швеллера при наличии изгиба в плоскости большей жёсткости значения коэффициентов α и β принимаются как для симметричного двутавра, о чём выводится соответствующее предупреждение.
При относительных эксцентриситетах в плоскости большей жёсткости параметр с определяется по формуле (43) полученной из условия (имеется в виду, что плоскость большей жёсткости X10Z1). При этом, в соответствии с указаниями п. 9.2.4 [9.11коэффициент φb, входящий в эту формулу определяется как для балки с двумя и более боковыми закреплениями, независимо от заданных пользователем.
При этом, в соответствии с указаниями п. 9.2.4 [9.11коэффициент φb, входящий в эту формулу определяется как для балки с двумя и более боковыми закреплениями, независимо от заданных пользователем.
Программой предусмотрена проверка устойчивости также и для растянуто-изогнутых элементов. Проверка производится на основании формулы
(1)
Сила растяжения в этом случае оказывает разгружающее действие, но это не гарантирует устойчивость сжатого пояса элемента.
Для сечения из полосы в нормах нет указаний для проверки устойчивости по изгибно-крутильной форме. Коэффициент с к формуле (111) определяется по формуле (2), полученной из условия (3
)
(2)
(3)
При проверке местной устойчивости стенок учёт локальных напряжений не предусмотрен. Предполагается также отсутствие продольных рёбер жёсткости. Наличие и шаг поперечных рёбер жёсткости задаёт пользователь, руководствуясь п. 8.5.9, п. 9.4.4. Для изгибаемых элементов отсутствие поперечных рёбер жёсткости приводит к увеличению толщины стенки, которая в этом случае проверяется из условия по требованию п. 8.5.9. В то же время программа не контролирует необходимость постановки поперечных рёбер жёсткости для сжатых и сжато-изогнутых элементов по п. 9.4.4, поскольку эти требования являются конструктивными и не влияют на расчёт.
Наличие и шаг поперечных рёбер жёсткости задаёт пользователь, руководствуясь п. 8.5.9, п. 9.4.4. Для изгибаемых элементов отсутствие поперечных рёбер жёсткости приводит к увеличению толщины стенки, которая в этом случае проверяется из условия по требованию п. 8.5.9. В то же время программа не контролирует необходимость постановки поперечных рёбер жёсткости для сжатых и сжато-изогнутых элементов по п. 9.4.4, поскольку эти требования являются конструктивными и не влияют на расчёт.
При проверке местной устойчивости коробчатых сечений, в общем случае, при наличии изгибающих моментов в обоих главных направлениях (Му ≠ 0, Мz ≠ 0), необходимо определить, какие из граней коробки считать стенками, а какие полками.
Таблица 4.
| Центральное сжатие. Стенками считаются все 4 стороны | Внецентренное сжатие вокруг оси Y1. Стенками считаются стороны, параллельные Z1 | Изгиб вокруг оси Y1. Стенками считаются стороны, параллельные оси Z1 Стенками считаются стороны, параллельные оси Z1 | |
| Внецентренное сжатие вокруг оси Z1. Стенками считаются стороны, параллельные оси Y1 | Внецентренное сжатие в двух направлениях. Стенками считаются стороны, параллельные оси Z1 | Стенками считаются стороны, параллельные оси Z1 | |
| Изгиб вокруг оси Z1. Стенками считаются стороны, параллельные оси Y1 | Стенками считаются стороны, параллельные оси Y1 | Изгиб в двух направлениях. Стенками считаются стороны, параллельные оси Z1 |
Второе предельное состояние
Прогибы
Прогибы элементов или конструктивных элементов проверяются в направлении их локальных осей Y1 и Z1. Необходимость такой проверки при подборе или проверке стальных конструкций задаётся пользователем на основании приложения Е СП 20.13330.2011 или других нормативных документов. При этом используются нормативные (эксплуатационные) значения постоянных нагрузок и длительные нагрузки, или длительно действующая часть кратковременных нагрузок со своими коэффициентами сочетаний. Такой подход справедлив для конструкций, загруженных постоянными, полезными, снеговыми и другими нагрузками, имеющими длительно действующую часть. К таким конструкциям относятся, например, стропильные балки, ригели покрытия, прогоны покрытия, балки и ригели перекрытий, балки рабочих и обслуживающих площадок, лестничные косоуры и марши, балки балконов и лоджий. Опоры конструктивных элементов (места, где прогибы принимаются равными нулю) задаются с помощью раскреплений. Если заданы раскрепления конструктивного элемента, то его прогиб считается относительно прямой линии, соединяющей эти раскрепления. При отсутствии раскреплений принимается полное перемещение сечений конструктивного элемента в составе расчётной схемы. Необходимость задания раскреплений определяет пользователь. Следует обратить внимание, что в режиме подбора сечения конструктивного элемента принято, что величина его прогиба изменяется обратно пропорционально изгибной жёсткости ЕI рассматриваемого конструктивного элемента и не учитывает перемещение других элементов расчётной схемы.
Такой подход справедлив для конструкций, загруженных постоянными, полезными, снеговыми и другими нагрузками, имеющими длительно действующую часть. К таким конструкциям относятся, например, стропильные балки, ригели покрытия, прогоны покрытия, балки и ригели перекрытий, балки рабочих и обслуживающих площадок, лестничные косоуры и марши, балки балконов и лоджий. Опоры конструктивных элементов (места, где прогибы принимаются равными нулю) задаются с помощью раскреплений. Если заданы раскрепления конструктивного элемента, то его прогиб считается относительно прямой линии, соединяющей эти раскрепления. При отсутствии раскреплений принимается полное перемещение сечений конструктивного элемента в составе расчётной схемы. Необходимость задания раскреплений определяет пользователь. Следует обратить внимание, что в режиме подбора сечения конструктивного элемента принято, что величина его прогиба изменяется обратно пропорционально изгибной жёсткости ЕI рассматриваемого конструктивного элемента и не учитывает перемещение других элементов расчётной схемы. Если при наличии раскреплений это предположение справедливо, то при их отсутствии такой подход может привести к неправильному результату. Поэтому в случае обоснованного отсутствия раскреплений окончательный расчёт сечений должен быть выполнен в режиме проверки.
Если при наличии раскреплений это предположение справедливо, то при их отсутствии такой подход может привести к неправильному результату. Поэтому в случае обоснованного отсутствия раскреплений окончательный расчёт сечений должен быть выполнен в режиме проверки.
Предельно допустимые прогибы задаются пользователем. При этом в каждом из направлений он может задать как величину прогиба в миллиметрах или в долях пролёта, так и автоматический выбор предельного прогиба по п. 2 таблицы Е.1 СП 20.13330.2011.
Для конструкций, у которых ограничены горизонтальные прогибы и перемещения от ветра по п. Е.2.4.1, Е.2.4.3, Е.2.4.4 СП 20.13330.2011 следует выполнить дополнительную проверку таких прогибов по локальным эпюрам перемещений, либо проверку горизонтальных перемещений соответствующих узлов от нормативных (эксплуатационных) значений ветровых нагрузок. К таким конструкциям относятся, например, колонны каркаса, стойки фахверка, ригели фахверка, опоры конвейерных галерей.
Проверку прогибов сложных стержневых систем, например, стропильных ферм или структурных блоков покрытия, следует выполнять по перемещениям характерных узлов в различных комбинациях загружений (с помощью РСН).
Гибкость
Необходимость такой проверки задаётся пользователем. Проверка гибкости конструктивных элементов производится на основании п. 10.4.1, 10.4.2 СП 16.13330.2011. Величину предельно допустимой гибкости задаёт пользователь. При этом он может задать требуемую величину сам, либо воспользоваться подсказкой программы, выбрав нужную строку из предлагаемых таблиц действующих норм.
Следите за нашими новостями и задавайте вопросы на форуме.
Расчет нагрузки на полку стеллажа для складов
Многие производственные и торговые предприятия нуждаются в складах для хранения своей продукции, для чего удобнее всего использовать специальные паллетные, сборные и полочные стеллажи из металла. Они способны справляться с высокой статической нагрузкой, сохраняя свои изначальные параметры в плане прочности и надежности на протяжении всего эксплуатационного срока. Чтобы обеспечить безопасность груза, а также рабочего персонала, задействованного в работе склада, необходимо знать максимально нагрузку на складской стеллаж.
Все производители, выпускающие складские стеллажи в соответствии с требованиями ГОСТ 28766-90, обязаны указывать в паспорте на конструкцию максимально разрешенную нагрузку. Проектный расчет нагрузки рассчитывается в соответствии с технологией, указанной в СНиПе 2.01.07-85. Просчитать максимальную нагрузку как на отдельную полку, так и на весь стеллаж, можно и самостоятельно. В данной статье мы расскажем о том, какие нюансы потребуется учесть при правильном расчете нагрузки, что позволит получить объективные данные.
Содержание
Главные критерии при проведении испытаний
Учитывая особое значение такого показателя, как грузоподъемность полки стеллажа, заказчик может самостоятельно провести соответствующие испытания. При выполнении операции в расчет берут 3 главных показателя:
- Общая устойчивость стеллажа при полной (максимальной) загрузке всех его полок.
- Прочность, которая определяется путем сопротивления стального сплава нагрузкам с учетом внутренних напряжений.

- Жесткость, главным показателем которой является определенный предел прогиба полок стеллажа.
Показатели устойчивости и жесткости конструкции конкретной модели увеличиваются путем замены стандартной крестовины на балку жесткости. Цельнокатаный профиль, в котором отсутствуют сварные швы, будет более прочным, что также обуславливает его более высокую стоимость.
Нагрузки, разрешенные на полки стеллажей
Планируя приобрести и установить конструкцию для хранения продукции, стоит учесть, что нагрузка на каждую полку может быть от 120 до 1300 кг. В зависимости от максимально возможной нагрузки на стойку, все складские стеллажи делятся на следующие категории:
- 500-750 кг – легкие.
- 1100-1600 кг – средние.
- До 32000 кг – мезонинного и паллетного типов.
Каждая модель, представленная сегодня на рынке, отличается вместимостью полок, шириной и высотой конструкций. Большая часть стеллажей часть является универсальной, поэтому может быть установлена не только на складе, но также в подвале и даже офисном помещения для хранения архивной и бумажной документации.
Основные типы стальных стеллажей
Главным показателем и характеристикой каждого металлического стеллажа является нагрузка, в связи с чем именно на это стоит в первую очередь обращать внимание при выборе. В соответствии с утвержденной классификацией все стеллажи делятся на следующие типы:
1. Стеллажи с грузоподъемностью 120 кг на одну полку
Изделия имеют сборно-разборную конструкцию, что упрощает их транспортировку и доставку на конкретный объект. Чаще всего устанавливаются на складах, где вес хранимой продукции не превышает 120 кг, благодаря чему исключается риск перегруза полки. В подавляющем большинстве случаев такие модели применяют в подсобных хозяйствах, гаражах, а также офисных помещениях различных компаний с целью хранения архивных документов. Благодаря перфорации стоек высота полок является регулируемой, что очень удобно для регулировки в соответствии с технологическими нуждами.
2. Стеллажи с грузоподъемностью 200 кг на одну полку
В отличие от предыдущих моделей, такие стеллажи имеют не только основные, но и дополнительные ребра жесткости, дающие возможность выдерживать вес в пределах 200 кг. Хорошая жесткость и устойчивость конструкции к статической нагрузке обуславливается усиленными болтовыми соединениями. Стеллажи такого типа могут располагаться уступом, лесенкой или же в линию. Всё сооружение состоит из горизонтальных полок и вертикальных стоек, к которым они прикрепляются. Стоит отметить, что в большинстве моделей крепеж уже включен в комплект (включая подпятники), поэтому приобретать дополнительно ничего не нужно.
Хорошая жесткость и устойчивость конструкции к статической нагрузке обуславливается усиленными болтовыми соединениями. Стеллажи такого типа могут располагаться уступом, лесенкой или же в линию. Всё сооружение состоит из горизонтальных полок и вертикальных стоек, к которым они прикрепляются. Стоит отметить, что в большинстве моделей крепеж уже включен в комплект (включая подпятники), поэтому приобретать дополнительно ничего не нужно.
3. Стеллажи с грузоподъемностью 300 кг на одну полку
Данные модели складских стеллажей выполняются также с усиленными ребрами жесткости, которые обеспечивают высокую грузоподъемность каждой полки. Стеллаж отличается легкостью сборки, поскольку крепление осуществляется при помощи специальных зацепов. Это в свою очередь позволяет в случае производственной необходимости свободно менять высоту полок. Несущими опорами являются вертикальные рамы, закрепленные стяжками, а также крестовина жесткости, которая монтируется в районе задней стенки. В качестве главного материала используется оцинкованная сталь, надежно защищенная от коррозионных процессов.
4. Стеллажи среднегрузовые с грузоподъемностью 500 кг на одну полку
Сооружения выполнены из конструкционной стали, покрытой слоем цинка. Для большей устойчивости стойки прикреплены к полу анкерными болтами, что надежно защищает конструкцию от случайного опрокидывания под нагрузкой. Перфорационные отверстия в стойках позволяют легко выставлять требуемую высоту. Система крепления предусматривает не болтовые соединения, а универсальные зацепы. В комплектации к стеллажам также поставляются еще и выравнивающие пластины, позволяющие установить конструкцию строго горизонтально даже при неровной поверхности.
5. Грузовые металлические стеллажи с нагрузкой на полку 1 000–1 500 кг
Самые мощные и крепкие стеллажи, обеспечивающие хранение груза большой массы. Как и предыдущие модели, они имеют зацепы, а также перфорационные отверстия в несущих стойках, что позволяет регулировать высоту. Все зацепы снабжены специальными фиксаторами, которые надежно защищают от случайного выпадения. В качестве настила полок используется не только металл, но и также фанера и ДСП. Такие стеллажи обязательно прикручиваются к полу анкерными болтами.
В качестве настила полок используется не только металл, но и также фанера и ДСП. Такие стеллажи обязательно прикручиваются к полу анкерными болтами.
Зная все типы металлических стеллажей и их особенности, можно подобрать ту модель, которая соответствует поставленным целям и задачам.
Расчетная нагрузка на сборно-разборный стеллаж
Правильный расчет нагрузки на стеллаж обеспечивает безопасность не только хранимого груза, но и рабочего персонала. Требованиями ГОСТа устанавливаются нормативные расчеты жесткости, устойчивости и прочности каждого конкретного изделия, стандарт которого равняется 10% (для обычных) или 25% (для усиленных). Все используемые методики расчета нагрузок, применяемые для стальных конструкций, изложены в ГОСТе 28766-90.
Особенности выбора стеллажа с учетом нагрузки на полки
Перед покупкой металлической мебели для склада следует обратить внимание на:
- 1. Загруженность полки. В теории предполагается, что груз будет распределен по всей поверхности полки равномерно, однако на практике такое происходит редко.
 Поэтому следует знать, что при грузоподъемности полки в 200 кг и ее длине в 1 метр, на каждые 10 см. полки должно приходиться не более 20 кг.
Поэтому следует знать, что при грузоподъемности полки в 200 кг и ее длине в 1 метр, на каждые 10 см. полки должно приходиться не более 20 кг. - 2. Нагрузки на стойки. При покупке конструкции обращают внимание на несущую способность стоек, обозначающими предел, при которой они не деформируются. Необходимо также помнить о естественном сокращении максимальной нагрузки с увеличением высоты расположения полки.
- 3. Нагрузка на конструкцию. Данный параметр указывается в эксплуатационном паспорте к стеллажу.
- 4. Наименьшее количество полок. Существует прямая зависимость всего стеллажа от количества расположенных в нем полок — чем их больше, тем жестче каркас конструкции.
- 5. Наибольшее расстояние между 2-мя полками. Производитель обязательно указывает максимальное расстояние между горизонтальными полками, которого следует придерживаться, чтобы не нарушать несущую способность и грузоподъемность сооружения.
- 6. Наибольшая высота нижней полки.
 При загрузке соблюдают правило: чем выше полка от земли, тем нагрузка на нее должна быть меньшей.
При загрузке соблюдают правило: чем выше полка от земли, тем нагрузка на нее должна быть меньшей. - 7. Понятие «параметры загрузки стеллажа». Любой производитель, который проектирует и конструирует складские стеллажи, выполняет специальный расчет, касающийся предельных нагрузок, при которых изделие не деформируется. Данные показатели отражены в эксплуатационном паспорте.
Компания ООО «ФеррАМ» предлагает большой ассортимент металлических стеллажей, отличающихся габаритными размерами, конфигурацией и грузоподъемностью. Все наши конструкции являются надежными и долговечными, поскольку изготавливаются из качественных материалов и поставляются нами с эксплуатационными паспортами. Продажа стеллажей из металла осуществляется оптом и в розницу по доступным ценам. Ждем ваших звонков по телефону +375 (17) 360-93-12!
Угол отклонения задан Калькулятор длины кривой
✖Длина кривой определяется как длина дуги в параболических кривых. | A.U. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖Радиус кривой – радиус окружности, часть которой, скажем, дуга принимается во внимание. 8А.Е. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% |
✖ Центральный угол — это угол, вершина (вершина) которого является центром O окружности, а катеты (стороны) — это радиусы, пересекающие окружность в двух различных точках A и B. | КругЦиклГрадусГрадМилмиллирадианМинутаМинуты дугиТочкаКвадрантЧетвертькругРадианОборотПрямой УголСекундаПолукругСекстантаЗнакПоворот | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Угол отклонения при заданной длине кривой Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Длина кривой: 100 метров —> 100 метров Преобразование не требуется
Радиус кривой: 50 метров —> 50 метров Преобразование не требуется
ШАГ 2: Вычислите формулу
ШАГ 3: Преобразуйте результат в единицу измерения
2 Радиан —> 114,5915586 Градус (проверьте преобразование здесь)
< 10+ калькуляторов кривыхУгол отклонения при заданной длине кривой Формула
Центральный угол = длина кривой/радиус кривой
∠ центральный = Л/П
Что означает построение кривой?
Разметка кривой означает размещение различных точек на равных и удобных расстояниях по длине кривой. Расстояние между любыми двумя последовательными точками называется интервалом привязки. Поскольку измерять интервал колка по дуге нецелесообразно, его измеряют по хорде.
Расстояние между любыми двумя последовательными точками называется интервалом привязки. Поскольку измерять интервал колка по дуге нецелесообразно, его измеряют по хорде.
Как рассчитать угол отклонения, учитывая длину кривой?
Угол отклонения при заданной длине кривой Калькулятор использует центральный угол = длина кривой/радиус кривой для расчета центрального угла. Угол отклонения при заданной длине кривой также называется внутренним центральным углом. Центральный угол — это угол, вершина которого является центром окружности, а катеты (стороны) — это радиусы, пересекающие окружность в двух различных точках. Центральный угол обозначается символом ∠ центральный .
Как рассчитать угол отклонения при заданной длине кривой с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для угла отклонения с учетом длины кривой, введите длину кривой (L) и радиус кривой (R) и нажмите кнопку расчета. Вот как можно объяснить расчет угла отклонения с учетом длины кривой с заданными входными значениями -> 114,5916 = 100/50 .
Вот как можно объяснить расчет угла отклонения с учетом длины кривой с заданными входными значениями -> 114,5916 = 100/50 .
Часто задаваемые вопросы
Что такое угол отклонения с учетом длины кривой?
Угол отклонения при заданной длине кривой также называется внутренним центральным углом. Центральный угол — это угол, вершина которого является центром окружности, а катеты (стороны) — это радиусы, пересекающие окружность в двух различных точках. кривая/радиус кривой . Длина кривой определяется как длина дуги в параболических кривых, а Радиус кривой — это радиус окружности, часть которой, например, дуга, принимается во внимание.
Как рассчитать угол отклонения, учитывая длину кривой?
Угол отклонения при заданной длине кривой также называется внутренним центральным углом. Центральный угол — это угол, вершина которого является центром окружности, а катеты (стороны) — это радиусы, пересекающие окружность в двух различных точках. Он рассчитывается по формуле Центральный угол = длина кривой/радиус кривой . Чтобы рассчитать угол отклонения с учетом длины кривой, вам потребуется длина кривой (L) и радиус кривой 9.0101 (R) . С помощью нашего инструмента вам нужно ввести соответствующие значения для длины кривой и радиуса кривой и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Он рассчитывается по формуле Центральный угол = длина кривой/радиус кривой . Чтобы рассчитать угол отклонения с учетом длины кривой, вам потребуется длина кривой (L) и радиус кривой 9.0101 (R) . С помощью нашего инструмента вам нужно ввести соответствующие значения для длины кривой и радиуса кривой и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Доля
Скопировано!
Калькулятор угла отклонения первой хорды
✖Первая подхорда — это первая хорда, нарисованная на кривой для построения кривой с использованием смещений от касательных.ⓘ Первая подхорда [C 1 ] | А.Е. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖Радиус кривой – радиус окружности, часть которой, скажем, дуга принимается во внимание. 8А.Е. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% |
✖Угол отклонения 1 — это угол между первой подхордой кривой и отклоненной линией с равным измерением первой подхорды от точки касания. | КругЦиклГрадусГрадМилмиллирадианМинутаМинуты дугиТочкаКвадрантЧетвертькругРадианОборотПрямой УголСекундаПолукругСекстантаЗнакПоворот | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Угол отклонения решения первой хорды
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Первая подхорда: 5 метров —> 5 метров Преобразование не требуется
Радиус кривой: 50 метров —> 50 метров Преобразование не требуется
ШАГ 2: Вычисление формулы
ШАГ 3: Преобразование результата в единицы измерения
0. 000872664625997165 Радиан —> 0.0500000000000094 Градус (Проверьте преобразование здесь)
000872664625997165 Радиан —> 0.0500000000000094 Градус (Проверьте преобразование здесь)
Формула угла отклонения первой хорды
Угол отклонения 1 = (Первая вспомогательная хорда/(2*Радиус кривой))*(pi/180)
δ 1 = (C 1 /(2*R))*(pi/180)
Какие существуют методы ранжирования кривой?
Кривая может быть установлена:
1. Линейными методами, где используются цепь и лента.
2. Угловыми или инструментальными методами, где используется теодолит с цепочкой или без нее.
Прежде чем приступить к нанесению кривой любым способом, необходимо определить точное положение точек касания, между которыми лежит кривая.
Как рассчитать угол отклонения первой хорды?
Калькулятор угла отклонения первой хорды использует Угол отклонения 1 = (первая подхорда/(2*радиус кривой))*(pi/180) для расчета угла отклонения 1. Угол отклонения первой хорды — это угол между первой подхорды и линии, отклоненной от первой хорды на равную длину от точки касания. Угол отклонения 1 обозначается цифрой δ 1 символ.
Угол отклонения первой хорды — это угол между первой подхорды и линии, отклоненной от первой хорды на равную длину от точки касания. Угол отклонения 1 обозначается цифрой δ 1 символ.
Как рассчитать угол отклонения первой хорды с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для угла отклонения первой хорды, введите первую подхорду (C 1 ) и радиус кривой (R) и нажмите кнопку расчета. Вот как можно объяснить расчет угла отклонения первой хорды с заданными входными значениями -> 0,05 = (5/(2*50))*(pi/180) .
Часто задаваемые вопросы
Что такое угол отклонения первой хорды?
Угол отклонения первой хорды – это угол между первой подхордой и линией, отклоненной от первой хорды равной длины от точки касания, и представляется как δ 1 = (C 1 /(2* R))*(pi/180) или Угол отклонения 1 = (Первая вспомогательная хорда/(2*Радиус кривой))*(pi/180) . Первая подхорда — это первая хорда, нарисованная на кривой для построения кривой с использованием смещений от касательных, а Радиус кривой — это радиус окружности, часть которой, скажем, дуга, принимается во внимание.
Первая подхорда — это первая хорда, нарисованная на кривой для построения кривой с использованием смещений от касательных, а Радиус кривой — это радиус окружности, часть которой, скажем, дуга, принимается во внимание.
Как рассчитать угол отклонения первой хорды?
Угол отклонения первой хорды — это угол между первой подхордой и линией, отклоненной от первой хорды равной длины от точки касания, рассчитывается с использованием Угол отклонения 1 = (Первая подхорда/(2*Радиус кривой ))*(пи/180) . Чтобы рассчитать угол отклонения первой хорды, вам потребуется первая подхорда (C 1 ) и радиус кривой (R) . С помощью нашего инструмента вам нужно ввести соответствующее значение для первой вспомогательной хорды и радиуса кривой и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Поделиться
Скопировано!
Строительные геодезические кривые Помощь | EZ-pdh.
 com
comИспользуйте поиск, чтобы быстро найти ответы на вопросы — откройте окно поиска (ctrl+f), затем введите ключевое слово из вопроса, чтобы перейти к этим терминам в материалах курса
ТОЧКИ КРИВОЙ
Автор Изучая этот курс, геодезист учится находить точки, используя углы и расстояния. При строительной съемке геодезист часто должен установить линию кривой для разметки дороги или какого-либо другого сооружения.
Геодезист может создавать кривые малого радиуса, обычно меньше длины ленты, удерживая один конец ленты в центре круга и вращая ленту по дуге, отмечая необходимое количество точек.
По мере увеличения радиуса и длины кривой использование ленты становится непрактичным, и геодезист должен использовать другие методы. Измеренные углы и расстояния по прямой обычно выбираются для определения местоположения выбранных точек, известных как пикеты, на окружности дуги.
ТИПЫ ГОРИЗОНТАЛЬНЫХ КРИВЫХ
Кривая может быть простой, сложной, обратной или спиральной (рисунок l). Составные и обратные кривые рассматриваются как комбинация двух или более простых кривых, тогда как спиральная кривая основана на переменном радиусе.
Составные и обратные кривые рассматриваются как комбинация двух или более простых кривых, тогда как спиральная кривая основана на переменном радиусе.
Простая
Простая кривая представляет собой дугу окружности. Это наиболее часто используемый. Радиус окружности определяет «резкость» или «плоскость» кривой. Чем больше радиус, тем «площе» кривая.
Составная
Геодезистам часто приходится использовать составную кривую из-за рельефа местности. Эта кривая обычно состоит из двух простых кривых, изгибающихся в одном направлении и соединенных вместе.
Реверс
Реверсивная кривая состоит из двух простых кривых, соединенных вместе, но изгибающихся в противоположных направлениях. Из соображений безопасности геодезист не должен использовать эту кривую без крайней необходимости.
Спираль
Спираль представляет собой кривую с различным радиусом, используемую на железных дорогах и некоторых современных автомагистралях. Он обеспечивает переход от касательной к простой кривой или между простыми кривыми в составной кривой.
Он обеспечивает переход от касательной к простой кривой или между простыми кривыми в составной кривой.
СТАНЦИОНИРОВАНИЕ
При маршрутных съемках геодезист нумерует станции от начала проекта. Например, 0+00 указывает на начало проекта. 15+52,96 указывает на точку в 1552,96 футах от начала. Полная станция составляет 100 футов или 30 метров, что составляет 15+00 и 16+00 полных станций. Плюсовая станция указывает точку между полными станциями. (15 + 52,96 — это плюсовая станция.) При использовании метрической системы геодезист не использует плюсовую систему нумерации станций. Номер станции просто становится расстоянием от начала проекта.
ЭЛЕМЕНТЫ ПРОСТОЙ КРИВОЙ
На рис. 2 показаны элементы простой кривой. Они описываются следующим образом, а их сокращения даны в скобках.
Точка пересечения (ТП)
Точка пересечения отмечает точку, в которой пересекаются прямые и задние касательные. Геодезист указывает ее как одну из станций предварительного хода.
Угол пересечения (I)
Угол пересечения — это угол отклонения в ТП. Геодезист либо вычисляет его значение по углам предварительного пикета, либо измеряет его в полевых условиях.
Радиус (R)
Радиус — это радиус окружности, дугой которой является кривая.
Точка кривизны (PC)
Точка кривизны — это точка, где начинается круговая кривая. Обратная касательная касается кривой в этой точке.
Точка касания (PT)
Точка касания — это конец кривой. Прямая касательная касается кривой в этой точке.
Длина кривой (L)
Длина кривой — это расстояние от ПК до ПТ, измеренное вдоль кривой.
Расстояние по касательной (T)
Расстояние по касательной — это расстояние по касательной от PI до PC или PT. Эти расстояния равны на простой кривой.
Центральный угол (�)
Центральный угол — это угол, образованный двумя радиусами, проведенными из центра окружности (0) к PC и PT. Центральный угол по величине равен углу I.
Центральный угол по величине равен углу I.
Длинная хорда (LC)
Длинная хорда — это хорда от PC до PT.
Внешнее расстояние (E)
Внешнее расстояние — это расстояние от ТП до середины кривой. Внешнее расстояние делит пополам внутренний угол в PI.
Средняя ордината (M)
Средняя ордината — это расстояние от середины кривой до середины длинной хорды. Продолжение средней ординаты делит центральный угол пополам.
Степень кривой (D)
Степень кривой определяет «резкость» или «плоскостность» кривой (рис. 3). Обычно используются два определения степени кривой: определение дуги и определение хорды.
Определение дуги. В определении дуги указано, что степень изгиба (D) — это угол, образованный двумя радиусами, проведенными из центра окружности (точка O на рис. 3) к концам дуги длиной 100 футов или 30,48 метра. В этом определении степень изгиба и радиус обратно пропорциональны по следующей формуле:
По мере увеличения степени изгиба радиус уменьшается. Следует отметить, что для заданного угла пересечения или центрального угла при использовании определения дуги все элементы кривой обратно пропорциональны степени кривой. Это определение в основном используется гражданскими инженерами при строительстве дорог.
Следует отметить, что для заданного угла пересечения или центрального угла при использовании определения дуги все элементы кривой обратно пропорциональны степени кривой. Это определение в основном используется гражданскими инженерами при строительстве дорог.
Английская система . Подставляя D = 1° и длину дуги = 100 футов, получаем
Метрическая система. В метрической системе, используя длину дуги 30,48 метра и подставляя D = 1°, мы получаем
Определение хорды. Определение хорды гласит, что степень изгиба представляет собой угол, образованный двумя радиусами, проведенными от центра окружности (точка O на рис. 3) к концам хорды длиной 100 футов или 30,48 метра. Радиус вычисляется по следующей формуле:
Радиус и степень изгиба не обратно пропорциональны, хотя, как и в определении дуги, чем больше степень изгиба, тем «острее» кривая и меньше радиус. Определение хорды используется в основном на железных дорогах в гражданской практике, а также для автомобильных и железных дорог военными.
Определение хорды используется в основном на железных дорогах в гражданской практике, а также для автомобильных и железных дорог военными.
Английская система. Подставляя D = 1° и учитывая Sin ½ 1 = 0,0087265355
Метрическая система. Using a chord 30.48 meters long, the surveyor computes R by the formula
Substituting D = 1° and given Sin ½ 1° = 0.0087265335, solve for R as follows:
Chords
On кривые с большим радиусом, нецелесообразно разбивать кривую, определяя центр окружности и поворачивая дугу рулеткой. Геодезист размещает эти кривые, разбивая концы ряда хорд (рис. 4). Поскольку концы хорд лежат на окружности кривой, геодезист определяет дугу в поле. Длина хорд зависит от степени изгиба. Чтобы уменьшить несоответствие между расстоянием по дуге и расстоянием по хорде, геодезист использует следующие длины хорды:
Приведенные выше длины хорд — это максимальные расстояния, при которых несоответствие между длиной дуги и длиной хорды будет находиться в пределах допустимой погрешности для наложения ленты, которая составляет 0,02 фута на 100 футов для большинства строительных съемок. В зависимости от местности и потребностей мастеров проекта геодезист может разметить кривую с более короткими или более длинными хордами, чем рекомендуется.
В зависимости от местности и потребностей мастеров проекта геодезист может разметить кривую с более короткими или более длинными хордами, чем рекомендуется.
Углы отклонения
Углы отклонения представляют собой углы между касательной и концами хорд от ПК. Геодезист использует их для определения направления, в котором должны быть проложены пояса. Сумма углов отклонения всегда равна половине угла I. Эта сумма служит проверкой рассчитанных углов отклонения.
ФОРМУЛЫ ПРОСТОЙ КРИВОЙ
Следующие формулы используются для расчета простой кривой. Все формулы, кроме отмеченных, применимы как к определениям дуги, так и к хорде.
L — расстояние вокруг дуги для определения дуги или расстояние вдоль хорды для определения хорды.
В следующих формулах C равно длине хорды, а d равно углу отклонения . Все формулы точны для определения дуги и приближены для определения хорды.
Эта формула дает ответ в градусах.
в метрической системе. Ответ будет через несколько минут.
Ответ будет через несколько минут.
РЕШЕНИЕ ПРОСТОЙ КРИВОЙ
Чтобы решить простую кривую, геодезист должен знать три элемента. Первые два — это значение станции PI и угол I. Третье — это степень кривизны, которая указывается в спецификации проекта или рассчитывается с использованием одного из элементов, ограниченных рельефом местности (см. раздел II). Геодезист обычно определяет угол PI и I на предварительном ходе дороги. Это также можно сделать с помощью триангуляции, когда PI недоступен.
Определение аккорда
В примере использовались шестизначные натуральные тригонометрические функции из таблицы A-1. Когда калькулятор используется для получения тригонометрических функций, результаты могут незначительно отличаться. Предположим, что известно следующее: PI = 18+00, I = 45 и D = 15°.
Определение хорды (футы)
Хорды. Так как степень изгиба составляет 15 градусов, длина хорды составляет 25 футов. Геодезист обычно размещает первую веху после ПК на положительной станции, кратной длине хорды. Геодезист размечает осевую линию дороги с интервалами 10, 25, 50 или 100 футов между кривыми. Таким образом, сторона уровня не путается, когда уровни профиля проходят по центральной линии. Первая ставка после ПК для этой кривой будет на пикете 16+50. Таким образом, длина первой хорды или подхорда составляет 8,67 фута. Точно так же будет подхорда в конце кривой от станции 19.+25 к ПТ. Эта подхорда будет 16,33 фута. Геодезист обозначает подхорду в начале С1 и в конце С2 (рис. 2).
Геодезист обычно размещает первую веху после ПК на положительной станции, кратной длине хорды. Геодезист размечает осевую линию дороги с интервалами 10, 25, 50 или 100 футов между кривыми. Таким образом, сторона уровня не путается, когда уровни профиля проходят по центральной линии. Первая ставка после ПК для этой кривой будет на пикете 16+50. Таким образом, длина первой хорды или подхорда составляет 8,67 фута. Точно так же будет подхорда в конце кривой от станции 19.+25 к ПТ. Эта подхорда будет 16,33 фута. Геодезист обозначает подхорду в начале С1 и в конце С2 (рис. 2).
Углы отклонения. После определения подхордов геодезист вычисляет углы отклонения по формулам. Технически формулы для определения дуги не точны для определения хорды. Однако, когда для разбивки кривой используется одноминутный инструмент, геодезист может использовать их для любого определения. Углы отклонения
Количество полных хорд вычисляется путем вычитания первого плюсового пикета, кратного длине хорды, из последнего плюсового пикета, кратного длине хорды, и деления разницы на стандартную (стандартную) длину хорды. Таким образом, у нас есть (19+25 – 16+50)-25 равно 11 полных аккордов. Поскольку имеется 11 хорд по 25 футов, сумма углов отклонения для 25-футовых хорд составляет 11 х 1°52,5’ = 20°37,5’.
Таким образом, у нас есть (19+25 – 16+50)-25 равно 11 полных аккордов. Поскольку имеется 11 хорд по 25 футов, сумма углов отклонения для 25-футовых хорд составляет 11 х 1°52,5’ = 20°37,5’.
Сумма d , d и отклонений для полных хорд равна
Геодезист должен отметить, что сумма углов отклонения равна половине угла I. Если полный прогиб не равен половине I, в расчетах допущена ошибка. После определения общего отклонения геодезист определяет углы для каждой станции на кривой. На этом этапе они округляются до наименьшего показания прибора, который будет использоваться в полевых условиях. Для этой задачи геодезист должен предположить, что будет использоваться одноминутный прибор. Углы отклонения криволинейной станции перечислены на стр. 6.
Особые случаи. Кривая, решенная на стр. 6, имеет угол I и степень кривой, значениями которых являются целые градусы. Когда угол I и градус кривой состоят из градусов и минут, процедура решения кривой не меняется, но геодезист должен позаботиться о подстановке этих значений в формулы для длины и углов отклонения. Например, если I = 42° 15’ и D = 5° 37’, геодезист должен изменить минуты в каждом угле на десятичную часть градуса, или D = 42,25000°, I = 5,61667°. Чтобы получить требуемую точность, геодезист должен преобразовать значения в пять знаков после запятой.
Например, если I = 42° 15’ и D = 5° 37’, геодезист должен изменить минуты в каждом угле на десятичную часть градуса, или D = 42,25000°, I = 5,61667°. Чтобы получить требуемую точность, геодезист должен преобразовать значения в пять знаков после запятой.
Альтернативный метод вычисления длины состоит в преобразовании угла I и степени кривой в минуты; таким образом, 42° 15’ = 2535 минут и 5° 37’ = 337 минут. Подстановка в формулу длины дает
Этот метод дает точный результат. Если геодезист переведет минуты в десятичную часть градуса с точностью до пяти знаков, получится тот же результат.
Поскольку сумма углов отклонения должна составлять половину угла I, возникает проблема, когда угол I содержит нечетное количество минут, а используемый инструмент является одноминутным. Поскольку геодезист обычно размечает PT перед прохождением кривой, общее отклонение будет проверкой PT. Следовательно, геодезист должен рассчитывать с точностью до 0,5 градуса. Если общее отклонение проверяется с точностью до минуты в поле, его можно считать правильным.
Таблицы кривых
Геодезист может упростить расчет простых кривых с помощью таблиц. В Таблице A-5 перечислены длинные хорды, средние ординаты, внешние и касательные для кривой 1 градуса с радиусом 5730 футов для различных углов пересечения. В Таблице A-6 перечислены поправки касательной и внешнего расстояния (определение хорды) для различных углов пересечения и степеней кривой.
Определение дуги. Поскольку степень кривой по определению дуги обратно пропорциональна другим функциям кривой, значения для кривой в один градус делятся на степень кривой, чтобы получить желаемый элемент. Например, в таблице A-5 указано расстояние по касательной и внешнее расстояние для угла I в 75 градусов, равное 4,39.6,7 фута и 1492,5 фута соответственно. Разделив на 15 градусов степень кривой, геодезист получает расстояние по касательной 293,11 фута и внешнее расстояние 99,50 фута.
Определение аккорда. Чтобы преобразовать эти значения в определение хорды, геодезист использует значения в таблице A-5. Из таблицы A-6 получена поправка 0,83 фута для тангенциального расстояния и для внешнего расстояния 0,29 фута.
Из таблицы A-6 получена поправка 0,83 фута для тангенциального расстояния и для внешнего расстояния 0,29 фута.
Геодезист добавляет поправки к касательному расстоянию и внешнему расстоянию, полученным из таблицы A-5. Это дает касательное расстояние 293,94 фута и внешнее расстояние 99,79 фута для определения хорды.
После извлечения касательных и внешних расстояний из таблиц геодезист вычисляет оставшуюся часть кривой.
СРАВНЕНИЕ ОПРЕДЕЛЕНИЙ ДУГИ И ХОРДЫ
Между геодезистами возникают недопонимания в области определения дуги и хорды. Следует помнить, что одно определение не лучше другого.
Различные элементы
Два разных круга используются для сравнения двух кривых с одинаковой степенью искривления. Разница в том, что один вычисляется по определению дуги, а другой — по определению хорды. Поскольку две кривые имеют разные радиусы, другие элементы также различны.
Определение 5730 футов
Некоторые инженеры предпочитают использовать значение 5730 футов для радиуса кривой в 1 градус и формулы определения дуги. По сравнению с чисто дуговым методом с использованием 5729,58 метод 5730 дает
По сравнению с чисто дуговым методом с использованием 5729,58 метод 5730 дает
расхождений менее чем на одну часть на 10000 частей. Это намного лучше, чем точность измерений, сделанных в полевых условиях, и приемлема во всех случаях, кроме самых крайних. Таблица A-5 основана на этом определении.
СХЕМА КРИВОЙ
Ниже описана процедура построения кривой с использованием одноминутного прибора с горизонтальным кругом, отсчитываемым вправо. Значения такие же, как те, которые используются для демонстрации решения простой кривой.
Настройка PC и PT
Когда инструмент находится на PI, оператор наводит на предыдущий PI и держит головной рулетщик на линии, пока измеряется касательное расстояние. Ставка устанавливается на линии и помечается, чтобы показать ПК и значение его станции.
Инструментарий теперь наводит инструмент на передний PI, и измеряется касательное расстояние, чтобы установить и отметить разбивку для PT.
Вывод кривой с ПК
Процедура выведения кривой с ПК описана ниже. Обратите внимание, что процедура зависит от того, поворачивает ли дорога влево или вправо.
Обратите внимание, что процедура зависит от того, поворачивает ли дорога влево или вправо.
Дорога поворачивает направо. Прибор настраивается на ПК с горизонтальной окружностью на 0°00’ на ПИ.
- Угол к ПТ измеряется, если ПТ виден. Этот угол будет равен половине угла I, если PC и PT расположены правильно.
- Не касаясь нижнего движения, на горизонтальной окружности устанавливается первый угол отклонения d1 (0° 39’). Инструментарий держит головной магнитофон на линии, в то время как расстояние до первого субаккорда, C1 (8,67 фута), измеряется от ПК, чтобы установить и отметить станцию 16 + 50.
- Теперь оператор устанавливает второй угол отклонения, d1+ dstd (2° 32’), на горизонтальной окружности. Лентомеры измеряют стандартную хорду (25 футов) от ранее установленной станции (16 + 50), в то время как инструментарий держит главного магнитофона на линии, чтобы установить станцию 16 + 75.
- Последующие пикеты размечаются таким же образом.
 Если работа выполнена правильно, последний угол отклонения будет указывать на PT, а последнее расстояние будет длиной подхорды C2 (16,33 фута) до PT.
Если работа выполнена правильно, последний угол отклонения будет указывать на PT, а последнее расстояние будет длиной подхорды C2 (16,33 фута) до PT.
Изгиб дороги влево. Как указано в процедурах, прибор занимает ПК и установлен на 0°00’, указывая на PI.
- Угол измеряется к PT, если это возможно, и вычитается из 360 градусов. Результат будет равен половине угла I, если PC и PT расположены правильно.
- Первое отклонение, dl (0° 39’), вычитается из 360 градусов, а остаток устанавливается на горизонтальной окружности. Первая подхорда, Cl (8,67 фута), измеряется от PC, а вешалка устанавливается на линию и отмечается пикет 16+50.
- Остальные станции устанавливаются путем вычитания их углов отклонения из 360 градусов и установки результатов на горизонтальных окружностях. Расстояния по хорде измеряются от ранее установленного пикета.
- Последняя станция, установленная перед PT, должна быть C2 (16,33 фута от PT), а ее отклонение должно равняться углу, измеренному в (1) выше, плюс последнее отклонение d2 (1° 14’).

Разметка кривой из промежуточной настройки
Если невозможно разбить всю кривую с ПК, геодезист должен использовать адаптацию вышеописанной процедуры.
- Разметьте как можно больше станций с ПК.
- Переместите прибор вперед к любой станции на кривой.
- Выберите другую уже установленную станцию и установите угол отклонения для этой станции на горизонтальном круге. Наведите на эту станцию инструментальный телескоп в обратном положении.
- Погрузите зрительную трубу и установите оставшиеся станции, как если бы инструмент был настроен на ПК.
Разметка кривой с PT
Если настройка на кривой была сделана, но по-прежнему невозможно установить все оставшиеся пикеты из-за какого-либо препятствия, геодезист может «вернуть» оставшуюся часть кривой с PT . Хотя эта процедура была разработана как метод обхода препятствий, она широко используется для построения кривых. При использовании «метода резервного копирования» геодезист устанавливает примерно половину пикетов кривой с ПК, а оставшуюся часть — с PT. При использовании этого метода любая ошибка кривой находится в ее центре, где она менее заметна.
При использовании этого метода любая ошибка кривой находится в ее центре, где она менее заметна.
Дорога поворачивает направо. Займите PT и наведитесь на PI с половиной угла I на горизонтальном круге. Инструмент теперь ориентирован так, что если наведется компьютер, инструмент будет показывать 0°00’. Остальные пикеты можно установить, используя их отклонения и расстояния по хорде от ПК или в обратном порядке от ПТ.
Дорога поворачивает налево. Займите PT и наведите PI на 360 градусов минус половина угла I на горизонтальном круге. Прибор должен показывать 0° 00’, если компьютер находится в поле зрения.
Установите оставшиеся пикеты, используя их отклонения и длины хорд, как если бы они были рассчитаны с помощью ПК, или путем вычисления отклонений в обратном порядке от PT.
КОРРЕКЦИЯ ХОРД
Часто геодезист должен прокладывать кривые более точно, чем это возможно при использовании ранее описанных длин хорд.
Для устранения несоответствия длины хорды и длины дуги необходимо скорректировать хорды, используя значения, взятые из номографии в таблице А-11. Это дает поправки, которые должны быть применены, если кривая была рассчитана по определению дуги.
В таблице A-10 приведены поправки, которые следует применять, если кривая была рассчитана по определению хорды. Геодезист должен помнить, что длина кривой, рассчитанная по определению хорды, была длиной вдоль хорды. На рисунке 5 показан пример, приведенный в таблице A-9. Расстояние по хорде от пикета 18+00 до пикета 19+00 равно 100 футам. Номинальная длина подхорд 50 футов. Таблицы A-9, A-10 и A-11 из FM 5-233 доступны на веб-сайте PDH.
ПРОМЕЖУТОЧНАЯ СТАВКА
Если геодезист хочет разместить веху на пикете 18+50, необходимо внести поправку на хорды, так как расстояние от 18+00 через 18+50 до 19+00 больше, чем хорда от 18+00 до 19+00. Поэтому к субхордам необходимо применить поправку, чтобы станция 19+00 оставалась на расстоянии 100 футов от 18+00. На рисунке 5, если длина хорды номинально составляет 50 футов, то поправка составляет 0,19 фута. Расстояние по хорде от 18+00 до 18+50 и от 18+50 до 19+00 будет равно 50,19.
На рисунке 5, если длина хорды номинально составляет 50 футов, то поправка составляет 0,19 фута. Расстояние по хорде от 18+00 до 18+50 и от 18+50 до 19+00 будет равно 50,19.
ОГРАНИЧЕНИЯ ПО МЕСТНОСТИ
Чтобы решить простую кривую, геодезист должен знать три части. Обычно это будут PI, угол I и степень кривой. Однако иногда особенности рельефа ограничивают размер различных элементов кривой. В этом случае геодезист должен определить степень искривления по ограничивающему фактору.
Недоступный PI
При определенных условиях может быть невозможно или нецелесообразно занимать PI. В этом случае геодезист находит элементы кривой, используя следующие шаги (рис. 6).
- Отметьте две невидимые точки A и B, по одной на каждой из касательных, чтобы линия AB (случайная линия, соединяющая касательные) не пересекала препятствие.
- Измерьте углы a и b, установив их в точках A и B.
- Измерьте расстояние AB.
- Вычислите недоступные расстояния AV и BV следующим образом:
- Определите касательное расстояние от PI до PC на основе степени искривления или другого заданного ограничивающего фактора.

- Расположите ПК на расстоянии T минус AV от точки A и PT на расстоянии T минус BV от точки B.
- Приступить к расчету и компоновке кривой.
Недоступный ПК
Когда ПК недоступен, как показано на рис. 7, а PI и PT установлены и легко доступны, геодезист должен установить местоположение смещенной станции на ПК.
- Поместите прибор на ПТ и отведите кривую назад, насколько это возможно.
- Выберите одну из станций (например, «P») на кривой, чтобы линия PQ, параллельная касательной AV, проходила мимо препятствия на PC.
- Вычислите и запишите длину линии PW так, чтобы точка W находилась на касательной к линии AV, а линия PW была перпендикулярна касательной. Длина линии PW = R (l – Cos dp), где dp – часть центрального угла, образуемая AP и равная удвоенному углу отклонения P.
- Установите точку W на касательной, настроив инструмент при PI и угле отвода V (V = 180° – I). Это наведет инструмент вдоль касательной. Поверните рулетку, используя рассчитанную длину линии PW и линию визирования, чтобы установить точку W.

- Измерьте и запишите длину линии VW вдоль касательной.
- Поместите прибор в точку P. Наведите заднюю точку на точку W и отклоните ее под углом 90 градусов к линии PQ, параллельной AV.
- Измерьте вдоль этой линии обзора точку Q за препятствием. Установите точку Q и запишите расстояние PQ.
- Поместите инструмент в точку Q, заднюю точку P и отклоните ее под углом 90 градусов к линии QS. Измерьте вдоль этой линии визирования расстояние QS, равное PW, и установите точку S. Обратите внимание, что номер станции точки S = PI – (линия VW + линия PQ).
- Установите ПК со смещением в точке Y, отмерив от точки Q к точке P расстояние, равное станции ПК минус пикет S. Чтобы установить ПК после удаления препятствия, поместите инструмент в точку Y, заднюю точку Q, отложите угол 90 градусов и расстояние от Y до PC, равное линиям PW и QS. Тщательно установите опорные точки для точек Q, S, Y и W, чтобы убедиться, что точки доступны для установки ПК после расчистки и начала строительства.

Недоступный ПТ
Когда PT недоступен, как показано на рис. 8, а PI и ПК легкодоступны, геодезист должен установить смещенную станцию на PT, используя метод для недоступного ПК со следующими исключениями.
- Обозначьте кривую так, чтобы точка A находилась на PT, а не на PC (см. рис. 8).
- Проложить кривую как можно дальше от ПК вместо ПТ.
- Угол dp — это угол в центре кривой между точкой P и PT, который равен удвоенной разнице между отклонением в точке P и половиной I. Выполните шаги для недоступных PC, чтобы задать линии PQ и КС. Обратите внимание, что пикет в точке S равен вычисленному значению пикета PT плюс YQ.
- Используйте станцию S для нумерации станций выравнивания впереди.
Препятствие на кривой
На некоторых кривых есть препятствия, достаточно большие, чтобы мешать прямой видимости и записи. Обычно затрагиваются только несколько станций. Геодезист не должен тратить слишком много времени на предварительную работу. На рис. 9 показан способ обхода препятствия на кривой.
На рис. 9 показан способ обхода препятствия на кривой.
- Установите прибор над ПК так, чтобы горизонтальный круг находился на 0˚00’, и, если возможно, наведитесь на Check I/2 от PI до PT.
- Установите как можно больше станций на кривой до препятствия, точка b.
- Установите прибор над ПТ пластинами на уровне I/2. Прицел на ИП.
- Назад на как можно большем количестве станций за препятствием, точка e.
- После того, как препятствие устранено, можно установить заблокированные станции c и d.
КРИВАЯ ЧЕРЕЗ ФИКСИРОВАННУЮ ТОЧКУ
Из-за топографических особенностей или других препятствий геодезист может счесть необходимым определить радиус кривой, которая проходит через фиксированную точку или избегает ее и соединяет две заданные прямые. Это может быть выполнено следующим образом (рис. 10):
- Учитывая ТП и угол I из предварительного хода, поместите инструмент на ТП и измерьте угол d так, чтобы угол d был углом между фиксированной точкой и касательной, лежащей на той же стороне кривой как неподвижная точка.

- Измерить линию y, расстояние от PI до фиксированной точки.
- Вычисление углов c, b и a в треугольнике COP.
c = 90 – (d + I/2)
Чтобы найти угол b, сначала решите угол e
Sine e = Sin c/Cos I/2
Угол b = 180°- угол e
a = 180° – (b + c) - Вычислите радиус желаемой кривой, используя формулу
R = y Sin c/Sin a - Вычислите степень кривой до пять знаков после запятой , используя следующие формулы :
(дуговой метод) D = 5729,58 фут/об D = 1746,385 м/об
(хордовый метод) Sin D = 2 (50 футов/об) Sin D = 2 (15,24 м/об) - Вычислить оставшиеся элементы кривую и углы отклонения, и разбейте кривую.
ОГРАНИЧИВАЮЩИЕ ФАКТОРЫ
В некоторых случаях геодезист может использовать элементы, отличные от радиуса, в качестве ограничивающего фактора при определении размера кривой. Обычно это касательная T, внешняя E или средняя ордината M. Когда задается какой-либо ограничивающий фактор, он обычно представляется в виде T, равного некоторому значению x, T ≥ x или T ≤ x. В любом случае первым шагом является определение радиуса по одной из следующих формул:
В любом случае первым шагом является определение радиуса по одной из следующих формул:
Дано: Тангенс; тогда R = T/(Tan ½I)
Внешний; тогда R = E/[(l/Cos ½I) – 1]
Средний ординат; тогда R = M/(l – Cos ½I)
Затем геодезист определяет D. Если ограничивающий фактор представлен в виде T, равном некоторому значению x, геодезист должен вычислить D, провести до пяти знаков после запятой и вычислить остаток кривой. Если представлен ограничивающий фактор ≥, то D округляется в меньшую сторону до ближайшего ½ градуса. Например, если E ≥ 50 футов, геодезист должен округлить до ближайшего ½ градуса, повторно вычислить E и вычислить остальные данные кривой, используя округленное значение D. Новое значение E будет равно или больше, чем 50 футов.
Если ограничивающий фактор ≤, D округляется до ближайшего ½ градуса. Например, если M ≤ 45 футов, то D округляется до ближайшего ½ градуса, M пересчитывается, а остальные данные кривой вычисляются с использованием округленного значения D. Новое значение M будет равно или менее 45 футов.
Новое значение M будет равно или менее 45 футов.
Геодезист может также использовать значения из таблицы A-5 для вычисления значения D. Это делается путем деления табличного значения касательной, внешней или средней ординаты для l-градусной кривой на заданное значение предельного фактор. Например, при предельном касательном T ≤ 45 футов и I = 20°20’, T для 1-градусной кривой из таблицы A-5 составляет 1027,6, а D = 1027,6/45,00 = 22,836°. Округлив до половины градуса, D = 23°. Используйте это округленное значение для пересчета D, T и остальных данных кривой.
СЛОЖНЫЕ КРИВЫЕ
Составная кривая — это две или более простых кривых, которые имеют разные центры, изгибаются в одном направлении,
лежат по одну сторону от их общей касательной и соединяются, образуя непрерывную дугу. Точка, где соединяются две кривые (а именно, точка, в которой PT первой кривой равняется PC второй кривой), называется точкой составной кривизны (PCC).
Поскольку длина касательных к ним различается, составные кривые гораздо лучше соответствуют топографии, чем простые кривые. Эти кривые легко адаптируются к гористой местности или районам, прорезанным большими извилистыми реками. Однако, поскольку составные кривые более опасны, чем простые кривые, их никогда не следует использовать там, где подойдет простая кривая.
Эти кривые легко адаптируются к гористой местности или районам, прорезанным большими извилистыми реками. Однако, поскольку составные кривые более опасны, чем простые кривые, их никогда не следует использовать там, где подойдет простая кривая.
Данные составных кривых
Вычисление составных кривых связано с двумя основными проблемами. Во-первых, составная кривая должна быть проложена между двумя последовательными ТП на предварительном ходе. Во-вторых, кривая должна быть проложена между двумя последовательными касательными на предварительном ходе. (См. рис. 11.)
Составная кривая между последовательными PI
Расчеты и процедура построения составной кривой между последовательными PI описаны в следующих шагах. Эта процедура проиллюстрирована на рисунке 11а.
- Определите PI первой кривой в точке A по полевым данным или предыдущим расчетам.
- Получите I1, I2 и расстояние AB из полевых данных.
- Определите значение D1, D для первой кривой.
 Это может быть вычислено из ограничивающего фактора на основе масштабированного значения из плана дороги или предоставлено инженером проекта.
Это может быть вычислено из ограничивающего фактора на основе масштабированного значения из плана дороги или предоставлено инженером проекта. - Вычислить R1, радиус первой кривой, как показано на страницах с 11 по 13.
- Вычислить T1, тангенс первой кривой.
T1 = R1(Tan ½ I) - Вычислите T2, касательную второй кривой.
T2 = AB – T1 - Вычислите R2, радиус второй кривой.
R2 =T2/Tan ½ I - Вычислите D2 для второй кривой. Поскольку касательная для второй кривой должна быть точной, значение D2 должно быть доведено до пяти знаков после запятой.
- Сравните D1 и D2. Они не должны отличаться более чем на 3 градуса. Если они различаются более чем на 3 градуса, геодезист должен рассмотреть возможность изменения конфигурации кривой.
- Если два D приемлемы, то вычислить оставшиеся данные и углы отклонения для первой кривой.
- Вычислите PI второй кривой. Поскольку PCC находится на той же станции, что и PT первой кривой, то PI2 = PT1 + T2.

- Вычислите оставшиеся данные и углы отклонения для второй кривой и наложите кривые.
Составная кривая между последовательными касательными. Следующие шаги объясняют построение составной кривой между последовательными касательными. Эта процедура показана на рисунке 11b.
- Определите угол PI и I по полевым данным и/или предыдущим расчетам.
- Определите значение I1 и расстояние AB. Геодезист может сделать это с помощью полевых измерений или масштабирования расстояния и угла по плану и профильному листу.
- Вычислить угол C.
C = 180 – I - Вычислить I2.
I2 =180-(Il+C) - Вычислить строку AC.
AC = AB Sin I2/Sin C - Вычислить строку BC.
BC = AB Sin I1/Sin C - Вычислите станцию PI1.
PI1 = PI – AC - Определите D1 и рассчитайте R1 и T1 для первой кривой, как описано на страницах с 11 по 13.
- Рассчитайте T2 и R2, как описано на страницах с 11 по 13.

- Рассчитайте D2 в соответствии с формулами на страницах с 11 по 13.
- Расчет станции на ПК.
PC1 = PI – (AC + T1) - Вычислите остальные данные кривой и углы отклонения для первой кривой.
- Вычислить PI2.
PI2 = PT1 + T2 - Вычислите оставшиеся данные кривой и углы отклонения для второй кривой и разбейте кривые.
Разбивка составных кривых
При разбивке кривой в поле необходимо соблюдать осторожность. Описаны две процедуры разбивки составных кривых.
Составная кривая между последовательными PI. Разметьте первую кривую, как описано на стр. 14 и 15.
- Проверьте PCC и PT2, поместив инструмент на PCC, наведя на PI2 и отложив I2/2. Полученная линия прямой видимости должна пересекать PT2.
- Разбейте вторую кривую так же, как и первую.
Составная кривая между последовательными касательными. Поместите инструмент на PI и наведитесь на заднюю касательную.
- Разметьте расстояние AC от ТП вдоль задней касательной и установите ТП1.
- Продолжайте движение по обратной касательной от PI2 на расстояние T1 и установите PC1.
- Визируйте по прямой касательной, когда инструмент все еще находится в PI.
- Разметьте расстояние до н.э. от ТП вдоль прямой касательной и установите ТП2. 906:00 Продолжайте движение по прямой касательной от PI на расстояние T2 и установите PT2.
- Проверьте местоположение PI1 и PI2, либо измерив расстояние между двумя PI и сравнив измеренное расстояние с вычисленной длиной линии AB, либо поместив инструмент в PI1, наведя PI и отложив I1. Полученная линия прямой видимости должна пересекать PI2.
- Разметьте кривые, как описано на страницах 14 и 15.
ОБРАТНЫЕ КРИВЫЕ
Обратная кривая состоит из двух или более простых кривых, поворачивающихся в противоположных направлениях. Их точки пересечения лежат на противоположных концах общей касательной, а ПТ первой кривой совпадает с ПК второй. Эта точка называется точкой обратной кривизны (PRC).
Эта точка называется точкой обратной кривизны (PRC).
Обратные кривые полезны при разметке таких объектов, как трубопроводы, лотки и дамбы. Геодезист также может использовать их на низкоскоростных дорогах и железных дорогах. Их нельзя использовать на высокоскоростных дорогах или железных дорогах, поскольку они не могут быть должным образом подняты на вираж в КНР. Их иногда используют на каналах, но только с особой осторожностью, так как они затрудняют навигацию по каналу и способствуют эрозии.
Данные кривой обратного хода
Вычисление кривых обратного хода связано с тремя основными проблемами. Во-первых, обратная кривая должна быть проложена между двумя последовательными PI. (См. рис. 12.) В этом случае геодезист выполняет вычисления точно так же, как составная кривая между последовательными PI. Во-вторых, кривая должна быть проложена так, чтобы она соединяла две параллельные прямые (рис. 13). Третья проблема заключается в том, где нужно провести обратную кривую так, чтобы она соединяла расходящиеся касательные (рис. 14).
14).
Соединение параллельных прямых
На рис. 13 показана обратная кривая, соединяющая две параллельные прямые. ПК и ПТ расположены следующим образом.
- Измерьте p, перпендикулярное расстояние между касательными.
- Найдите PRC и измерьте m1 и m2. (Если позволяют условия, PRC может находиться в средней точке между двумя касательными. Это уменьшит объем вычислений, поскольку обе дуги будут идентичными.)
- Определите R1.
- Вычисление I1.
- Вычислить L1 из
L1 = R1 Sin I1
R2 , I2 и L2 определяются так же, как R1, I1 и L1. Если PRC должна быть средней точкой, значения для дуги 2 будут такими же, как и для дуги 1. - Разбейте каждую из дуг так же, как простую кривую. При необходимости геодезист может легко определить другие компоненты кривой. Например, геодезисту нужна обратная кривая для соединения двух параллельных прямых. Никаких препятствий не существует, поэтому его можно составить из двух равных дуг.
 Степень изгиба для обоих должна быть 5°. Геодезист измеряет расстояние p и находит его равным 225,00 футам.
Степень изгиба для обоих должна быть 5°. Геодезист измеряет расстояние p и находит его равным 225,00 футам.
m1 = m2 и L1= L2 R1= R2 и I1= I2 - PC и PT находятся путем измерения L1 и L2.
Соединение расходящихся прямых
Соединение двух расходящихся прямых обратной кривой показано на рис. 14. Из-за возможных препятствий или топографических соображений нельзя использовать одну простую кривую между прямыми. PT был перемещен обратно за пределы PI. Однако угол I все еще существует, как и в простой кривой. Управляющими размерами на этой кривой являются расстояние Ts до местоположения PT и значения R1 и R2, которые вычисляются на основе заданной степени кривой для каждой дуги.
- Мера I в PI.
- Измерьте Ts, чтобы найти PT как точку, в которой кривая должна соединиться с прямой касательной. В некоторых случаях будет указано положение PT, но для расчетов все же необходимо измерить Ts.
- Выполните следующие расчеты:
Определите R и R . Если возможно, пусть R равно R.
Если возможно, пусть R равно R.
Угол s = 180-(90+I)=90-I
m = Ts (Tan I)
угол e = I1 (для подобных треугольников) угол f = I1 (для подобных треугольников) следовательно, I2 = I + I1
n = (R2 – m) Sin e p = (R2 – m) Cos e
Определите g, установив значение I1. Зная Cos I1, определите Sin I1.
g = (R1+ R2) Sin I1
TL = g + n + L - Измерьте TL от PI, чтобы найти ПК.
- Разметить дугу 1 в PRC с ПК.
- Установите инструмент на PT и проверьте PRC (переверните зрительную трубу, наведитесь на PI, погрузитесь и поверните на угол I2/2).
- Закрепить дугу 2 до КНР от ПТ.
Например, на рис. 14 обратная кривая соединяет две расходящиеся касательные, причем обе дуги имеют кривую 5 градусов. Геодезист находит PI и измеряет угол I как 41 градус. Местоположение PT указывается, а Ts измеряется как 550 футов.
ПК находится путем измерения T . Кривая разбивается с использованием вычислений 5-градусной кривой.
СПИРАЛЬНЫЕ КРИВЫЕ
В инженерном строительстве геодезист часто вставляет переходную кривую, также известную как спиральная кривая, между круговой кривой и касательной к этой кривой. Спираль — это кривая переменного радиуса, используемая для постепенного увеличения кривизны дороги или железной дороги. Спиральные кривые используются в основном для уменьшения заноса и затруднений при управлении путем постепенного перехода от прямолинейного движения к повороту и/или для обеспечения метода адекватного подъема кривых.
Спиральная кривая предназначена для обеспечения постепенного подъема внешнего края тротуара дороги для противодействия центробежной силе транспортных средств при их прохождении. Наилучшей спиральной кривой является та, в которой вираж увеличивается равномерно с увеличением длины спирали от TS или точки, где спиральная кривая выходит из касательной.
Кривизна спирали должна равномерно увеличиваться от начала до конца. В начале, где она выходит из касательной, ее кривизна равна нулю; в конце, где он соединяется с круговой кривой, он имеет ту же степень кривизны, что и круговая кривая, которую он пересекает.
Теория А.Р.Е.А. 10-Chord Spiral
Спираль Американской ассоциации инженеров железнодорожного транспорта, известная как A.R.E.A. спираль, сохраняет почти все характеристики кубической спирали. В кубической спирали длины считались измеренными вдоль самой спиральной кривой, но измерения в поле должны производиться по хордам. Признавая этот факт, в A.R.E.A. спираль длина спирали измеряется 10 равными хордами, так что теоретическая кривая
приведена в соответствие с полевой практикой. Эта спираль из 10 хорд очень близка к кубической спирали. В основном две кривые совпадают до точки, где Δ = 15 градусов. Точные формулы для этого A.R.E.A. 10-хордовая спираль, когда Δ не превышает 45 градусов, приведены на стр. 28 и 29.
Спиральные элементы
На рисунках 15 и 16 показаны обозначения, применяемые к элементам простой круговой кривой со спиралями, соединяющими ее с касательными.
TS = точка перехода от тангенса к спирали
SC = точка перехода от спирали к круговой кривой CS = точка перехода от круглой кривой к спирали ST = точка перехода от спирали к касательной
SS = точка перехода с одной спирали на другую (не показана на рис. 15 и 16)
15 и 16)
Символы PC и PT, TS и ST, SC и CS транспонируются при изменении направления пикетирования.
a = угол между касательной в TS и хордой от TS до любой точки спирали
A = угол между касательной в TS и хордой от TS до SC
b = угол угол в любой точке спирали между касательной в этой точке и хордой из TS
B = угол в SC между хордой из TS и касательной в SC
c = хорда от любой точки спирали до TS C = хорда от TS до SC
d = степень кривой в любой точке спирали D = степень кривой дуги окружности
f = угол между любой хордой спирали (рассчитывается при необходимости) и касательной через ТС
I = угол отклонения между начальной и конечной касательными; общий центральный угол круговой кривой и спирали
k = увеличение степени кривой на станцию на спирали
L = длина спирали в футах от TS до любой заданной точки спирали
Ls = длина спирали в футах от TS до SC, измеренная в 10 равных хордах
o = ордината офсетного ПК; расстояние между касательной и параллельной касательной к смещенной кривой
r = радиус соприкасающейся окружности в любой данной точке спирали
R = радиус центральной круговой кривой
s = длина спирали на станциях от ТС до любой заданной точки
S = длина спирали в станциях от TS до SC
u = расстояние по касательной от TS до пересечения с касательной через любую заданную точку спирали
U = расстояние по касательная от ТС до пересечения с касательной через СК; более длинная спиральная касательная
v = расстояние по касательной через любую заданную точку от этой точки до пересечения с касательной через TS
V = расстояние по касательной через SC от SC до пересечения с касательной через ТС; более короткая спиральная касательная
x = расстояние по касательной от TS до любой точки спирали
X = расстояние по касательной от TS до SC y = смещение по касательной любой точки на спирали Y = смещение по касательной к SC
Z = расстояние по касательной от TS до смещенного PC (Z = X/2, приблизительно)
8 = центральный угол спирали от TS до любой заданной точки
Δ = центральный угол всей спирали
Ts = расстояние касательной спиральной кривой; расстояние от TS до PI, точка пересечения касательных
Es = внешнее расстояние смещенной кривой
Формулы спирали
Следующие формулы предназначены для точного определения функций 10-хордовой спирали, когда центральный угол Δ не превышает 45 градусов. Они подходят для составления таблиц и точной полевой работы.
Они подходят для составления таблиц и точной полевой работы.
Эмпирические формулы
Для использования в полевых условиях следующие формулы достаточно точны для практических целей, когда Δ не превышает 15 градусов.
a = o/3 (градусы)
A = Δ/3 (градусы)
a = 10 ks2 (минуты)
S = 10 ks2 (минуты)
Длина спирали
При расчете необходимо учитывать различные факторы отрезки спирали для прокладки автомобильных и железных дорог.
Автомобильные дороги. Спирали, применяемые для разметки шоссе,
должны быть достаточно длинными, чтобы можно было в достаточной мере компенсировать влияние центробежной силы за счет надлежащего виража. Минимальная переходная длина спирали для любой степени кривизны и расчетной скорости получается из соотношения Ls = 1,6V3/R, в котором Ls — минимальная длина спирали в футах, V — расчетная скорость в милях в час, а R — радиус кривизны простой кривой. Это уравнение не является математически точным, а является приблизительным, основанным на многолетних наблюдениях и дорожных испытаниях.
Таблица 1 составлена из приведенного выше уравнения для значений, кратных 50 футам. Когда спирали вставляются между дугами составной кривой, используйте Ls = 1,6V3/Ra. Ra представляет собой радиус кривой в градусах, равных разности степеней кривизны дуг окружности.
Железные дороги Спирали, применяемые для разметки железных дорог, должны быть достаточно длинными, чтобы обеспечить увеличение виража не более чем на 1¼ дюйма в секунду для достижения максимальной скорости движения поезда. Минимальная длина определяется из уравнения Ls = 1,17 EV. E — полный теоретический вираж кривой в дюймах, V — скорость в милях в час, а Ls — длина спирали в футах.
Эта длина спирали обеспечивает наилучшие условия для катания, поддерживая желаемое соотношение между величиной виража и степенью кривизны. Степень кривизны увеличивается равномерно по всей длине спирали. Это же уравнение используется для вычисления длины спирали между дугами составной кривой. В таком случае E представляет собой разницу между виражами двух дуг окружности.
В таком случае E представляет собой разницу между виражами двух дуг окружности.
СПИРАЛЬНЫЕ РАСЧЕТЫ
Спиральные элементы легко вычисляются по формулам, приведенным на страницах 26 и 27. Чтобы использовать эти формулы, должны быть известны определенные данные. Эти данные обычно получают из планов местоположения или полевых измерений.
Следующие вычисления относятся к спирали, когда известны D, V, точка PI и I.
D = 4°
I = 24°10′
Пикет PI = 42 + 61,70
V = 60 миль/ч
Определение Δ
Определение o
Определение Z
Определение TS
Определение длины хорды
Определение значений станции
С приведенными выше данных приведенные выше точки кривой рассчитываются следующим образом:
Определение углов отклонения
Основные. спираль заключается в том, что углы отклонения изменяются пропорционально квадрату расстояния вдоль кривой.
спираль заключается в том, что углы отклонения изменяются пропорционально квадрату расстояния вдоль кривой.
Из этого уравнения получаются следующие соотношения:
Углы отклонения к различным точкам спирали от TS или ST составляют a1, a2, a3. . . а9 и а10. Используя эти соотношения, углы отклонения спиралей и дуги окружности вычисляются для примера спиральной кривой.
Страница 21 утверждает, что.
СХЕМА СПИРАЛЬНОЙ КРИВОЙ
Ниже описана процедура построения спиральной кривой с использованием одноминутного прибора с горизонтальным кругом, который считывается вправо. Рисунок 17 иллюстрирует эту процедуру.
Настройка TS и ST
Когда инструмент находится в точке PI, оператор визирует по задней касательной и удерживает головку рулетщика на линии, пока измеряется расстояние по касательной (Ts). Ставка устанавливается на линии и помечается, чтобы показать TS и его значение станции.
Приборщик теперь наведется вдоль прямой касательной, чтобы измерить и установить ST.
Разметка первой спирали от TS до SC
Установите инструмент на TS, указывая на PI, с 0°00’ на горизонтальной окружности.
- Проверьте угол к ST, если это возможно. Угол должен быть равен половине угла I, если TS и ST расположены правильно.
- Первое отклонение (a1/0˚01’) вычитается из 360 градусов, а остаток устанавливается на горизонтальной окружности. Измерьте стандартную длину хорды спирали (25 футов) от TS и установите первую спиральную станцию (38 + 54,66) на линии.
- Остальные спиральные станции устанавливаются путем вычитания их углов отклонения из 360 градусов и измерения 25 футов от ранее установленной станции.
Разметка дуги окружности от SC до CS
Установите инструмент на SC со значением A минус A (5° 00’- 1°40’ = 3° 20’) на горизонтальной окружности. Наведитесь на ТС, установив зрительную трубу в обратном положении.
- Погрузите телескоп. Вращайте зрительную трубу до тех пор, пока на горизонтальном круге не появится 0° 00’.
 Теперь инструмент наведен по касательной к дуге окружности в точке SC.
Теперь инструмент наведен по касательной к дуге окружности в точке SC. - Первое отклонение (dl/0° 24’) вычитается из 360 градусов, а остаток устанавливается на горизонтальной окружности. Первая подхорда (c1 / 20,34 фута) измеряется от SC, и на линии устанавливается кол и отмечается пикет 41+00.
- Остальные пикеты дуги окружности устанавливаются путем вычитания их углов отклонения из 360 градусов и измерения соответствующего расстояния по хорде от ранее установленного пикета.
Разметка второй спирали от ST к CS
Установите инструмент на ST, указывая на PI, с 0° 00’ на горизонтальной окружности.
- Проверить угол на CS. Угол должен быть равен 1° 40’, если CS расположена правильно.
- Установите спиральные станции, используя их углы отклонения в обратном порядке и стандартную длину спирального хорда (25 футов).
Исправьте любую обнаруженную ошибку, отрегулировав хорды дуги окружности от SC к CS.
Промежуточная настройка
Когда инструмент необходимо переместить в промежуточную точку на спирали, углы отклонения, рассчитанные по TS, нельзя использовать для остальной части спирали. В этом отношении спираль отличается от круговой кривой.
В этом отношении спираль отличается от круговой кривой.
Расчет углов отклонения Ниже приведены процедуры расчета углов отклонения и разбивки спирали.
Пример:
D= 4°
Ls = 250 футов (для шоссе)
V = 60 миль/ч
I = 24° 10’
Точка 5 = промежуточная точка
- Рассчитайте углы отклонения для первых пяти точек. Эти углы равны: a1 = 0° 01’, a2 = 0° 04’, a3 = 0° 09’, a4 = 0° 16’ и a5 = 0° 25’.
- Углы отклонения для точек 6, 7, 8, 9 и 10 при приборе в точке 5 рассчитывают с использованием таблицы 2. Таблица 2 читается следующим образом: при приборе в любой точке коэффициенты полученные, которые при умножении на a1 дают углы отклонения к другим точкам спирали. Следовательно, при приборе в точке 5 коэффициенты для точек 6, 7, 8, 9, и 10 равны 16, 34, 54, 76 и 100 соответственно.
Умножьте эти коэффициенты на a1, чтобы получить
ФУНКЦИИ И ТИПЫ
При пересечении двух линий уклона происходит вертикальное изменение направления. Чтобы обеспечить безопасное и комфортное путешествие, геодезист закругляет пересечение, вставляя вертикальную параболическую кривую. Параболическая кривая обеспечивает постепенное изменение направления от одного класса к другому.
Чтобы обеспечить безопасное и комфортное путешествие, геодезист закругляет пересечение, вставляя вертикальную параболическую кривую. Параболическая кривая обеспечивает постепенное изменение направления от одного класса к другому.
Вертикальная кривая, соединяющая нисходящий уклон с восходящим уклоном или с уклоном менее резко, называется прогибом или перевернутой кривой. Восходящий уровень, за которым следует нисходящий уровень, или один восходящий менее резкий, соединяется вершиной или открытой кривой.
РАСЧЕТЫ
Чтобы добиться плавного изменения направления при прокладке вертикальных кривых, уклон должен подниматься через серию подъемов. Геодезист обычно определяет отметку для вертикальных кривых в начале (точка вертикальной кривизны или PVC), в конце (точка вертикального касания или PVT) и на всех полных станциях. Иногда геодезист может захотеть получить дополнительные баллы, но это будет зависеть от строительных требований.
Длина кривой
Отметки представляют собой вертикальные смещения касательной и отметок (прямолинейный расчетный уклон). Оценки G1 и G2 даны в процентах подъема на 100 футов горизонтального расстояния. Геодезист определяет оценки как положительные или отрицательные, в зависимости от того, являются ли они возрастающими или нисходящими в направлении обследования. Длина вертикальной кривой (L) представляет собой горизонтальное расстояние (в 100-футовых станциях) от PVC до PVT. Обычно кривая простирается на ½ L станций с каждой стороны от точки вертикального пересечения (PVI) и наиболее удобно делится на полные приращения станций.
Оценки G1 и G2 даны в процентах подъема на 100 футов горизонтального расстояния. Геодезист определяет оценки как положительные или отрицательные, в зависимости от того, являются ли они возрастающими или нисходящими в направлении обследования. Длина вертикальной кривой (L) представляет собой горизонтальное расстояние (в 100-футовых станциях) от PVC до PVT. Обычно кривая простирается на ½ L станций с каждой стороны от точки вертикального пересечения (PVI) и наиболее удобно делится на полные приращения станций.
Кривая провисания показана на рис. 20. Геодезист может получить данные кривой следующим образом (где BV и CV являются соединяемыми линиями уклона).
Определить значения G1 и G2, исходные сорта. Чтобы получить минимальную длину кривой (L) на станциях, разделите алгебраическую разность G1 и G2 (AG) на скорость изменения (r), которая обычно включается в критерии проектирования. Если скорость изменения (r) не указана, используйте следующие формулы для вычисления L:
Если L не выходит из этой формулы на целое число станций, оно обычно расширяется до ближайшего целого числа. Обратите внимание, что это снижает скорость изменений. Таким образом, L = 4,8 станций будет расширено до 5 станций, а значение r будет вычислено из r = Δ G/L. Эти формулы предназначены только для проектирования дорог. Геодезист должен использовать разные формулы для проектирования железных дорог и аэродромов.
Обратите внимание, что это снижает скорость изменений. Таким образом, L = 4,8 станций будет расширено до 5 станций, а значение r будет вычислено из r = Δ G/L. Эти формулы предназначены только для проектирования дорог. Геодезист должен использовать разные формулы для проектирования железных дорог и аэродромов.
Интервал станций
После определения длины кривой геодезист выбирает соответствующий интервал станций (SI). Первый фактор, на который следует обратить внимание, — это рельеф. Чем неровнее рельеф, тем меньше интервал между станциями. Второе соображение заключается в выборе интервала, который поместит станцию в центр кривой с одинаковым количеством станций по обеим сторонам кривой. Например, 300-футовую кривую нельзя разбить с интервалом в 100 футов, но можно разбить с интервалом в 10, 25, 30, 50 или 75 футов. Геодезист часто использует те же интервалы, что и рекомендуемые для горизонтальных кривых, то есть 10, 25, 50 и 100 футов.
Поскольку PVI является единственной фиксированной станцией, следующим шагом будет вычисление значения станции для PVC, PVT и всех станций на кривой.
PVC = PVI – L/2
PVT = PVI + L/2
Другие станции определяются, начиная с PVI, добавляя SI и продолжая до тех пор, пока не будет достигнуто PVT.
Отметки по касательной
Вычислить отметки по касательной PVC, PVT и всех пикетов вдоль кривой. Поскольку PVI является фиксированной точкой касательной, геодезист вычисляет высоты станции следующим образом:
Отметка PVC = Отметка PVI + (-1 x L/2 x G1)
Отметка PVT = Отметка PVI + (L/2 x G2)
Геодезист может найти высоту станций вдоль обратной касательной следующим образом:
Высота стационара = Высота ПВХ + (расстояние от ПВХ x G1).
Превышение пикетов по прямой касательной находится следующим образом:
Отметка станции = Отметка PVI + (расстояние от PVI x G2)
Вертикальный максимум
PVI и середина хорды, проведенной между PVC и PVT. На рисунке 19, линия VE = DE и называется вертикальным максимумом (Vm). Значение Vm вычисляется следующим образом: (L = длина в 100-футовых станциях. На 600-футовой кривой L = 6.)
На 600-футовой кривой L = 6.)
На практике геодезист должен вычислить значение Vm, используя обе формулы, поскольку Работа обоих обеспечивает проверку Vm, возвышения PVC и возвышения PVT.
Вертикальное смещение. Значение смещения по вертикали — это расстояние между касательной и уклоном дороги. Это значение зависит от квадрата расстояния от PVC или PVT и рассчитывается по формуле:
Смещение по вертикали = (Расстояние)2 x Vm
Параболическая кривая представляет собой зеркальное отображение. Это означает, что вторая половина кривой идентична первой половине, а смещения одинаковы для обеих сторон кривой.
Высота станции. Затем геодезист вычисляет отметку уклона дороги на каждой станции вдоль кривой. Отметка кривой на любом пикете равна отметке касательной на этом пикете плюс или минус вертикальное смещение для этого пикета. Знак смещения зависит от знака Vm (плюс для кривой прогиба и минус для кривой вершины). ).
).
Первое и второе отличия. На последнем этапе геодезист определяет значения первой и второй разностей. Первые разности — это разности высот между последовательными станциями вдоль кривой, а именно: высота второй станции минус высота первой станции, высота третьей станции минус высота второй и т. д. Вторые разности — это разности между разностями высот (первые разности), и они вычисляются в той же последовательности, что и первые разности.
Геодезист должен очень внимательно наблюдать и записывать алгебраический знак как первой, так и второй разности. Вторые разности обеспечивают проверку скорости изменения на станцию вдоль кривой и проверку вычислений. Все вторые разности должны быть равны. Однако они могут отличаться на один или два в последнем десятичном разряде из-за округления при вычислениях. Когда это произойдет, они должны сформировать узор. Если они слишком сильно различаются и/или не образуют закономерности, геодезист допустил ошибку в расчетах.
Пример: вертикальная кривая соединяет линии уклона G1 и G2 (рис. 19). Максимально допустимый уклон (r) составляет 2,5 процента. Оценки G1 и G2 составляют -10 и +5.
Вертикальные смещения для каждой станции рассчитываются, как показано на рисунке 20. Первая и вторая разности определяются в качестве проверки. На рисунке 21 показано решение кривой вершины со смещением для 50-футовых интервалов.
Верхние и нижние точки
Геодезист использует верхнюю или нижнюю точку вертикальной кривой, чтобы определить направление и количество стока, в случае вершинных кривых, и найти нижнюю точку для дренажа.
Если уклоны равны, верхняя или нижняя точка будет находиться в центре кривой. Когда оба угла наклона плюсовые, нижняя точка находится в PVC, а верхняя точка в PVT. Когда оба уклона тангенса отрицательные, верхняя точка находится в PVC, а нижняя точка в PVT. Когда встречаются неравные положительные и отрицательные тангенциальные уклоны, верхняя или нижняя точка будет находиться на той стороне кривой, которая имеет более пологий уклон.
Расстояние по горизонтали. Геодезист определяет расстояние (x, выраженное в станциях) между PVC или PVT и верхней или нижней точкой по следующей формуле:
G — более плоский из двух градиентов, а L — количество станций кривой.
Расстояние по вертикали. Геодезист вычисляет разницу высот (y) между PVC или PVT и верхней или нижней точкой по формуле
Пример: Из кривой на рисунке 21 G1= + 3,2%, G2 = – 1,6% L = 4 (400). Поскольку G2 является более плоским градиентом, верхняя точка будет находиться между PVI и PVT.
Угловые векторные силы — канатная книга
Угловые векторные силы возникают, когда канаты проходят через отклонение или направляющий шкив. В зависимости от созданного угла это может иметь многократное влияние на силы, которые ощущаются на компонентах отклоняющего или направленного шкива и связанных с ними опорных точках.
Сила — это воздействие, которое имеет как величину, так и направление, обычно выражается в динамических единицах Ньютонов (Н). Для простоты объяснения мы использовали килограммы на этой странице.
Для простоты объяснения мы использовали килограммы на этой странице.
Основы
Здесь у нас груз весом 100 кг. Веревка была прикреплена к грузу, а затем пропущена через направляющий шкив, который возвращает веревку обратно к пользователю на уровне земли. Две части веревки параллельны друг другу, поэтому нет внутреннего или внутреннего угла.
В этой ситуации направляющий шкив и его точка крепления фактически нагружаются 200 кг, так как с одной стороны находится вес груза, а с другой стороны пользователь прикладывает усилие в 100 кг, чтобы удержать груз на месте .
Система шкива перенаправления 1:1Угол отклонения 20°
Здесь канат отклонился от своей первоначальной линии (на этом рисунке от вертикали) на 20°. В то время как весь вес нагрузки приходится на основную точку крепления, часть веса нагрузки также прикладывается к компонентам отклоняющего/направленного шкива.
При отклонении в 20° 34% веса нагрузки будет прикладываться к точке крепления отклоняющего/направленного шкива. В этой ситуации, когда у нас есть нагрузка 100 кг, это создаст силу 34 кг на отклоняющем / направленном шкиве.
В этой ситуации, когда у нас есть нагрузка 100 кг, это создаст силу 34 кг на отклоняющем / направленном шкиве.
Угол отклонения 45°
По мере увеличения угла отклонения сила, действующая на анкер отклоняющего или направленного шкива, также увеличивается. Угол отклонения, равный 45°, будет создавать усилие на опорной точке отклонения, эквивалентное 76% веса груза, поэтому в этом примере, когда груз весит 100 кг, это будет 76 кг.
Угол отклонения 45°Угол отклонения 60°
При угле отклонения 60° 100% веса нагрузки будет прикладываться к точке крепления отклонения или направляющего шкива.
Это можно сравнить с критическим углом, найденным в векторных силах, когда такелаж y висит, так как все три угла равны.
Угол отклонения 60°Угол отклонения 90°
Угол отклонения 90° приводит к тому, что сила, равная 141% веса груза, прикладывается к точке отклонения или опорной точке направляющего шкива.
Обратите внимание, что это также будет одинаковой нагрузкой для прилежащего угла 90°, поскольку они оба одинаковы.
Угол отклонения 90°Угол отклонения: Расчеты
Угловой Векторные силы можно рассчитать с помощью математической формулы. Вот формула, которую мы можем использовать для расчета силы, прикладываемой к отклонению или опорной точке направляющего шкива при измерении угла отклонения.
До сих пор на этой странице мы использовали килограммы для обозначения нагрузок на иллюстрациях. Поскольку килограмм является единицей измерения массы, его следует преобразовать в вес (ньютоны), чтобы правильно рассчитать результирующую силу.
Где:
F результирующая сила, действующая на точку крепления отклонения или направляющего шкива.
w вес груза.
α — это угол, на который веревка отклонилась от своей первоначальной линии.
Угол отклонения: использование процентного коэффициента
Процентный коэффициент можно использовать для расчета величины силы, приложенной к точке крепления отклонения или направляющего шкива. Этого можно добиться, используя следующую формулу:
Этого можно добиться, используя следующую формулу:
| Angle | % factor | Angle | % factor | Angle | % factor |
|---|---|---|---|---|---|
| 0° | 0.0 | 65° | 107.5 | 130° | 181.3 |
| 5° | 8.7 | 70° | 114.7 | 135° | 184.8 |
| 10° | 17.4 | 75° | 121.7 | 140° | 187.9 |
| 15° | 26.1 | 80° | 128.6 | 145° | 190.7 |
| 20° | 34.7 | 85° | 135.1 | 150° | 193.2 |
| 25° | 43.3 | 90° | 141.4 | 155° | 195.3 |
| 30° | 51. 8 8 | 95° | 147.4 | 160° | 197.0 |
| 35° | 60.1 | 100° | 153.2 | 165° | 198.3 |
| 40° | 68.4 | 105° | 158.7 | 170° | 199.2 |
| 45° | 76.5 | 110° | 163.8 | 175° | 199.8 |
| 50° | 84.5 | 115° | 168.8 | 180° | 200.0 |
| 55° | 92.3 | 120° | 173.2 | ||
| 60° | 100.0 | 125° | 177.4 |
Глядя на это под другим углом
Мы можем измерить угол отклонения или направленного шкива двумя различными способами, который из них наиболее простой и более подходящий для конкретной установки. Здесь мы подробно описали оба метода; измерение от угла отклонения и измерение от прилежащего угла.
Здесь мы подробно описали оба метода; измерение от угла отклонения и измерение от прилежащего угла.
Угол отклонения — это мера того, на сколько градусов веревка отклонилась или отклонилась от своей первоначальной линии. Эти углы будет легче оценить при использовании малых отклонений.
Измерение угловых векторных силПрилежащий угол измеряется между участком каната, который проходит через отклоняющий или направляющий шкив. Обычно легче рассчитать этот тип угловой векторной силы при использовании систем шкивов и высоких перенаправлений.
При измерении отклонений или направленных шкивов прибавленный угол и угол отклонения всегда должны давать 180°.
Прилежащий угол 75°
В этой ситуации мы измерили прилежащий угол между отрезком каната, который проходит вокруг шкива.
Прилагаемый угол составляет 75°, это создаст усилие на направляющем шкиве или отклонение, эквивалентное 159% веса груза. Так что в этом примере это 159 кг!
Включенный угол 75°Прилежащий угол 60°
Мы снова измерили прилежащий угол, образованный в месте прохождения каната через направляющий шкив или отклонение.
При включенном угле 60° к направляющему шкиву или отклонению будет приложена сила, эквивалентная 173% веса груза.
Включенный угол 60°Прилежащий угол 45°
На этом рисунке прилежащий угол равен 45°. Когда прилежащий угол, создаваемый канатом, проходящим через шкив или отклонение, уменьшается до 0°, сила, приложенная к направленному шкиву или отклонению, увеличивается.
В этом примере приложенная сила будет примерно равна 185% веса груза.
Включенный угол 45°Включенный угол: расчеты
Угловые Векторные силы можно рассчитать с помощью математической формулы. Вот формула, которую мы можем использовать для расчета силы, приложенной к отклонению или опорной точке направляющего шкива при измерении от прилежащего угла.
До сих пор на этой странице мы использовали килограммы для обозначения нагрузок на иллюстрациях. Поскольку килограмм является единицей измерения массы, его следует преобразовать в вес (ньютоны), чтобы правильно рассчитать результирующую силу.
Где:
F результирующая сила, действующая на точку крепления отклонения или направляющего шкива.
w вес груза.
α — это угол, на который веревка отклонилась от своей первоначальной линии.
Включенный угол: использование процентного коэффициента
Процентный коэффициент можно использовать для расчета величины силы, прикладываемой к точке крепления отклоняющего/направленного шкива. Этого можно добиться, используя следующую формулу:

 Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).
Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).

 13330.2011;
13330.2011; Возможность учёта развития пластических деформаций задаётя пользователем в параметрах конструирования. При этом можно руководствоваться разд. 8.1. Следует отметить, что в настоящей редакции СП 16.13330.2011, в связи с отсутствием коэффициентов учёта пластики для полного пластического шарнира, конструкции 3 класса по виду напряжённого состояния (полный пластический шарнир) считаются так же, как и конструкции 2 класса (ограниченное развитие пластики).
Возможность учёта развития пластических деформаций задаётя пользователем в параметрах конструирования. При этом можно руководствоваться разд. 8.1. Следует отметить, что в настоящей редакции СП 16.13330.2011, в связи с отсутствием коэффициентов учёта пластики для полного пластического шарнира, конструкции 3 класса по виду напряжённого состояния (полный пластический шарнир) считаются так же, как и конструкции 2 класса (ограниченное развитие пластики).