МУ расчет плоских ферм
Министерство науки и образования Российской Федерации Федеральное агентство по образованию Государственное образовательное учреждение
высшего профессионального образования «Ростовский государственный строительный университет»
Утверждено на заседании кафедры теоретической механики 23 ноября 2005 г.
РАСЧЕТ ПЛОСКИХ ФЕРМ
Методические указания и контрольные задания для студентов заочного отделения
Ростов – на – Дону
2006
2
УДК 531.01
Расчет плоских ферм: Методические указания и контрольные задания для студентов заочного отделения.- Ростов–на-Дону: Рост. гос. строит. ун -т, 2006 — 23 с.
Предназначены для студентов заочного отделения всех специальностей. Приводятся различные методы расчета плоских ферм и разбираются решения типовых примеров.
Составители: Т.В.Виленская С.С.Савченкова
Рецензент: npoф. И.Ф.Хрджиянц
Редактор Н.Е.Гладких Темплан 2006 г., поз. 171
Подписано в печать 24.05.06. Формат 60х84/16. Бумага писчая. Ризограф. Уч.-изд. л.. 1,4. Тираж 100 экз. Заказ Редакционно – издательский центр РГСУ
344022, Ростов н/Д, ул. Социалистическая, 162
© Ростовский государственный строительный университет, 2006
3
ВВЕДЕНИЕ
При постройке мостов, подъемных кранов и других сооружений применяются конструкции, называемые фермами.
Фермой называется конструкция, состоящая из стержней, соединённых между собой на концах шарнирами и образующих геометрически неизменяемую систему.
Шарнирные соединения стержней фермы называют её узлами. Если оси всех стержней фермы лежат в одной плоскости, то ферма называется плоской.
Мы будем рассматривать только плоские фермы. Предполагаем, что выполняются следующие условия:
1)все стержни фермы прямолинейные;
2)трение в шарнирах отсутствует;
3)все заданные силы приложены только в узлах фермы;
4)весом стержней можно пренебречь.
В этом случае каждый стержень фермы находится под действием только двух сил, которые будут вызывать его растяжение или сжатие.
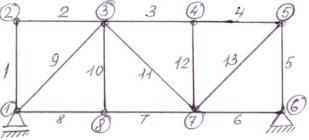
Пусть ферма имеет «m» стержней и «n» узлов. Найдём зависимость между m и n, обеспечивающую жесткость конструкции ( рис. 1 ).
m — 3 = 2-(n-3)
или m = 2n-3. ( 1 )
Если m < 2n — 3, то конструкция не будет геометрически неизменяемой, если m > 2n — 3, ферма будет иметь «лишний» стержень.
Равенство ( 1 ) называется условием жесткости.
Ферма, изображенная на рис. 1 , является жесткой конструкцией
n=8 m= 13
13=8 · 2-3
Рис. 1 Расчёт фермы сводится к определению опорных реакций и усилий в
стержнях, то есть сил, действующих со стороны узлов на примыкающие к нему стержни.
Выясним, при каком соотношении между числом стержней и узлов ферма будет статически определимой. Если все неизвестные силы можно определить из уравнений равновесия, то есть количество независимых уравнений равно числу неизвестных, то конструкция статически определима.
4
Так как на каждый узел фермы действует плоская система сходящихся сил, то всегда можно составить 2n уравнений равновесия. Общее количество неизвестных — m + 3, (где m усилий в стержнях и 3 опорные реакции).
Условие статической определимости фермы m + 3 = 2n
или m = 2n — 3 ( 2 )
Сравнивая ( 2 ) с ( 1 ), видим, что условие статической определимости совпадает с условием жесткости. Следовательно, жёсткая ферма без лишних стержней является статически определимой.
ОПРЕДЕЛЕНИE ОПОРНЫХ РЕАКЦИЙ
Для определения опорных реакций рассматриваем равновесие всей фермы в целом под действием произвольной плоской системы сил. Составляем три уравнения равновесия. После нахождения опорных реакций необходимо сделать проверку.
ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ФЕРМЫ Усилия в стернях фермы можно определить двумя способами: методом
вырезания узлов и методом сечения (метод Риттера).
Метод вырезания узлов состоит в следующем:
последовательно рассматривается равновесие всех узлов фермы, находящихся под действием внешних сил и реакций перерезанных стержней. К каждому узлу приложена плоская система сходящихся сил, для которой можно составить два уравнения равновесия. Расчёт целесообразно начинать с того узла, где сходятся два стержня. При этом одно уравнение равновесия предпоследнего узла и два уравнения последнего узла являются проверочными.
Метод Риттера состоит в следующем:
ферма, к которой приложены внешние силы, включая реакции опор, рассекается на две части по трём стержням, если это возможно. В число перерезанных стержней должны входить те усилия, которые требуется определить.
Одна из частей фермы отбрасывается. Действие отброшенной части на оставшуюся заменяется неизвестными реакциями.
Рассматривается равновесие оставшейся части. Уравнения равновесия составляются так, чтобы в каждое из них входило только одно неизвестное. Это достигается специальным выбором уравнений: при составлении уравнения моментов моментная точка выбирается там, где пересекаются линии действия двух неизвестных усилий, которые в данный момент не определяются. При составлении уравнения проекций ось проекций выбирается перпендикулярно
5
двум параллельным усилиям.
При составлении уравнений равновесия обоими методами предполагается, что все стержни растянуты. Если результат получается со знаком минус, стержень сжат.
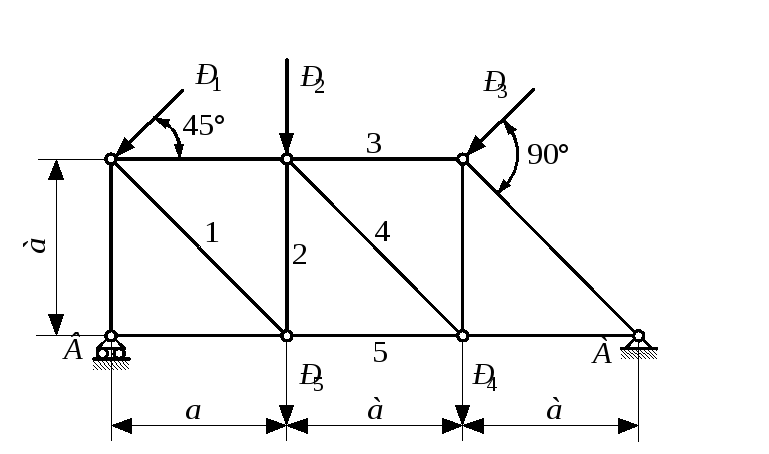
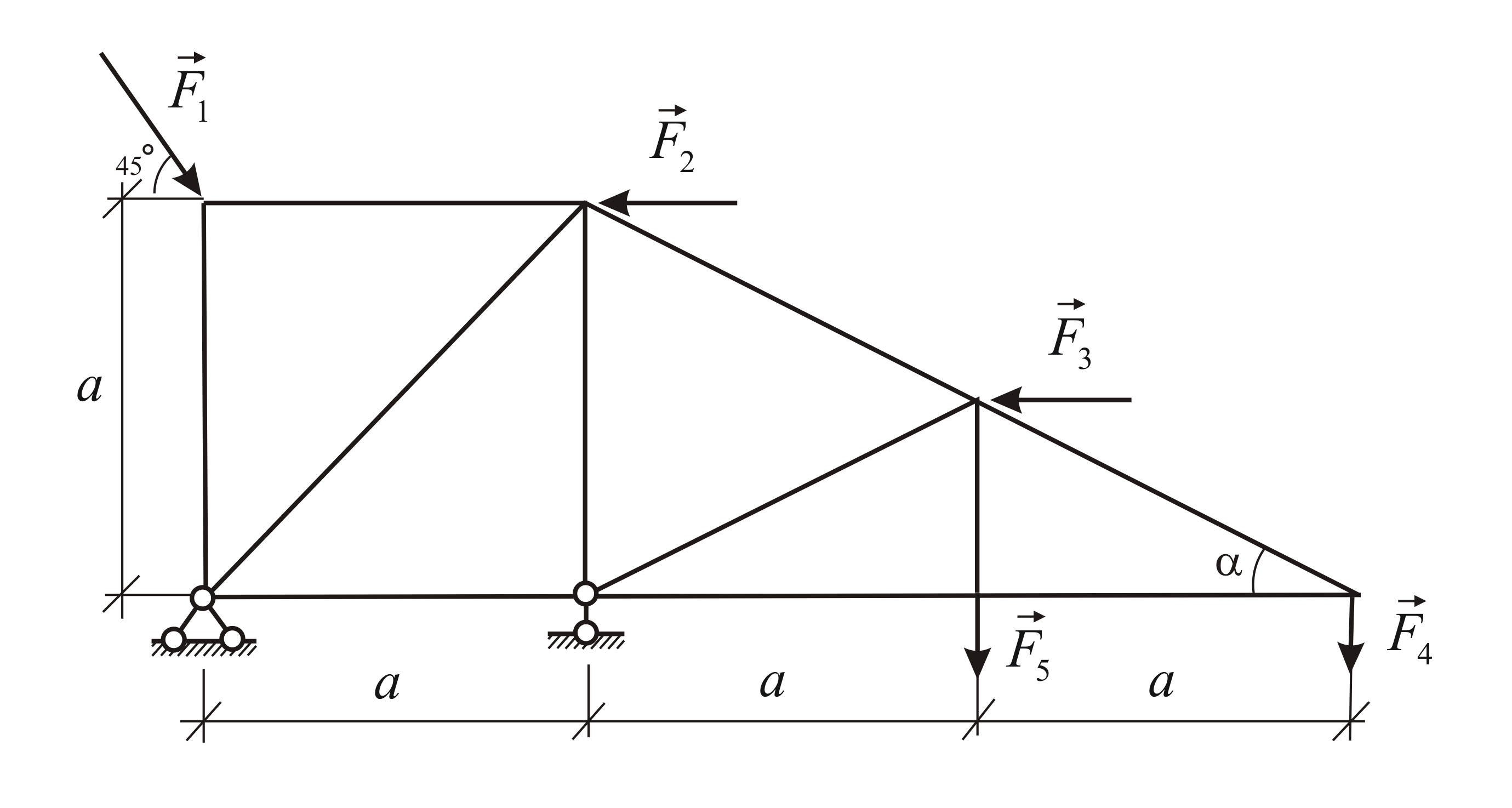
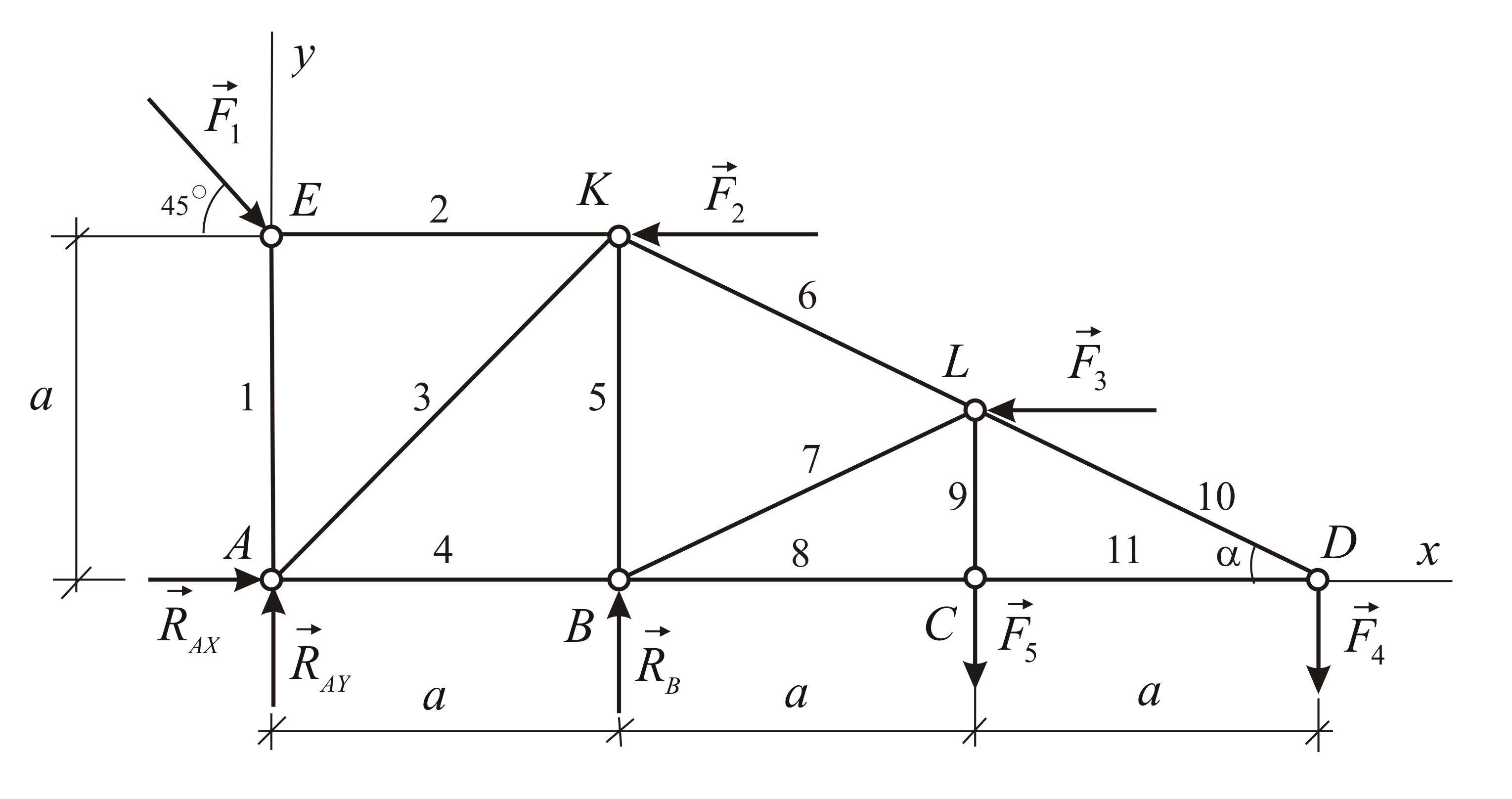
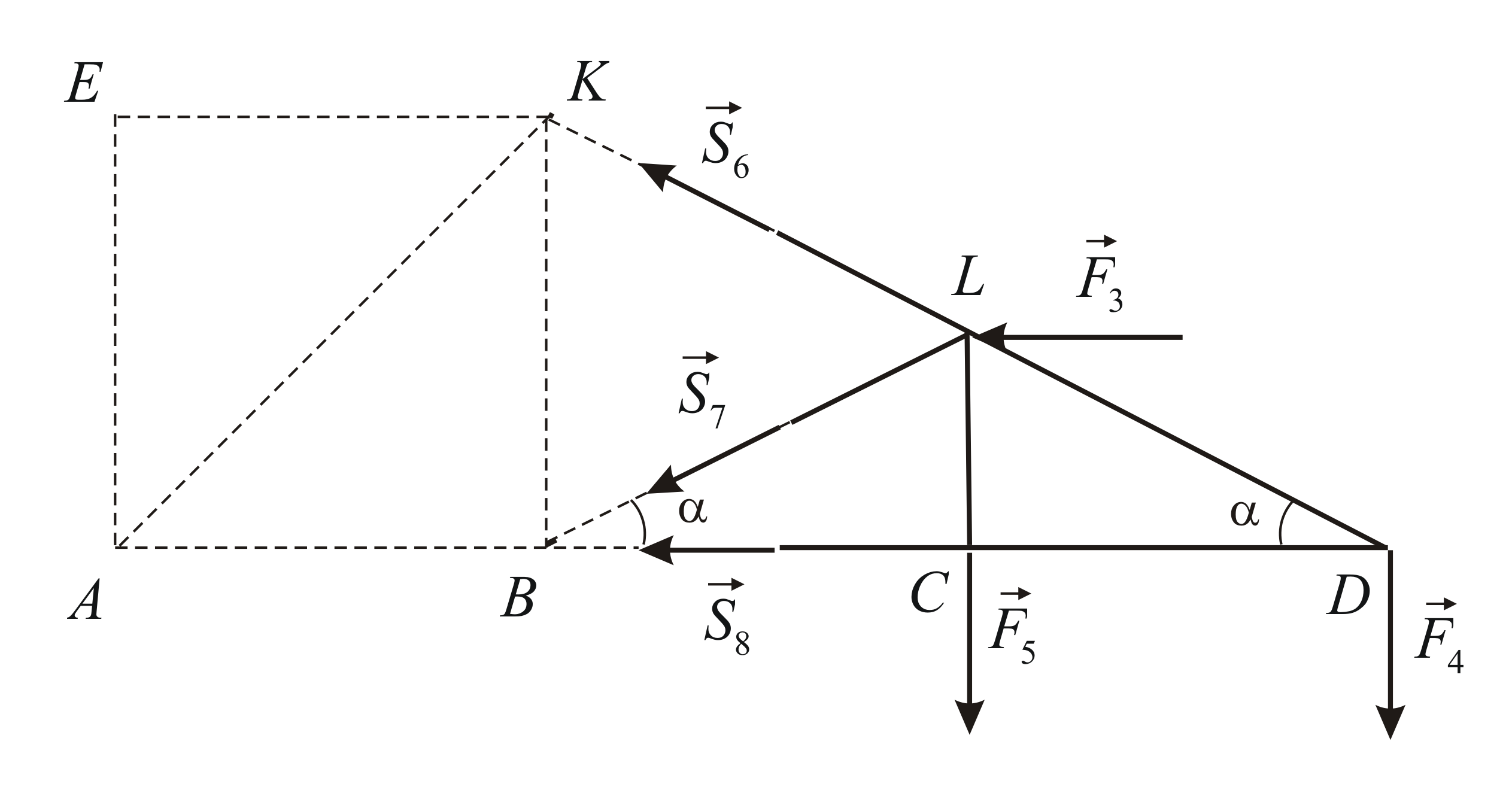
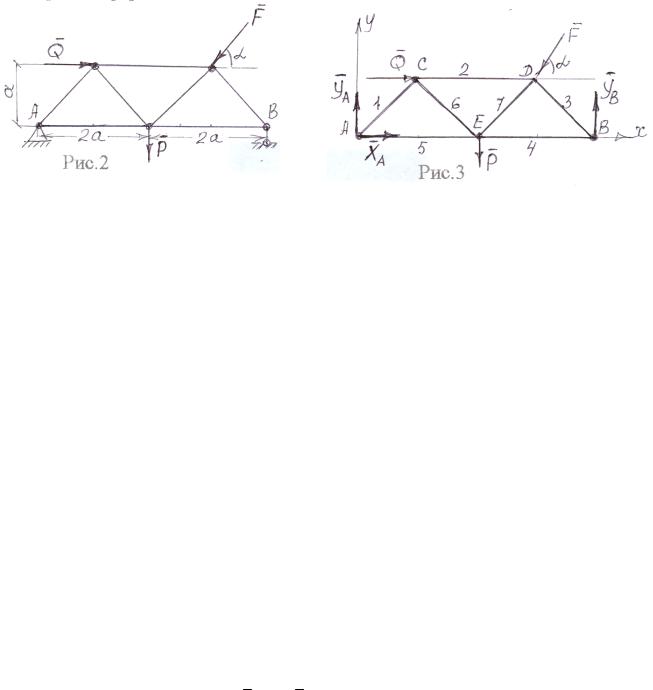
Типовой пример: Определить опорные реакции и усилия в стержнях фермы, если F=20 kH, P=20 kH, α=60°, Q=30 kH.( рис. 2, 3 ).
Определяем опорные реакции, рассматривая равновесие системы в целом ( рис.3 ).
∑X = 0:ХА –F · соs α + Q = 0;
∑Н = 0:YА + YВ – Р – F · sin α = 0;
∑MА = 0:-Q · а – Р · 2а – F · sin α · 3а + F · соs α · а + YВ · 4а = 0.
Решая эти уравнения, находим:
ХА = -20 kH; YА = 9.33 kH; YВ = 28 kH.
Проверим правильность полученных результатов. Для этого составим сумму моментов сил относительно точки С.
∑ МС = ХА · а – YA · а – Р · а – F · sin α · 2а + YВ · 3а = = (-20 – 9.33 – 20 — 20·1.73 + 28 · 3) ·а = 0.
Переходим к определению усилий в стержнях фермы.
Метод вырезания узлов.
Начинаем расчёт с узла А, где сходятся два стержня.
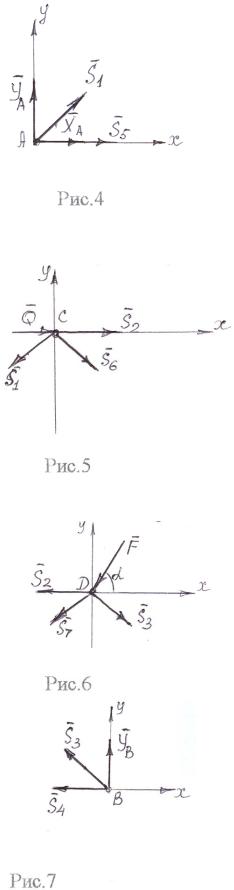
Следует изобразить тот узел, равновесие которого рассматривается (рис.4). Так как мы предполагаем, что все стержни растянуты, реакции стержней направляем от узла ( S1 и S5 ). Тогда усилия в стержнях (реакции
|
|
| 6 |
шарнира) | будут | направлены | в противоположную сторону. |
Для узла А составляем два уравнения равновесия:
∑Х = 0:+ХА + S5 + S1 · cos 45° = 0;
∑Y = 0:YА + S1 · cos 45° = 0.
Получаем: S1 13.2kH;
S5 29.32kH.
Далее рассматриваем равновесие узла С (рис.5). Уравнения равновесия:
∑Х = 0:Q + S2 + S6 · cos 45° — S1 · cos 45°= 0;
∑Y = 0:- S1 · cos 45° — S6 · cos 45° = 0.
При подстановке значения S1 учитываем, что усилие отрицательное.
Получаем: S6 13.2kH;
S2 48.7kH.
Аналогично рассчитываются остальные узлы (рис. 6,7).
∑Х = 0:- S2 – S7 · cos 45° — S3 · cos 45° — F · cos α= 0;
∑Y = 0:- S7 · cos 45° — S3 · cos 45° — F · sin α = 0.
Отсюда: S3 39.6kH;
S7 15.13kH.
∑Х = 0:- S4 – S3 · cos 45° = 0;
Второе уравнение проверочное:
∑Y = +YB + S3 · cos 45° = 28-39.6 · 0.71 =0. S4 = 28.0kH.

7
Для проверки рассмотрим равновесие узла Е.(Рис.8 )
∑Х = — S5 + S4 – S6 · cos 45° + S7 · cos 45° = 0;
∑Y = S6 · cos 45° + S7 · cos 45° — P = 0.
Так как уравнения обратились в тождества, то расчёт сделан верно.
Метод сечения (метод Риттера).
Метод Риттера удобно использовать, если требуется определить усилия не во всех стержнях, и как проверочный, так как он позволяет определить каждое усилие независимо от остальных.
Определим усилия в стержнях 2, 6, 5. Разрезаем ферму на две части по стержням 2, 6, 5. Отбрасываем правую часть и рассматриваем равновесие левой
(рис. 9 )..
Для определения усилия S5 составляем уравнение моментов относительно точки, где пересекаются силы S2 и S6 (точка С).
∑ МС = 0: ХА · а – YA · а + S5 · a = 0;. S5 = 29.32 kH.
Для определения усилия S2 составляем уравнение моментов относительно точки Е:
∑ МЕ = 0:- Q · а – S2 · а – YA · 2а =0; S2 = 48.64kH.
Для определения усилия S6 следует составить уравнение проекций на ось Y:
∑ Y = 0:-S6 · cos 45° + YA = 0; S6 = 13.2kH.
Результаты следует занести в табл. 1.

8
Усилия в стержнях фермы, кН
№ стержня, способ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
Способ | вырезания | -13,2 | -48,7 | 39,6 | 28,0 | 29,32 | 13,2 | 15,3 |
узлов |
|
|
|
|
|
|
|
|
Способ Риттера |
| -48,64 |
|
| 29,32 | 13,2 |
| |
РАСЧЁТ ФЕРМЫ С ПОМОЩЬЮ ПРИНЦИПА ВОЗМОЖННЫХ ПЕРЕМЕЩЕНИЙ
Принцип возможных перемещений является основным принципом аналитической механики. Он даёт самые общие методы решения задач статики и позволяет определять каждое неизвестное усилие независимо от всех остальных, составляя для него одно уравнение равновесия.
Принцип возможных перемещений (теорема ЛагранжаОстроградского):
Для равновесия механической системы, подчиненной идеальным, геометрическим и стационарным связям, необходимо и достаточно, чтобы сумма работ активных сил, действующих на систему, была равна нулю на любом возможном перемещении системы:
n
Аk(а) 0 . k 1
Стационарные связи — связи, явно не зависящие от времени.
Идеальные связи — связи, сумма работ реакций которых на любом возможном перемещении системы равна нулю.
Геометрические связи — связи, накладывающие ограничения только на координаты точек системы.
Активные силы — силы, действующие на систему, кроме реакций связи.
Возможные перемещения системы
Возможные перемещения механической системы — бесконечно малые перемещения системы, допускаемые наложенными на неё связями.
Величины возможных перемещений обозначаются символами, например — δ S, δφ, δХ.
Приведём примеры возможных перемещений систем (ограничимся рассмотрением плоских систем):
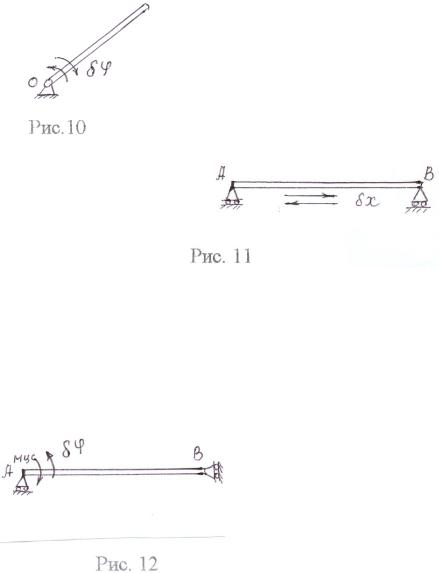
1. Тело закреплено неподвижным шарниром, позволяющим телу вращаться вокруг оси, проходящей через точку О, перпендикулярно
9
плоскости чертежа (рис. 10).
Возможное перемещение тела — поворот вокруг оси на угол δφ.
2. Тело закреплено двумя подвижными шарнирами
(рис.11).
Эти связи позволяют телу перемещаться поступательно параллельно плоскостям катков.
Возможное перемещение тела — δХ.
3.Тело тоже закреплено двумя подвижными шарнирами (плоскости катков не параллельны).
Эти связи позволяют плоскому телу перемещаться только в плоскости чертежа. Возможное перемещение этого тела будет плоскопараллельным перемещением. А плоскопараллельное перемещение тела можно в данный момент рассматривать как вращательное движение вокруг оси, проходящей через
мгновенный центр скоростей тела (м.ц.с. ) перпендикулярно плоскости чертежа
( рис. 12 )..
Следовательно, чтобы увидеть возможное перемещение данного тела, надо знать, где находится м.ц.с. этого тела. Чтобы построить м.ц.с., нужно знать направления скоростей двух точек тела, провести перпендикуляры к скоростям в этих точках, точка пересечения перпендикуляров и будет м.ц.с. тела. В примере нам известны направления скоростей точек А и В (они параллельны плоскостям катков ). Значит, возможное перемещение этого тела — поворот на угол δφ вокруг оси, проходящей через точку А перпендикулярно плоскости чертежа.
ВЫВОД: Так как в дальнейшем рассматриваются только плоские системы, то чтобы увидеть возможное перемещение системы, состоящей из плоских твёрдых тел, надо для каждого твёрдого тела увидеть или построить

|
| 10 |
м.ц.с. | Тогда | возможным перемещением каждого твёрдого тела |
будет поворот вокруг своего м.ц.с., или тело будет двигаться поступательно, если м.ц.с. отсутствует. Возможные перемещения системы определяются только связями, наложенными на систему, и не зависят от сил, действующих на систему. В случае геометрических и стационарных связей направления возможных перемещений точек системы совпадают с направлениями скоростей этих точек при реальном движении.
Работа силы на возможном перемещении
В рассматриваемых задачах твёрдые тела будут иметь возможность либо двигаться поступательно, либо вращаться вокруг оси, перпендикулярной плоскости чертежа. 3апишем формулы для нахождения возможной работы силы при таких перемещениях тел.
1.Тело движется поступательно.
Тогда каждая точка тела перемещается на r . Следовательно, точка приложения силы F перемещается на r . Тогда A F r .
Частные случаи:
A F r
A F r
A 0.
2.Тело вращается вокруг оси.
Работа силы F находится как элементарная работа силы, приложенной к вращающемуся телу. Тело поворачивается на угол δφ.
Тогда
δА = Мz ( F ) · δφ,
где Мz ( F ) — момент силы F относительно оси вращения тела (в наших задачах ось z перпендикулярна плоскости чертежа и нахождение Мz( F ) сводится к нахождению момента силы F относительно точки пересечения оси с плоскостью ).
δА > 0, если сила создаёт момент, направленный в сторону вращения тела;.
δА < 0 , если сила создаёт момент, направленный в сторону, противоположную вращению тела.
Плоские фермы. Способы расчета — Студопедия.Нет
Фермой называется стержневая система, остающаяся геометрически неизменяемой после условной замены ее жестких узлов шарнирными.
Плоские фермы могут воспринимать нагрузку, приложенную только в их плоскости, и закрепляются опорными связями, лежащими в этой же плоскости. Пространственные фермы способны воспринимать нагрузку, действующую в любом направлении. Примером фермы может служить башенная конструкция (кран, опоры высоковольтных передач и т. п.).
Если ферма в целом под действием сил, приложенных к ее узлам, находится в равновесии, то и любой из ее узлов также будет находиться в равновесии, т. е. внешняя нагрузка, действующая на узел, и внутренние усилия в стержнях, сходящихся в данном узле, взаимно уравновешиваются.
Простейшая плоская ферма – треугольная, состоящая из трёх стержней и трёх узлов.
Рассмотрим принципы вычисления внутренних усилий в стержнях плоской фермы. При действии на ферму сосредоточенных сил, приложенных в узлах (шарнирах), в ее прямолинейных стержнях возникают продольные (растягивающие или сжимающие) силы.
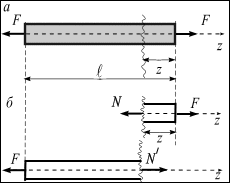 |
| Рис. 3.24 |
Растяжением или сжатием стержней называется такой вид деформации, при которой все внешние нагрузки или их равнодействующие действуют вдоль оси стержня (осевые нагрузки) (рис. 3.24, а).
Для их вычисления используется метод сечения. Мысленно рассечем стержень плоскостью, перпендикулярной к его оси, проведём произвольное сечение z (рис. 3.24, б), и приложим к сечению неизвестную силу  , направленную по внешней нормали к сечению.
, направленную по внешней нормали к сечению.
Равновесие отсеченной части возможно тогда, когда силы, действующие на отсеченную часть, равны друг другу по модулю и направлены в противоположные стороны. Запишем аналитическое условие равновесия для сечения z:
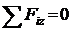 ,
, 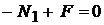 ,
,  .
.
Следовательно, при растянутом состоянии стержней усилия в отсеченном стержне направлены от узла вдоль стержня – это состояние обычно принимается за положительное. На рис. 3.25 показаны направления усилий 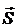 и
и 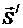 в стержне АВ, растянутом силами
в стержне АВ, растянутом силами 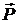 и
и 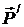 .
.
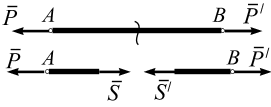
Рис. 3.25
При сжатом состоянии стержней усилия направлены от центра стержня к узлам.
При расчете фермы определяют реакции внешних наложенных связей и внутренние усилия в стержнях фермы.
Для расчета внутренних усилий в стержнях используют два способа: способ вырезания узлов и способ Риттера (или способ моментных точек).
Способ вырезания узлов. Мысленно вырезают узел фермы: указывают заданные силы, приложенные к этому узлу; действие отброшенной фермы заменяют усилиями в стержнях, присоединенных к этому узлу. Усилия направляют от узла к центрам стержней, т.е. считают их растянутыми, если при расчете получают знак минус – это означает, что стержень сжат. При вырезании узла получают систему сходящихся сил. Для плоской системы сходящихся сил система уравнений равновесия состоит из двух уравнений:
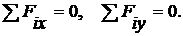
В связи с этим последовательность вырезания узлов в плоской ферме определяется числом неизвестных усилий, приложенных к этому узлу, – их должно быть не больше двух.
Способ Риттера (или способ моментных точек). Ферму мысленно делят сечением на две части и рассматривают равновесие одной из частей: указывают заданные силы, приложенные к этой части; действие отброшенной части фермы заменяют усилиями в стержнях, через которые провели сечение. Усилия направляют от узла к центрам стержней (в сторону к отброшенной части), т. е. считают их растянутыми. Таким способом получаем произвольную плоскую систему сил, равновесие которой определяется системой из трех уравнений, соответственно, сечение следует проводить не более чем через три неизвестных стержня. При составлении уравнений используют уравнения моментов относительно точек, где пересекаются линии действия неизвестных усилий – эти точки называют моментными точками, или точками Риттера.
Содержание контрольных работ для студентов на тему «расчет плоских ферм» дано в приложении (контрольная работа 3, задача 2).
Пример 3.6. Рассмотрим плоскую ферму, показанную на рис. 3.26.
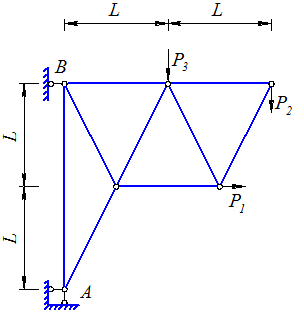
Рис. 3.26
Дано: P1 = 10 кН; P2 = 21 кН; P3 = 15 кН; L = 2 м.
Требуется:
· вычислить реакции опор от заданной нагрузки;
· проверить правильность полученных результатов;
· вычислить усилия в стержнях фермы способом вырезания узлов;
· проверить правильность полученных результатов методом сплошных сечений;
· проанализировать полученные результаты.
Решение:
Из геометрии задачи вычислим значение косинусов и синусов углов, образованных стержнями в узлах фермы (рис. 3.27):
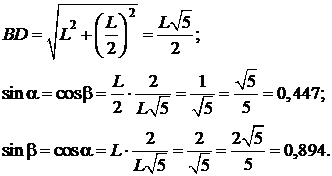
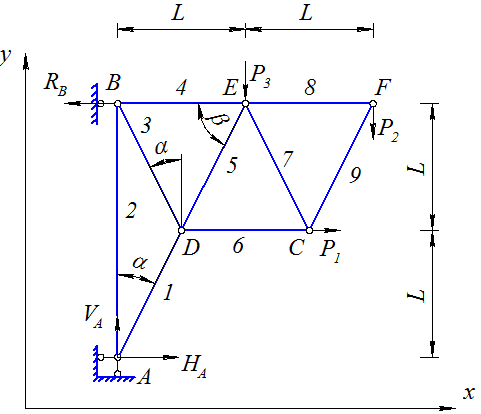
Рис. 3.27
Составим систему уравнений равновесия:

Решаем эту систему:

Проверка:
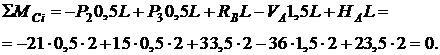
Получили: RB = 33,5 кН, НA=23,5кН, VA=36 кН.
Вычисление усилий в стержнях (способ вырезания узлов).
Последовательно вырезаем узлы и составляем условия равновесия для системы сходящихся сил: внешних сил и усилий в стержнях, приложенных к этому узлу.
При аналитическом способе решения считаем все стержни в растянутом состоянии (усилие направляем от узла к центру стержня).
При геометрическом способе показываем верное направление усилий.
Узел А (рис. 3.28)
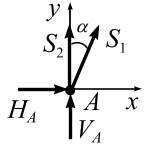 | 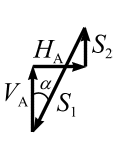 |
| а | б |
Рис. 3.28 | |
Система уравнений равновесия:
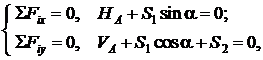
откуда

Сделаем графическую проверку, построив замкнутый силовой многоугольник (построение выполняется в масштабе рис. 3.28, б).
Узел В (рис. 3.29)
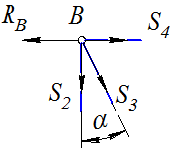 | 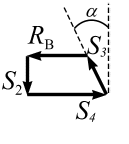 |
| а | б |
Рис. 3.29 | |
Система уравнений равновесия:
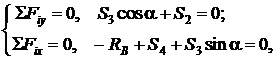
откуда
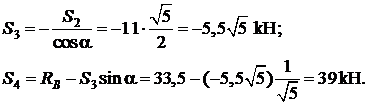
Сделаем графическую проверку, построив замкнутый силовой многоугольник (рис. 3.29, б)
.
Узел D (рис.3.30)
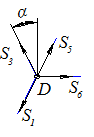 | 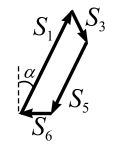 |
| а | б |
Рис. 3.30 | |
Система уравнений равновесия:

откуда
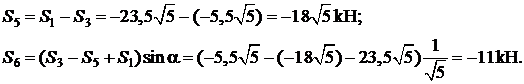
Сделаем графическую проверку, построив замкнутый силовой многоугольник (рис. 3.30, б).
Узел Е (рис. 3.31)
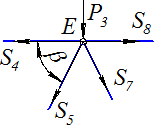 | 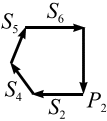 |
| а | б |
Рис. 3.31 | |
Система уравнений равновесия:
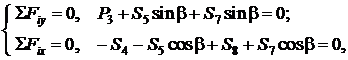
откуда
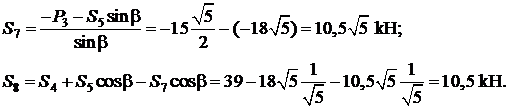
Сделаем графическую проверку, построив замкнутый силовой многоугольник (рис. 3.31, б).
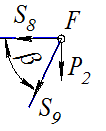
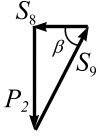
Узел F (рис. 3.32)
 |  |
| а | б |
Рис. 3.32 | |
Осталось вычислить S9. Для этого достаточно составить одно уравнение:
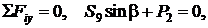
откуда
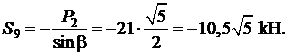
Сделаем графическую проверку, построив замкнутый силовой многоугольник (рис. 3.32, б).
Способ Риттера.Проверим правильность расчета усилий в стержнях 4, 5 и 6. Для этого рассекаем ферму сечением, проходящим через эти три стержня, на две части и рассмотрим равновесие правой части фермы
(рис. 3. 33).
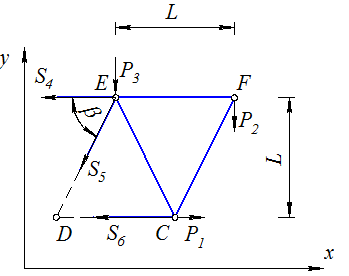
Рис. 3.33
Составим систему уравнений равновесия для произвольной плоской системы сил (уравнения моментов составляем относительно точек Риттера – D и E):

здесь ось y не перпендикулярна прямой (DE).
Отсюда
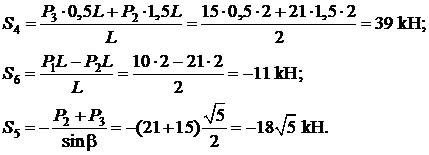
Значения усилий в стержнях, рассчитанные разными способами, совпадают.
Ответ: в (кН)
Вывод: стержни 2, 4, 7, 8 растянуты;
стержни 1, 3, 5, 6, 9 сжаты.
Расчет простых плоских ферм способом сечений
В качестве отдельного тела, составляющего ферму, может быть принята часть конструкции, включающая два узла и более. В этом случае внутренние силы, действующие между частями системы тел, уже не будут сходиться в одной точке. Для такой системы сил можно составить три независимых уравнения равновесия, из которых будут определены три неизвестные силы.
Причем, для получения уравнения с одной неизвестной силой составляют суммы моментов относительно точек пересечения линий действия двух других неизвестных реакций стержней. Если линии действия каких-либо двух сил параллельны, то составляется сумма проекций сил на ось, перпендикулярную указанным линиям действия.
Достоинство метода: можно определить силу реакции конкретного стержня, не рассчитывая другие внутренние силы.
Графический метод определения внутренних сил в стержнях простой плоской фермы (метод Максвелла-Кремоны)
Выше представлены аналитические способы расчета реакций стержней фермы. Однако при расчете ферм с большим количеством стержней их применение требует значительно больших затрат, чем использование графического метода, заключающегося в построении диаграммы Максвелла-Кремоны. Этот способ является графическим вариантом рассмотренного ранее способа вырезания узлов и состоит в построении замкнутых силовых многоугольников для каждого узла фермы. Его особенностью является метод обозначения сил. Он состоит в следующем. Место, занимаемое фермой, разбивается стержнями фермы и приложенными к ней внешними силами на области (зоны). Каждая сила тогда находится на границе зон и обозначается буквами, соответствующими названиям пограничных областей.
Построение диаграммы выполняется в следующем порядке.
Изображается в масштабе ферма, показываются все внешние силы (в том числе и определенные ранее реакции связей) с учетом их действительных направлений так, чтобы их векторы выходили за контур фермы.
Буквами обозначаются области, ограниченные линиями действия внешних сил и стержнями контура фермы.
Буквами обозначаются внутренние области, ограниченные стержнями фермы.
Строится силовой многоугольник внешних сил, приложенных к ферме. Записывается уравнение равновесия фермы в векторной форме: первое слагаемое соответствует одной из внешних сил, последующие получаются при обходе наружного контура фермы, например, по ходу часовой стрелки. В масштабе изображаются все векторы сил. Их начала и концы обозначаются буквами, соответствующими наименованиям зон. При правильном построении силовой многоугольник внешних сил должен быть замкнутым.
Выбирается узел, в котором имеется не более двух стержней, реакции которых неизвестны. Составляется уравнение его равновесия в векторной форме. Порядок следования векторов соответствует обходу узла в принятом ранее направлении. В соответствии с условием равновесия достраиваются недостающие стороны силового многоугольника.
Выполняются построения, описанные в пункте 5, до того момента, пока не будут определены все искомые силы. Полученная в результате построения фигура носит название диаграммы Максвелла-Кремоны.
Правильность ее построения проверяется по совпадению направлений линии действия последней определяемой внутренней силы и соответствующего стержня при рассмотрении предпоследнего узла.
7. Величины сил реакций стержней определяются путем измерения соответствующих отрезков на диаграмме и умножения на масштабный коэффициент.
Чтобы определить, сжат либо растянут рассматриваемый стержень, необходимо проверить, куда направлен соответствующий вектор силы. Если сила, действующая на узел, направлена от узла фермы – стержень растянут; иначе – сжат.
Задание С 10
Определение реакций опор и сил в стержнях плоской фермы
Определить реакции опор и усилия во всех стержнях фермы способом вырезания узлов. В стержнях 1, 2, 3, 4, 5 определить те же усилия способом Риттера. Схемы ферм изображены на рисунках, рис. С 10 – 1 – С 10 – 10 данные необходимые для расчетов указаны в табл. С 10.
Таблица С 10
Вариант | Р1 | Р2 | Р3 | Р4 | Р5 | а |
кН | м | |||||
1 | 4 | 2 | 0 | 5 | 1 | |
2 | 3 | 5 | 4 | 2 | 2 | |
0 | 1 | 4 | 2 | 5 | 1 | |
1 | 4 | 3 | 0 | 5 | 0,6 | |
3 | 0 | 2 | 1 | 2,5 | 0,5 | |
6 | 4 | 5 | 3 | 0 | 1 | |
5 | 2 | 0 | 4 | 6 | 2 | |
4 | 3 | 1 | 5 | 4 | 1 | |
2 | 1 | 3 | 0 | 5 | 0,5 | |
2 | 4 | 3 | 2,5 | 6 | 2 | |
3 | 4 | 1 | 4 | 2 | 1 | |
5 | 6 | 3 | 1 | 0 | 0,4 | |
Вариант | Р1 | Р2 | Р3 | Р4 | Р5 | а |
кН | м | |||||
3 | 4 | 1 | 2 | 5 | 2 | |
0 | 2,5 | 5 | 3 | 0 | 2,5 | |
6 | 5 | 2 | 4 | 1 | 1 | |
2 | 0 | 5 | 6 | 4 | 2 | |
5 | 4 | 1 | 5 | 3 | 0,5 | |
6 | 2 | 0 | 2,5 | 4 | 1 | |
6 | 3 | 4 | 5 | 1 | 0,6 | |
2 | 1 | 4 | 0 | 6 | 2 | |
1 | 2 | 6 | 4 | 3 | 1 | |
3 | 1 | 3 | 2,5 | 4 | 0,5 | |
1 | 2,5 | 3 | 5 | 0 | 2 | |
6 | 3 | 5 | 3,5 | 1 | 1 | |
3 | 6 | 2 | 4 | 2,5 | 0,6 | |
0 | 1 | 4 | 5 | 2 | 2 | |
4 | 1 | 3 | 5 | 2 | 0,6 | |
2,5 | 3 | 5 | 2 | 3,6 | 1 | |
4 | 0 | 1 | 6 | 2,5 | 2 | |
6 | 4 | 2 | 3,6 | 1 | 0,5 | |
2 | 4,5 | 0 | 1 | 5 | 1 | |
4 | 2 | 2,5 | 3 | 1 | 2 | |
4,2 | 5 | 3 | 0 | 6 | 0,5 | |
2 | 3 | 4 | 2,5 | 0 | 1 | |
1 |
|
Рис. С 10 – 1
Рис. С 10 – 2
Рис. С 10 – 3
Рис. С 10 – 4
Рис. С 10 – 5
Рис. С 10 – 6
Рис. С 10 – 7
Рис. С 10 – 8
Рис. С 10 – 9
33 |
|
34 |
|
Рис. С 10 – 10
2.2. Расчёт ферм
Особое место в ряду статических задач занимает расчёт ферм. Фермой называется жёсткая конструкция из прямолинейных стержней. Если все стержни фермы и вся приложенная к ней нагрузка расположены в одной плоскости, ферма называется плоской. В дальнейшем будем рассматривать только плоские фермы. Соединения стержней называются узлами фермы.
В результате полного расчёта фермы необходимо определить реакции опор и усилия во всех стержнях фермы.
При расчёте ферм приложенную внешнюю нагрузку (включая весовую нагрузку) заменяют эквивалентной системой, силы которой приложены к узлам фермы. В реальных фермах соединения стержней, как правило, жёсткие (сварка, клёпка и т.д.), так что они не допускают относительного поворота стержней. В расчётной схеме крепления стержней считаются шарнирными, причём, трение в шарнирах считается пренебрежимо малым.
В результате сделанных упрощающих предположений оказывается, что каждый стержень находится в равновесии под действием двух сил, приложенных к его концам. Эти силы должны иметь общую линию действия, т.е. они направлены вдоль стержня. Таким образом, считается, что каждый стержень фермы работает или на растяжение, или на сжатие, но не может испытывать кручения или изгиба. Усилие в стержне считается положительным, если он растянут.
Для определения усилий в стержнях фермы используются два основных метода.
Пример
Рассчитать ферму, изображённую на Рис. 2.18.
Дано: 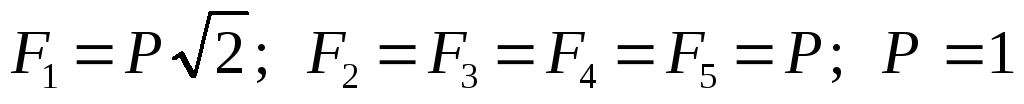 кН;
кН;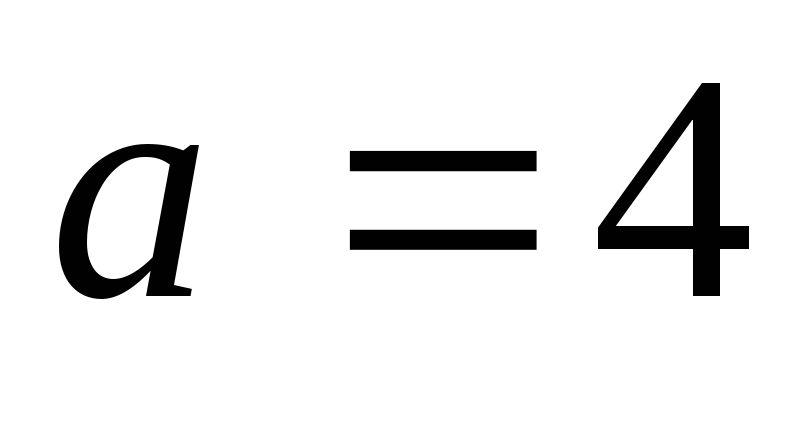 м.
м.
|
Рис. 2.18 |
Прежде всего обозначим все узлы и все стержни фермы. Определим реакции опор. Для этого рассмотрим равновесие фермы в целом (Рис. 2.19). Составим условия равновесия:
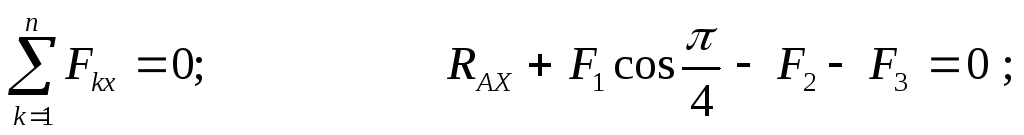
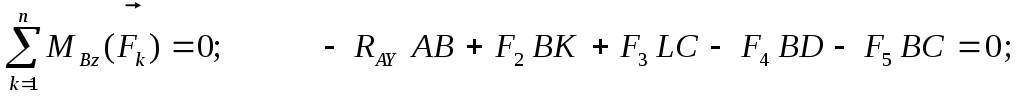

Отсюда:
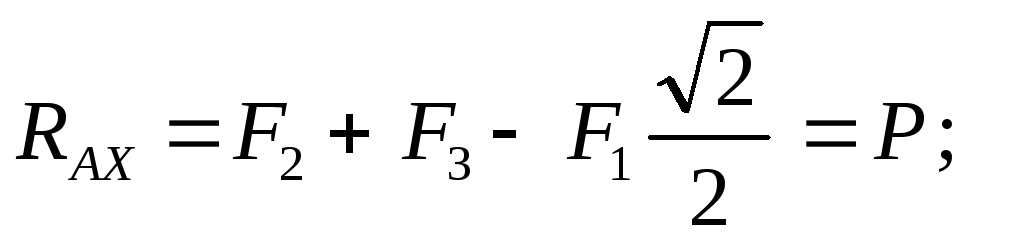
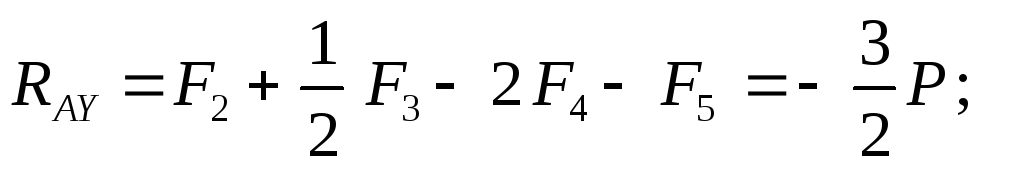
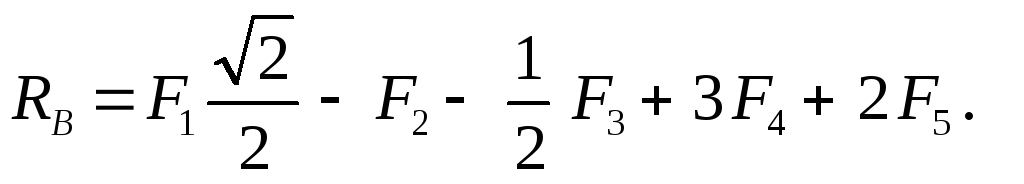
|
Рис. 2.19 |
Поскольку вычисленные величины
опорных реакций определяют весь
дальнейший расчёт, имеет смысл проверить
полученные результаты, составив,
например, уравнение моментов относительно
оси 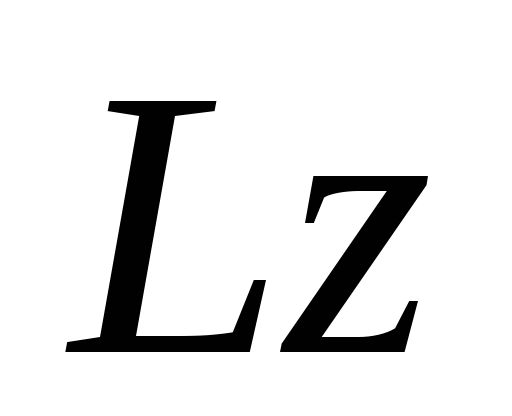 (чтобы в это уравнение вошли все
вычисленные величины):
(чтобы в это уравнение вошли все
вычисленные величины):
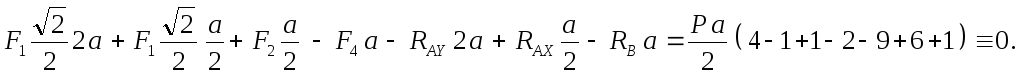
Для определения усилий в стержнях фермы используются два основных метода.
Метод вырезания узлов.Метод состоит в том, что рассматривается равновесие каждого узла фермы в определённой последовательности. На узел действует плоская система сходящихся сил, для которой можно составить два уравнения равновесия, что позволяет определить две неизвестные. Поэтому расчёт начинают с узла, соединяющего два стержня фермы. Затем переходят к соседним узлам в определённой последовательности, которая позволяет на каждом шаге определять усилия в очередных двух стержнях. Первоначально предполагается, что стержни растянуты, т.е. их реакции направлены от узлов. Если усилие в каком-либо стержне оказывается отрицательным, то это означает, что данный стержень сжат.
Заметим, что уравнения равновесия фермы в целом являются прямым следствием полной системы уравнений равновесия узлов, так что методом вырезания узлов можно определить в том числе и реакции опор фермы. Но в этом случае часто приходится совместно решать систему, содержащую значительное число уравнений. Предварительное определение реакций опор упрощает решение задачи, а неиспользованные уравнения равновесия узлов можно рассматривать как проверочные.
Рассмотрим
равновесие узла 

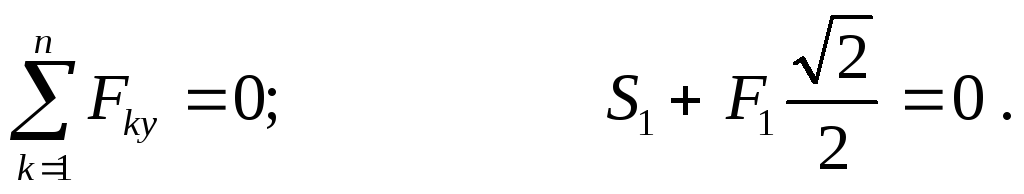
Отсюда: 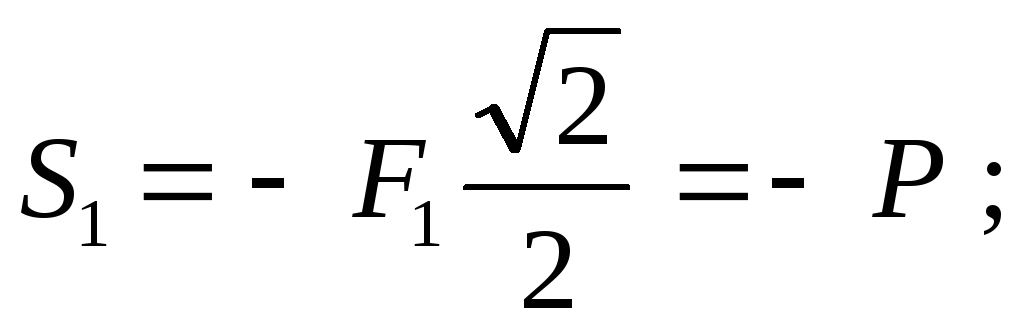 (стержень сжат)
(стержень сжат)
 (стержень сжат).
(стержень сжат).
Рассмотрим
равновесие узла 
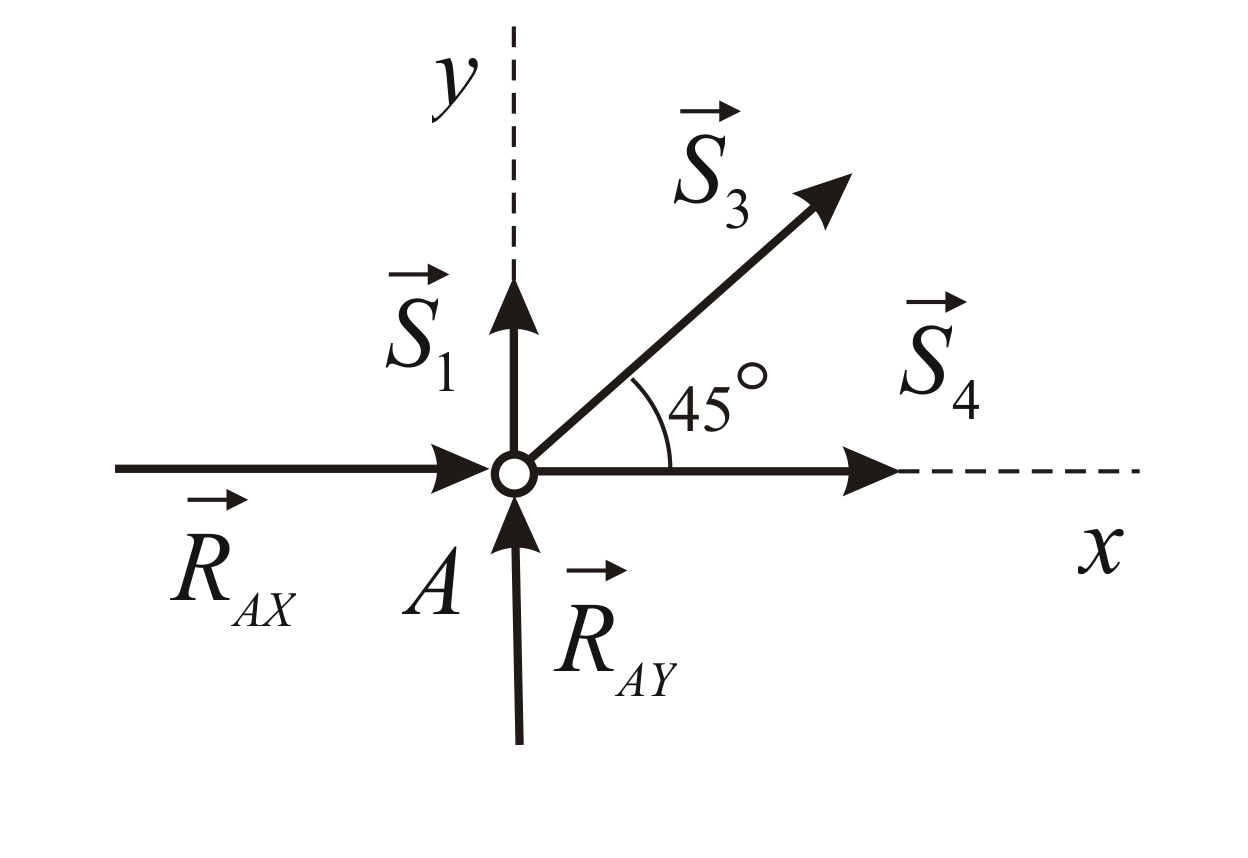
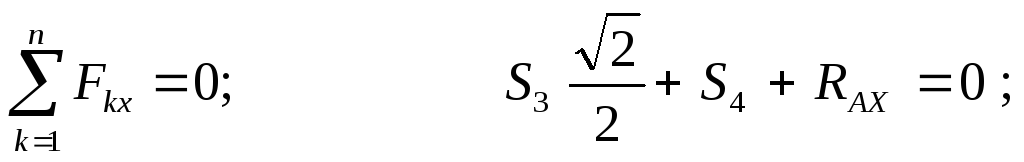
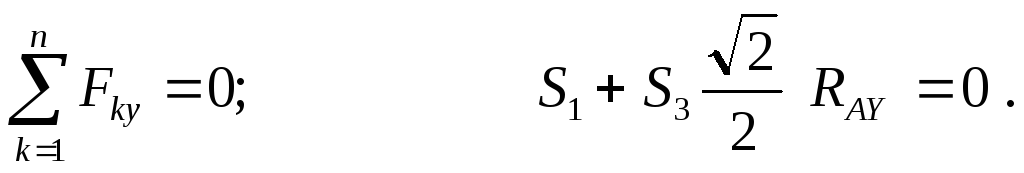
Отсюда:
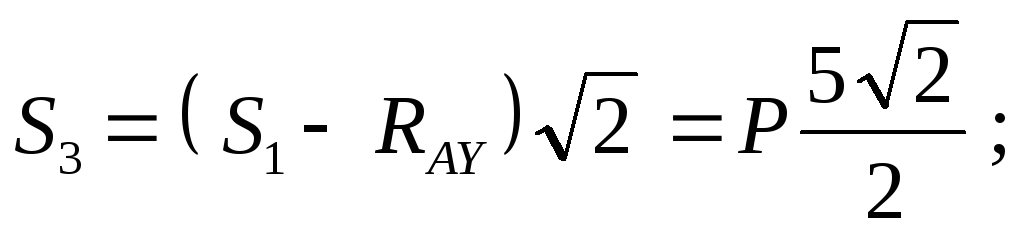 (стержень растянут)
(стержень растянут)
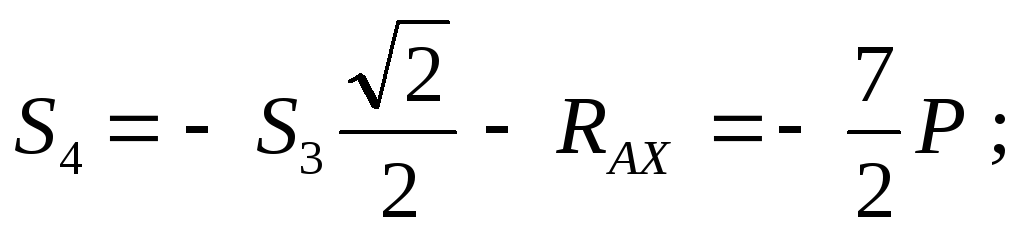 (стержень сжат).
(стержень сжат).
Рассмотрим
равновесие узла 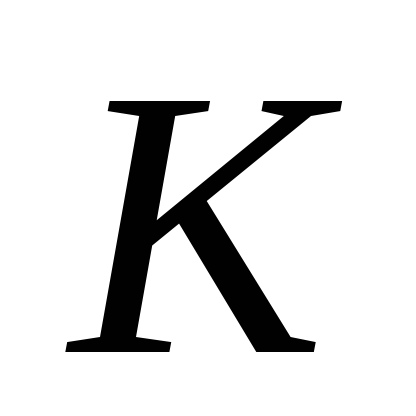
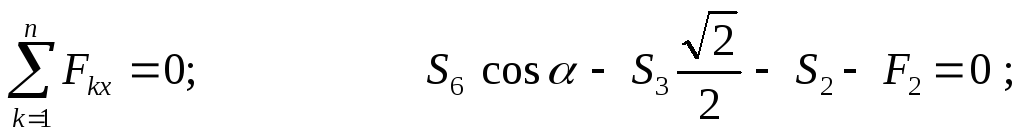
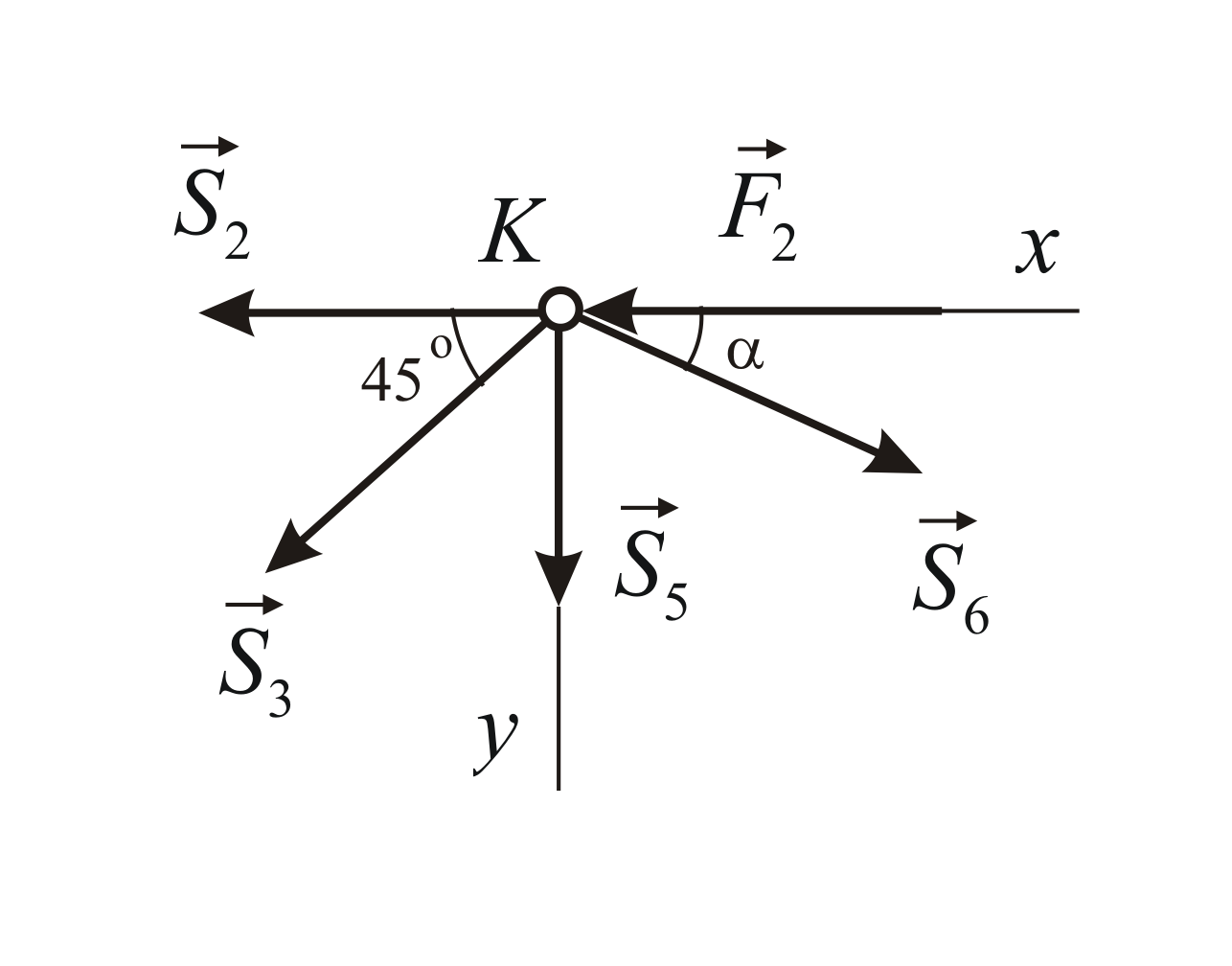

Значения
тригонометрических функций определим
из треугольника 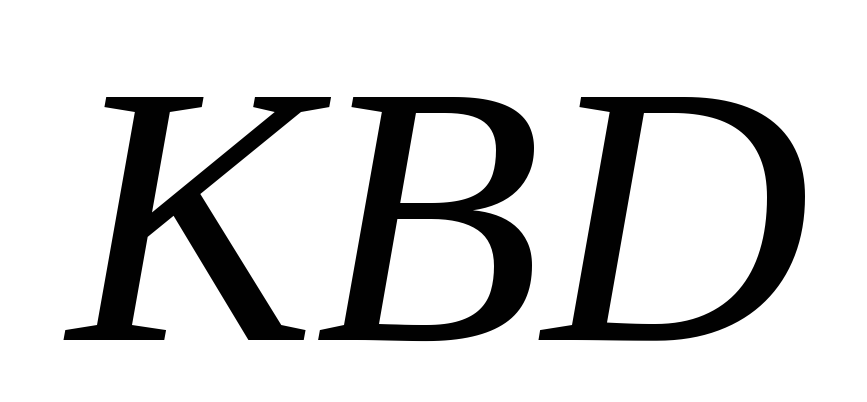 :
:
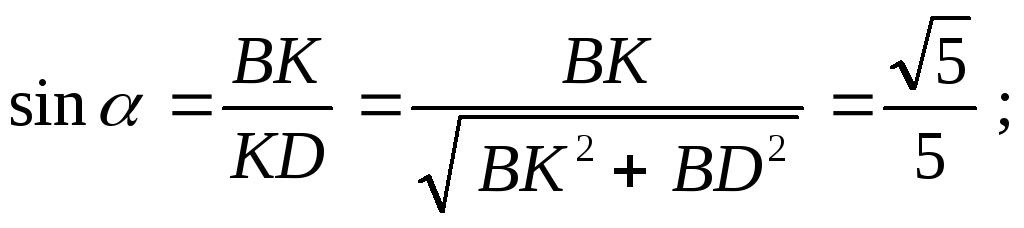
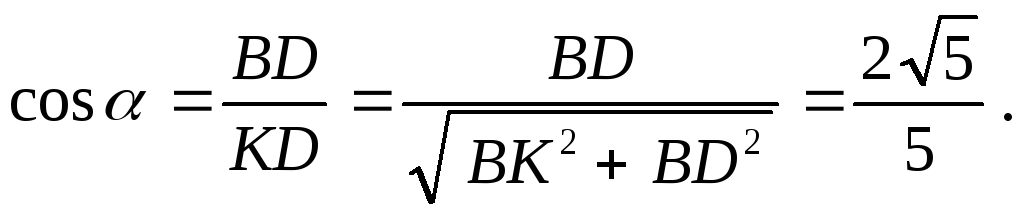
Таким образом,
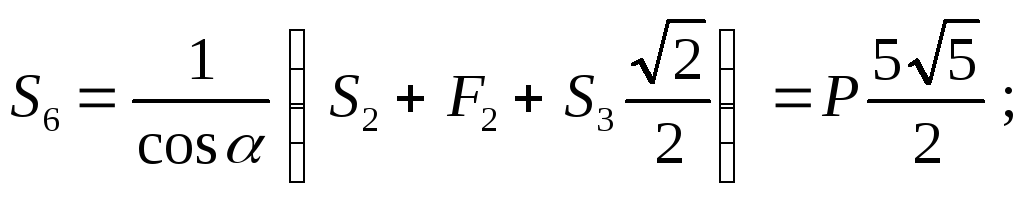 (стержень растянут)
(стержень растянут)
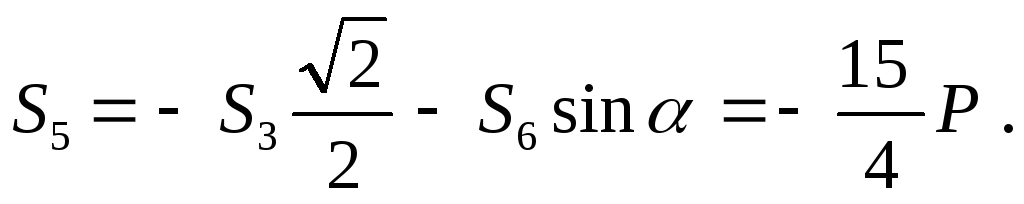 (стержень сжат).
(стержень сжат).
Рассмотрим
равновесие узла 
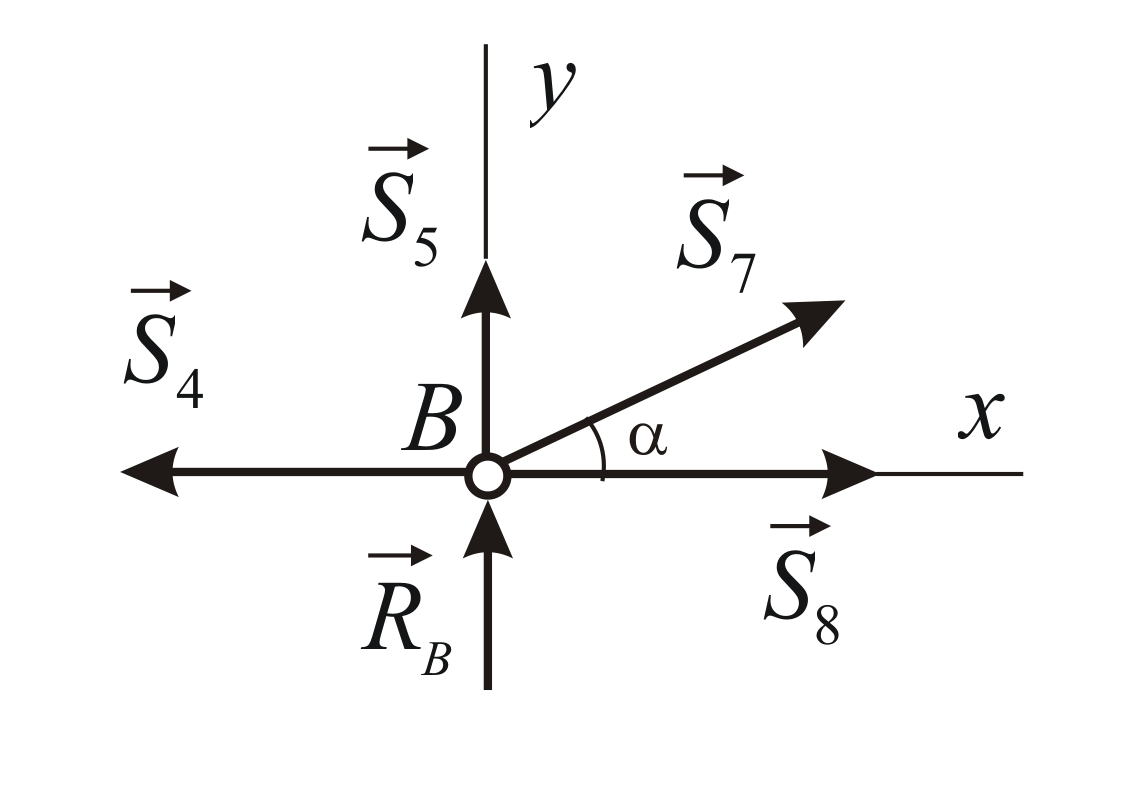
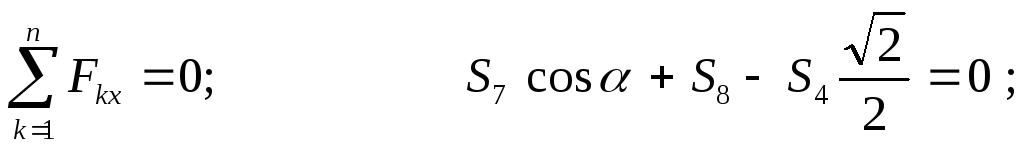
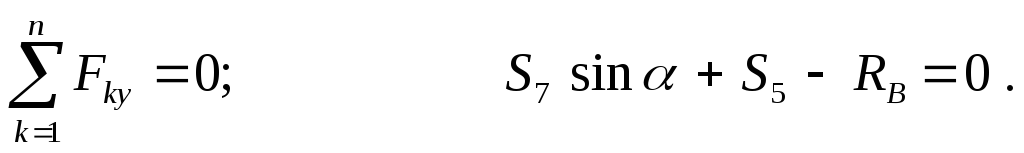
Отсюда:
(стержень сжат).
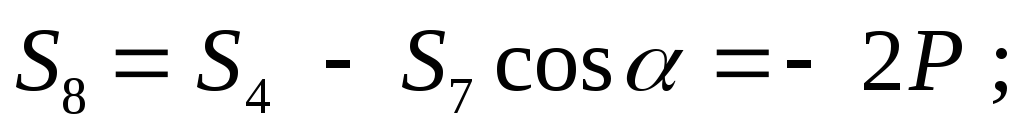 (стержень сжат).
(стержень сжат).
Р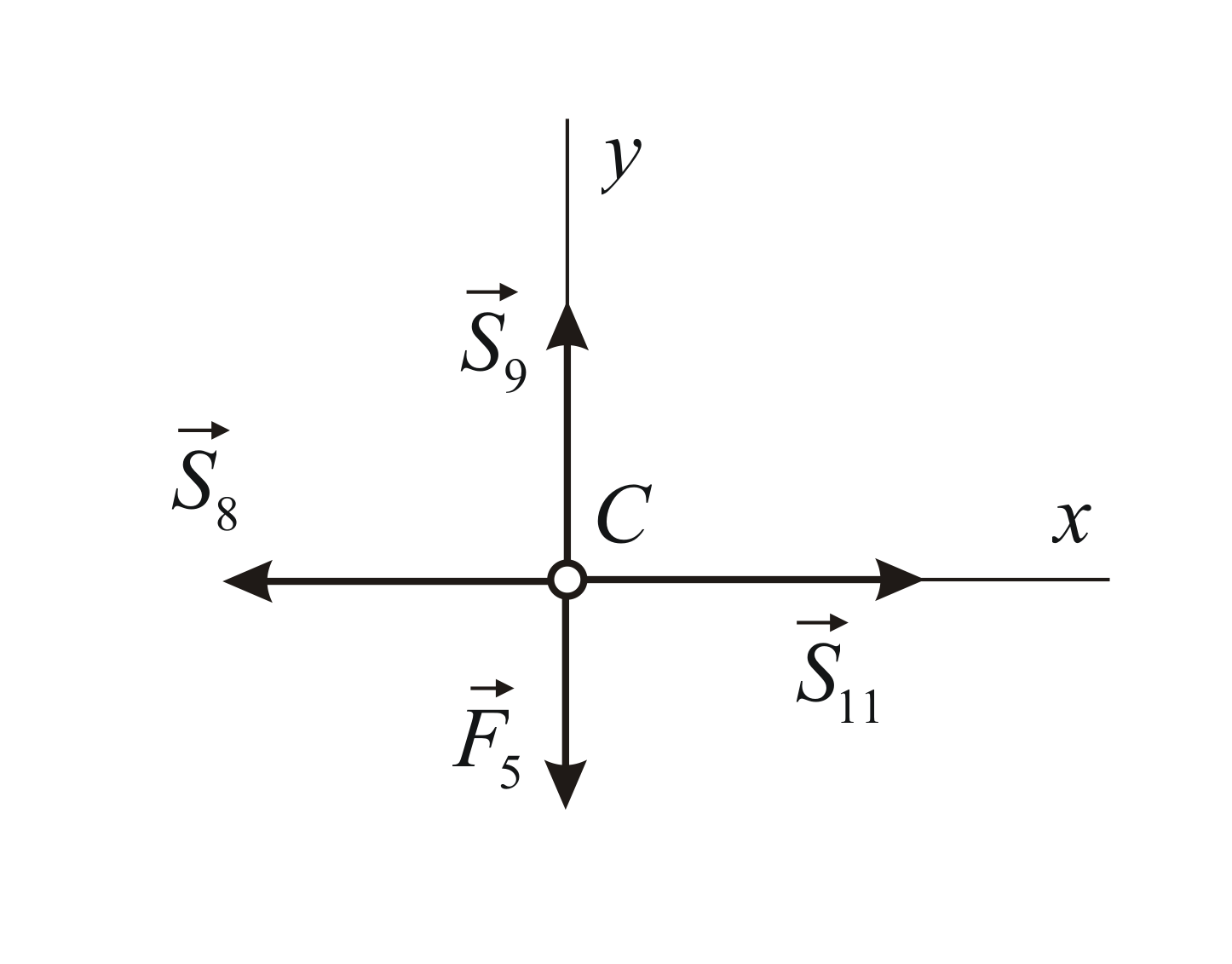 ассмотрим
равновесие узла
ассмотрим
равновесие узла
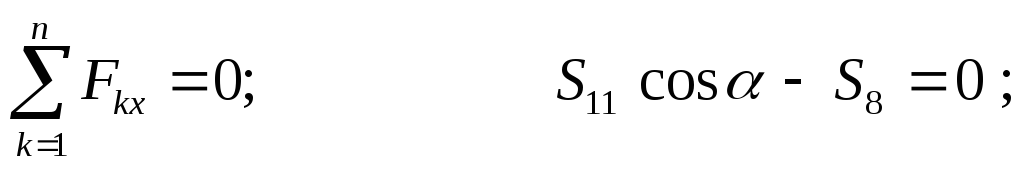

Отсюда:
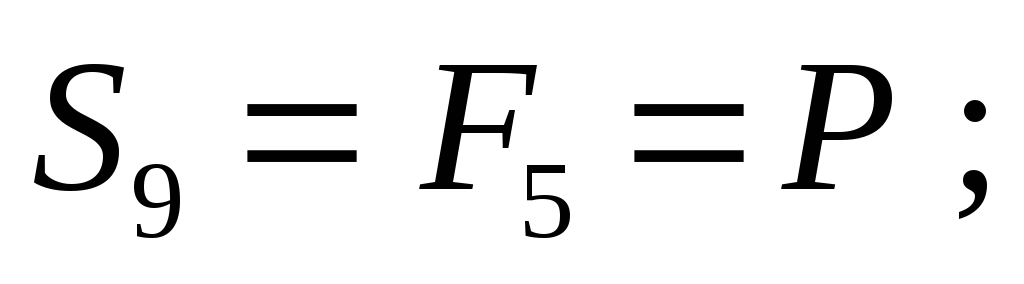 (стержень растянут)
(стержень растянут)
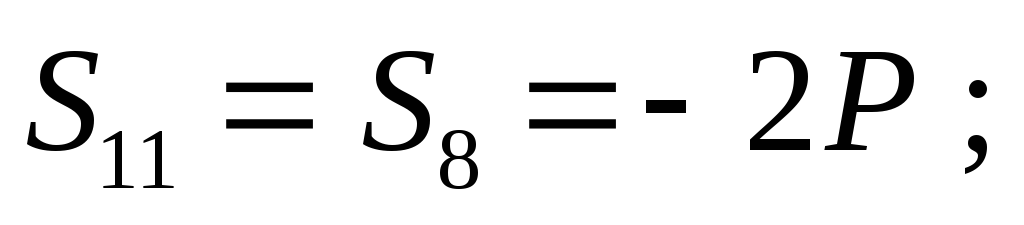 (стержень сжат).
(стержень сжат).
Рассмотрим
равновесие узла 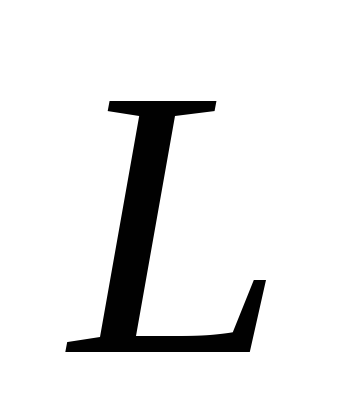
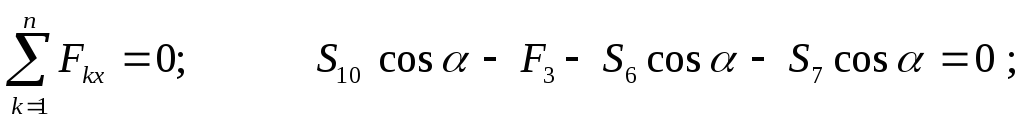
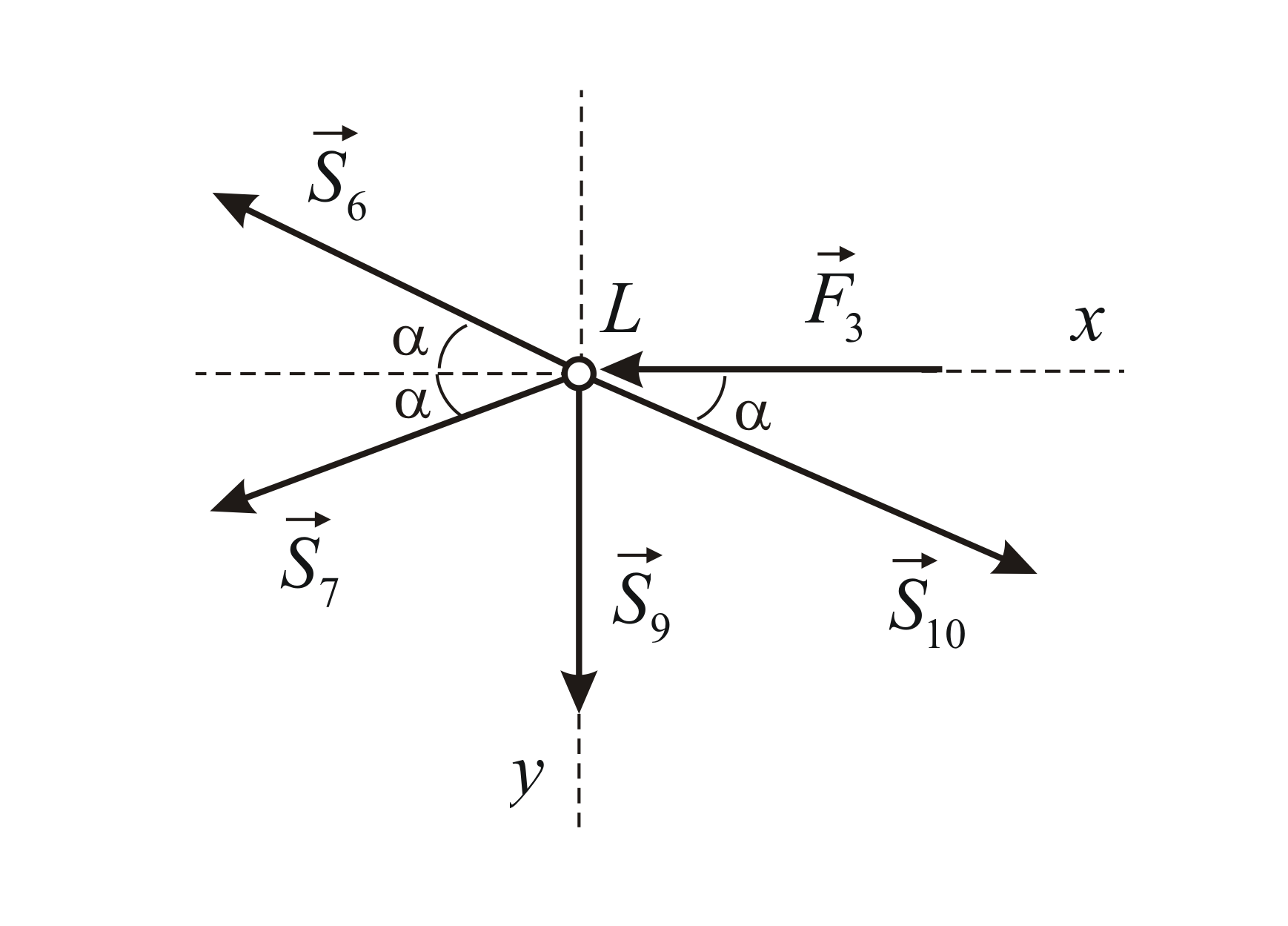
Отсюда:
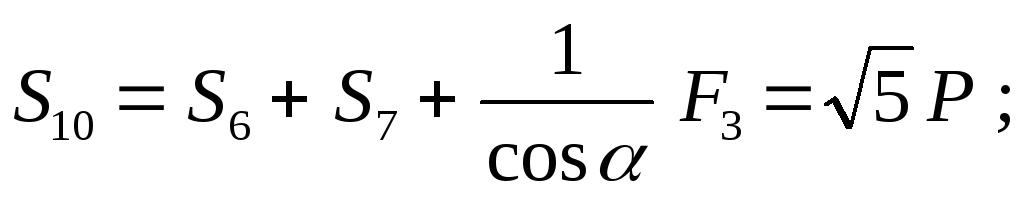 (стержень растянут)
(стержень растянут)
Таким образом, определены усилия во всех стержнях фермы. Оставшиеся уравнения используем для проверки полученных результатов.
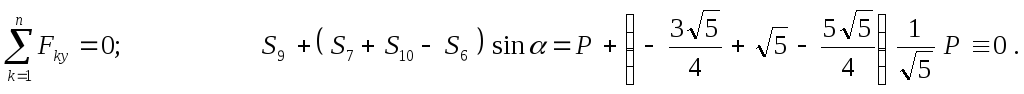
Р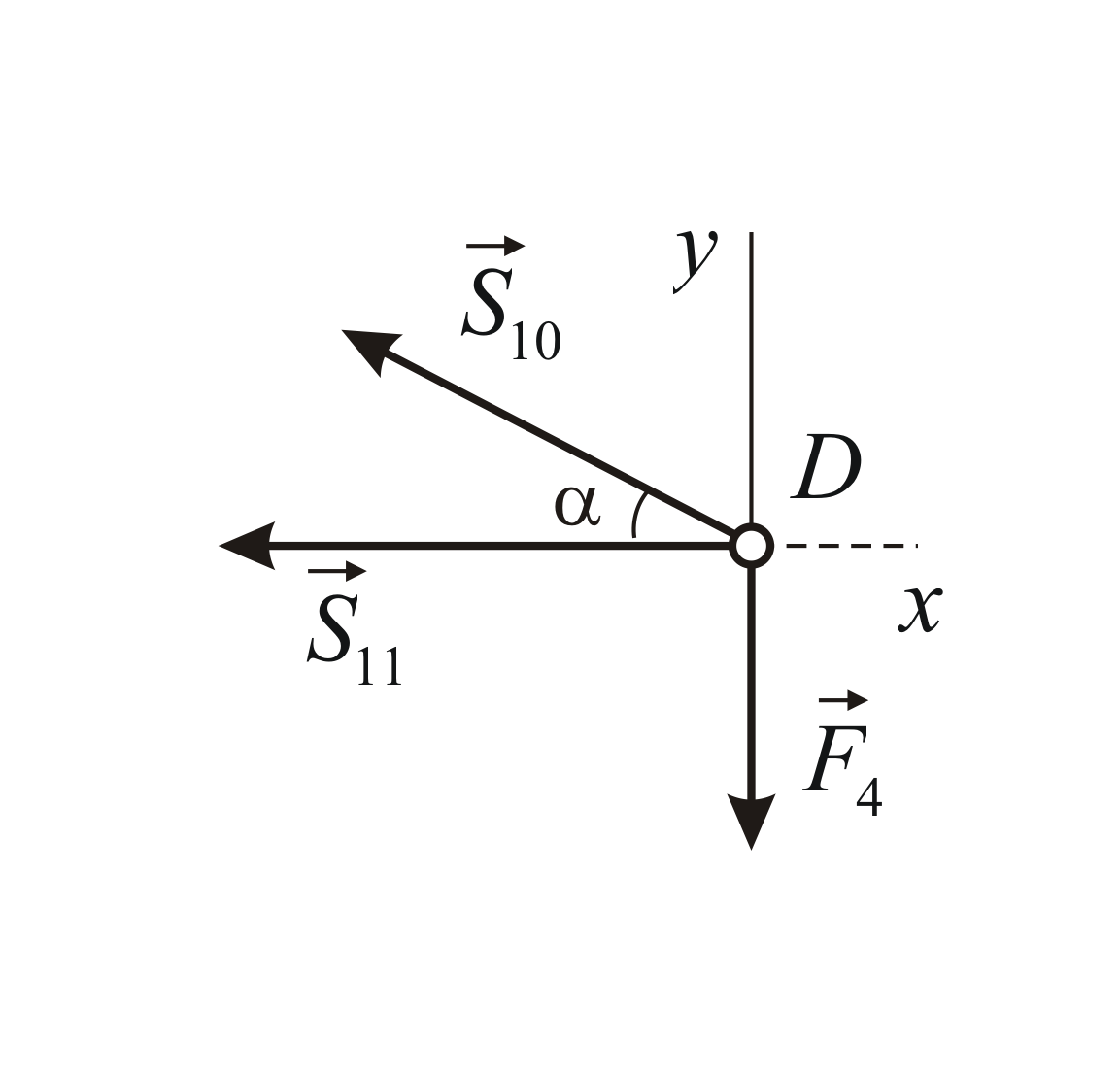 ассмотрим равновесие узла
ассмотрим равновесие узла 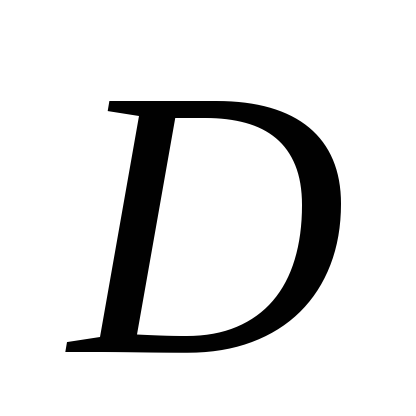
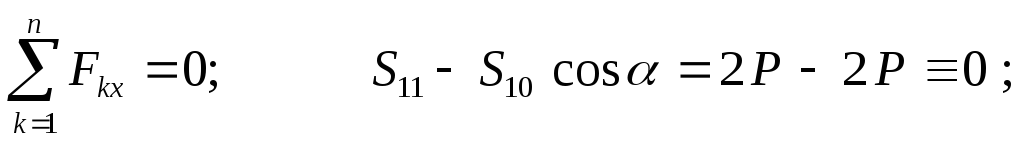
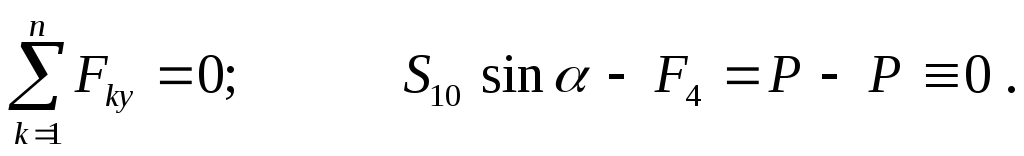
Метод сквозных сечений (метод Риттера).Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчётов. Идея метода состоит в том, что ферма разделяется сечением на две части и рассматривается равновесие одной из этих частей. Сечение проводится по трём стержням фермы, в которых (или в одном из которых) требуется определить усилие. Действие отброшенной части фермы заменяют соответствующими реакциями, направляя их вдоль разрезанных стержней от узлов, т.е. считая стержни растянутыми (как и в методе вырезания узлов). Условия равновесия составляются так, чтобы в каждое уравнение входила только одна неизвестная величина.
Если сечение проводится более, чем по трём стержням, то усилия в «лишних» стержнях должны быть определены предварительно. В противном случае будет необходимо рассмотреть комбинацию из нескольких сечений или комбинацию метода сечений и метода вырезания узлов.
В качестве примера проведём сечение через шестой, седьмой и восьмой стержни. Рассмотрим равновесие правой части фермы (Рис. 2.20).
Уравнения равновесия имеют вид:
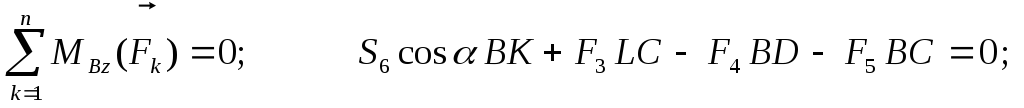
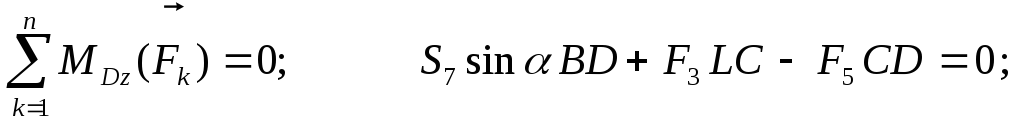
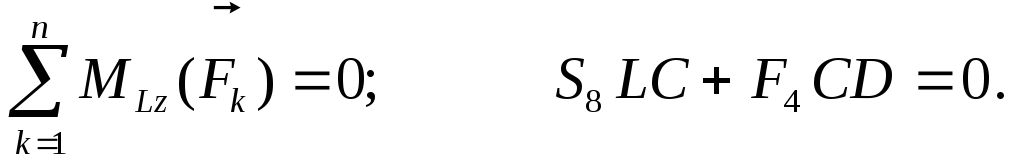
Отсюда:
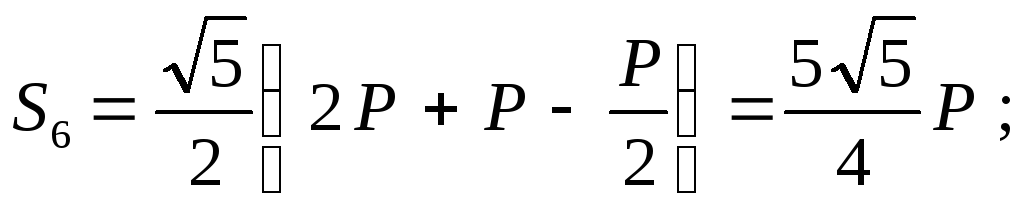
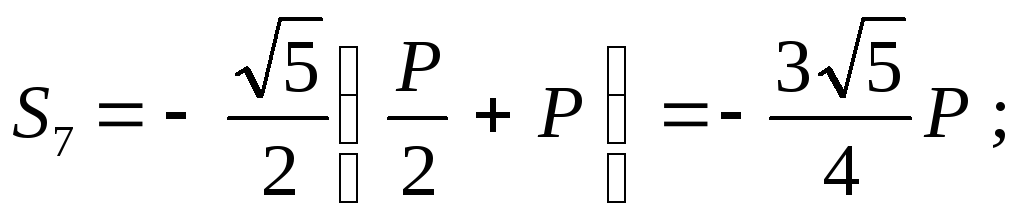
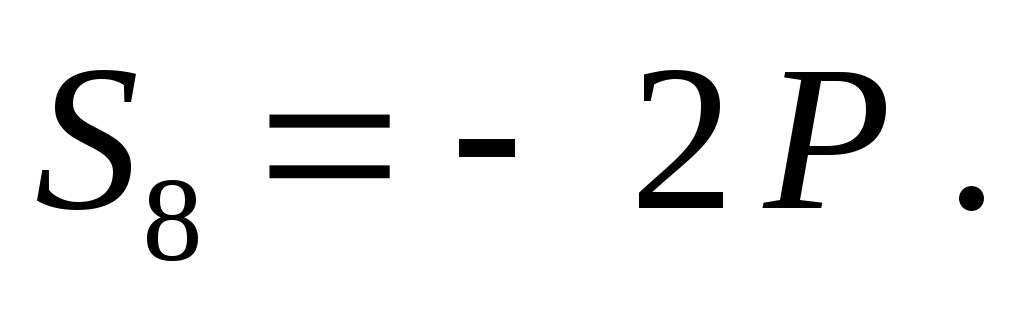
|
Рис. 2.20 |
Условие жёсткости фермы.Найдём
минимальное число стержней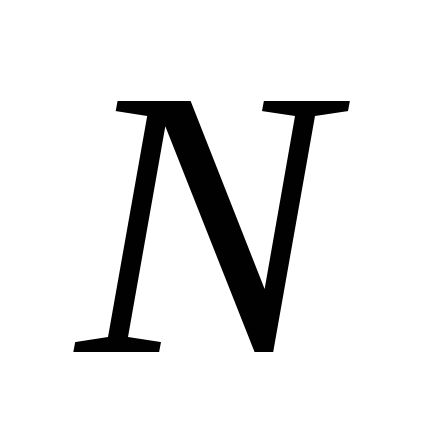 ,
которое необходимо для образования
плоской фермы, имеющей
,
которое необходимо для образования
плоской фермы, имеющей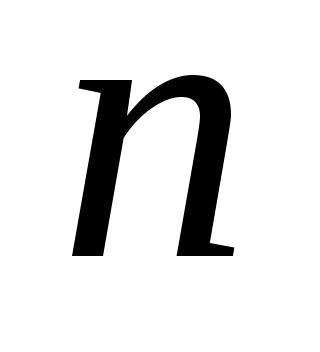 узлов. Простейшая ячейка фермы
(треугольник) имеет три стержня и три
узла. Для присоединения каждого из
оставшихся
узлов. Простейшая ячейка фермы
(треугольник) имеет три стержня и три
узла. Для присоединения каждого из
оставшихся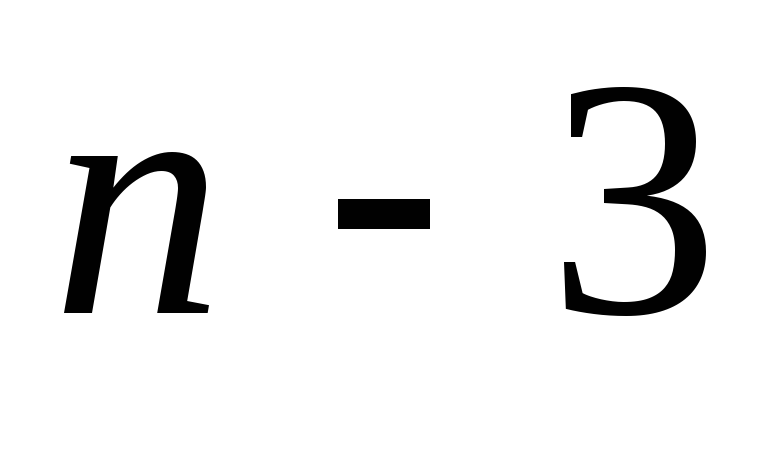 узлов необходимо два стержня. Таким
образом, условие жёсткости фермы имеет
вид:
узлов необходимо два стержня. Таким
образом, условие жёсткости фермы имеет
вид:
Условие статической определимости
фермы.Ферма является статически
определимой, если число неизвестных
совпадает с числом независимых уравнений
равновесия, в которые эти неизвестные
входят. Для плоской фермы, имеющей узлов, можно составить
узлов, можно составить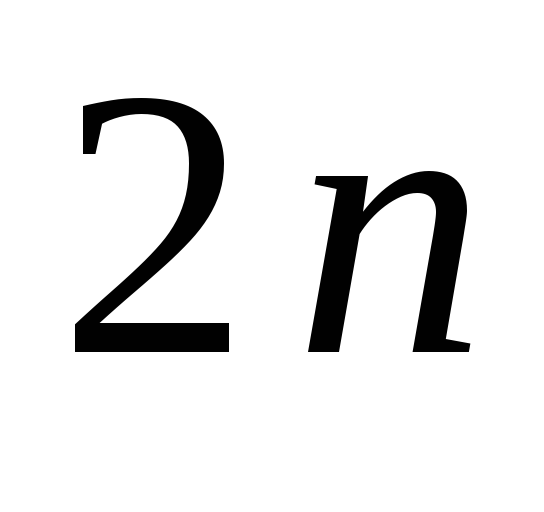 уравнений равновесия, три из которых
расходуются на определение трёх
составляющих реакций опор. Для определения
усилий в стержнях фермы остаётся
уравнений равновесия, три из которых
расходуются на определение трёх
составляющих реакций опор. Для определения
усилий в стержнях фермы остаётся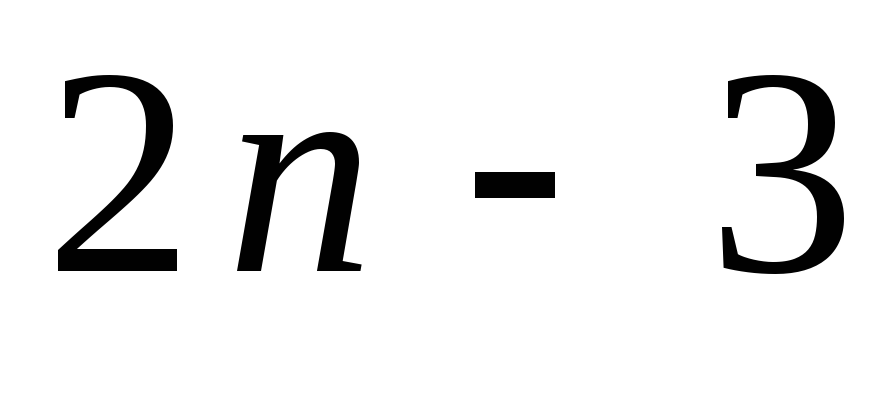 уравнения. Таким образом, условие
статической определимости фермы
совпадает с условием её жёсткости.
уравнения. Таким образом, условие
статической определимости фермы
совпадает с условием её жёсткости.
Методы расчёта фермы рассмотрим на примере.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
В чём суть упрощающих предположений, принимаемых при расчёте фермы?
В чём состоит метод вырезания узлов?
В чём состоит метод сквозных сечений?
Каково условие жёсткости фермы?
Каково условие статической определимости фермы?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 4.66; 4.67; 4.68; 4.70; 4.71; 4.73; 4.74.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА — теория и практика»: комплекты СР-8; СР-9; СР-10; СР-11.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7
Расчет ферм. Понятие о ферме. Аналитический расчет плоских ферм.
Фермой
называется жесткая конструкция из
прямолинейных стержней, соединенных
на концах шарнирами. Если все стержни
фермы лежат в одной плоскости, ферма
называется плоской. Места соединения
стержней фермы называют узлами. Все
внешние нагрузки к ферме прикладываются
только в узлах. При расчете фермы трением
в узлах и весом стержней (по сравнению
с внешними нагрузками) пренебрегают
или распределяют веса стержней по узлам.
Тогда на каждый из стержней фермы будут
действовать две силы, приложенные к
его концам, которые при равновесии могут
быть направлены только вдоль стержня.
Следовательно, можно считать, что стержни
фермы работают только на растяжение
или на сжатие. Ограничимся рассмотрением
жестких плоских ферм, без лишних стержней,
образованных из треугольников. В таких
фермах число стержней 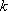 и число узлов
и число узлов связаны соотношением
связаны соотношением
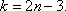
Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях.
Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело. Перейдем к определению усилий в стержнях.
Метод вырезания узлов.
Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Ход расчетов поясним на конкретном примере.

Рис.23
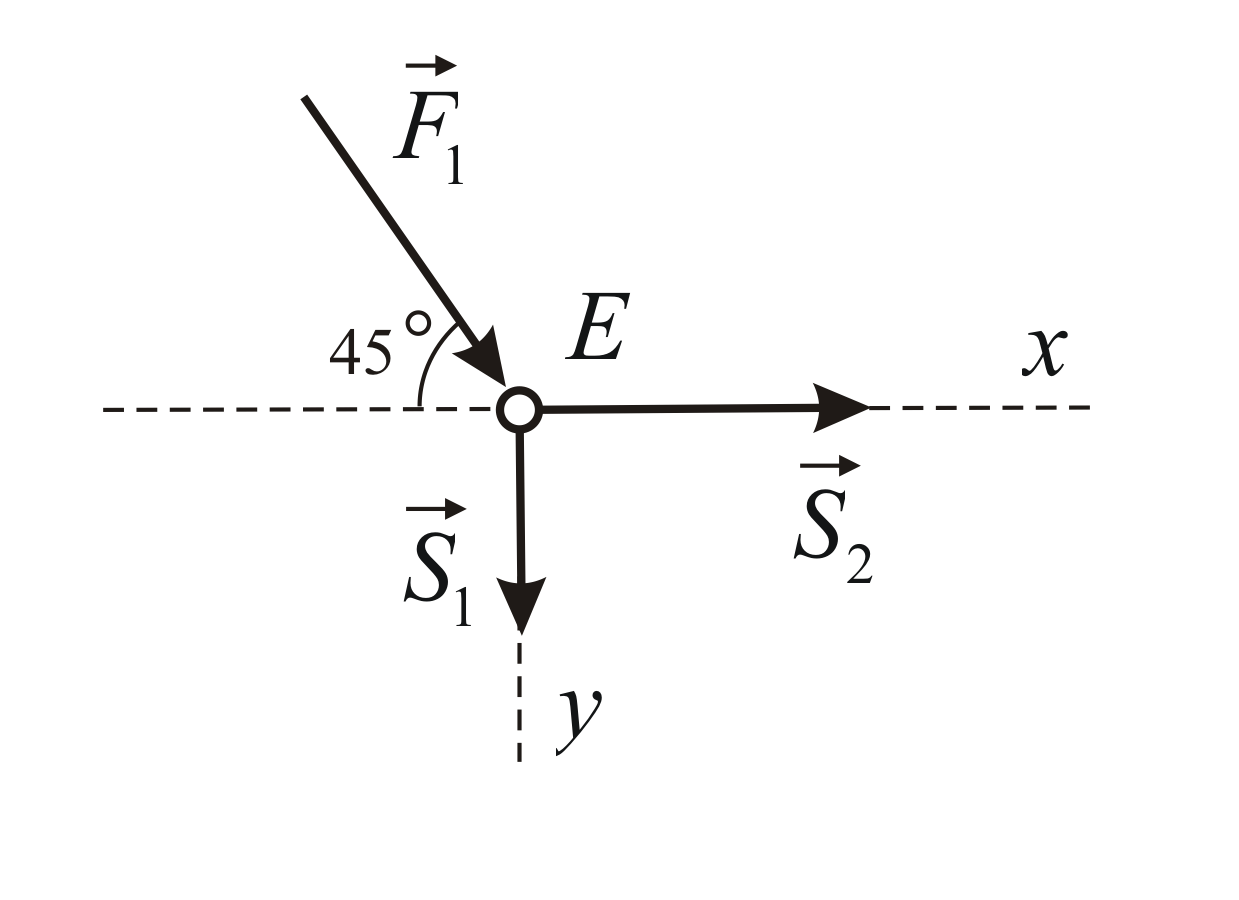
Рассмотрим изображенную на рис. 23,а ферму, образованную из одинаковых равнобедренных прямоугольных треугольников; действующие на ферму силы параллельны оси х и равны: F1 = F2 = F3 = F = 2.
В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соотношение выполняется и ферма является жесткой, без лишних стержней.
Составляя уравнения равновесия для фермы в целом, найдем, что реакции опор направлены, как показано на рисунке, и численно равны;

Переходим к определению усилий в стержнях.
Пронумеруем узлы фермы римскими цифрами, а стержни — арабскими. Искомые усилия будем обозначать S1 (в стержне 1), S2 (в стержне 2) и т. д. Отрежем мысленно все узлы вместе со сходящимися в них стержнями от остальной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям S1, S2, … Изображаем сразу все эти силы на рисунке, направляя их от узлов, т. е. считая, все стержни растянутыми (рис. 23, а; изображенную картину надо представлять себе для каждого узла так, как это показано на рис. 23, б для узла III). Если в результате расчета величина усилия в каком-нибудь стержне получится отрицательной, это будет означать, что данный стержень не растянут, а сжат. Буквенных обозначений для сил, действующих вдоль стержней, ни рис. 23 не вводам, поскольку ясно, что силы, действующие вдоль стержня 1, равны численно S1, вдоль стержня 2 — равны S2 и т. д.
Теперь для сил, сходящихся в каждом узле, составляем последовательно уравнения равновесия
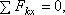
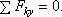
Начинаем с узла 1, где сходятся два стержня, так как из двух уравнений равновесия можно определить только два неизвестных усилия.
Составляя уравнения равновесия для узла 1, получим
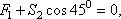
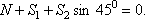
Отсюда находим
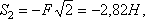
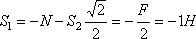
Теперь, зная S1, переходим к узлу II. Для него уравнения равновесия дают
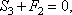
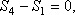
откуда
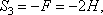
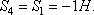
Определив S4, составляем аналогичным путем уравнения равновесия сначала для узла III, а затем для узла IV. Из этих уравнений находим:
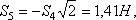
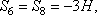
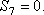
Наконец, для вычисления S9 составляем уравнение равновесия сил,
сходящихся в узле V, проектируя их на
ось By.
Получим 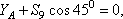 откуда
откуда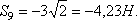
Второе уравнение равновесия для узла V и два уравнения для узла VI можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уравнения равновесия всей фермы в целом при определении N, ХА, и YА.
Окончательные результаты расчета можно свести в таблицу:
№ стержня ………. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Усилие в Н ……… | -1 | -2,82 | -2 | -1 | +1,41 | -3 | 0 | -3 | -4,23 |
Как показывают знаки усилий, стержень 5 растянут, остальные стержни сжаты; стержень 7 не нагружен (нулевой, стержень).
Наличие в ферме нулевых стержней, подобных стержню 7, обнаруживается сразу, так как если в узле, не нагруженном внешними силами, сходятся три стержня, из которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю. Этот результат получается из уравнения равновесия в проекции на ось, перпендикулярную к упомянутым двум стержням.
Если в ходе расчета встретится узел, для которого число неизвестных больше двух, то можно воспользоваться методом сечений.
2.3. Расчет плоских ферм
2.3.1. Основные понятия
Фермой называется строительная конструкция, образованная из прямолинейных стержней, соединенных идеальными (то есть без трения) шарнирами.
Если нагрузка, приложена только в узлах фермы, образованных этими шарнирами, все стержни будут находиться в условиях центрального растяжения или сжатия.
Напомним, что из внутренних усилий для этого вида напряженно-деформированного состояния отличной от нуля может быть только продольная сила: M = 0, Q = 0, N 0.
В рамках строительной механики расчет фермы сводится к определению усилий в ее стержнях, и в дальнейшем, при необходимости, к построению эпюры N.
Рассмотрим два простейших метода определения этих усилий.
2.3.2. Метод сечений
Суть этого метода заключается в следующем: проводят сечение, разбивающее ферму на две части и рассматривают равновесие одной из частей под действием: активных сил, опорных реакций и усилий в разрезанных стержнях как произвольной плоской системы сил.
Для такой системы можно составить три уравнения равновесия, поэтому метод удобен, когда сечение пересекает не более трех стержней.
Если все рассеченные стержни при этом непараллельны, то для определения усилий целесообразно составить уравнения:
SM1 = 0; SM2 = 0; SM3 = 0,
взяв в качестве моментных точки, где пересекаются линии действия реакций двух разрезанных стержней из трех, а если два стержня параллельны, то уравнения:
SM1 = 0; SM2 = 0; SY = 0,
где ось Oy перпендикулярна этим стержням.
Рассмотренный способ определения усилий можно применять и в том случае, если сечение пересекает более трех стержней, однако при этом каждое из усилий уже не удается найти независимо от остальных, поскольку приходится рассматривать равновесие обеих частей фермы, а иногда проводить дополнительные сечения.
При решении все стержни фермы рекомендуется считать растянутыми, направляя усилия от узлов.
Пример 2.6. Найти усилия в указанных стержнях фермы (рис. 2.7, а).
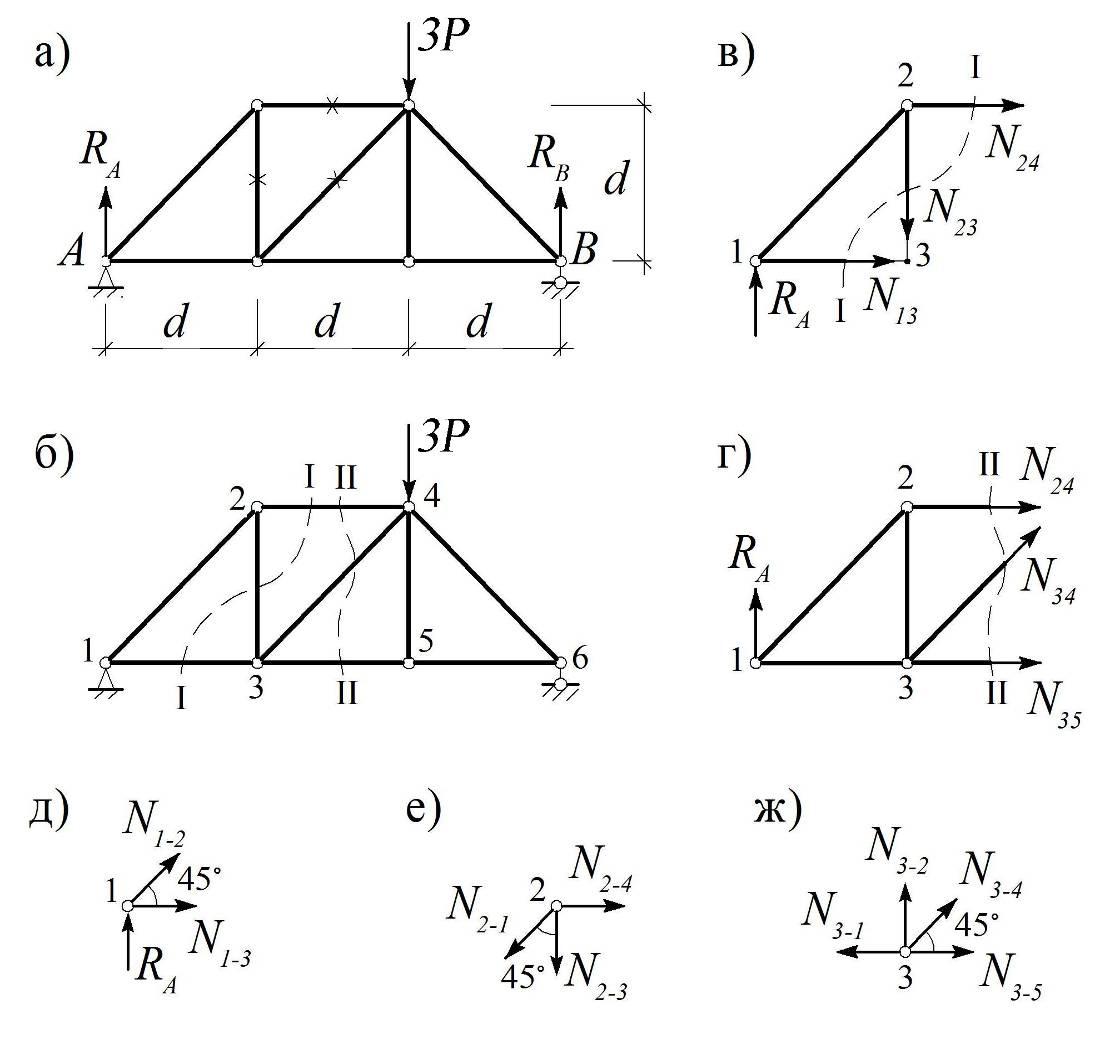
Рис.2.7
Решение. Определяем опорные реакции:
MА = 0; RB = 2P;
MB = 0; RA = P;
Проверка:
Y = RA + RB 3P = 0.
Для определения усилий N2-3 и N2-4 проведем сечение I-I (рис. 2.7, б) и рассмотрим равновесие части фермы, взятой слева от этого сечения. Помимо опорной реакции RA к ней будут приложены неизвестные усилия в разрезанных стержнях: N2-4, N2-3 и N1-3 (рис. 2.7, в).
Чтобы найти усилие N2-4 составим уравнение M3(лев)=0, выбрав в качестве моментной точку, где пересекаются линии действия N2-3 и N1-3:
RA d N2-4 d = 0; N2-4 = RA = P.
Поскольку стержни 2-4 и 3-5 параллельны и перпендикулярны оси Оу, для нахождения N2-3 составляем уравнение:
Y ( лев) = RA N2-3 = 0; N2-3 = RA = P.
Для определения усилия в стержне 3-4 проводим дополнительно сечение II-II, пересекающее этот стержень (рис. 2.7, б) и рассматриваем равновесие части фермы, расположенной слева от этого сечения (рис. 2.7, г):
Y ( лев) = RA + N3-4sin45
= 0; N3-4 = RA / sin45
= P 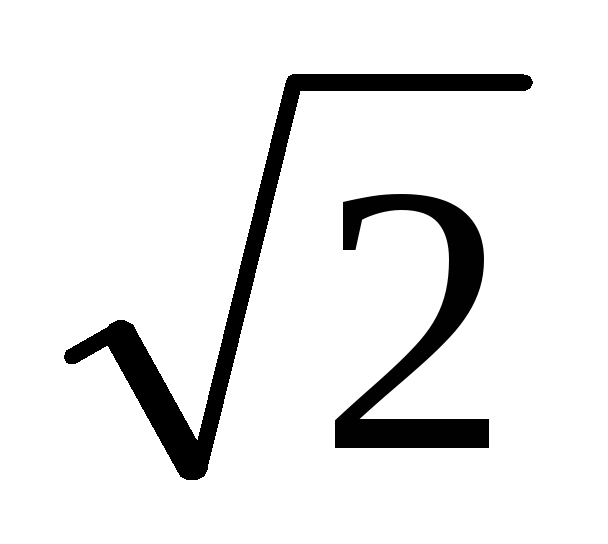 .
.
То же самое усилие можно найти, рассматривая равновесие части фермы не слева, а справа от этого сечения:
Y ( пр) = RВ
3P + N4-3sin45
= 0; N4-3 = N3-4 = P 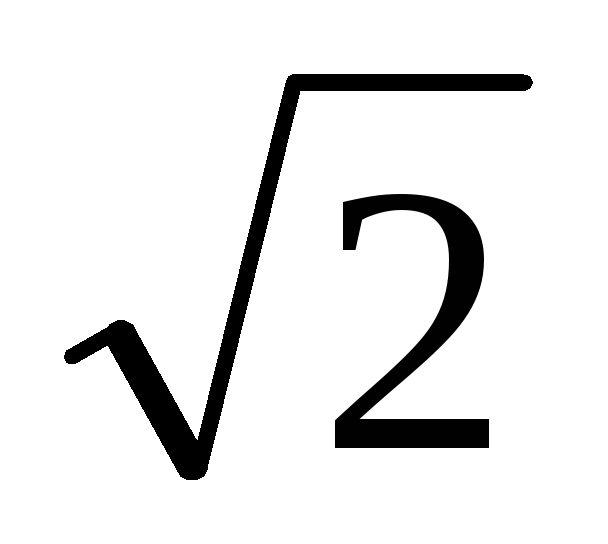 .
.
Аналитические методы расчета ферм
Для расчета простых ферм применяются различные методы. Рассмотрим их на конкретном примере (рис.1).
Метод вырезания узлов.
 Вырежем узел 4 (рис. 1) и рассмотрим
его равновесие (рис 2):
Вырежем узел 4 (рис. 1) и рассмотрим
его равновесие (рис 2):
Σy = s43cos45o + 2F = 0, откуда s43 = –2F/cos45o,
знак (–) показывает, что стержень 3–4 сжат, следовательно, на рис. 2 необходимо изменить направление усилия s43. Затем составляем
Σx = –s42 + s43cos45o = 0, тогда s42 = s43cos45o = 2F.
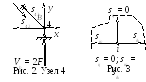 В дальнейшем следует применить
следующий порядок вырезания узлов: узел
3, узелА, узел 1.
В дальнейшем следует применить
следующий порядок вырезания узлов: узел
3, узелА, узел 1.
Если в узле сходятся три стержня, из которых два направлены одинаково и нет нагрузки, то усилие в отдельно направленном стержне равно нулю (рис. 3).
При вырезании узлов необходимо, чтобы число неизвестных усилий в нем не превышало двух.
Метод моментных точек
Проведем сечение I–Iи отбросим левую часть фермы (рис. 1). Для оставшейся части точка 3 будет моментной:
ΣM3 = Vb a – s42 a = 0, тогда s42 = Vb = 2F.
Метод полного сечения (способ проекций)
Рассмотрим сечение I–I. Отбросим левую часть, а для оставшейся части составим условие:
Σy = –s32sin45o – F + Vb = 0, откуда s32 = (–F + Vb)/sin45o = F/sin45o.
Метод двух или нескольких сечений
 Делается два или несколько сечений,
составляются уравнения статики и
совместно решаются.
Делается два или несколько сечений,
составляются уравнения статики и
совместно решаются.
Метод замкнутых сечений
Делается замкнутый разрез, который пересекает некоторые стер-жни два раза. Усилия дважды пересеченных стержней в уравнения статики не войдут (рис. 4). Например, для замкнутого сечения, показанного на рис. 4, имеем:
ΣMА= s3b + Vba = 0,
тогда s3 = Vba/b.
Метод замены стержней
 Путем замены стержней ферма превращается
в простую, которая кладется в основу
расчета. Например, на ферме, показанной
на рис. 5,а, убираем стержень 1–2, а
его влияние заменяем фиктивной внешней
силойХи ставим дополнительный
стержень, усилие в котором обозначим
черезN3. УсилиеХ(рис. 5,б) определяется из
условия, чтоN3=
0. ПоложимХ= 1 и находим
Путем замены стержней ферма превращается
в простую, которая кладется в основу
расчета. Например, на ферме, показанной
на рис. 5,а, убираем стержень 1–2, а
его влияние заменяем фиктивной внешней
силойХи ставим дополнительный
стержень, усилие в котором обозначим
черезN3. УсилиеХ(рис. 5,б) определяется из
условия, чтоN3=
0. ПоложимХ= 1 и находим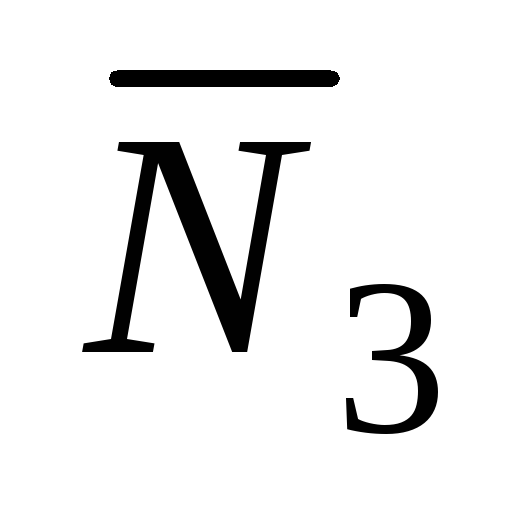 ,
а усилие в фиктивном стержне только от
внешней нагрузки обозначим через
,
а усилие в фиктивном стержне только от
внешней нагрузки обозначим через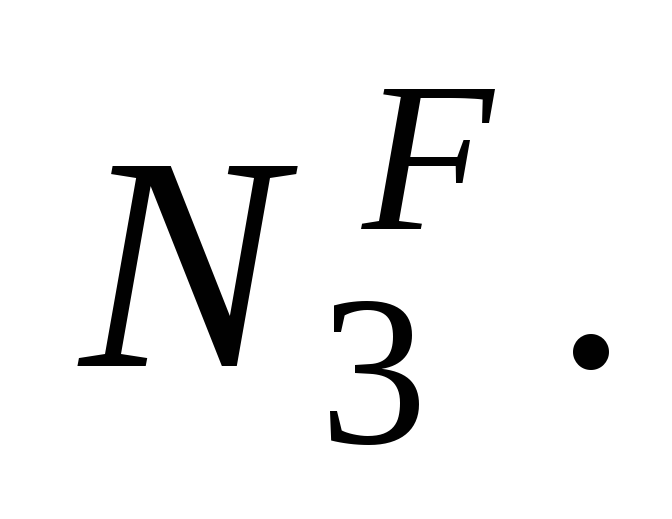 В этом случае запишем:
В этом случае запишем:
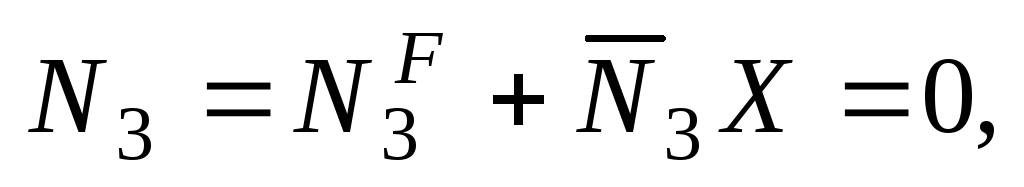
тогда 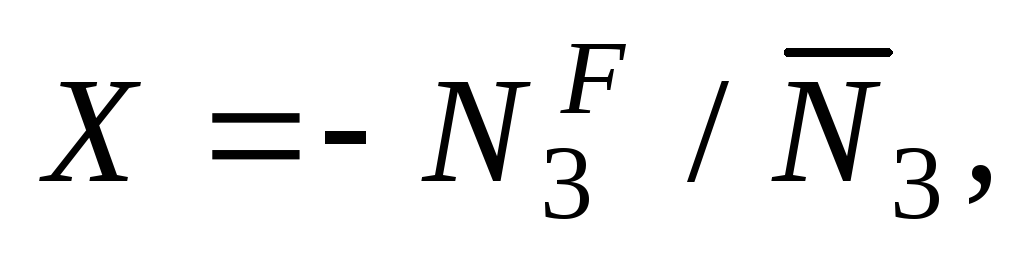 после чего определяем усилия в остальных
стержнях.
после чего определяем усилия в остальных
стержнях.
Л е к ц и я 5
Построение линий влияния усилий в стержнях ферм
 Линия влияния усилия в стержне фермы
представляет собой график изменения
усилия в рассматриваемом стержне, когда
грузР= 1 медленно движется по нижнему
или верхнему поясу фермы без толчков и
ускорений. Тот пояс фермы, по которому
движется единичный груз называетсягрузовым поясом.
Линия влияния усилия в стержне фермы
представляет собой график изменения
усилия в рассматриваемом стержне, когда
грузР= 1 медленно движется по нижнему
или верхнему поясу фермы без толчков и
ускорений. Тот пояс фермы, по которому
движется единичный груз называетсягрузовым поясом.
Рассмотрим ферму, показанную на рис. 1. Для построения линии влияния опорной реакции Rbнеобходимо взять
ΣM1=Rbl–Px= 0, тогдаRb = x/l.
Аналогично запишем
ΣM12=Ral–P(l – x) = 0, откуда
Ra =(l – x)/l.
Для построения линии влияния усилия s75в стержне 5–7 проведем разрезI–I. Предположим, что груз справа от сечения. В этом случае рассмотрим левую часть фермы:
ΣM6 = Ra3d + s75r = 0, поэтому
s75 = –Ra3d/r,
то есть линия влияния s75 для правой части есть линия влиянияRa, умноженная на 3d/rи взятая со знаком (–). Предполагая, что грузР= 1 слева от сеченияI–Iи рассматривая равновесие правой части фермы, находим
ΣM6 = Rb3d + s75r = 0, откуда
s75 = –Rb3d/r.
Сечение I–Iможно использовать для построения линии влияния усилияs56. Если единичный груз справа от сечения, то из рассмотрения левой части фермы определяем:ΣM1=s56c= 0 иs56= 0.
Если груз Р= 1 слева от сечения, то рассматривая правую часть, получаем
Σ M1 = Rbl + s56c = 0, тогда s56 = –Rbl/c.
M1 = Rbl + s56c = 0, тогда s56 = –Rbl/c.
Для построения линии влияния усилия s76 в стержне 6–7 вырежем узел 7 (рис. 1) и рассмотрим его равновесие (рис. 2) при условии, что грузовой пояс – нижний:
Σx = s75cosα – s79cosα = 0,
поэтому s75 = s79;
Σy = –s76 + (s75 + s79)sinα = 0,
откуда s76= 2s75sinα, то есть ли-ния влияния усилияs76 есть ли-ния влияния усилия s75, умноженная на 2sinαи взятая со знаком (+), т.к. в стержне 6–7 – растяжение.
Построим несколько линий влияний усилий в стержнях фермы с параллельными поясами, показанной на рис. 3.
Линия влияния усилия s46.
Пусть грузовым является верхний пояс. Проведем сечение I–I. Груз – справа, рассмотрим левую часть:
ΣM5 = Ra12 + s464 = 0,
тогда s46 = –3Ra.
Груз – слева, рассмотрим правую часть фермы:
ΣM5 = Rb24 + s464 = 0,
тогда s46 = –6Rb.
Аналогично строится линия влияния усилия s46 при нижнем грузовом поясе, только в левую часть фермы входит участок от узла 0 до узла 5, а в правую часть – от узла 13 до узла 7.
Линия влияния усилия s45. Грузовой пояс – верхний. Проведем сечениеII–II. Груз – справа, рассмотрим левую часть:
Σy = Ra – s45cosα = 0, тогда s45 = Ra /cosα = 5Ra /4.
Груз слева, рассмотрим правую часть:
Σy = Rb + s45cosα = 0, поэтому s45 = –Rb /cosα = –5Rb /4.
При езде по нижнему поясу передаточная прямая будет в пределах участка 3–5.
Л е к ц и я 6