Прогиб балки онлайн калькулятор: Расчет балки на прогиб и прочность

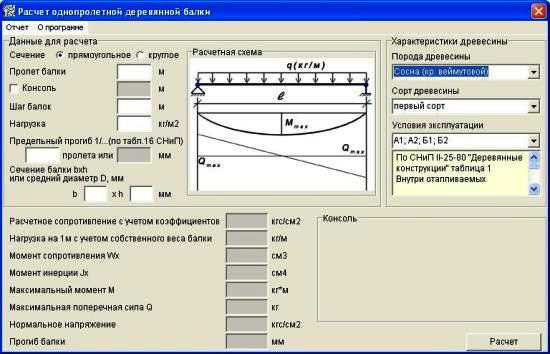
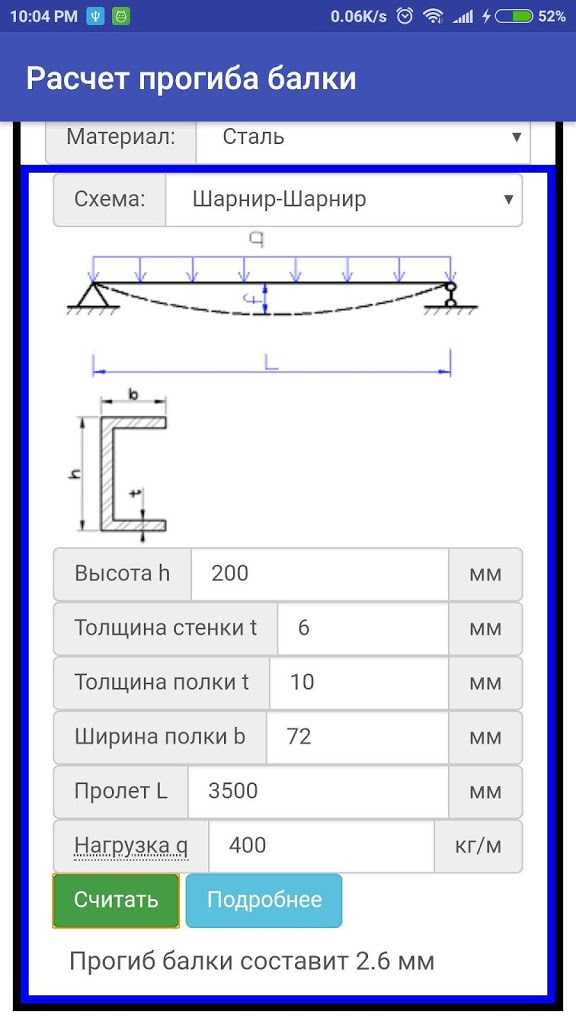
Расчет балки на изгиб — Favorit-TK.ru

Рассчитывать балку на изгиб можно несколькими вариантами:

1. Расчет максимальной нагрузки, которую она выдержит
2. Подбор сечения этой балки
3. Расчет по максимальным допустимым напряжениям (для проверки)

Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.

Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент. Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.

После нахождения изгибающего момента мы должны найти момент сопротивления Wx этого сечения по формуле приведенной в таблице:

Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.

Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала, а для хрупких (чугун) – пределу прочности. Предел текучести и предел прочности мы можем найти по таблицам ниже.

1. Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.

Для начала нам необходимо выбрать расчетную схему.

На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине, то и максимальное напряжение будет в заделке.

Давайте найдем его:
P = m * g = 90 * 10 = 900 Н = 0.9 кН
М = P * l = 0.9 кН * 2 м = 1.8 кН*м

По таблице сортамента двутавров находим момент сопротивления двутавра №10.
Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.
Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.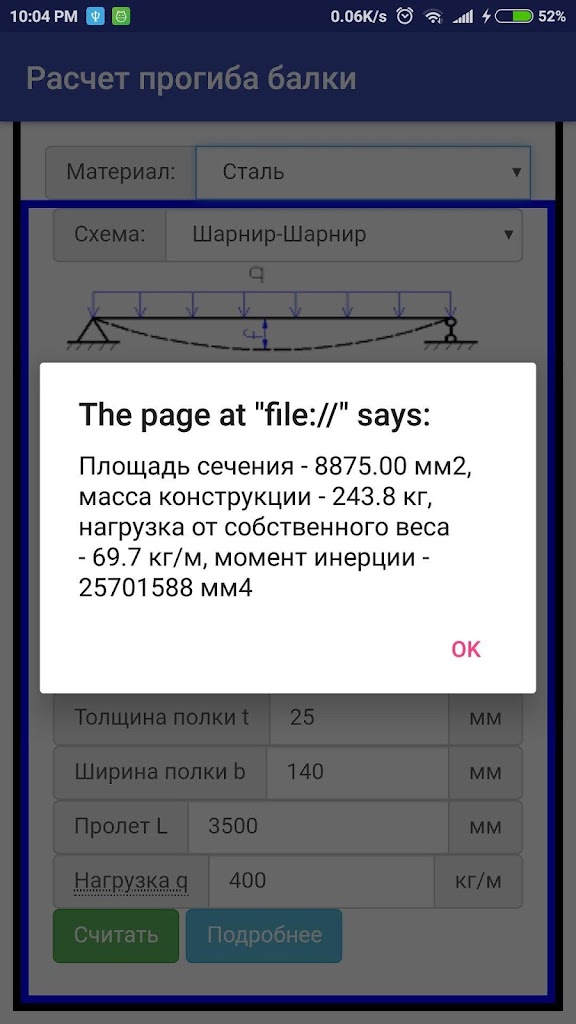
б = М / W = 1.8 кН/м / 0.0000397 м3 = 45340 кН/м2 = 45.34 МПа

После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.
45.34 МПа < 245 МПа – верно, значит данный двутавр выдержит массу 90 кг.

2. Поскольку у нас получился довольно-таки большой запас, то решим вторую задачу, в которой найдем максимально возможную массу, которую выдержит все тот же двутавр №10 длиной 2 метра.

Если мы хотим найти максимальную массу, то значения предела текучести и напряжения, которое будет возникать в балке, мы должны приравнять (б=245 Мпа = 245 000 кН*м2).

Далее по формуле б = М / W, находим максимальный момент.
М = б * W = 245 000 * 0.0000397 = 9.73 кН * м

Тогда по формуле M = P * L найдем P:
P = 9,73 кН/м / 2м = 4,87 кН = 487 кг

Итак, максимальная масса, которую выдержит двутавр №10 – 487 кг.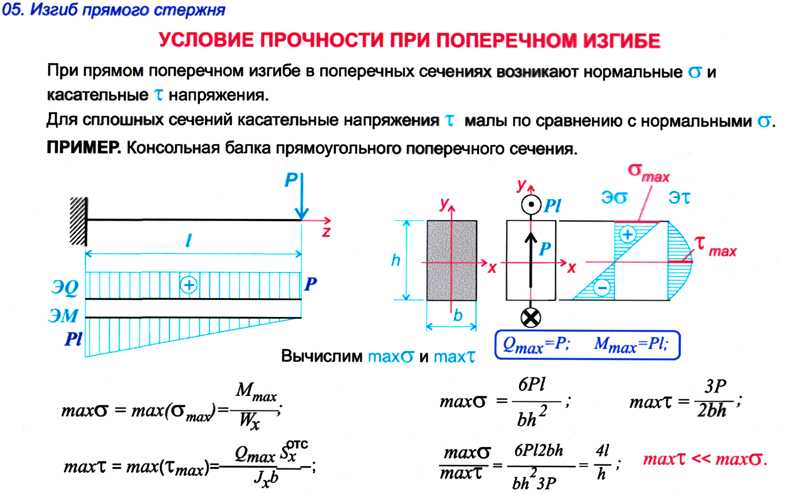 Число это грубое, поскольку для простоты расчета мы не учитывали различные коэффициенты запаса, поэтому, чтобы подстраховаться, возьмите некий двукратный запас по прочности.

Расчет балки на прогиб: формулы и пример расчета

Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Виды балок

Независимо от того, какой должна быть конструкция, материал для изготовления балок выбирают прочный и надежный. Отличаются они друг от друга лишь по своим параметрам:

1. длине;
2. форме;
3. сечению.

Чаще всего, для изготовления балок используется дерево и металл. Расчет балки на изгиб напрямую зависит от выбранного материала. В данном случае большое значение имеют такие показатели как однородность и структура.

Балки из дерева

Конструкции из дерева используются в одноэтажных домах или небольших домиках. Они отлично подходят как для потолка, так и пола. Для расчета прогиба балки берут следующие величины:

1. Тип материала. Каждое дерево отличается прочностью, твердостью и гибкостью.
2. Геометрические показатели, в которые включается как форма изделия, так и его сечение.
3. Предполагаемые нагрузки, которые будут давить на материал.

На то, как будет изгибаться балка учитывается не только реальное давление, но и все возможные силы воздействия.

Стальные балки

Эти изделия очень сложные не только по сечению, но и по составу. Так как из выливают из нескольких видов металла. Производя расчет нагрузки на балку, необходимо принимать во внимание насколько она жесткая, а так же прочно ли она соединена.

Балки из стали используют для строительства многоэтажных домов Источник i0.photo.2gis.com

Конструкция из металла между собой соединяется с помощью:

• сваривания;
• склепывания;
• с помощью соединителей, имеющих резьбу.

Прочные металлические балки используются для строительства домов в несколько этажей. В таких конструкциях вся нагрузка равномерно распределяется по всей балке.

Смотрите также: Каталог проектов домов с террасой.

Прочность и жесткость балки

Балки в доме

Современные строительные технологии, применяемые для просчета стройконструкций, называемых также стержневыми, по качествам прочности и жесткости дают уникальную возможность на первом же этапе проектировки вычислить величину прогиба.

Кроме этого, можно, опираясь на рассчитанные данные, составить заключение о вероятности использования строительной конструкции.

Какой вопрос позволяет решать указанная далее формула для расчета жесткости? Данные, полученные таким путем, говорят о самых больших изменениях в геометрии детали, что могут возникнуть в строительной конструкции.

Несмотря на некоторую бюрократизацию методик для вычисления прогиба, используются опытные формулы, а если воздействие реальных нагрузок отличается от идеальных или усредненных, вопрос решается введением дополнительных коэффициентов для запаса прочности. Понятия «жесткость» и «прочность» связаны и абсолютно неразделимы.

Хотя некоторые различия все-таки есть. Но только в том случае, если рассматривать данные показатели в автомашинах. В стройконструкциях главное нарушение конструкции объектов случается потому, что снижаются или нивелируются полностью вопросы, связанные с запасом прочности, вследствие чего здания нельзя эксплуатировать.

Деревянные балки из древесины хвойных пород

На сегодня в таких предметах изучения, как «Сопромат» и другие, приняты 2 метода для расчета прочности и жесткости:

• Простой. При просчитывании показателей на основе этого метода используют увеличенный коэффициент.
• Точный. Тут используются не только коэффициенты, показывающие запас прочности, но также осуществляется вычисление пограничного состояния (какую нагрузку может выдержать балка).

Как добиться прочности конструкции

Согласно нормам, балка, используемая на эстакаде должна иметь изгиб не больше одного см при ее длине в полтора метра. При этом, в других конструкциях этот показатель меняется. В индивидуальном доме, балки чердака могут прогибаться на один см, при длине 2 м, а в многоэтажных домах тот же сантиметр должен припадать на длину в 2,5 м.

Для того, чтобы постройка была надежной и прочной, расчеты нужно проводить еще в процессе планирования здания. Именно в этот момент и определяется такой показатель, как изгиб балки. Ведь чем меньше прогибается балка, тем выше прочность дома. Таким образом потолок получает равномерное распределение веса и сохраняет устойчивость дома. Если же балки сильно прогибаются, то и весь потолок будет ненадежным и со временем происходит разрыв соединений и здание рушится.

Перед началом расчета, составляют схему давления на балку – макет будет кстати Источник pouznaval.ru

Расчеты проводятся с помощью одного из способов:

1. Прибегнуть к помощи онлайн-калькулятора. В данном инструменте запрограммированы стандартные данные.
2. Воспользоваться справочником и, сравнив все параметры, произвести расчеты самостоятельно.
3. Воспользоваться формулой и самостоятельно просчитать изгиб балок.

Важно! Просчитывать изгиб балки очень важно, чтобы на практике здание было прочным и надежным.

В помещении, которое используется уже не один год, определить насколько аварийным является его состояние, можно только после того, как будет определен уровень проседания балок.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

• Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
• Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
• Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

К сведению! Чтобы реально представлять, почему так важно знать величину отклонения от первоначального положения, стоить понимать, что измерение величины прогиба является единственным доступным и достоверным способом определить состояние балки на практике.
Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Формулы для определения изгиба балки

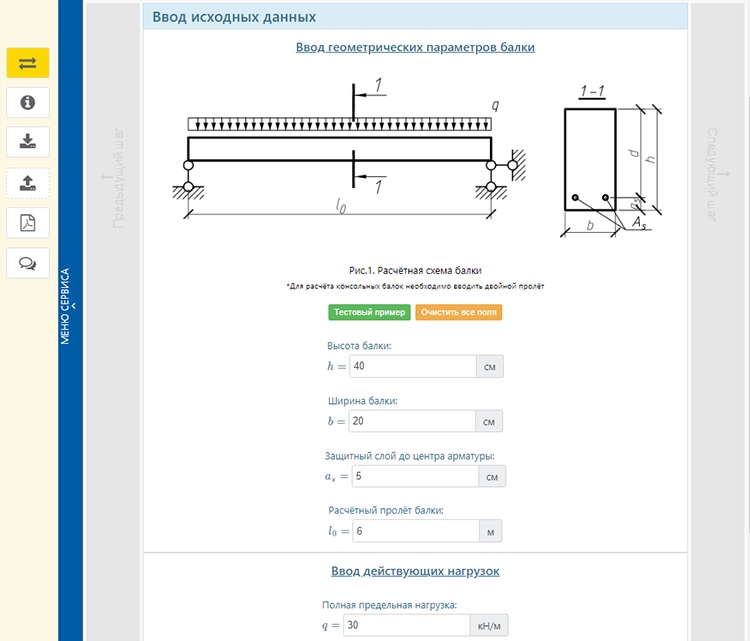
При расчете необходимо учесть силу сопротивления материала, из которого изготовлена конструкция. И только после этого рисуется схема, где указывается сила давления на балку.

Таким образом происходят измерения для вычисления изгиба Источник novainfo.ru

Смотрите также: Каталог компаний, что специализируются на монтаже печей и каминов.

Процесс расчета выглядит следующим образом:

1. Используя формулу площади прямоугольной фигуры S=b*h, определяется сечение балки, а так же берется ко вниманию ее длина L;
2. На балку воздействует сила давления Q, которая изгибает ее в центре, а ее концы образуют угол θ. Обязательно учитывается изначальное положение конструкции f;
3. В схеме концы импровизированной балки установлены совершенно свободно, при этом опоры установлены стационарно. В этом случае нет реакции, как в случае горизонтального закрепления конструкции, и концы балки перемещаются в свободном направлении.

Изгиб предмета под давлением определяется формулой Е=R/Δ. В этом случае Е – это показатель, который берется из справочника, R – сила давления на предмет, Δ – это показатель, который получается в процессе изгиба.

Имея все необходимые показатели можно узнать, какой будет инерция, для этого используется формула:

Δ = Q/(S·Е)

Если же нагрузка будет равномерна по всей длине балки. То нужно использовать такую формулу:

Δ = q·h/(S·Е).

После всех этих вычислений, приходит черед к определению изгиба по системе Юнга. То есть, балку изгибают таким образом, что ее концы выворачиваются в разные стороны, при этом имеют разные куты изгиба. В таком случае в формуле обе части нужно умножить на число L и тогда получается следующее равенство:

Δ*L = Q·L/(b·h·Е)

Формулы можно найти в справочнике Источник pol-exp.com

Как вычислить вспомогательные величины

Для получения полной информации о значениях, необходимых для достижения конечной цели вычислений, нужно узнать, каков момент сопротивление сечения (формула № 2):

Wn(требуемое) = М мах / (Ry * Уc)

Необходимо обязательно уитывать ориентирование рассматриваемого балочного сечения, так как с уменьшением моментов инерций жесткость балок снижается, чего допускать нельзя. Для выяснения максимального значения нагрузки f, которое может выдержать балка, надо вычислить его по такой формуле № 3:

f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦], где

• L – продольный размер, в метрах
• E – коэффициент, показывающий упругость (для каждого материала или сплава он будет разным)
• J – момент инерции по сечению
• qn – это нагрузка, равномерно-распространенная, выражается в кг/м или в Н/м

Показатель J рассчитывается так:

J = b * h4 / 12

Обозначения:

• b – диаметр сечений
• h – вертикальный размер сечения

Примером для сечений, величиной 15 на 20 сантиметров:

J = 0,15 * (0,2)3 / 12 = 10 000 см4 или 0,0001 м4

Кроме указанных расчетных или табличных величин, среди важных факторов, которые нужно учитывать при определении максимальных нагрузок, выделяют такие: статические (которые действуют постоянно, независимо от переменных внешних факторов), периодические (действие ветра, вибрации, ударов).

Дополнительные функции двутавра в частном домостроении

Сама перекрытие вовсе не обязательно должно состоять только из металлических двутавровых балок. Нередко их используют только в самых напряженных местах, а между металлическими частями устанавливают деревянные двутавры.

Почему так? Дело в том, что для сварки нужна высокая квалификация рабочих. Далее, в обычной литературе и интернет-сайтах нет того многообразия узлов и готовых схем конструкции для установки такого перекрытия, здесь действительно требуется грамотный инженер, и даже мы даем только рекомендации. Кроме того, металл обходится недешево. Да и качество сварки очень важно. Она должна работать долго, даже в условиях коррозии или перемены нагрузок.

Поэтому вот такой вариант не только имеет право на жизнь, но и достаточно практичен:

И, наконец, металлическая двутавровая балка нередко служит дополнительным функциональным элементов, который в любом хозяйстве имеет ценность:

Что собой представляет сварной двутавр?

По своему типу сечения двутавровые металлические балки сегодня принято делить на прокатные или составные, которые называются еще сварными. Сварная двутавровая балка – это особый вид фасонного металлического проката в форме наклонного или горизонтального бруса. Изготавливают ее сегодня из углеродистой и низколегированной стали, обязательно высокого качества.

Давайте перечислим основные преимущества двутавровых сварных балок:

• Перекрывают большие пролеты со значительным нагрузками.
• Идеально перераспределяют горизонтальные и вертикальные нагрузки.
• Прекрасно работают на изгиб благодаря жесткости профиля балки.
• Не горят и не теряют свою несущую способность при нагревании даже достаточно высокими температурами.
• Устойчивы к биологическим воздействиям.
• Отлично подходят для строительства конструкции быстровозводимых зданий.
• Позволяют значительнее снизить массу всей конструкции, по сравнению с горячей корнями.
• Изготавливаются также с полностью ассиметричным сечением.

Вот почему такие сварные балки используются сегодня и в строительстве жилых домов, и для промышленных комплексов, и даже для мостов и тоннелей. Казалось бы, что такая балка будет слишком тяжелой для частного домостроительства, но на самом деле применение стальных двутавров позволяет в итоге сократить общий вес несущих конструкций. Но помните, что в отношении к перекрытию из сварных стальных двутавров существуют свои строгие требования:

Классические ошибки

Инженеры, не имеющие должного опыта, часто допускают некоторые ошибки при расчёте балок, а именно:

1. 
   Слишком малое сечение, даже если оно и проходит по условиям прочности, может прогнуться больше нормативных значений, из-за чего перекрытие перестанет удовлетворять эксплуатационным требованиям.
2. Наоборот, слишком большое сечение приведёт к перерасходу материалов и повышенным затратам при строительстве.
3. Неверно выбранное защемление балки повлияет на результат расчёта.
4. При расчёте необходимо приводить все единицы к единому модулю, а, в противном случае, результат окажется далёким от истины.

Чтобы не совершать типичные ошибки, следует выполнять расчёт в соответствии с алгоритмом и фиксировать все промежуточные результаты. После выполнения расчёта следует несколько раз проверить результат. Если возникают сомнения, лучше сравнить подобранное сечение балки с аналогичными примерами.

СОДЕРЖАНИЕ

• 1 Прогиб балки при различных нагрузках и опорах 1.1 Консольные балки 1.1.1 Консольные балки с торцевыми нагрузками
• 1.1.2 Равномерно нагруженные консольные балки

1.2 Балки с простой опорой

1.2.1 Простые балки с центральной нагрузкой

1.2.2 Простые балки со смещенной центральной нагрузкой

1.2.3 Равномерно нагруженные простые балки

1.3 Изменение длины

2 единицы

2.1 Международная система (SI)

2.2 Обычные единицы США (США)

2.3 Другое

3 структурный прогиб

4 См. Также

5 ссылки

6 Внешние ссылки

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму.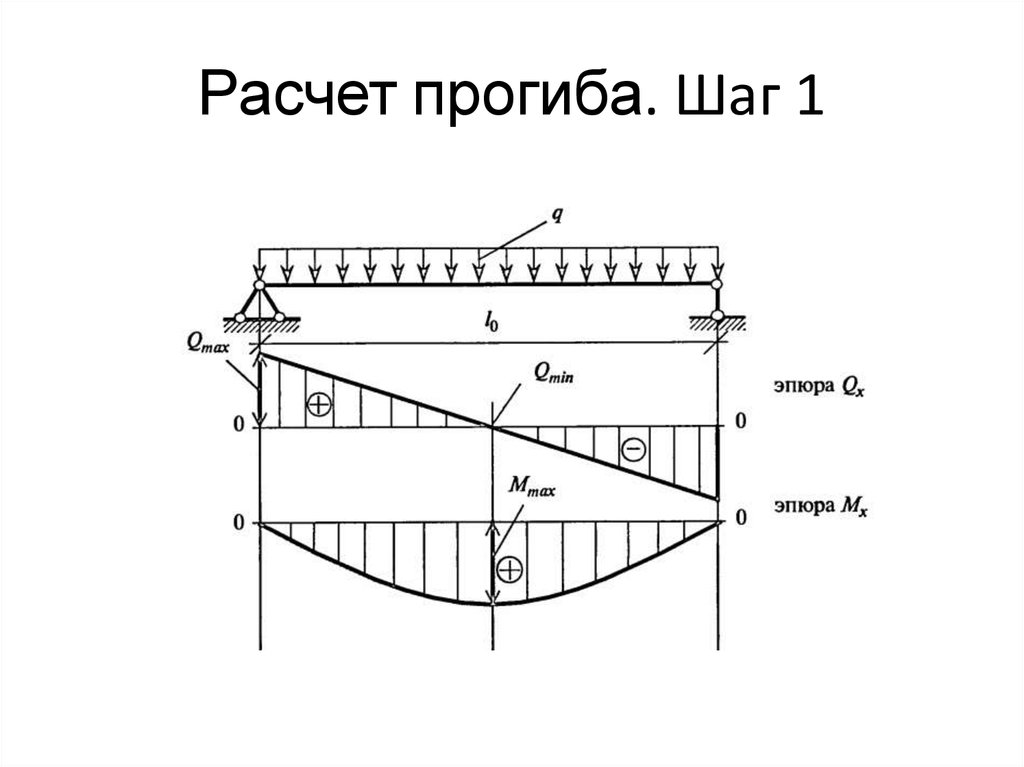 Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и обозначение системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.

Универсальное уравнение прогибов для балки

После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:

• E – модуль упругости;
• I – момент инерции;
• Vk – прогиб сечения K;
• VO – прогиб сечения O;
• θO – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.

Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае Vk, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIVO:

Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθO всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.

Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.

Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24.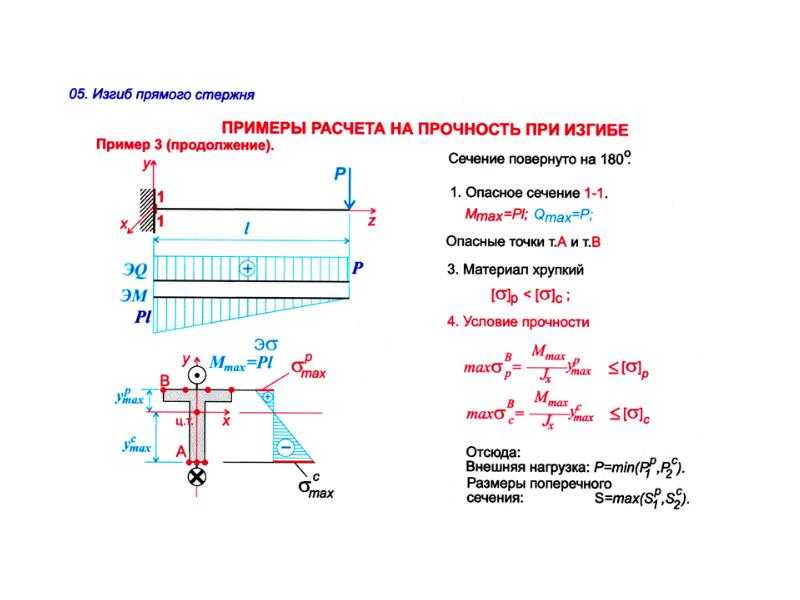 Правило знаков такое же, как и для сосредоточенных сил:

Граничные условия

Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: VK, VO и θO. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть VO=0 и θO=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах.

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.

Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Калькулятор уравнений прогиба и напряжения для консольной балки с равномерной нагрузкой

Калькулятор уравнений прогиба и напряжения для консольной балки с равномерной нагрузкой

Формула прогиба и напряжения балки и калькуляторы

Расчет площади и уравнения инерции

Уравнения момента и инерции

Прогиб балки, напряжение, уравнения изгиба и калькулятор для консольной балки с равномерной нагрузкой.

Открыто
Луно -лучевой лучевой и напряжение на стрессе с однородным калькулятором нагрузки

---

Напряжение луча в определенной точке

Напряжение луча при опор (должна быть постоянная поперечная сечение)

---

Отклонение луча в определенной точке

---

. Отклонение балки в У определенной точке

---

. В определенной точке

---

.

---

Прогиб балки на неподдерживаемом конце, при общей нагрузке «W»

или

Прогиб балки на неподдерживаемом конце, при нагрузке от давления в линии «p»

---

Где:

E =	Модуль упругости	фунтов на кв. дюйм	(Н/мм 2)
Я =	Момент инерции	в 4	(мм 4)
Вт =	Общая нагрузка на балку (не линейная нагрузка)	фунтов	(Н)
р =	С линейной нагрузкой давления	фунтов на квадратный дюйм	(Н/мм)
с =	Напряжение в оцениваемом поперечном сечении	фунт/дюйм 2	(Н/мм 2)
у =	Прогиб балки	дюймов	(мм)
х =	Некоторое расстояние, указанное	дюймов	(мм)
Z =	модуль поперечного сечения балки = I/z	в 3	(мм 3)
г =	расстояние от нейтральной оси до крайнего волокна (края)	дюймов	(мм)
=	Длина указана	дюймов	(мм)

• Обратите внимание, буква «» (строчная буква «L») отличается от буквы «I» (момент инерции).
• Прогиб относится только к постоянным поперечным сечениям по всей длине.

Ссылки:

• Справочник по любому машинному оборудованию, опубликованный с 1931 г. или
• Справочник по машинному оборудованию, 21-е издание, стр. 407 или
• Справочник по машинному оборудованию, 23-е издание, стр. 263 или
• Справочник по машинному оборудованию, 27-е издание, стр. 264

Связанные

• Уравнения прогиба, сдвига и напряжения балки и калькулятор для балки, поддерживаемой одним концом, консольно с обратной конической нагрузкой
• Уравнения прогиба балки, сдвига и напряжений и калькулятор для балки, поддерживаемой одним концом, консольно с ограниченной конической нагрузкой
• Уравнения прогиба балки, сдвига и напряжения и калькулятор для балки, поддерживаемой одним концом, консольно с реверсивной ограниченной конической нагрузкой
• Балка с опорой на один конец, штифт на противоположный конец и частичная распределенная нагрузка Уравнения прогиба, сдвига и напряжения и калькулятор
• Балка поддерживается одним концом, штифтом на противоположном конце и двумя отдельными частями с распределенной нагрузкой.
• Теории хрупкого разрушения Вычисление коэффициентов безопасности Табличный калькулятор Excel
• Уравнения и калькулятор для балки, поддерживаемой одним концом, штифтом на противоположном конце и одной конической распределенной нагрузкой

Калькулятор для инженеров — уклон и прогиб кантилевера

Калькуляторы CE > Уклон и прогиб кантилевера

Калькулятор уклона и прогиба кантилевера

Этот бесплатный онлайн-калькулятор разработан для рассчитать наклон и прогиб в любой точке консольной балки, несущей точечная нагрузка, момент, равномерно распределенная нагрузка (UDL) или равномерно переменная нагрузка (UVL). Он также дает значения максимального наклона и прогиба, которые происходят на свободном конце. Эти калькуляторы основаны на стандартных формулах для наклона и прогиба кантилевера и рекомендованы профессорами университетов.

В случае комбинации нагрузок можно применить принцип суперпозиции для расчета результирующего наклона и прогиба

Этот калькулятор также можно использовать для нахождения ординаты диаграммы влияния для структуры.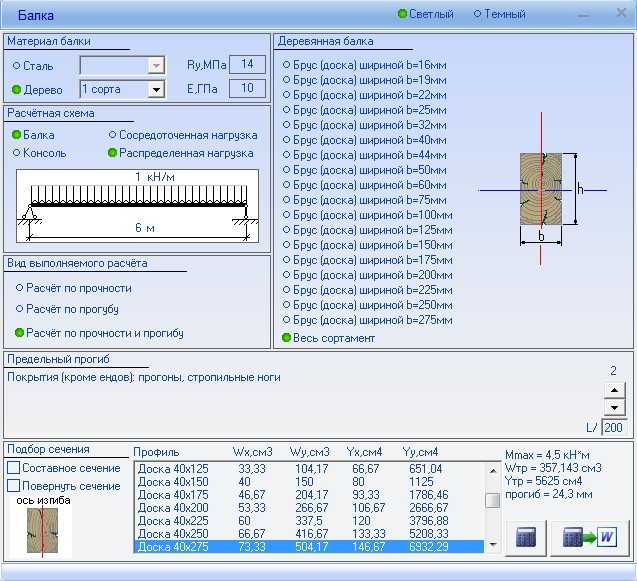

Вы можете выбрать один из вариантов нагрузки, приведенных ниже, или перейти к Инструкции по наклону и прогибу консоли для получения дополнительной информации

Варианты нагрузки для консоли

Точечная нагрузка на консоль

UDL на полном пролете

УДЛ на левой части пролета

УДЛ на правой части пролета

Равномерно изменяющаяся нагрузка (максимальная на фиксированном конце)

Равномерно изменяющаяся нагрузка (максимальная на свободном конце)

Момент на пролете

Скоро будет добавлено больше. Оставайтесь на связи

Вы также можете посетить следующие полезные ссылки

Задача 6-1 Расчет наклона и отклонения кантилевера по методу Маколея

Задача 6-2 Наклон и прогиб простой балки методом двойного интегрирования 902

Проба 7-3 Прогиб балки по методу единичной нагрузки

Проба 7-5 Прогиб фермы с шарнирным соединением по методу единичной нагрузки

Проба 7-1 Решение неопределенной конструкции методом последовательной деформации

Отличные калькуляторы

Калькулятор трансформации напряжения
Расчет главного напряжения, максимального напряжения сдвига и их плоскостей

Калькулятор абсолютного макс. . Б.М. из-за движущихся грузов.

Калькулятор изгибающего момента
Расчет изгибающего момента и силы сдвига для свободно опертой балки

Калькулятор момента инерции
Рассчитать момент инерции плоских секций, например. швеллер, угол, тройник и т. д.

Калькулятор железобетона
Расчет прочности железобетонной балки

Калькулятор распределения моментов
Решение неопределенных балок

Калькулятор прогиба и уклона
Расчет прогиба и уклона свободно опертой балки для многих случаев нагрузки Калькулятор фиксированной балки
Инструмент для расчета изгибающего момента и поперечной силы для фиксированной балки для многих вариантов нагрузки

Калькулятор BM и SF для кантилевера
Расчет SF и BM для кантилевера

Калькулятор прогиба и уклона для кантилевера
Для многих вариантов нагружения консоли

Калькулятор нависающей балки
Для расчета SF и BM для многих вариантов нагружения для свисающей балки

7 Подробнее Ссылки

Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства

Научные статьи
Научные работы, диссертации и диссертации

Небоскребы мира
Содержащие высотные здания по всему миру

Предстоящие конференции
Перечень конференций, семинаров и практикумов по гражданскому строительству

Профиль инженеров-строителей
Узнайте о выдающихся инженерах-строителях

Профессиональные общества
Профессиональные общества инженеров-строителей
Во всем мире 0

Продолжайте посещать для получения обновлений или присоединяйтесь к нашему списку рассылки, чтобы получать обновления

Ищите на нашем веб-сайте для получения дополнительной информации.