Метод ферма – Метод факторизации Ферма — Википедия. Что такое Метод факторизации Ферма

Факторизация целых чисел — Википедия

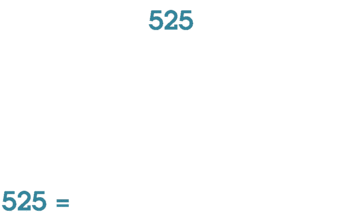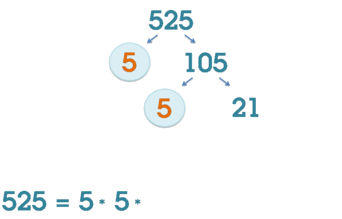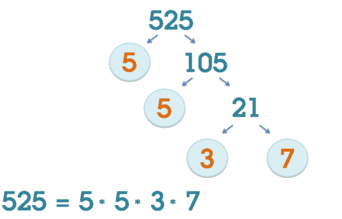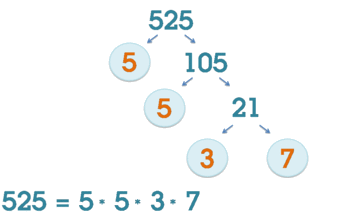Схематическая иллюстрация факторизации числа 525.

Факториза́цией натурального числа называется его разложение в произведение простых множителей. Существование и единственность (с точностью до порядка следования множителей) такого разложения следует из основной теоремы арифметики.

В отличие от задачи распознавания простоты числа, факторизация предположительно является вычислительно сложной задачей. В настоящее время неизвестно, существует ли эффективный не квантовый алгоритм факторизации целых чисел. Однако доказательства того, что не существует решения этой задачи за полиномиальное время, также нет.

Предположение о том, что для больших чисел задача факторизации является вычислительно сложной, лежит в основе широко используемых алгоритмов (например, RSA). Множество областей математики и информатики находят применение в решении этой задачи. Среди них: эллиптические кривые, алгебраическая теория чисел и квантовые вычисления.

Задача поиска эффективных способов разложения целых чисел на множители интересовала математиков с давних времён, особенно специалистов в области теории чисел. Существуют предположения о том, что Ферма был одним из первых, кто предложил метод разложения, заключающийся в том, чтобы представить число в виде разности квадратов n=x2−y2{\displaystyle n=x^{2}-y^{2}}, а затем, вычисляя gcd(n,x−y){\displaystyle \gcd(n,x-y)}, попытаться найти нетривиальный делитель n{\displaystyle n}. Данный способ позволяет находить два мало отличающихся по величине делителя числа быстрее, чем простой перебор делителей^[1].

Создание алгоритма RSA стимулировало бурные исследования в области факторизации целых чисел.

Далее Лежандр обнаружил, что при таком подходе достаточно получить сравнение x2≡y2modn{\displaystyle x^{2}\equiv y^{2}\mod n}, и использовал для этого цепные дроби. Также Эйлером и Гауссом были предложены некоторые способы нахождения чисел, связанных этим сравнением^[1].

Одним из ключевых моментов в развитии факторизации целых чисел было создание алгоритма RSA, что возобновило интерес учёных в данном направлении, так как имело практическое применение в области шифрования. Этот алгоритм был предложен в 1977 году тремя учёными Рональдом Ривестом, Ади Шамиром и Леонардом Адлеманом из Массачусетского Технологического Института и назван по первым буквам фамилий авторов методом RSA. Он основан на идее криптографии с открытым ключом и для взлома системы необходимо выполнить разложение числа на простые сомножители. На момент публикации алгоритма RSA были известны методы, которые позволяли факторизовать числа, состоящие не более чем из 25—30 цифр, а наиболее известным и применяемым все ещё оставался метод Ферма. Метод RSA позволяет факторизовывать числа из 100 и более десятичных знаков. Создатели, в свою очередь, пообещали за факторизацию числа из 129 десятичных знаков символические сто долларов США^[2].

На популярность задачи факторизации также повлияла публикация в 1977 году в журнале Scientific American Мартина Гарднера «Новый алгоритм шифрования, для взлома которого потребуются миллионы лет».^[3] Столь громкое название было воспринято в качестве вызова всему математическому сообществу. В результате этой гонки было предложено несколько новых и нестандартных идей факторизации^[2].

Эпопея с разложением 129-значного числа завершилась в 1994 году, когда коллектив под руководством А. Ленстры, используя 1600 компьютеров, подготовил за 220 дней систему линейных уравнений, содержавшую более полумиллиона неизвестных. Решение этой системы суперкомпьютером заняло два дня. Несмотря на то, что в то время уже были известны методы решета числового поля, данный результат был получен с помощью алгоритма квадратичного решета^[2].

Как правило, на вход таких алгоритмов подаётся число n∈N{\displaystyle n\in \mathbb {N} }, которое необходимо факторизовать, состоящее из N=[log2⁡n]+1{\displaystyle N=[\log _{2}n]+1} символов (если n{\displaystyle n} представлено в двоичном виде)^[4]. При этом алгоритм ищет первый простой делитель, после чего, при необходимости, можно запустить алгоритм заново для дальнейшей факторизации. Также, прежде чем начинать факторизацию большого числа, следует убедиться в том, что оно не простое. Для этого достаточно пройти тест числа на простоту. Эта задача детерминированно разрешима за полиномиальное время^[5].

В зависимости от сложности алгоритмы факторизации можно разбить на две группы. Первая группа — экспоненциальные алгоритмы, сложность которых экспоненциально зависит от длины входящих параметров (то есть от длины N{\displaystyle N} самого числа в бинарном представлении). Вторая группа — субэкспоненциальные алгоритмы.

Вопрос о существовании алгоритма факторизации с полиномиальной сложностью на классическом компьютере является одной из важных открытых проблем современной теории чисел. В то же время факторизация с полиномиальной сложностью возможна на квантовом компьютере с помощью алгоритма Шора (класс BQP)^[6].

Экспоненциальные алгоритмы[править | править код]

Перебор возможных делителей[править | править код]

Сложность O(nlog2⁡n){\displaystyle O({\sqrt {n}}\log ^{2}n)} или O(nlog⁡n){\displaystyle O({\sqrt {n}}\log n)}.

Один из самых простых и очевидных алгоритмов факторизации, заключающийся в том, чтобы последовательно делить факторизуемое число n{\displaystyle n} на натуральные числа от 1{\displaystyle 1} до ⌊n⌋{\displaystyle \lfloor {\sqrt {n}}\rfloor }. Формально достаточно делить только на простые числа в этом интервале, однако, для этого необходимо знать их множество. На практике составляется таблица простых чисел и производится проверка небольших чисел (например, до 216{\displaystyle 2^{16}}). Для очень больших чисел алгоритм не используется в силу низкой скорости работы^[7].

Пример алгоритма^[8]

Шаг 1. Начальная установка. Присвоить t=0,k=0,n=N{\displaystyle t=0,k=0,n=N}(В ходе выполнения алгоритма переменные t,k,n{\displaystyle t,k,n} подчинены следующим условиям: n=N/p1…pt{\displaystyle n=N/p_{1}…p_{t}} и n{\displaystyle n} не имеет простых множителей, меньших dk{\displaystyle d_{k}})

Шаг 2. n=1?{\displaystyle n=1?} Если n=1{\displaystyle n=1}, алгоритм заканчивается.

Шаг 3. Разделить. Присвоить q=⌊n/dk⌋,r=nmoddk.{\displaystyle q=\lfloor n/d_{k}\rfloor ,r=n\mod d_{k}.} (Здесь q{\displaystyle q} и r{\displaystyle r} соответственно частное и остаток от деления числа n{\displaystyle n} на dk{\displaystyle d_{k}}.)

Шаг 4. Остаток равен нулю? Если r≠0{\displaystyle r\neq 0}, то перейти к шагу 6.

Шаг 5. Множитель найден. Увеличить t{\displaystyle t} на 1{\displaystyle 1} и присвоить pt=dk,n=q{\displaystyle p_{t}=d_{k},n=q}. Возвратиться к шагу 2.

Шаг 6. Частное мало? Если q>dk{\displaystyle q>d_{k}}, увеличить k{\displaystyle k} на 1 и возвратиться к шагу 3.

Шаг 7. n — простое число. Увеличить t{\displaystyle t} на 1{\displaystyle 1}, присвоить pt=n{\displaystyle p_{t}=n} и завершить выполнение алгоритма.

Метод факторизации Ферма[править | править код]

Сложность O(n){\displaystyle O(n)} или O(exp(N)){\displaystyle O(exp(N))}.

Идея алгоритма заключается в поиске таких чисел A{\displaystyle A} и B{\displaystyle B}, что факторизуемое число n представимо в виде: n=A2−B2=(A−B)(A+B){\displaystyle n=A^{2}-B^{2}=(A-B)(A+B)}. Как и метод пробного деления, обычно не применяется на практике для факторизации больших чисел, так как имеет экспоненциальную сложность. Метод примечателен тем, что реализуем без операции деления, а только лишь с операциями сложения и вычитания^[9]. Следует так же отметить, что если n=pq{\displaystyle n=pq}, при условии того, что p{\displaystyle p} и q{\displaystyle q} — простые числа не сильно отличающиеся по величине, то метод Ферма факторизует n достаточно быстро^[10].

Пример модификации алгоритма^[11]

Шаг 1. Начальная установка. Присвоить x=2⌊N⌋+1,y=1,r=⌊N⌋2−N.{\displaystyle x=2\lfloor {\sqrt {N}}\rfloor +1,y=1,r=\lfloor {\sqrt {N}}\rfloor ^{2}-N.} (Во время выполнения этого алгоритма величины x, y, r отвечают соответственно величинам 2x+1,2y+1,x2−y2−N{\displaystyle 2x+1,2y+1,x^{2}-y^{2}-N} в уравнении N=uv=x2−y2(x=u+v2,y=u−v2){\displaystyle N=uv=x^{2}-y^{2}(x={\dfrac {u+v}{2}},y={\dfrac {u-v}{2}})}. Должно соблюдаться условие |r|<x,y<x{\displaystyle |r|<x,y<x}.)

Шаг 2. Выполнено? Если r=0{\displaystyle r=0}, то выполнение алгоритма завершается. Имеем

N=x−y2⋅x+y−22{\displaystyle N={\frac {x-y}{2}}\cdot {\frac {x+y-2}{2}}}

Шаг 3. Шаг по x. Присвоить r=r+x{\displaystyle r=r+x} и x=x+2{\displaystyle x=x+2}.

Шаг 4. Шаг по y. Присвоить r=r−y{\displaystyle r=r-y} и y=y+2{\displaystyle y=y+2}.

Шаг 5. Проверить r. Если r>0{\displaystyle r>0}, то возвратиться к шагу 4, иначе возвратиться к шагу 2.

ρ-алгоритм Полларда[править | править код]

Сложность O(n1/4){\displaystyle O(n^{1/4})}.

Алгоритм Полларда является вероятностным алгоритмом, позволяющим находить делитель составного числа n{\displaystyle n}, работающим со сложностью, зависящей лишь от величины делителя, но не величины факторизуемого числа n{\displaystyle n}. Это обуславливает удобство применимости данного алгоритма в тех случаях, когда другие алгоритмы, сложность которых зависит от n{\displaystyle n}, становятся неэффективны^[12]. Примечателен так же тем, что существует вариант реализации такого алгоритма, при котором достаточно в памяти хранить всего 3 целых числа^[13].

Пример алгоритма^[14]

Шаг 1. Выбираем небольшое число x0{\displaystyle x_{0}} и строим последовательность чисел xk,k=0,1,2,…,{\displaystyle {x_{k}},k=0,1,2,…,} определяя каждое следующее xk+1{\displaystyle x_{k+1}} по формуле: xk+1=xk2−1modn{\displaystyle x_{k+1}=x_{k}^{2}-1\mod n}

Шаг 2. Одновременно на каждом шаге i{\displaystyle i} вычисляем Н.О.Д d{\displaystyle d} числа n{\displaystyle n} и всевозможных разностей |xi−xj|{\displaystyle |x_{i}-x_{j}|}, где j<i{\displaystyle j<i}.

Шаг 3. Когда будет найден d=gcd(n,|xi−xj|){\displaystyle d=\gcd(n,|x_{i}-x_{j}|)}, отличный от 1{\displaystyle 1}, вычисление заканчивается. Найденное d{\displaystyle d} является делителем n{\displaystyle n}. Если n/d{\displaystyle n/d} не является простым числом, то процедуру можно продолжить, взяв вместо n{\displaystyle n} число n/d{\displaystyle n/d}.

Алгоритм Ленстры[править | править код]

Сложность O(n1/3log2⁡n){\displaystyle O(n^{1/3}\log ^{2}n)}.

Следует отметить, что несмотря на относительно неплохую эффективность среди экспоненциальных алгоритмов, в алгоритме Ленстры есть необходимость неоднократно вычислять квадратный корень в одном из шагов алгоритма, что, безусловно, является более трудоёмким, чем сложение или вычитание^[15].

Пример модификации алгоритма^[16]

Пусть r,s,n{\displaystyle r,s,n} — натуральные числа, удовлетворяющие условиям 1≤r<s<n;n1/3<s;gcd(r,s)=1{\displaystyle 1\leq r<s<n;\;n^{1/3}<s;\;\gcd(r,s)=1}

Шаг 1. С помощью обобщённого алгоритма Евклида найти r∗∈N,rr∗≡1mods{\displaystyle r^{*}\in \mathbb {N} ,rr^{*}\equiv 1\mod s}. Найти r′{\displaystyle r’} такое, что r′≡r∗nmods,0≤r′<s{\displaystyle r’\equiv r^{*}n\mod s,0\leq r'<s}.

Шаг 2. Для очередного значения i=0,1,2,…{\displaystyle i=0,1,2,…} найти числа ai,bi,ci{\displaystyle a_{i},b_{i},c_{i}} по следующим правилам:

a0=s,b0=0,c0=0{\displaystyle a_{0}=s,\;b_{0}=0,\;c_{0}=0} a1=rr′mods,0<a1≤s,b1=1,c1≡n−rr′sr∗(mods){\displaystyle a_{1}=rr’\mod s,0<a_{1}\leq s,\;b_{1}=1,\;c_{1}\equiv {\frac {n-rr’}{s}}r^{*}(\mod s)}

при i≥2{\displaystyle i\geq 2}:

ai=ai−2−qiai−1,bi=bi−2−qibi−1,ci=ci−2−qici−1(mods){\displaystyle a_{i}=a_{i-2}-q_{i}a_{i-1},\;\;b_{i}=b_{i-2}-q_{i}b_{i-1},\;\;c_{i}=c_{i-2}-q_{i}c_{i-1}(\mod s)}

qi{\displaystyle q_{i}} — частное от деления ai−2{\displaystyle a_{i-2}} на ai−1{\displaystyle a_{i-1}}, за исключением случая, когда i{\displaystyle i} нечётно и остаток от деления равен нулю.

Шаг 3. Для очередного выбора ai,bi,ci{\displaystyle a_{i},b_{i},c_{i}} найти все целые числа c{\displaystyle c}, удовлетворяющие условиям

c=cimods{\displaystyle c=c_{i}\mod s},

|c|<s,{\displaystyle |c|<s,\;\;\;\;\;\;} если i{\displaystyle i} четное,

2aibi≤c≤ns2+aibi,{\displaystyle 2a_{i}b_{i}\leq c\leq {\frac {n}{s^{2}}}+a_{i}b_{i},\;\;} если i{\displaystyle i} нечетное.

Шаг 4. Для каждого c из шага 3 решить в целых числах систему уравнений

{xai+ybi=c(xs+r)(ys+r′)=n{\displaystyle \left\{{\begin{array}{rcl}xa_{i}+yb_{i}\;\;\;\;\;\;&=&c\\(xs+r)(ys+r’)&=&n\\\end{array}}\right.}

Если x{\displaystyle x} и y{\displaystyle y} окажутся неотрицательными целыми числами, то добавить xs+r{\displaystyle xs+r}

Шаг 5. Если ai=0{\displaystyle a_{i}=0}, то алгоритм заканчивает работу. Иначе, возвращаемся на шаг 2 к следующему значению i{\displaystyle i}.

Алгоритм Полларда — Штрассена[править | править код]

Сложность O(n1/4log4

Метод факторизации Ферма — Национальная библиотека им. Н. Э. Баумана

Материал из Национальной библиотеки им. Н. Э. Баумана
Последнее изменение этой страницы: 14:56, 14 мая 2016.

Метод факторизации Ферма

Пусть n=p⋅q{\displaystyle n = p \cdot q } – известное целое число, являющееся произведением двух неизвестных простых чисел p{\displaystyle p} и q{\displaystyle q }, которые требуется найти. Большинство современных методов факторизации основано на идее, предложенной еще Пьером Ферма, заключающейся в поиске пар натуральных чисел A{\displaystyle A} и B{\displaystyle B } таких, что выполняется соотношение:

n=A2−B2=(A−B)(A+B){\displaystyle n = A^2 — B^2 = (A-B)(A+B)}

Алгоритм 1

1. Вычислим целую часть от квадратного корня из n{\displaystyle n}: m=⌊n⌋{\displaystyle m = \left \lfloor \sqrt{n} \right \rfloor }
2. Для x=1,2,…{\displaystyle x = 1,2,\dots } будем вычислять значения q(x)=(m+x)2−n{\displaystyle q(x)=(m+x)^2-n } до тех пор, пока q(x){\displaystyle q(x) } не окажется равным полному квадрату.
3. Пусть q(x){\displaystyle q(x)} является полным квадратом, например, числа B{\displaystyle B }:q(x)=B2{\displaystyle q(x) = B^2 }. Определим A=m+x{\displaystyle A=m+x }, откуда из равенства A2−n=B2{\displaystyle A^2 -n = B^2 } найдем n=A2−B2=(A+B)(A−B){\displaystyle n =A^2-B^2 = (A+B)(A-B) }, и искомые делители p{\displaystyle p} и q{\displaystyle q} вычисляются как p=A+B{\displaystyle p=A+B}, q=A−B{\displaystyle q=A-B}.

Пример

Пусть n=19691{\displaystyle n=19691}. Вычислим m=⌊n⌋=140{\displaystyle m = \left \lfloor \sqrt{n} \right \rfloor = 140 }.

x{\displaystyle x}	y{\displaystyle y}	y{\displaystyle \sqrt{y}}
1	190	13,78
2	473	21.75
3	758	27.53
4	1045	32.33
5	1334	36,52
6	1625	40,31
7	1918	43,79
8	2213	47,04
9	2510	50,10
10	2809	53

Из последнего столбца получим: (140+10)2−n=532{\displaystyle (140+10)^2-n=532}, откуда n=1502−532=203⋅97,19691=203⋅97{\displaystyle n=1502-532=203 \cdot 97, \, 19691=203 \cdot 97}

Улучшение алгоритма

Метод факторизации Ферма можно значительно улучшить. Для этого необходимо получить сравнение вида t2≡s2(modn){\displaystyle t^2 \equiv s^2 (mod \, n) } с t≢±s(modn){\displaystyle t \not\equiv \pm s (mod \, n) }. В этом случае можно сразу найти множитель числа n{\displaystyle n}, вычисляя НОД (t±s,n){\displaystyle (t \pm s,\, n)}. Действительно, n{\displaystyle n} делит t2−s2=(t+s)(t−s){\displaystyle t^2 — s^2 = (t+s)(t-s)}, но не делит ни t+s{\displaystyle t+s}, ни t−s{\displaystyle t-s}. Тогда НОД (t+s,n){\displaystyle (t+s, \, n)} должен быть собственным делителем a{\displaystyle a} числа n{\displaystyle n}, и тогда b=na{\displaystyle b=\frac{n}{a}} делит НОД (t−s,n){\displaystyle (t-s, \, n)}.

Под понятием «наименьший абсолютный вычет» числа a{\displaystyle a} по модулю n{\displaystyle n} будем понимать целое число в интервале (−n/2,n/2){\displaystyle (-n/2, \, n/2)}, сравнимое с a{\displaystyle a}.

Определение «Факторная база»

Факторной базой[1] называется множество B={p1,p2,…,ph}{\displaystyle B=\{p_{1},p_{2},…,p_{h}\}\,\!}, где p1{\displaystyle p_{1}\,\!}-либо простое, либо (−1){\displaystyle (-1)}, остальные числа — простые. Будем говорить, что квадрат числа b{\displaystyle b} есть B{\displaystyle B}-число, если наименьший абсолютный вычет b2(modn){\displaystyle b^2 (mod \, n) } можно записать как произведение чисел из B{\displaystyle B}.

Пример

Пусть n=4633{\displaystyle n=4633 } и B={−1,2,3}{\displaystyle B=\{-1,2,3\}\,\!}. Тогда квадраты чисел 67, 68, 69 являются B{\displaystyle B}-числами.

672=4489=−144=−1⋅24⋅32(mod4633)632=4624=−9=−1⋅32(mod4633)692=128=27(mod4633){\displaystyle \begin{align} &67^2=4489=-144=-1\cdot 2^4\cdot 3^2 \, (mod \, 4633)\\ &63^2=4624=-9=-1\cdot 3^2 \, (mod \, 4633) \\ &69^2=128=2^7\, (mod \, 4633) \end{align} \,\!}

Рассмотрим векторное пространство F2h{\displaystyle F^h_2}, где h=|B|{\displaystyle h=|B|}. Сопоставим каждому B{\displaystyle B}-числу вектор ϵ¯∈F2h{\displaystyle \bar\epsilon \in F^h_2}. Запишем b2(modn){\displaystyle b^2 (mod \, n)} в виде ∏j=1hpjαj,ϵj=αj(modn){\displaystyle \prod_{j=1}^h{p_{j}^{{\alpha}_j}} , \, \epsilon_j = \alpha_j (mod \, n)}. Тогда числу 67{\displaystyle 67} соответствует вектор (1,0,0){\displaystyle (1, \, 0, \, 0)}, 68−(1,0,0),69−(0,1,0){\displaystyle 68 \, — \, (1, \, 0, \, 0), \, 69 \, — \, (0, \, 1, \, 0)}.

Пусть у нас есть такое множество B{\displaystyle B}-чисел, что сумма соотвествующих векторов ϵ¯{\displaystyle \bar\epsilon} есть нулевой вектор. Тогда произведение наименьших абсолютных вычетов bi2{\displaystyle b_i^2} равно произведению четных степеней всех pj inB{\displaystyle p_j \ in B}, следовательно, ∏ai=∏j=1hpj∑iαij{\displaystyle \prod{a_i} \, = \, \prod_{j=1}^{h}{p_j^{\sum_i{\alpha_{ij}}}} }. Показатель каждого pj{\displaystyle p_{j}} — четное число. Тогда правая часть равенства есть квадрат числа ∏jpjγj{\displaystyle \prod_j{p_j^{\gamma_j}}}, где γj=12∑iαij{\displaystyle \gamma_j \, = \, \frac{1}{2} \sum_i{\alpha_{ij}}}. Таким образом получили, что b=∏ibi(modn){\displaystyle b \, = \, \prod_i{b_i} \, (mod \, n) } и c=∏jpjγj(modn){\displaystyle c \, = \, \prod_j{p_j^{\gamma_j}} \, (mod \, n)} имеют равные квадраты.В случае b≡±c(modn){\displaystyle b \, \equiv \, \pm c \, (mod \, n)} необходимо выбрать другую факторную базу и продолжить.

Таким образом, b=67⋅68≡−77(mod4633){\displaystyle b \, = \, 67 \cdot 68 \equiv -77 \, (mod \, 4633) } и c=2γ23γ3=36{\displaystyle c \, = \, 2^{\gamma_2}3^{\gamma_3} \, = \, 36}. Так как −7≢±36(mod4633){\displaystyle -7 \not\equiv \pm 36 \, (mod \, 4633)}, то делитель равен НОД (−77+36,4633)=41{\displaystyle (-77+36, \, 4633) \, = \, 41}. Получаем, что n=41⋅113{\displaystyle n \, = \, 41 \cdot 113 }.

Примечания

1. ↑ ‘Коблиц Н, Курс теории чисел и криптографии. — М. : ТВП, 2001. — С. 254.

Метод факторизации Ферма — Вики

Метод факторизации Ферма — алгоритм факторизации (разложения на множители) нечётного целого числа n{\displaystyle n}, предложенный Пьером Ферма (1601—1665) в 1643 году.

Метод основан на поиске таких целых чисел x{\displaystyle x} и y{\displaystyle y}, которые удовлетворяют соотношению x2−y2=n{\displaystyle x^{2}-y^{2}=n}, что ведёт к разложению n=(x−y)⋅(x+y){\displaystyle n=(x-y)\cdot (x+y)}.

История

В начале XVII века во Франции математические идеи начали активно распространяться между учёными посредством переписки. В 1638 году к кругу переписывающихся учёных присоединился Пьер Ферма. Переписка была удобным способом общения, так как Ферма жил в Тулузе, а многие его знакомые учёные жили в Париже. Одним из таких учёных был Марен Мерсенн, занимавшийся распространением писем, пересылкой и связью многих учёных между собой. 26 декабря 1638 года в письме Мерсенну Ферма упомянул, что нашёл метод, с помощью которого можно находить делители положительных чисел, но какие-либо подробности и описание метода он опустил. На тот момент Мерсенн также вёл переписку с французским математиком Бернаром Френиклем де Бесси, занимавшимся, как и Ферма, теорией чисел, в частности, делителями натуральных чисел и совершенными числами. В начале 1640 года, узнав о том, что Ферма получил метод нахождения делителей, Френикль пишет Мерсенну, и тот пересылает письмо Ферма. Мерсенн долгое время был связующим звеном между двумя математиками в их переписке. Именно в письмах Френиклю Ферма смог доказать корректность метода факторизации, а также впервые сформулировать и обосновать основные положения теоремы, которая позже была названа Малой теоремой Ферма ^[1][2].

Обоснование

Метод Ферма основан на теореме о представлении числа в виде разности двух квадратов:

Если n>1{\displaystyle n>1} нечетно, то существует взаимно однозначное соответствие между разложением на множители n=a⋅b{\displaystyle n=a\cdot b} и представлением в виде разности квадратов n=x2−y2{\displaystyle n=x^{2}-y^{2}} с x>y>0{\displaystyle x>y>0}, задаваемое формулами x=a+b2

Метод факторизации Ферма Википедия

Метод факторизации Ферма — алгоритм факторизации (разложения на множители) нечётного целого числа n{\displaystyle n}, предложенный Пьером Ферма (1601—1665) в 1643 году.

Метод основан на поиске таких целых чисел x{\displaystyle x} и y{\displaystyle y}, которые удовлетворяют соотношению x2−y2=n{\displaystyle x^{2}-y^{2}=n}, что ведёт к разложению n=(x−y)⋅(x+y){\displaystyle n=(x-y)\cdot (x+y)}.

История

В начале XVII века во Франции математические идеи начали активно распространяться между учёными посредством переписки. В 1638 году к кругу переписывающихся учёных присоединился Пьер Ферма. Переписка была удобным способом общения, так как Ферма жил в Тулузе, а многие его знакомые учёные жили в Париже. Одним из таких учёных был Марен Мерсенн, занимавшийся распространением писем, пересылкой и связью многих учёных между собой. 26 декабря 1638 года в письме Мерсенну Ферма упомянул, что нашёл метод, с помощью которого можно находить делители положительных чисел, но какие-либо подробности и описание метода он опустил. На тот момент Мерсенн также вёл переписку с французским математиком Бернаром Френиклем де Бесси, занимавшимся, как и Ферма, теорией чисел, в частности, делителями натуральных чисел и совершенными числами. В начале 1640 года, узнав о том, что Ферма получил метод нахождения делителей, Френикль пишет Мерсенну, и тот пересылает письмо Ферма. Мерсенн долгое время был связующим звеном между двумя математиками в их переписке. Именно в письмах Френиклю Ферма смог доказать корректность метода факторизации, а также впервые сформулировать и обосновать основные положения теоремы, которая позже была названа Малой теоремой Ферма ^[1][2].

Обоснование

Метод Ферма основан на теореме о представлении числа в виде разности двух квадратов:

Если n>1{\displaystyle n>1} нечетно, то существует взаимно однозначное соответствие между разложением на множители n=a⋅b{\displaystyle n=a\cdot b} и представлением в виде разности квадратов n=x2−y2{\displaystyle n=x^{2}-y^{2}}

Метод факторизации Ферма Википедия

Метод факторизации Ферма — алгоритм факторизации (разложения на множители) нечётного целого числа n{\displaystyle n}, предложенный Пьером Ферма (1601—1665) в 1643 году.

Метод основан на поиске таких целых чисел x{\displaystyle x} и y{\displaystyle y}, которые удовлетворяют соотношению x2−y2=n{\displaystyle x^{2}-y^{2}=n}, что ведёт к разложению n=(x−y)⋅(x+y){\displaystyle n=(x-y)\cdot (x+y)}.

История

В начале XVII века во Франции математические идеи начали активно распространяться между учёными посредством переписки. В 1638 году к кругу переписывающихся учёных присоединился Пьер Ферма. Переписка была удобным способом общения, так как Ферма жил в Тулузе, а многие его знакомые учёные жили в Париже. Одним из таких учёных был Марен Мерсенн, занимавшийся распространением писем, пересылкой и связью многих учёных между собой. 26 декабря 1638 года в письме Мерсенну Ферма упомянул, что нашёл метод, с помощью которого можно находить делители положительных чисел, но какие-либо подробности и описание метода он опустил. На тот момент Мерсенн также вёл переписку с французским математиком Бернаром Френиклем де Бесси, занимавшимся, как и Ферма, теорией чисел, в частности, делителями натуральных чисел и совершенными числами. В начале 1640 года, узнав о том, что Ферма получил метод нахождения делителей, Френикль пишет Мерсенну, и тот пересылает письмо Ферма. Мерсенн долгое время был связующим звеном между двумя математиками в их переписке. Именно в письмах Френиклю Ферма смог доказать корректность метода факторизации, а также впервые сформулировать и обосновать основные положения теоремы, которая позже была названа Малой теоремой Ферма ^[1][2].

Обоснование

Метод Ферма основан на теореме о представлении числа в виде разности двух квадратов:

Если n>1{\displaystyle n>1} нечетно, то существует взаимно однозначное соответствие между разложением на множители n=

Метод факторизації Ферма — Вікіпедія

Метод факторизації Ферма — алгоритм факторизації (розклад на множники) непарного цілого числа n, представлений П’єром Ферма (1601—1665) у 1643 році.

Метод заснований на пошуку таких цілих чисел x{\displaystyle x} і y{\displaystyle y}, які задовольняють відношення x2−y2=n{\displaystyle x^{2}-y^{2}=n}, що веде до розкладу n=(x−y)⋅(x+y){\displaystyle n=(x-y)\cdot (x+y)}.

На початку XVII століття у Франції математичні ідеї почали активно поширюватися між вченими за допомогою листування. В 1638 році до кола вчених, які листувалися приєднався П’єр Ферма. Листування було зручним способом спілкування, так як Ферма жив в Тулузі, а багато його знайомих вчених жили в Парижі.

Одним таким вченим був Марен Мерсенн, який займався розповсюдженням листів, пересиланням і зв’язком багатьох вчених між собою. 26 грудня 1638 року в листі Мерсенну Ферма згадав, що знайшов метод, за допомогою якого можна знаходити подільники позитивних чисел, але будь-які подробиці і опис методу він опустив. На той момент Мерсенн також вів листування з французьким математиком Бернаром Френіклєм де Бессі, який займався, як і Ферма, теорією чисел, зокрема, дільниками натуральних чисел і досконалими числами. На початку 1640 року, дізнавшись про те, що Ферма отримав метод знаходження дільників, Френікль пише Мерсенну, і той пересилає лист Ферма.

Мерсенн довгий час був сполучною ланкою між двома математиками в їх листуванні. Саме в листах Френіклю Ферма зміг довести коректність методу факторизації, а також вперше сформулювати і обґрунтувати основні положення теореми, яка пізніше була названа Малою теоремою Ферма.

Метод Ферма заснований на теоремі про подання числа у вигляді різниці двох квадратів :

Доведення  

Якщо задана факторизація n=a⋅b{\displaystyle n=a\cdot b}, тоді має місце відношення: n=a⋅b=(a+b2)2−(a−b2)2{\displaystyle n=a\cdot b=({\tfrac {a+b}{2}})^{2}-({\tfrac {a-b}{2}})^{2}}. Таким чином виходить уявлення у вигляді різниці двох квадратів. Назад, якщо дано, що n=x2−y2{\displaystyle n=x^{2}-y^{2}}, то праву частину можна розкласти на множники: (x−y)(x+y){\displaystyle (x-y)(x+y)}.

Для розкладання на множники непарного числа n{\displaystyle n} шукається пара чисел (x,y){\displaystyle (x,y)} таких, що x2−y2=n{\displaystyle x^{2}-y^{2}=n}, або (x−y)⋅(x+y)=n{\displaystyle (x-y)\cdot (x+y)=n}. При цьому числа (x+y){\displaystyle (x+y)} і (x−y){\displaystyle (x-y)} є множниками n{\displaystyle n}, можливо, тривіальними (тобто одне з них дорівнює 1, а інше — n{\displaystyle n}.)

У нетривіальною випадку, рівність x2−y2=n{\displaystyle x^{2}-y^{2}=n} рівносильно x2−n=y2{\displaystyle x^{2}-n=y^{2}}, тобто того, що x2−n{\displaystyle x^{2}-n} є квадратом.

Пошук квадрата такого виду починається з x=⌈n⌉{\displaystyle x=\left\lceil {\sqrt {n}}\right\rceil } — найменшого числа, при якому різниця x2−n{\displaystyle x^{2}-n} невід’ємна.

Для кожного значення k∈N,{\displaystyle k\in \mathbb {N} ,} починаючи з k=1{\displaystyle k=1}, обчислюють (⌈n⌉+k)2−n{\displaystyle (\left\lceil {\sqrt {n}}\right\rceil +k)^{2}-n} і перевіряють, чи не є це число точним квадратом. Якщо не є, то k{\displaystyle k} збільшують на одиницю і переходять на наступну ітерацію.

Якщо (⌈n⌉+k)2−n{\displaystyle (\left\lceil {\sqrt {n}}\right\rceil +k)^{2}-n} є точним квадратом, тобто x2−n=(⌈n⌉+k)2−n=y2,{\displaystyle x^{2}-n=(\left\lceil {\sqrt {n}}\right\rceil +k)^{2}-n=y^{2},} то отримано розкладання:

n=x2−y2=(x+y)(x−y)=a⋅b,{\displaystyle n=x^{2}-y^{2}=(x+y)(x-y)=a\cdot b,} в якому x=(⌈n⌉+k){\displaystyle x=(\left\lceil {\sqrt {n}}\right\rceil +k)}

Якщо воно є тривіальним і єдиним, то n{\displaystyle n} — просте.

На практиці значення виразу на (k+1){\displaystyle (k+1)}-ому кроці вираховується з врахуванням значення на k{\displaystyle k}-ому кроці:

(s+1)2−n=s2+2s+1−n,{\displaystyle \left(s+1\right)^{2}-n=s^{2}+2s+1-n,} де s=⌈n⌉+k.{\displaystyle s=\left\lceil {\sqrt {n}}\right\rceil +k.}

Приклад з малим числом ітерацій[ред. | ред. код]

Візьмемо число n=10873{\displaystyle n=10873}. Обчислимо s=⌈n⌉=105.{\displaystyle s=\left\lceil {\sqrt {n}}\right\rceil =105.} Для k=1,2,…{\displaystyle k=1,2,…} будемо обчислювати значення функції s+k{\displaystyle s+k}. Для подальшої простоти побудуємо таблицю, яка буде містити значення y=(s+k)2−n{\displaystyle y=(s+k)^{2}-n} і y{\displaystyle {\sqrt {y}}} на кожному кроці ітерації. отримаємо:

k{\displaystyle k}	y{\displaystyle y}	y{\displaystyle {\sqrt {y}}}
1	363	19,052
2	576	24

Як видно з таблиці, вже на другому кроці ітерації було отримано ціле значення y{\displaystyle {\sqrt {y}}}.

Таким чином має місце такий вираз: (105+2)2−n=242{\displaystyle (105+2)^{2}-n=24^{2}}. Звідси випливає, що n=1072−242=131⋅83=10873.{\displaystyle n=107^{2}-24^{2}=131\cdot 83=10873.}

Приклад з великим числом ітерацій[ред. | ред. код]

<! — Приклад не дуже добрий: відразу видно, що 89755 ділиться на 5. Добре б навести приклад без малих дільників -> Нехай n=89755.{\displaystyle n=89755.} Тоді n≈299,591{\displaystyle {\sqrt {n}}\approx 299,591} або s=⌈n⌉=300.{\displaystyle s=\left\lceil {\sqrt {n}}\right\rceil =300.}

k{\displaystyle k}	y{\displaystyle y}	y{\displaystyle {\sqrt {y}}}
77	52374	228,854
78	53129	230,497
79	53886	232,134
80	54645	233,763
81	55406	235,385
82	56169	237

y=237{\displaystyle {\sqrt {y}}=237}

a=s+k+y=300+82+237=619{\displaystyle a=s+k+{\sqrt {y}}=300+82+237=619}

b=s+k−y=300+82−237=145{\displaystyle b=s+k-{\sqrt {y}}=300+82-237=145}

Даний розклад не є кінцевим, оскільки, очевидно, що число 145{\displaystyle 145} не є простим: 145=29⋅5.{\displaystyle 145=29\cdot 5.}

У підсумку, кінцевий розклад вихідного числа n{\displaystyle n} на результат простих множників 89755=5⋅29⋅619.{\displaystyle 89755=5\cdot 29\cdot 619.}

Оцінка продуктивності[ред. | ред. код]

Найбільша ефективність розрахунку методом факторизації Ферма досягається в разі, коли множники числа n{\displaystyle n} приблизно рівні між собою. Це забезпечує відносно короткий пошук послідовності

s2−n, (s+1)2−n, (s+2)2−n … (s+k)2−n.{\displaystyle s^{2}-n,\ (s+1)^{2}-n,\ (s+2)^{2}-n\ …\ (s+k)^{2}-n.}

У найгіршому варіанті, коли, наприклад, a{\displaystyle a} близько до n{\displaystyle n} а b{\displaystyle b} близько до 1, алгоритм Ферма працює гірше в порівнянні з методом перебору дільників. Число ітерацій для даного випадку:

Iter⁡(n)=a+b2−⌈n1/2⌉≈n2−⌈n1/2⌉,{\displaystyle \operatorname {Iter} (n)={\tfrac {a+b}{2}}-\left\lceil {n}^{1/2}\right\rceil \thickapprox {\tfrac {n}{2}}-\left\lceil {n}^{1/2}\right\rceil ,} тобто, очевидно, що воно має порядок O(n).{\displaystyle O(n).}

Метод факторизації Ферма буде працювати не гірше методу перебору дільників, якщо Iter⁡(n)<n1/2,{\displaystyle \operatorname {Iter} (n)<{n}^{1/2},} звідси можна отримати оцінку для більшого подільника a<4n1/2.{\displaystyle a<4{n}^{1/2}.} Отже, метод Ферма має експонентну оцінку і, як метод пробного поділу, не підходить для розкладання великих чисел. Можна підвищити ефективність, якщо виконати спочатку пробне розподіл числа n{\displaystyle n} на числа від 2 до деякої константи B, а потім виконати пошук подільників методом Ферма. Такий похід допомагає позбутися від малих дільників числа n{\displaystyle n}.

Оптимізація методом перебору дільників[ред. | ред. код]

Припустимо, що ми намагаємося розкласти на множники число n = 2345678917 методом Ферма, але крім b обчислюємо також і a − b. Починаючи з n{\displaystyle {\sqrt {n}}}, можна записати:

a	48 433	48 434	48 435	48 436
b2	76 572	173 439	270 308	367 179
b	276,7	416,5	519,9	605,9
a − b	48 156,3	48 017,5	47 915,1	47 830,1

Якби тепер для розкладання числа n{\displaystyle n} стали використовувати метод перебору дільників, то доцільно було б перевіряти подільники n{\displaystyle n} тільки до 47 830, а не до 48 432, так як якщо б існував дільник більше, то він був би знайдений методом Ферма. Отже, всього за чотири етапи методом Ферма були перевірені всі подільники n{\displaystyle n} від 47 830 до 48 432.

Таким чином, можна комбінувати метод Ферма з методом перебору дільників. Досить вибрати число c>n{\displaystyle c>{\sqrt {n}}} і використовувати метод Ферма для перевірки подільників між c{\displaystyle c} і n{\displaystyle {\sqrt {n}}}, а подільники, що залишилися можна перевірити методом перебору дільників, причому перевіряти подільники потрібно тільки до числа c−c2−n{\displaystyle c-{\sqrt {c^{2}-n}}}.

В наведеному вище прикладі, коли c=48436{\displaystyle c=48436}, подільники необхідно перебирати до числа 47830. Також, наприклад, можна вибрати число c=55000{\displaystyle c=55000}, що дає межу 28937.

Комбінація методів хороша, так як при достатній різниці між дільниками числа n{\displaystyle n} метод перебору дільників ефективніше методу Ферма. Це ілюструє наступний приклад:

a	60 001	60 002
b2	1 254 441 084	1 254 561 087
b	35 418,1	35 419,8
a − b	24 582,9	24 582,2

При пошуку квадрата натурального числа в послідовності чисел a2−n{\displaystyle a^{2}-n} годі й обчислювати квадратний корінь з кожного значення цієї послідовності, і навіть не перевіряти всі можливі значення для a. Для прикладу розглянемо число n=2345678917{\displaystyle n=2345678917}:

a	48 433	48 434	48 435	48 436
b2	76 572	173 439	270 308	367 179
b	276,7	416,5	519,9	605,9

Можна відразу, не обчислюючи квадратного кореня, сказати, що жодне зі значень b2{\displaystyle b^{2}} в таблиці не є квадратом. Досить, наприклад, скористатися тим, що всі квадрати натуральних чисел, взяті по модулю 20, дорівнюють одному з наступних значень: 0, 1, 4, 5, 9, 16. Ці значення повторюються при кожному збільшенні a на 10. У прикладі n=17{\displaystyle n=17} по модулю 20, тому віднімаючи 17 (або додаючи 3), отримуємо, що число b2{\displaystyle b^{2}} по модулю 20 дорівнює одному з наступних: 3, 4, 7, 8, 12, 18. Але так як b{\displaystyle b} — натуральне число, то звідси отримуємо, що b2{\displaystyle b^{2}} по модулю 20 може дорівнювати лише 4. Отже, a2=1{\displaystyle a^{2}=1} по модулю 20 і a=1{\displaystyle a=1} або a=9{\displaystyle a=9} по модулю 10 . Таким чином, можна перевіряти корінь виразу a2−n{\displaystyle a^{2}-n} не для всіх a{\displaystyle a}, а тільки для тих, які закінчуються на 1 або 9.

Аналогічно як модуль можна використовувати будь-які ступені різних простих чисел. Наприклад, взявши той же число n=2345678917{\displaystyle n=2345678917}, знаходимо:

По модулю 16:	Квадрати рівні	0, 1, 4 або 9
	n mod 16 рівне	5
	отже, a2{\displaystyle a^{2}} рівне	9
	і a рівне	3, 5, 11 або 13 по модулю 16
По модулю 9:	Квадрати рівні	0, 1, 4, або 7
	n mod 9 рівне	7
	отже, a2{\displaystyle a^{2}} рівне	7
	і a рівне	4 або 5 по модулю 9

Оптимізація множником[ред. | ред. код]

Метод Ферма добре працює в разі, коли у числа n{\displaystyle n} є множник, приблизно рівний квадратному кореню з n{\displaystyle n}.

Якщо відомо приблизне співвідношення d/c{\displaystyle d/c} між множниками числа n{\displaystyle n}, то можна вибрати раціональне число u/v{\displaystyle u/v}, приблизно рівне цьому співвідношенню. Тоді можна записати наступне рівність: nuv=cv⋅du{\displaystyle nuv=cv\cdot du}, де множники cv{\displaystyle cv} і du{\displaystyle du} близькі в силу зроблених припущень. Тому застосувавши метод Ферма для розкладання числа nuv{\displaystyle nuv}, їх можна швидко знайти. Далі для знаходження c{\displaystyle c} і d{\displaystyle d} можна використовувати рівності gcd(n,cv)=c{\displaystyle \gcd(n,cv)=c} і gcd(n,du)=d{\displaystyle \gcd(n,du)=d} (в разі, якщо u{\displaystyle u} не ділиться на c{\displaystyle c} і v{\displaystyle v} не ділиться на d{\displaystyle d}).

У загальному випадку, коли співвідношення між множниками n{\displaystyle n} невідомо, можна спробувати використовувати різні співвідношення u/v{\displaystyle u/v}, і пробувати розкласти вийшло в результаті число

Ферма, Пьер — Википедия

Пьер де Ферма́ (фр. Pierre de Fermat, 17 августа 1601 (1601-08-17) — 12 января 1665) — французский математик-самоучка, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года — советник парламента в Тулузе. Блестящий полиглот. Наиболее известен формулировкой Великой теоремы Ферма, «самой знаменитой математической загадки всех времён»^[3].

Пьер Ферма родился 17 августа 1601 (1601-08-17) года в гасконском городке Бомон-де-Ломань (Beaumont-de-Lomagne, Франция). Его отец, Доминик Ферма, был зажиточным торговцем-кожевником, вторым городским консулом. В семье, кроме Пьера, были ещё один сын и две дочери. Ферма получил юридическое образование — сначала в Тулузе (1620—1625), а затем в Бордо и Орлеане (1625—1631).

В 1631 году, успешно окончив обучение, Ферма выкупил должность королевского советника парламента (другими словами, члена высшего суда) в Тулузе. В этом же году он женился на дальней родственнице матери, Луизе де Лонг. У них было пятеро детей^[4].

Памятник Ферма в Бомон-де-Ломань.

Быстрый служебный рост позволил Ферма стать членом Палаты эдиктов в городе Кастр (1648). Именно этой должности он обязан добавлением к своему имени признака знатности — частицы de; с этого времени он становится Пьером де Ферма.

Спокойная размеренная жизнь провинциального юриста оставляла Ферма время на самообразование и математические исследования. В 1636 году он написал трактат «Введение к теории плоских и пространственных мест», где независимо от «Геометрии» Декарта (вышедшей годом позже) изложил аналитическую геометрию. В 1637 году сформулировал свою «Великую теорему». В 1640 году обнародовал менее знаменитую, но гораздо более фундаментальную Малую теорему Ферма. Вёл активную переписку (через Марена Мерсенна) с крупными математиками того периода. С его переписки с Паскалем начинается формирование идей теории вероятностей.

В 1637 году начался конфликт Ферма и Декарта. Ферма уничтожающе отозвался о декартовой «Диоптрике», Декарт не остался в долгу, дал разгромный отзыв на работы Ферма по анализу и намекнул, что часть результатов Ферма являются плагиатом из декартовской «Геометрии». Метод Ферма для проведения касательных Декарт не понял (изложение в статье Ферма в самом деле было кратким и небрежным) и в качестве вызова предложил автору найти касательную к кривой, позднее названной «декартов лист». Ферма не замедлил дать два правильных решения — одно согласно статье Ферма, другое — основанное на идеях «Геометрии» Декарта, причём стало очевидным, что способ Ферма проще и удобнее. Посредником в споре выступил Жерар Дезарг — он признал, что метод Ферма универсален и правилен по существу, но изложен неясно и неполно. Декарт принёс извинения сопернику, но до конца жизни относился к Ферма недоброжелательно

[5].

Около 1652 года Ферма пришлось опровергать сообщение о своей кончине во время эпидемии чумы; он действительно заразился, но выжил, причём смерть множества коллег продвинула Ферма до поста высшего парламентского судьи. В 1654 году Ферма совершил единственное в своей жизни дальнее путешествие по Европе. В 1660 году планировалась его встреча с Паскалем, но из-за плохого здоровья обоих учёных встреча не состоялась^[4].

Пьер де Ферма умер 12 января 1665 года в городе Кастр, во время выездной сессии суда. Первоначально его похоронили там же, в Кастре, но позднее (1675) прах перенесли в семейную усыпальницу Ферма в тулузской церкви августинцев. В годы Французской революции останки Ферма затерялись.

Старший сын учёного, Клеман-Самуэль (также любитель математики), издал в 1670 году посмертное собрание трудов отца (несколько сотен писем и заметок), из которого научная общественность и узнала о замечательных открытиях Пьера Ферма. Дополнительно он опубликовал «Комментарии к Диофанту», сделанные отцом на полях перевода книги Диофанта; с этого момента начинается известность «Великой теоремы Ферма»^[6].

Современники характеризуют Ферма как честного, аккуратного, уравновешенного и приветливого человека, блестяще эрудированного как в математике, так и в гуманитарных науках, знатока многих древних и живых языков, на которых он писал неплохие стихи

[7].

Бюст Ферма в тулузском Капитолии

Открытия Ферма дошли до нас благодаря сборнику его обширной переписки (в основном через Мерсенна), изданной посмертно сыном учёного. Ферма приобрёл славу одного из первых математиков Франции, хотя и не писал книг (научных журналов ещё не было), ограничиваясь письмами к коллегам. Среди его корреспондентов были Рене Декарт, Блез Паскаль, Жерар Дезарг, Жиль Роберваль, Джон Валлис и другие. Единственной работой Ферма, опубликованной в печатном виде при его жизни, стал «Трактат о спрямлении» (1660), который вышел в свет как приложении к труду его земляка и друга Антуана де Лалувера и (по требованию Ферма) без указания имени автора.

В отличие от Декарта и Ньютона, Ферма был чистым математиком — первым великим математиком новой Европы. Независимо от Декарта он создал аналитическую геометрию. Раньше Ньютона умел использовать дифференциальные методы для проведения касательных, нахождения максимумов и вычисления площадей. Правда, Ферма, в отличие от Ньютона, не свёл эти методы в систему, однако Ньютон позже признавался, что именно работы Ферма подтолкнули его к созданию анализа

[8].

Главная же заслуга Пьера Ферма — создание теории чисел.

Теория чисел[править | править код]

Математики Древней Греции со времён Пифагора собирали и доказывали разнообразные утверждения, относящиеся к натуральным числам (например, методы построения всех пифагоровых троек, метод построения совершенных чисел и т. п.). Диофант Александрийский (III век н. э.) в своей «Арифметике» рассматривал многочисленные задачи о решении в рациональных числах алгебраических уравнений с несколькими неизвестными (ныне диофантовыми принято называть уравнения, которые требуется решить в целых числах). Эта книга (не полностью) стала известна в Европе в XVI веке, а в 1621 году она была издана во Франции и стала настольной книгой Ферма.

Ферма постоянно интересовался арифметическими задачами, обменивался сложными задачами с современниками. Например, в своём письме, получившем название «Второго вызова математикам» (февраль 1657), он предложил найти общее правило решения уравнения Пелля ax2+1=y2{\displaystyle ax^{2}+1=y^{2}} в целых числах. В письме он предлагал найти решения при a=149, 109, 433. Полное решение задачи Ферма было найдено лишь в 1759 году Эйлером.

Начал Ферма с задач про магические квадраты и кубы, но постепенно переключился на закономерности натуральных чисел — арифметические теоремы. Несомненно влияние Диофанта на Ферма, и символично, что он записывает свои удивительные открытия на полях «Арифметики».

Ферма обнаружил, что если a не делится на простое число p, то число ap−1−1{\displaystyle a^{p-1}-1} всегда делится на p (см. Малая теорема Ферма). Позднее Эйлер дал доказательство и обобщение этого важного результата: см. Теорема Эйлера.

Обнаружив, что число 22k+1{\displaystyle 2^{2^{k}}+1} простое при k ≤ 4, Ферма решил, что эти числа простые при всех k, но Эйлер впоследствии показал, что при k=5 имеется делитель 641. До сих пор неизвестно, конечно или бесконечно множество простых чисел Ферма.

Эйлер доказал (1749) ещё одну гипотезу Ферма (сам Ферма редко приводил доказательства своих утверждений): простые числа вида 4k+1 представляются в виде суммы квадратов (5=4+1; 13=9+4), причём единственным способом, а для чисел, содержащих в своём разложении на простые множители простые числа вида 4k+3 в нечётной степени, такое представление невозможно. Эйлеру это доказательство стоило 7 лет трудов; сам Ферма доказывал эту теорему косвенно, изобретённым им индуктивным «методом бесконечного спуска». Этот метод был опубликован только в 1879 году; впрочем, Эйлер восстановил суть метода по нескольким замечаниям в письмах Ферма и неоднократно успешно его применял. Позже усовершенствованную версию метода применяли Пуанкаре и Андре Вейль.

Ферма разработал способ систематического нахождения всех делителей числа, сформулировал теорему о возможности представления произвольного числа суммой не более четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов). Самое знаменитое его утверждение — «Великая теорема Ферма» (см. ниже).

Большой интерес вызывали у Ферма фигурные числа. В 1637 году он сформулировал так называемую «золотую теорему»^[9]:

Этой теоремой занимались многие выдающиеся математики, полное доказательство сумел дать Коши в 1813 году^[10].

Многие остроумные методы, применяемые Ферма, остались неизвестными. Однажды Мерсенн попросил Ферма выяснить, является ли многозначное число 100 895 598 169 простым. Ферма не замедлил сообщить, что 100895598169=898423⋅112303;{\displaystyle 100895598169=898423\cdot 112303;} он не пояснил, как нашёл эти делители.

Арифметические открытия Ферма опередили время и были забыты на 70 лет, пока ими не заинтересовался Эйлер, опубликовавший систематическую теорию чисел. Одна из причин этого — интересы большинства математиков переключились на математический анализ; сказалось, вероятно, и то, что Ферма использовал устаревшую и громоздкую математическую символику Виета вместо гораздо более удобных обозначений Декарта^[11].

Математический анализ и геометрия[править | править код]

Ферма практически по современным правилам находил касательные к алгебраическим кривым. Именно эти работы подтолкнули Ньютона к созданию анализа^[8]. В учебниках по математическому анализу можно найти важную лемму Ферма, или необходимый признак экстремума: в точках экстремума производная функции равна нулю.

Ферма сформулировал общий закон дифференцирования дробных степеней. Он дал общий способ для проведения касательных к произвольной алгебраической кривой. В «Трактате о квадратурах» (1658) Ферма показал, как найти площадь под гиперболами различных степеней, распространив формулу интегрирования степени даже на случаи дробных и отрицательных показателей. В «Трактате о спрямлении» Ферма описал общий способ решения труднейшей задачи нахождения длины произвольной (алгебраической) кривой.

Наряду с Декартом, Ферма считается основателем аналитической геометрии. В работе «Введение к теории плоских и пространственных мест», ставшей известной в 1636 году, он первый провёл классификацию кривых в зависимости от порядка их уравнения, установил, что уравнение первого порядка определяет прямую, а уравнение второго порядка — коническое сечение. Развивая эти идеи, Ферма пошёл дальше Декарта и попытался применить аналитическую геометрию к пространству, но существенно не продвинулся в этой теме.

Другие достижения[править | править код]

Независимо от Паскаля Ферма разработал основы теории вероятностей. Именно с переписки Ферма и Паскаля (1654), в которой они, в частности, пришли к понятию математического ожидания и теоремам сложения и умножения вероятностей, отсчитывает свою историю эта замечательная наука. Результаты Ферма и Паскаля были приведены в книге Гюйгенса «О расчётах в азартной игре» (1657), первом руководстве по теории вероятностей.

Имя Ферма носит основной вариационный принцип геометрической оптики, в силу которого свет в неоднородной среде выбирает путь, занимающий наименьшее время (впрочем, Ферма считал, что скорость света бесконечна, и формулировал принцип более туманно). С этого тезиса начинается история главного закона физики — принципа наименьшего действия.

Ферма перенёс на трёхмерный случай (внутреннего касания сфер) алгоритм Виета для задачи Аполлония касания окружностей^[12].

Великая теорема Ферма[править | править код]

Ферма широко известен благодаря так называемой великой (или последней) теореме Ферма. Теорема была сформулирована им в 1637 году, на полях книги «Арифметика» Диофанта с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы привести его на полях.

Вероятнее всего, его доказательство не было верным, так как позднее он опубликовал доказательство только для случая n=4{\displaystyle n=4}. Доказательство, разработанное в 1994 году Эндрю Уайлсом, содержит 129 страниц и опубликовано в журнале «Annals of Mathematics» в 1995 году.

Простота формулировки этой теоремы привлекла много математиков-любителей, так называемых ферматистов. Даже и после решения Уайлса во все академии наук идут письма с «доказательствами» великой теоремы Ферма.

• В 1935 г. Международный астрономический союз присвоил имя Пьера Ферма кратеру на видимой стороне Луны.
• Математическая премия Ферма вручается с 1989 года.
• В Тулузе имя Ферма присвоено улице, а также старейшему и самому престижному лицею Тулузы (Lycée Pierre de Fermat).
• В Бомон-де-Ломани, где родился Ферма, открыт его музей и установлен памятник учёному. В его честь названы улица и расположенный на этой улице отель.
• В честь Ферма названы различные математические теоремы и понятия, в том числе:

Великая теорема Ферма

Малая теорема Ферма

Метод факторизации Ферма

Проблема Штейнера

Спираль Ферма

Точка Ферма

Числа Ферма

Ферма в художественной литературе и на марках[править | править код]

Александр Казанцев написал научно-фантастический роман-гипотезу «Клокочущая пустота», Книга первая этого романа «Острее шпаги» посвящена описанию жизни и достижений Пьера Ферма.

В год 400-летия учёного (2001) почта Франции выпустила почтовую марку (0,69 евро) с его портретом и формулировкой Великой теоремы.

1. ↑ http://www.nytimes.com/1983/07/19/science/german-is-hailed-in-math-advance.html
2. ↑ Архив по истории математики Мактьютор
3. ↑ Альварес, 2015, с. 15.
4. ↑ ^{1 2} Стиллвелл Д. Математика и её история. — Москва-Ижевск: Институт компьютерных исследований, 2004, стр. 211—212.
5. ↑ Альварес, 2015, с. 124—128.
6. ↑ Альварес, 2015, с. 40.
7. ↑ Белл Э. Т. Творцы математики, 1979, с. 58.
8. ↑ ^{1 2} Вавилов С. И. Исаак Ньютон. 2-е дополненное издание. М.-Л.: Изд. АН СССР, 1945 г., глава 13.
9. ↑ Матвиевская Г. П. Учение о числе на средневековом Ближнем и Среднем Востоке. — Ташкент: ФАН, 1967. — С. 22—23. — 344 с..
10. ↑ Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975. — С. 10—11. — 208 с.
11. ↑ Альварес, 2015, с. 91.
12. ↑ Барабанов О. О., Барабанова Л. П. Алгоритмы решения навигационной разностно-дальномерной задачи — от Аполлония до Коши // История науки и техники, 2008, № 11, С.2-21.

• Ферма П. Исследования по теории чисел и диофантову анализу. М.: Наука, 1992. ISBN 5-02-014121-6. Переиздания: 2007, 2015.

• Альварес Л. Ф. А. Самая сложная задача в мире. Ферма. Великая теорема Ферма // Наука. Величайшие теории. — М.: Де Агостини, 2015. — Вып. 18. — ISSN 2409-0069.
• Башмакова И. Г. Диофант и Ферма (к истории метода касательных и экстремумов). Историко-математические исследования, 17, 1966, С. 185—207.
• Башмакова И. Г., Славутин Е. И. История диофантова анализа от Диофанта до Ферма. М.: Наука, 1984.
• Белл Э. Т. Творцы математики. — М.: Просвещение, 1979. — 256 с.
• Ван дер Варден Б. Л. Переписка между Паскалем и Ферма по вопросам теории вероятностей. ИМИ, 21, 1976, С. 228—232.
• Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
• Ферма // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Фрейман Л. С. Ферма, Торричелли, Роберваль. В кн.: У истоков классической науки. М.: Наука, 1968, С. 173—254.
• Храмов Ю. А. Ферма Пьер (Pierre de Fermat) // Физики: Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. — С. 275. — 400 с. — 200 000 экз. (в пер.)
• Шаль. Исторический обзор происхождения и развития геометрических методов. Гл. 2, § 10-14. М., 1883.