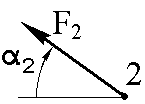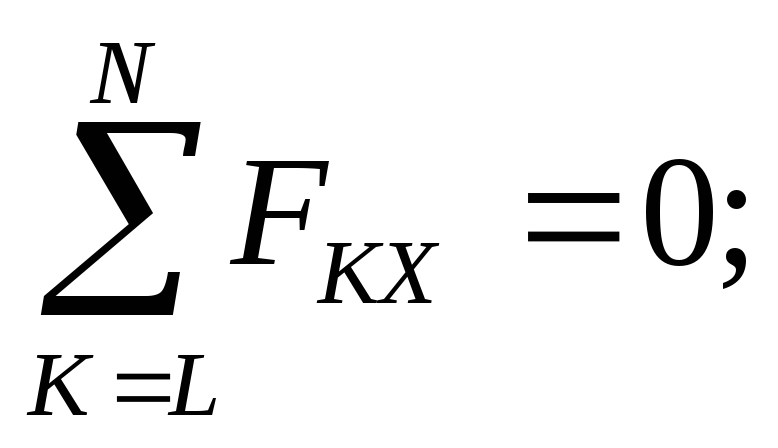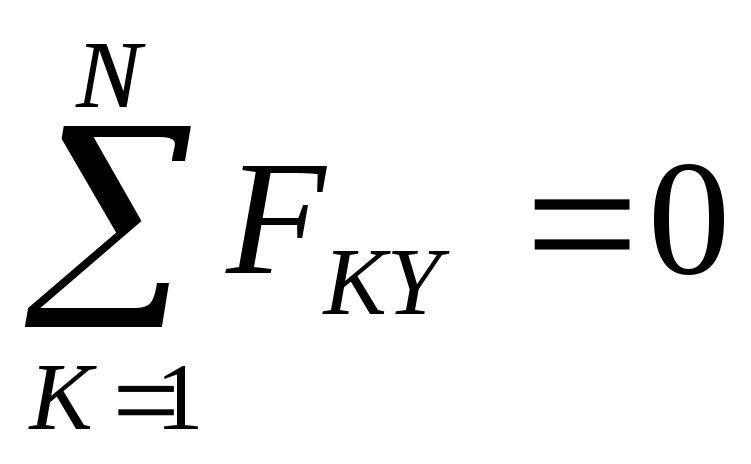статика5
Лекция 5
РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
Равновесие системы тел.
Расчет плоских ферм.
Равновесие при наличии трения скольжения. Законы Амонтона -Кулона.
Равновесие при наличии трения качения.
Равновесие системы тел
Если в равновесии находится не одно тело, а система тел, то для определения всех неизвестных величин необходимо расчленять систему, вводя в рассмотрение реакции внутренних связей. При этом возможны два способа составлений уравнений равновесия. Проиллюстрируем их применение на примере равновесия двух тел.
П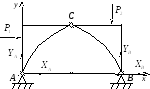

Количество неизвестных реакций внешних связей превышает количество уравнений равновесия плоской системы сил.
В этом случае помимо трех уравнений равновесия конструкции в целом составляются три дополнительных уравнения равновесия одной из частей конструкции.
Второй способ (рассмотреть равновесие каждой части конструкции):
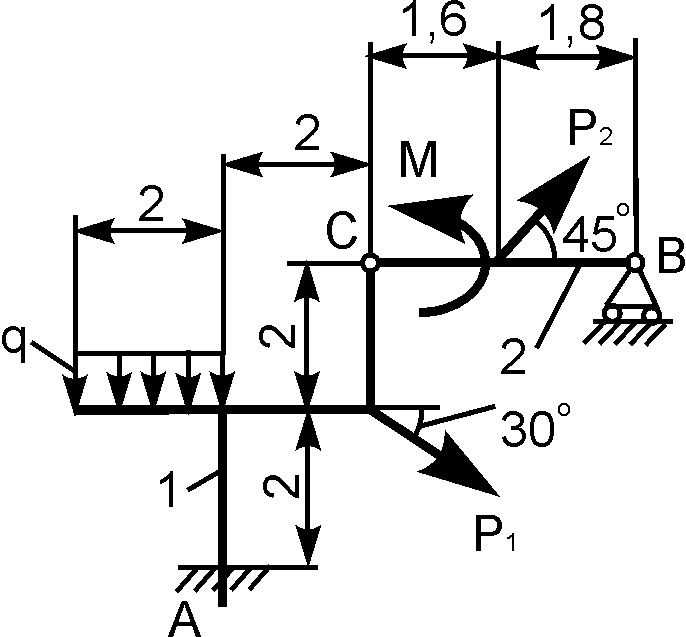
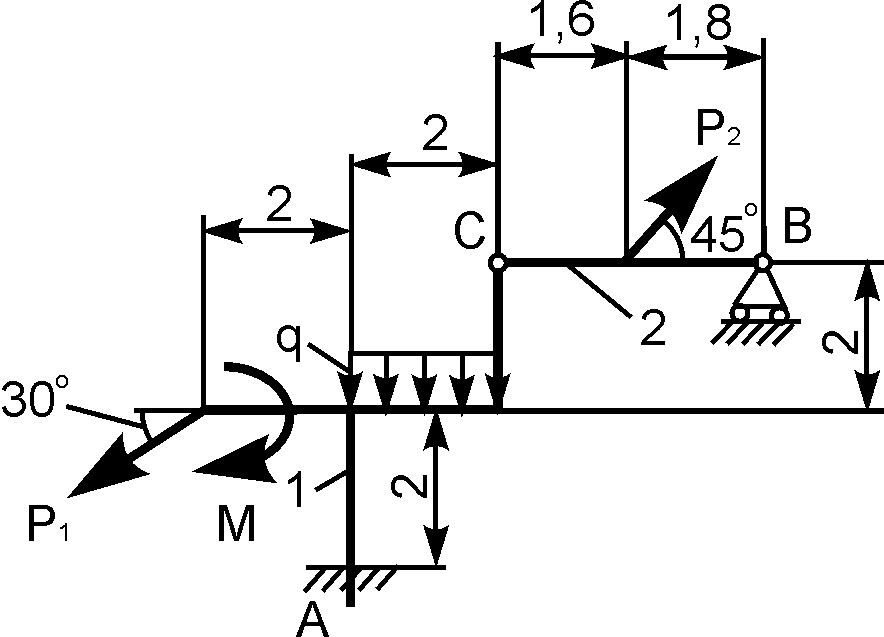
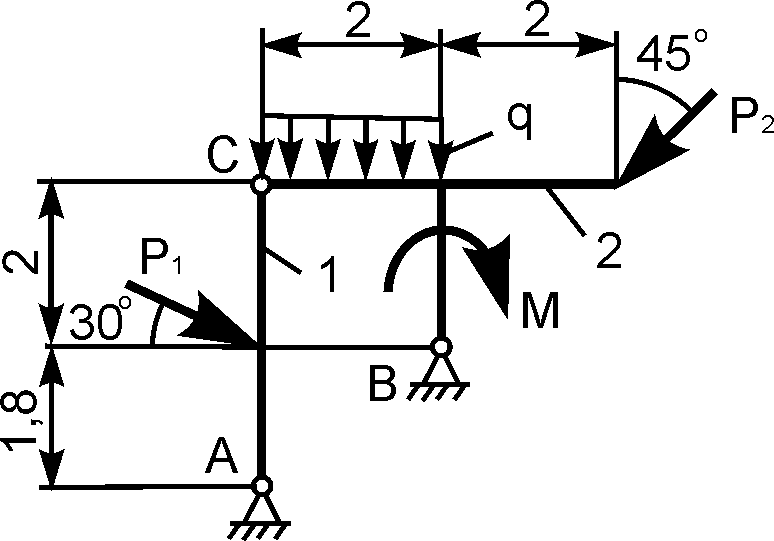
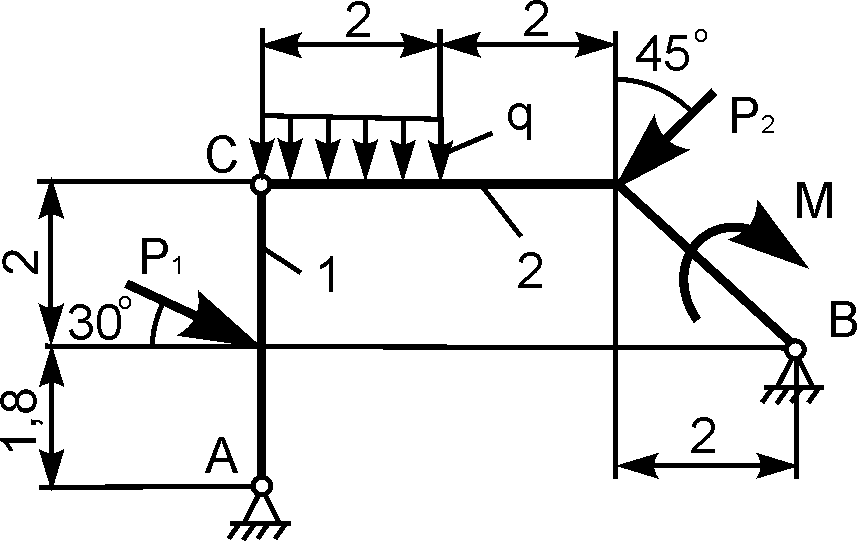
Пример:
Дано: 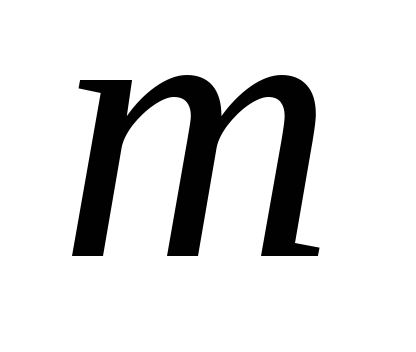 ,
, 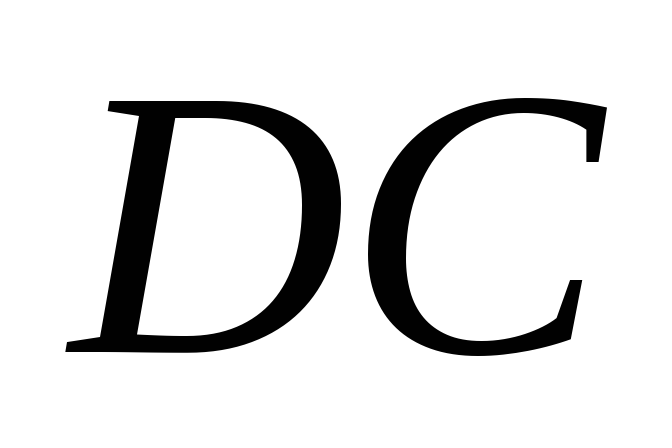 ,
, 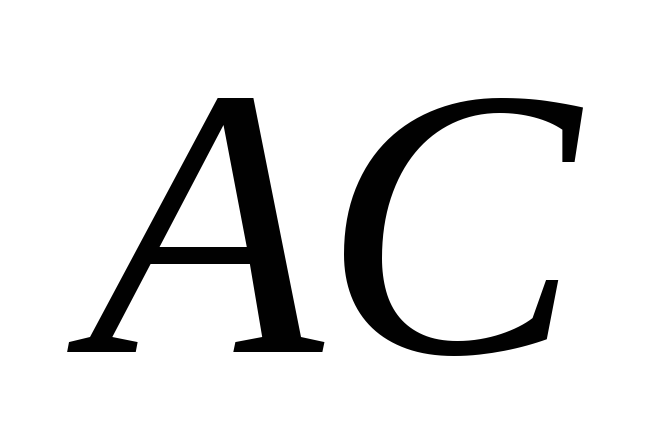
 . Найти:
реакции опор.
. Найти:
реакции опор.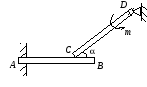
Р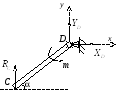 ассмотрим
равновесие балки CD:
ассмотрим
равновесие балки CD:
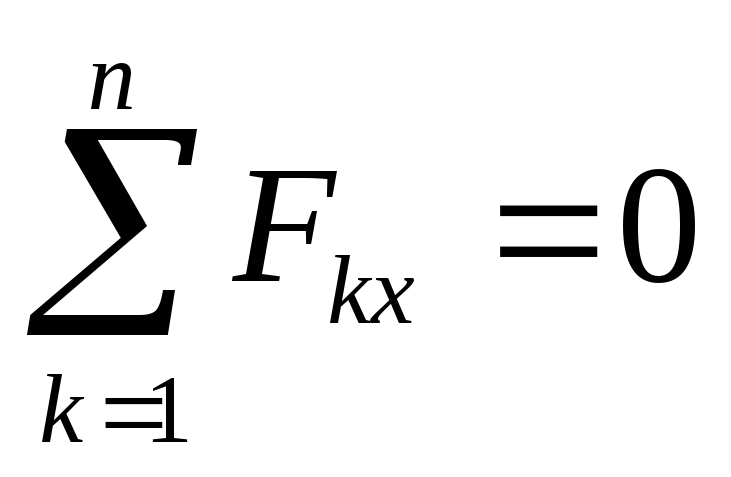

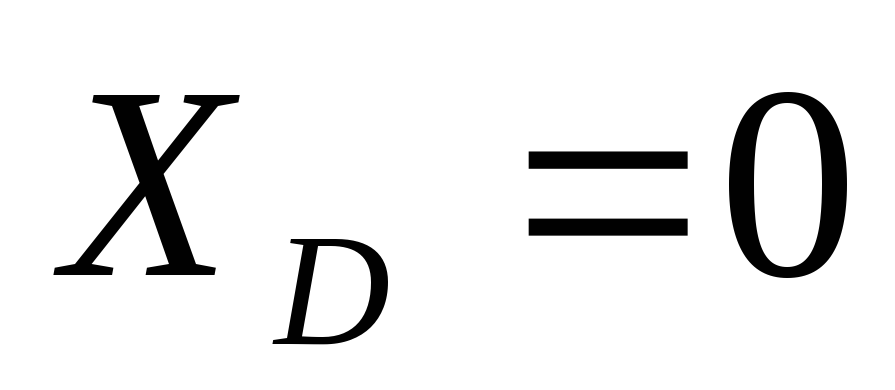 ,
,
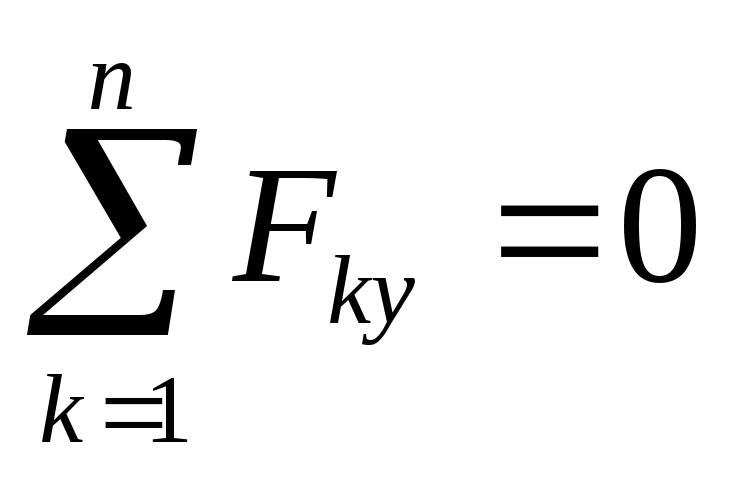
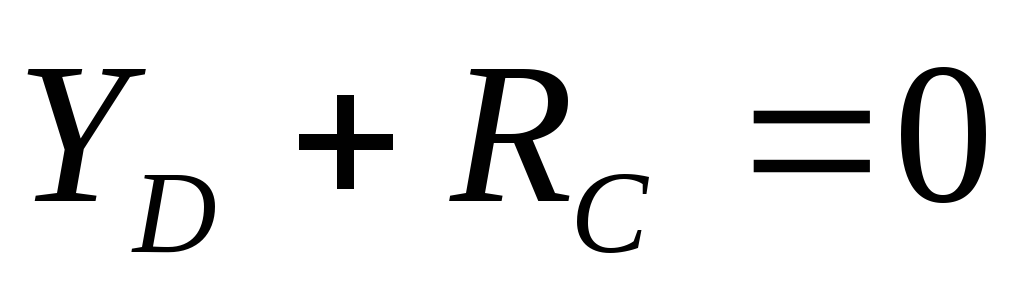 ,
,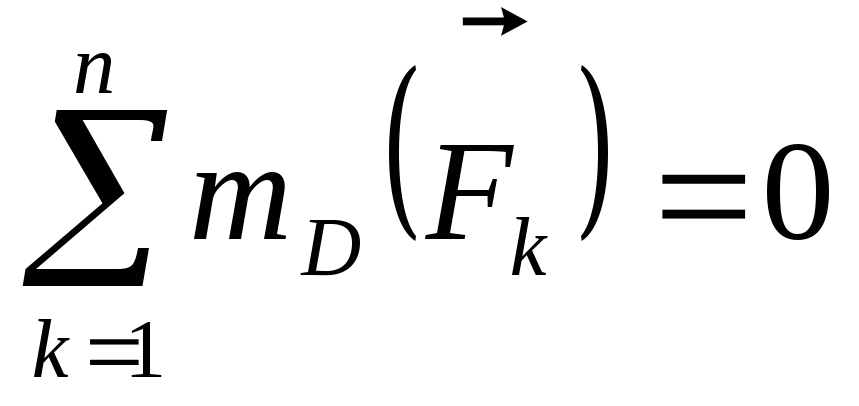
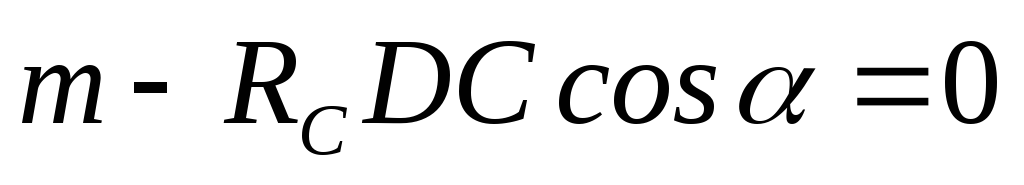 .
.
Рассмотрим равновесие балки AB:
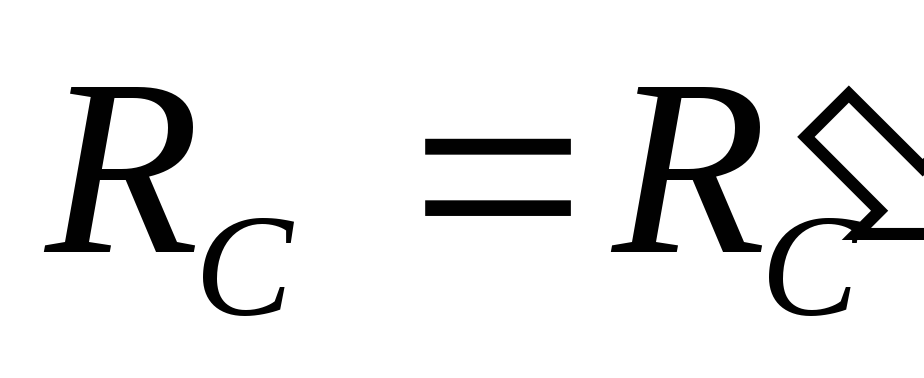 ,
,
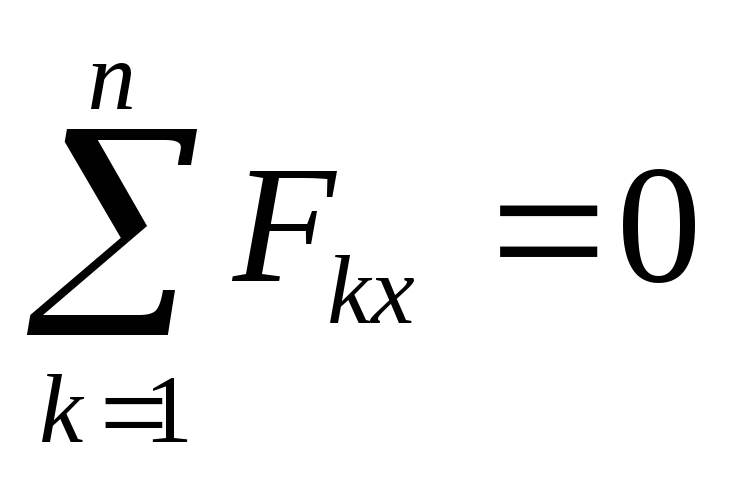

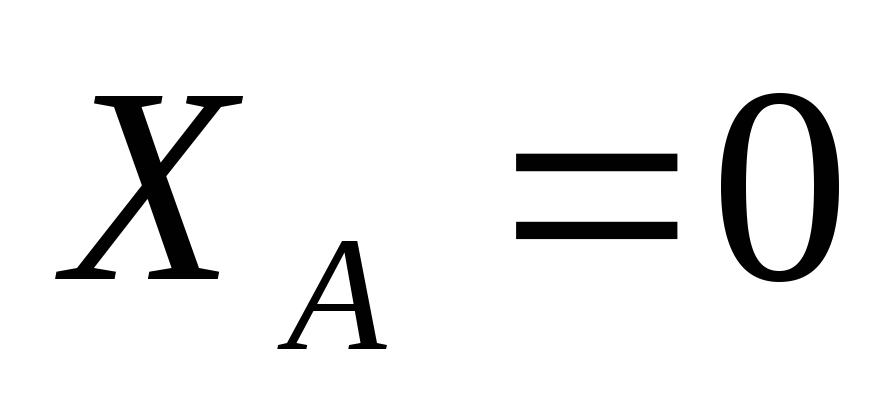 ,
,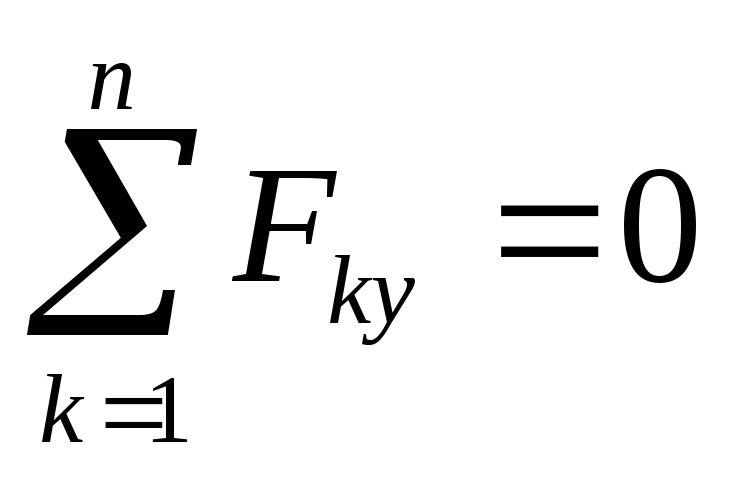
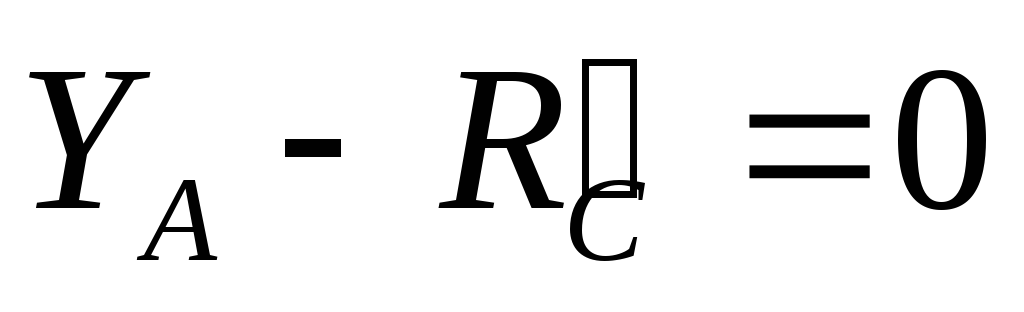 ,
,
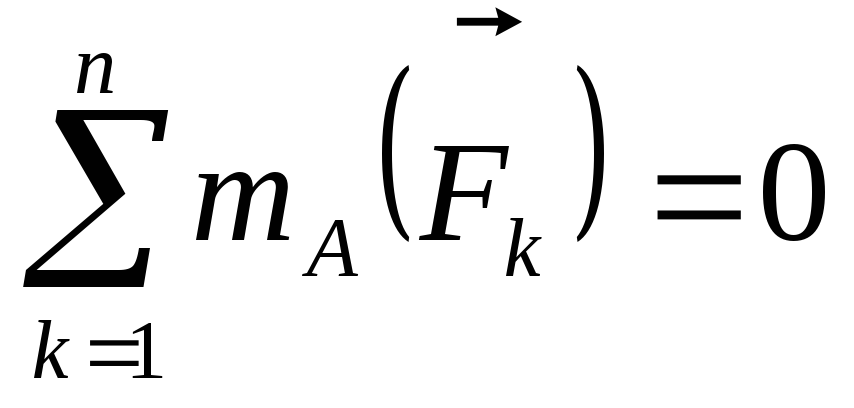
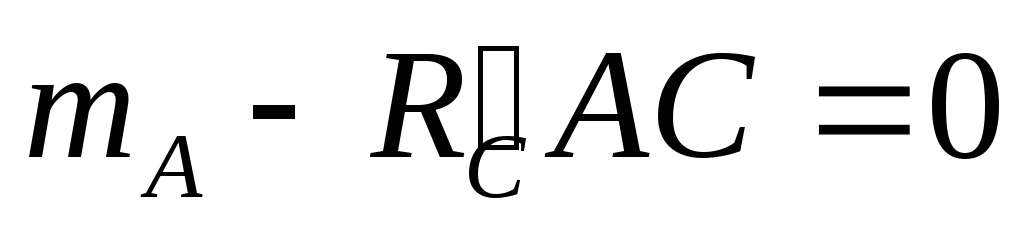 .
.
Решая систему шести уравнений, находим неизвестные реакции связей.
Способ выбираем из соображений удобства решения системы уравнений равновесия.
Ферма жесткая (геометрически неизменяемая) конструкция из стержней, соединенных между собой шарнирами. Шарнирные соединения называются узлами.
Задачей расчета ферм является определение реакций внешних связей и усилий в стержнях. Основные допущения – это идеальность стержней фермы и распределение внешней нагрузки по ее узлам.
У статически
определимых ферм количество стержней s и количество
узлов n связаны
соотношением: 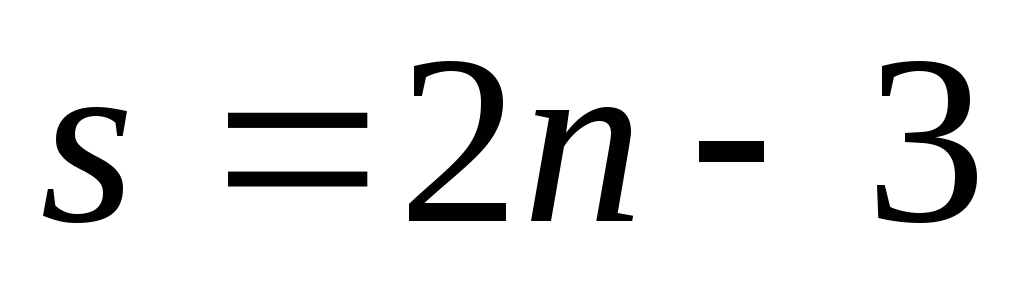 .
Это равенство получается из того факта,
что добавление к простейшей треугольной
ферме каждого нового узла требует двух
стержней :
.
Это равенство получается из того факта,
что добавление к простейшей треугольной
ферме каждого нового узла требует двух
стержней :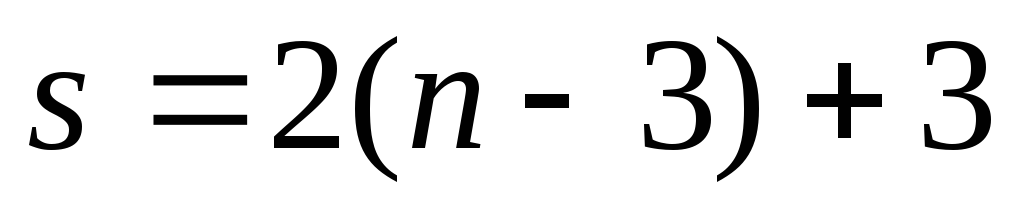
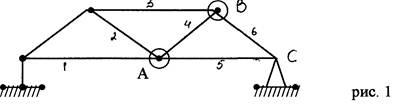
Основные методы расчета усилий в стержнях плоских ферм: метод вырезания узлов (последовательно вырезаются узлы, в которых сходится не более двух стержней с неизвестными усилиями, и составляются уравнения равновесия системы сходящихся сил) и метод сечений (Риттера1) (производится сечение фермы по трем стержням с неизвестными усилиями и составляются уравнения равновесия одной части фермы).
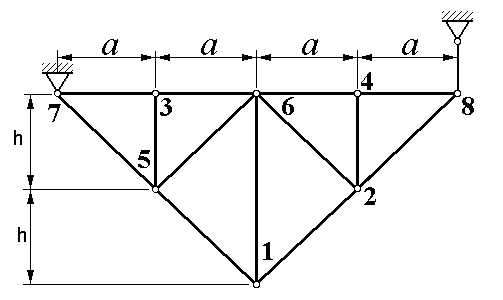
Пример:
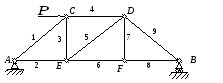
Дано: 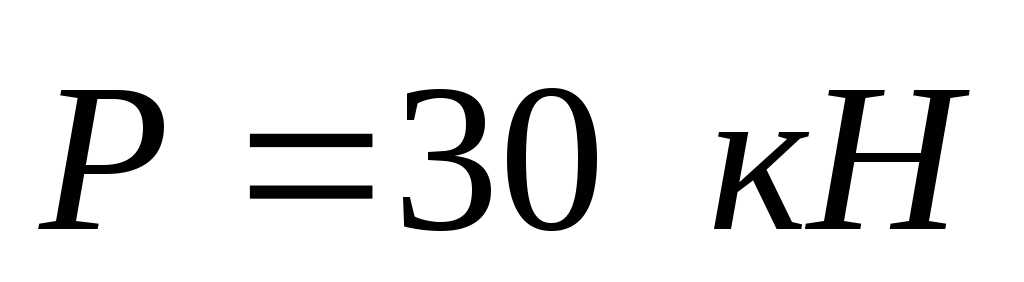
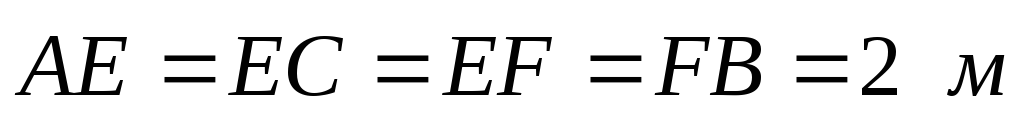 .
.Найти усилия в стержнях.
Вначале определим опорные реакции:
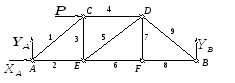
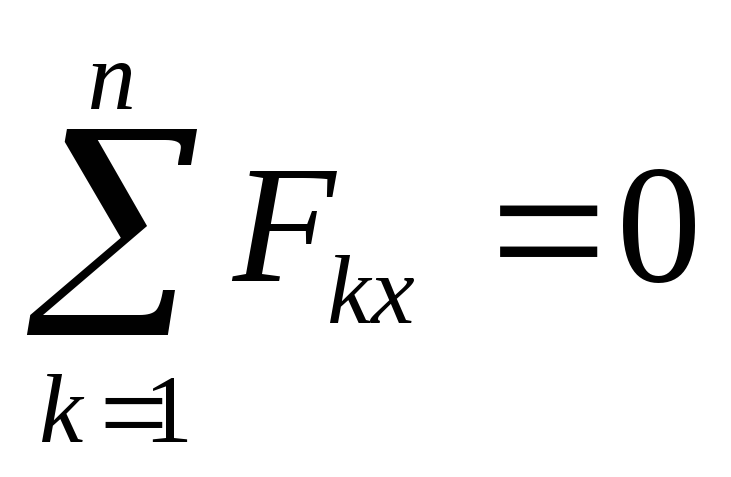

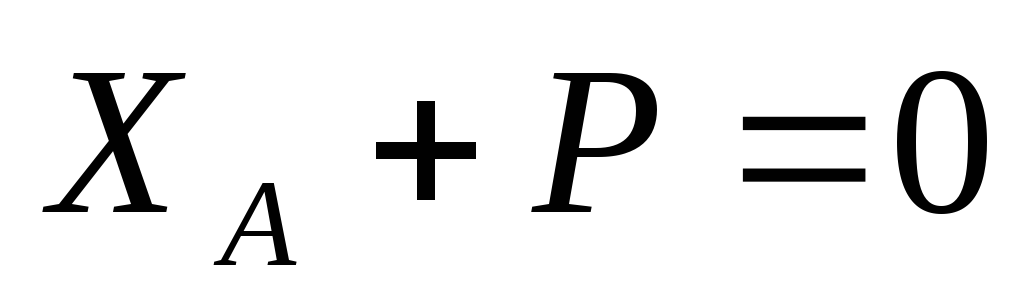 ,
,
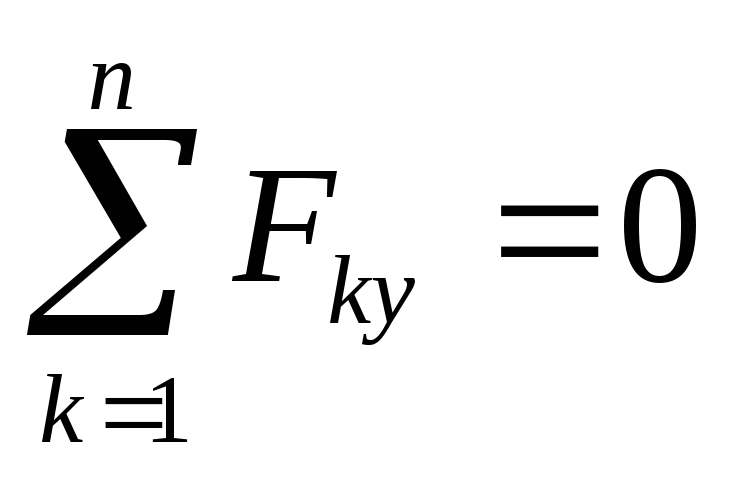
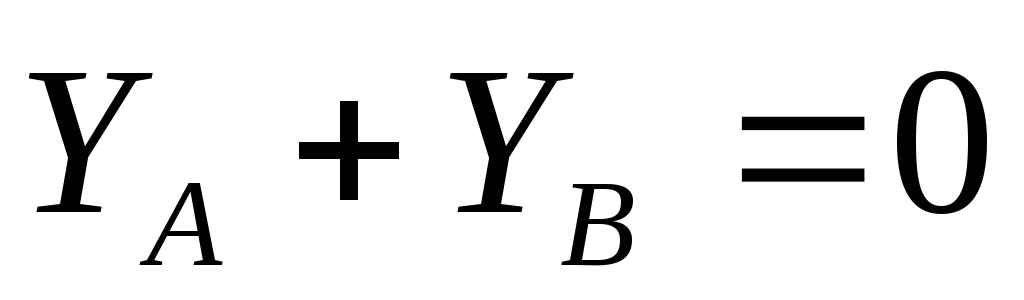
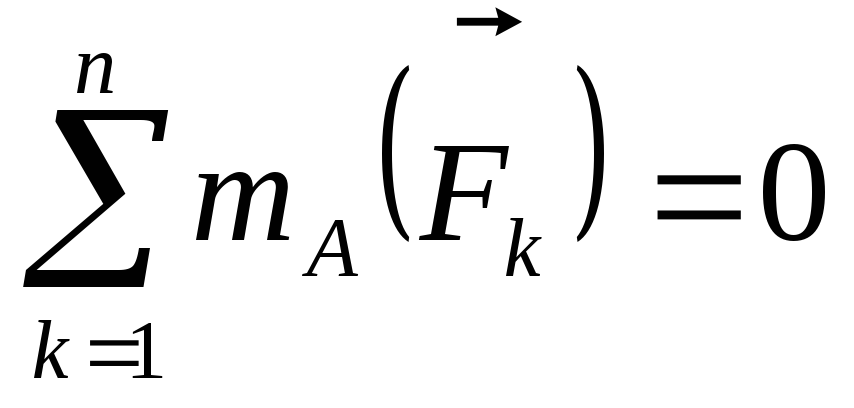
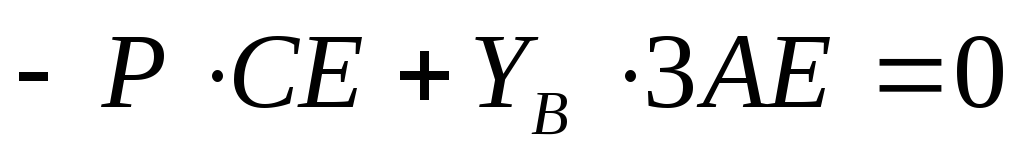 .
.
Отсюда 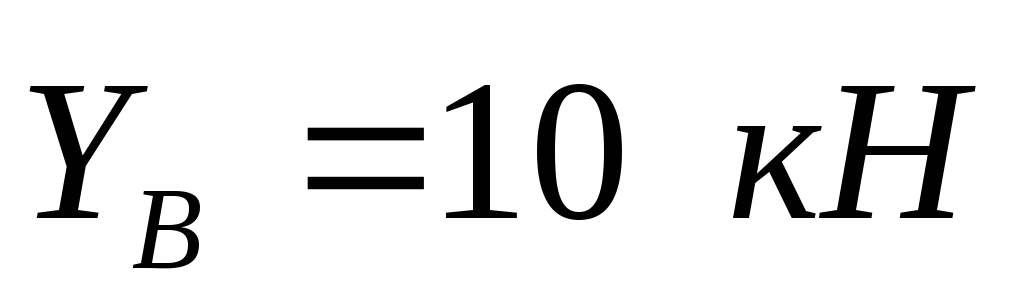 ,
, 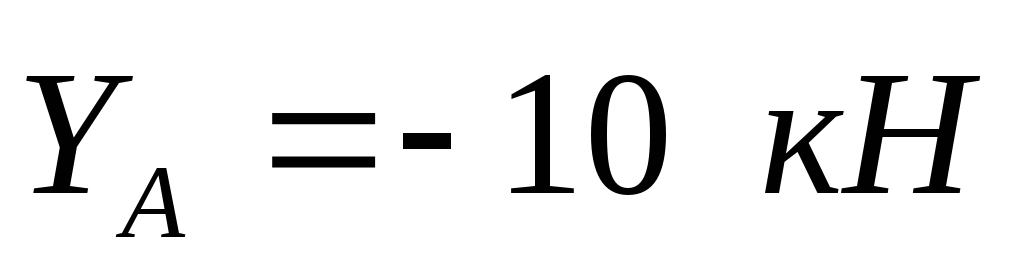 ,
, 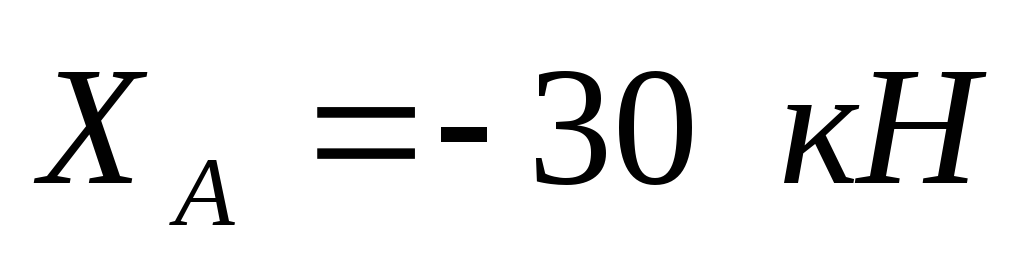 .
.
Определив реакции в т. А и в т. В, рассмотрим последовательно равновесие каждого узла, мысленно отбросив сходящиеся в них стержни и заменив их действия реакциями (усилиями). Полагая, что стержни растянуты, направим их усилия от узлов.
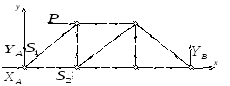
Покажем каждый узел в отдельности и составим уравнения их равновесия:
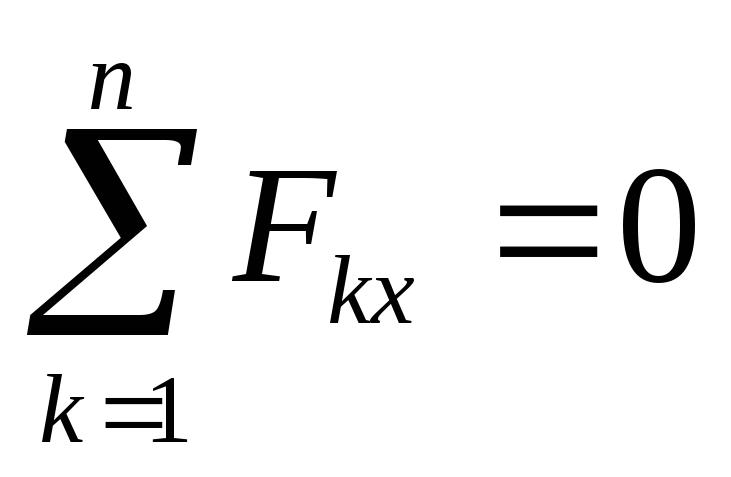

 ,
,
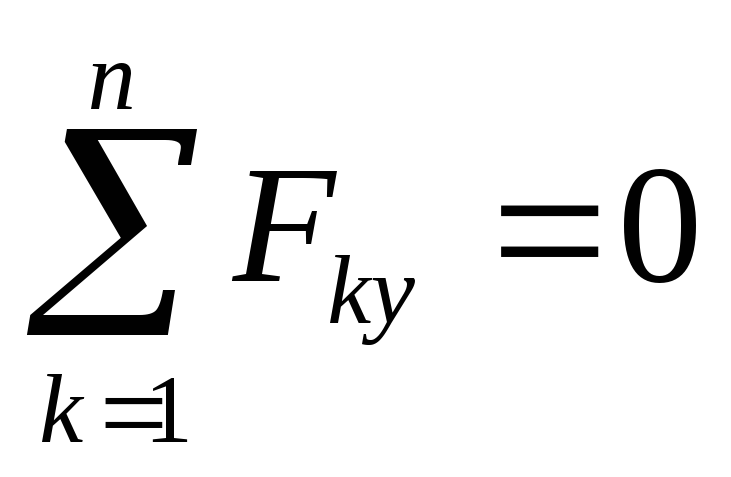
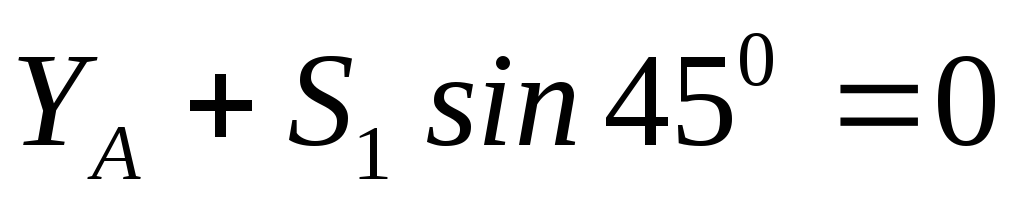 ,
,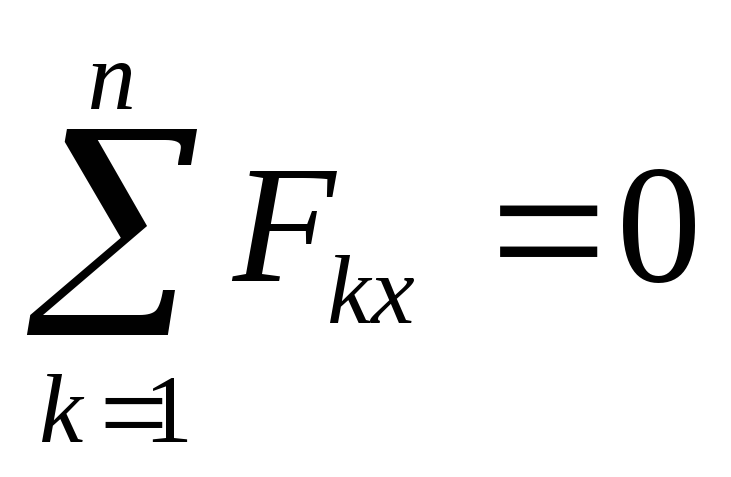
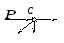

 ,
,
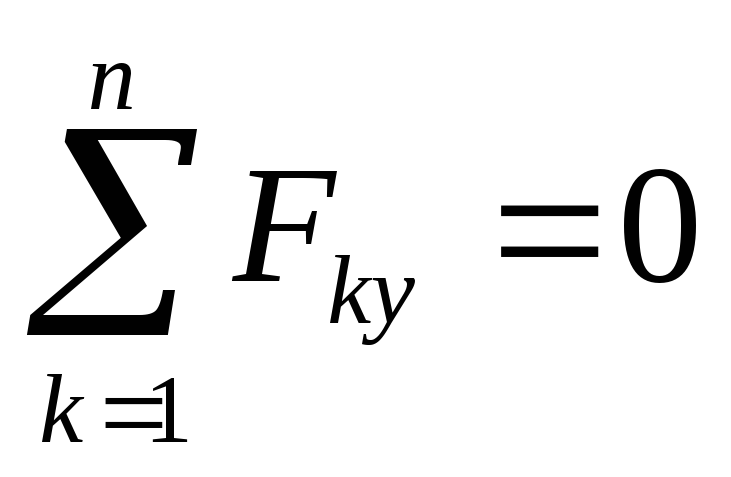
 ,
,
и т.д.
Для иллюстрации метода Риттера рассечем ферму по 4, 5 и 6 стержню и рассмотрим равновесие правой части. Действие отброшенной части фермы заменяется соответствующими реакциями.
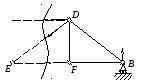
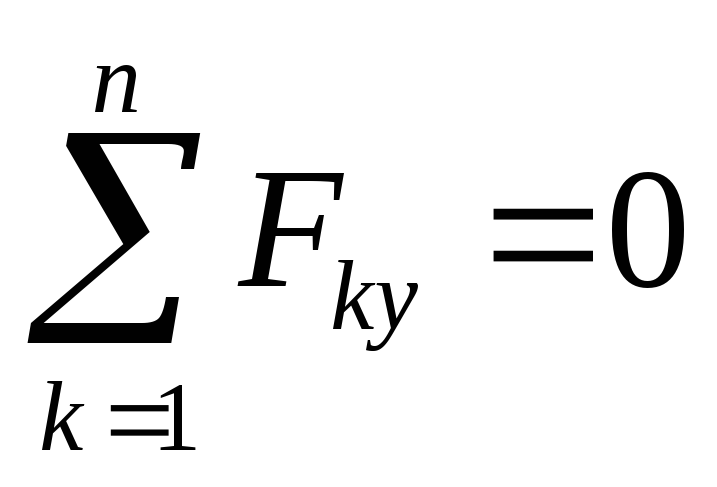
 ,
,
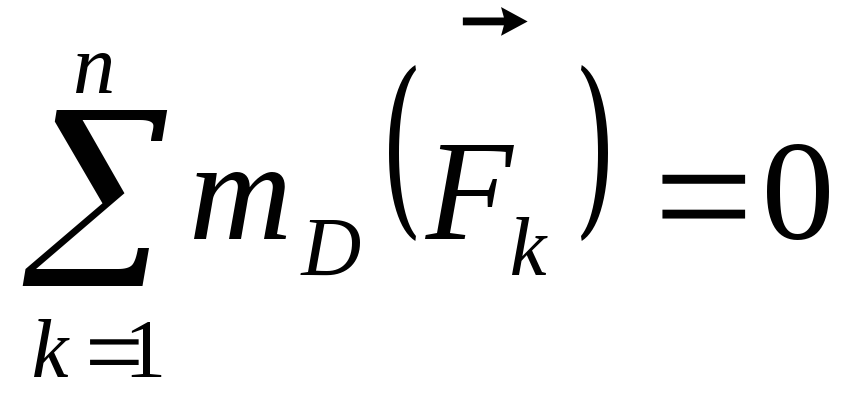

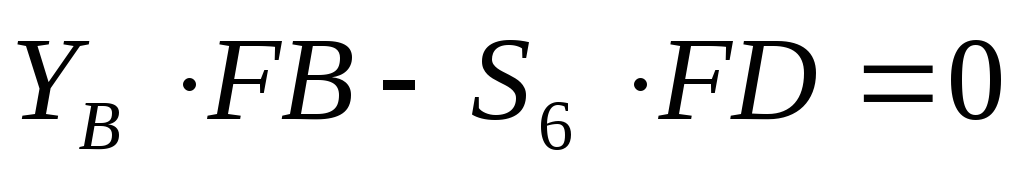 ,
,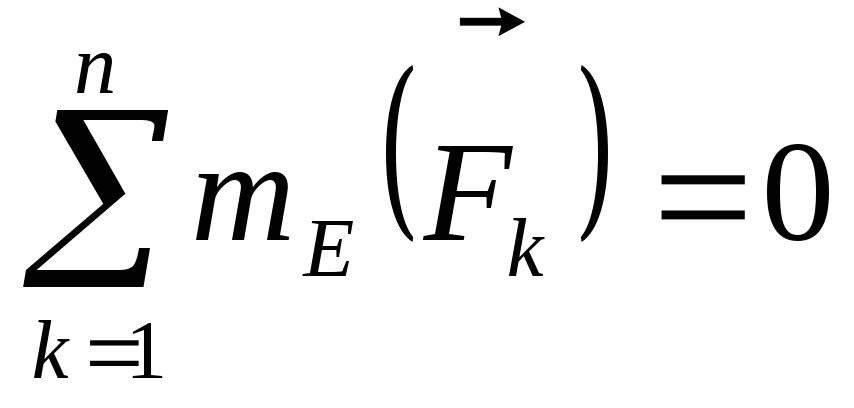
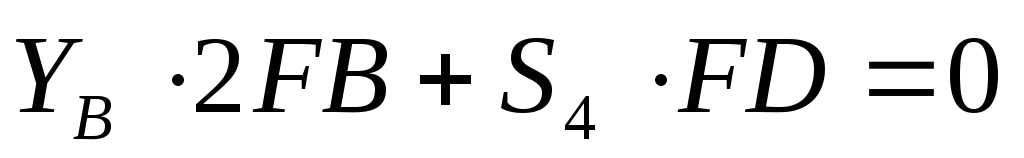 .
.
Получаем:
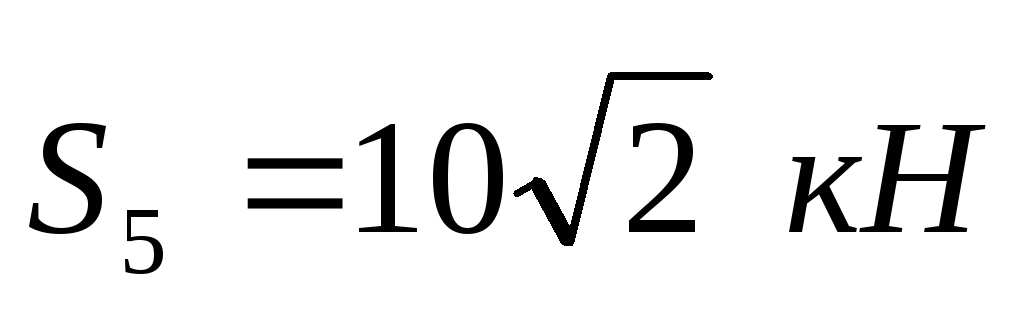 ,
, 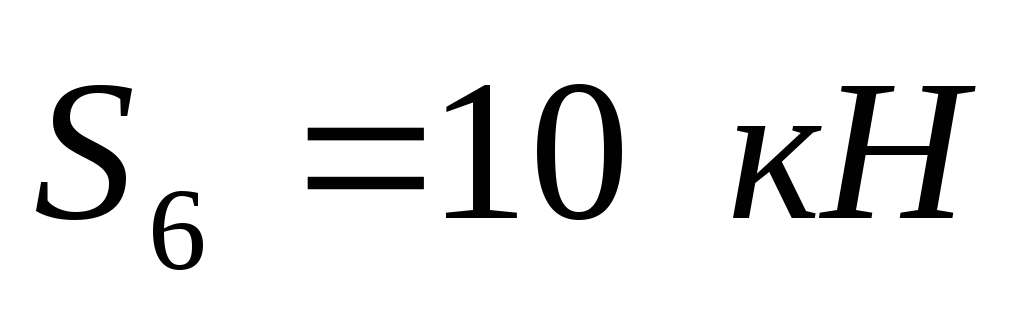 ,
, 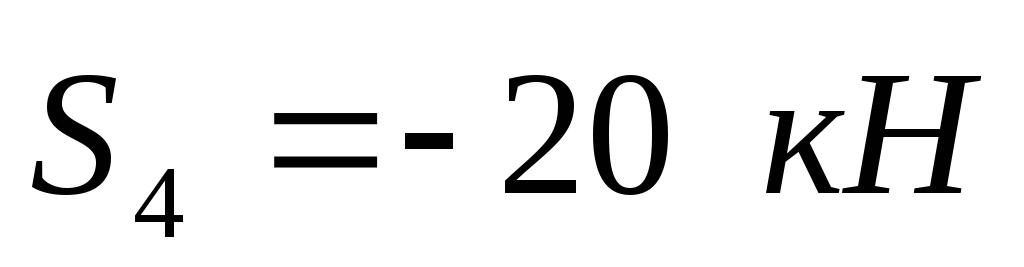 .
.
Знак минус означает, что соответствующий стержень работает на сжатие.
При определении усилий в стержнях по методу сечений составляются
уравнения рановесия, в каждое из которых входит по одной неизвестной.
Равновесие при наличии трения скольжения.
Законы Амонтона-Кулона
П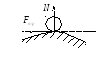 ри
стремлении сдвинуть тело, лежащее на
шероховатой поверхности, возникает
сила реакции, которая имеет две
составляющие – нормальную и силу
трения скольжения.
ри
стремлении сдвинуть тело, лежащее на
шероховатой поверхности, возникает
сила реакции, которая имеет две
составляющие – нормальную и силу
трения скольжения.
В результате экспериментальных исследований были установлены:
Законы Амонтона1 — Кулона2:
Сила трения скольжения при равновесии тела принимает значения от нуля до максимального значения.
Максимальное значение силы трения скольжения не зависит от площади контакта, а определяется величиной нормальной реакции, материалом и состоянием контактирующих поверхностей.
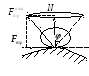 ,
где
,
где 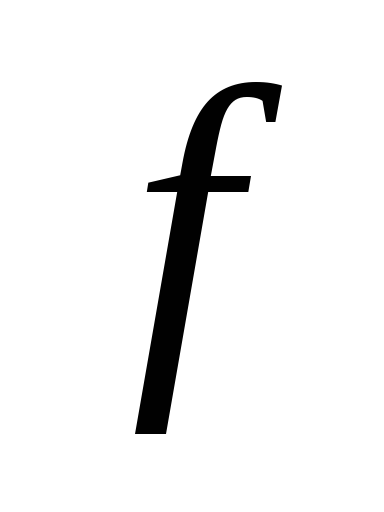 коэффициент
трения скольжения.
коэффициент
трения скольжения.
Конус трения поверхность, образованная линией действия максимальной реакции при стремлении сдвинуть тело в различных направлениях:
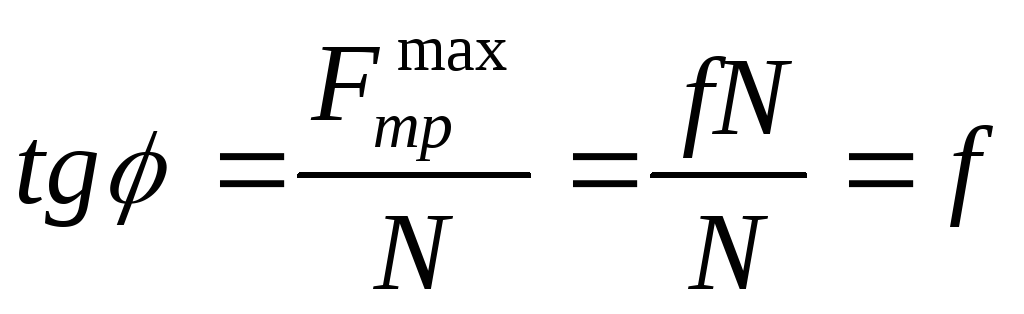
 ,
, 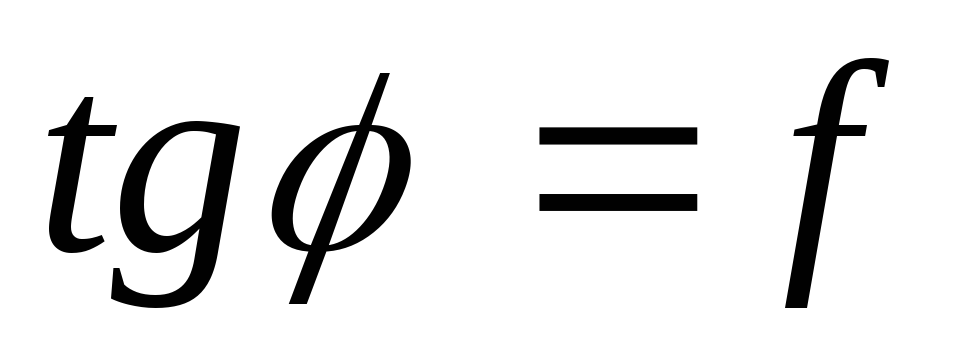 .
.
Рассмотрим равновесие тела на шероховатой поверхности под действием силы P.
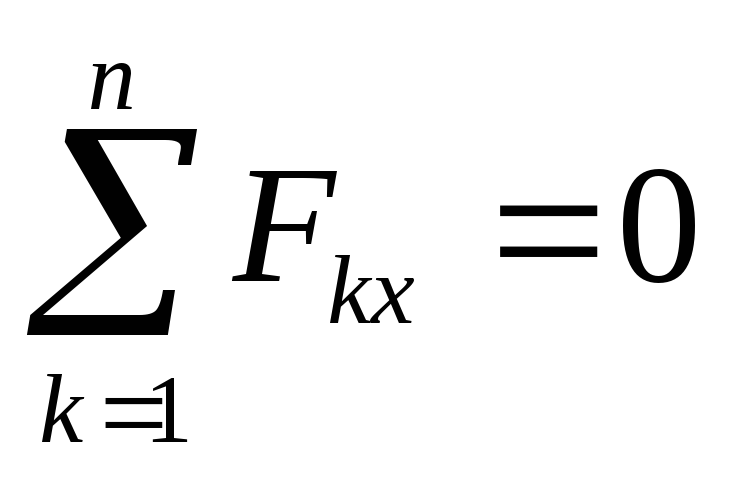
y

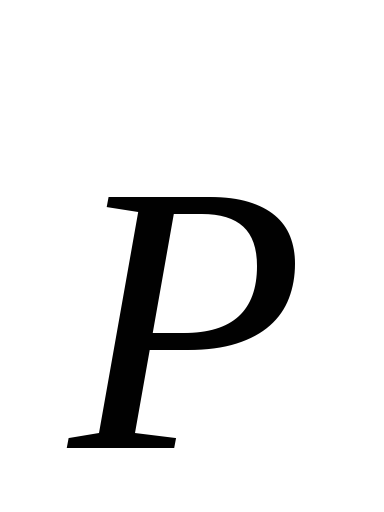
















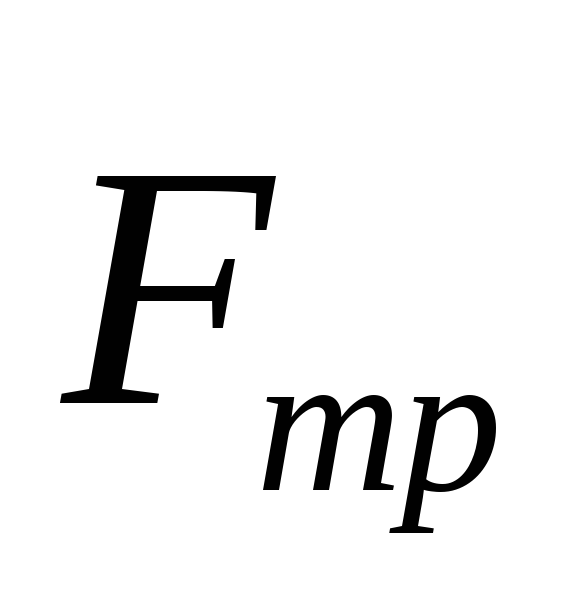


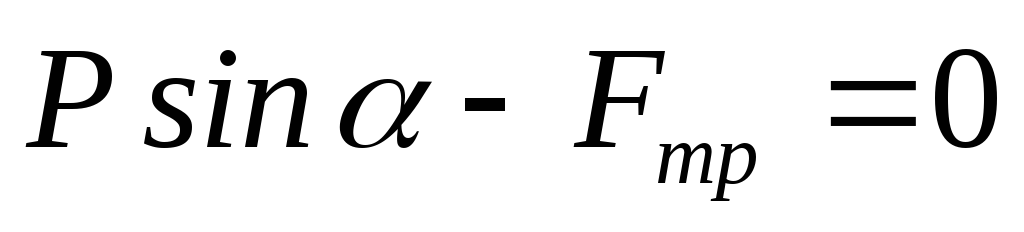 ,
,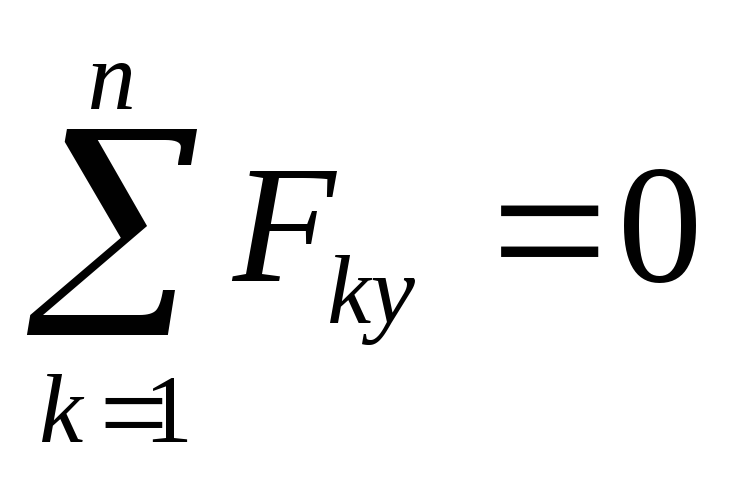
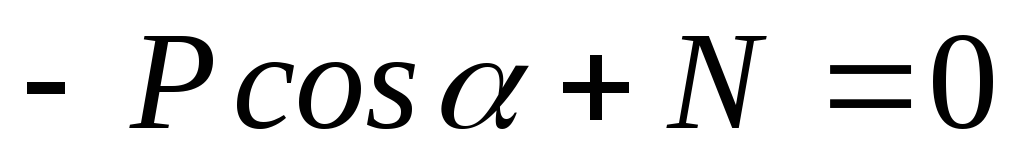 .
.
С
x
 ледовательно,
ледовательно, 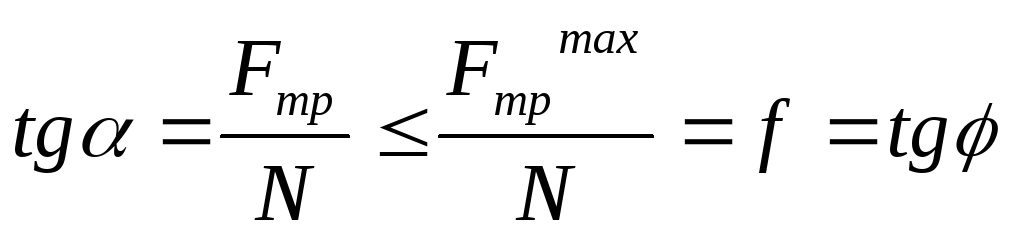 ,
,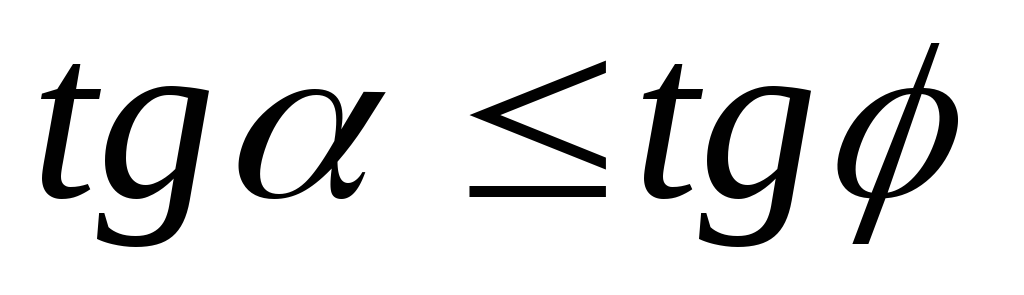 ,
, 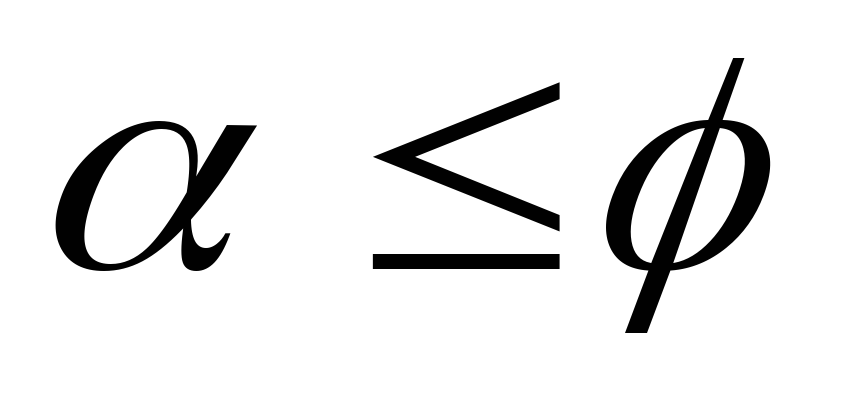 .
.
Никакая сила, лежащая внутри конуса трения, не может вывести тело из состояния покоя.
Равновесие при наличии трения качения
Т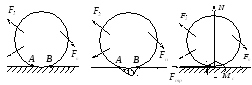 рением
качения называется сопротивление,
возникающее при качении одного тела по
поверхности другого.
рением
качения называется сопротивление,
возникающее при качении одного тела по
поверхности другого.
Вследствие деформации тел их касание происходит вдоль площадки AB и имеем распределенную систему сил реакции, которая может быть заменена силой и парой. Сила раскладывается на две составляющие — нормальную и силу трения скольжения. При равновесии тела момент сопротивления качению определяется из условий равновесия системы сил. При этом установлено, что момент сопротивления принимает значения от нуля до максимального значения. Максимальное значение момента сопротивления, соответствующее началу качения, определяется равенством
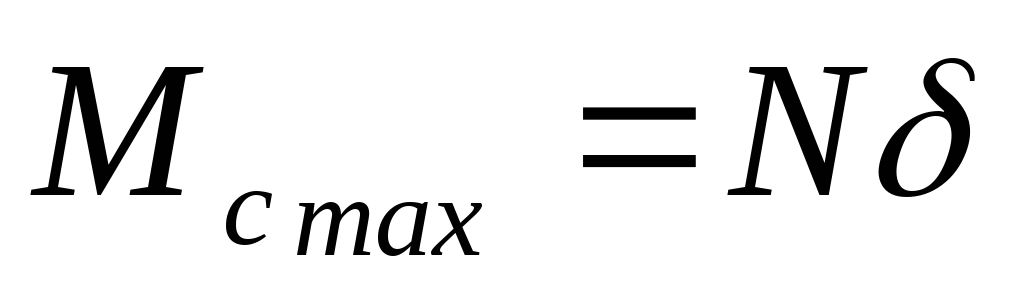 ,
,
где коэффициент трения качения (по аналогии с трением скольжения).
Коэффициент трения качения имеет размерность длины, зависит от материала контактирующих тел и геометрии зоны контакта.
Литература: [1, §18, 22, 2325, 27];
[2, §35, 36, 39];
[3, п.5.4, 5.8, 6.16.2].
1 Риттер Август (1826-1908) немецкий инженер, предложил метод расчета ферм в работе «Элементарная теория расчета железных крыш и конструкций мостов» (1862).
1 Амонтон Гийом (31.08.1663- 11.10.1705) франц. механик и физик, член Французской АН. Работы по теории трения и термометрии.
2 Кулон Шарль Огюстен (14.07.1736-13.08.1806) франц. физик, механик, инженер, член Французской АН. Исследования по строительной механике, гидравлике, теории трения, сопротивлению материалов, один из основателей электростатики.
39
nokia
1. Система сходящихся сил, действующих на твердое тело, имеет равнодействующую, которая равна геометрической сумме этих сил и проходит через точку пересечения их линий действия. 2. Для равновесия тела под действием системы сходящихся сил необходимо и достаточно, чтобы были равны нулю суммы моментов всех сил данной системы на каждую из координатных осей. 3. Укажите количество независимых уравнений равновесия при действии пространственной системы параллельных сил: 3. 4. Система двух равных по модулю параллельных сил, направленных в противоположные стороны, называется парой сил. 5. Реакция идеального стержня направлена вдоль стержня. 6. Вектор момента пары сил — это свободный вектор. 8. Укажите количество независимых уравнений равновесия при действии на тело плоской системы параллельных сил: 2. 9. Система сил, действующих на твердое тело, линии действия которых лежат в одной плоскости — это плоская система сил. 10. Реакция сферического шарнира может быть представлена тремя составляющими. 11. Одной из задач статики является установление условий равновесия тел при действии различных систем сил. 12. Алгебраическим моментом силы относительно центра называется взятое со знаком плюс или минус произведение модуля силы на плечо. 13. Силы, действующие на твердое тело и не являющиеся реакциями связей, называются активными. 14. Абсолютно твердое тело — тело, у которого расстояния между любыми двумя точками остается неизменным. 15. Сила, эквивалентная данной системе сил, называется равнодействующей. 16. Укажите количество независимых уравнений равновесия при действии на тело произвольной пространственной системы сил:6. 17. Тела, ограничивающие перемещение данного тела, называются связями. 18. Для равновесия твердого тела, находящегося под действием плоской системы сил, необходимо и достаточно, чтобы суммы проекций сил на две координатные оси и сумма моментов сил относительно произвольной точки равнялись нулю. 19. Две системы сил эквивалентны между собой, если, не нарушая состояния тела, одну систему сил можно заменить другой. 20. Плечо силы — это расстояние от центра момента до линии действия силы. 21. Момент пары сил равен моменту одной из сил пары относительно точки приложения другой силы. 22. Алгебраический момент пары сил равен алгебраическому моменту одной из сил пары относительно точки приложения другой силы или, то же самое, равен взятому со знаком плюс или минус произведению модуля одной из сил пары на плечо. 23. Силы, с которыми связи действуют на данное тело, называются реакциями связей. 24. Укажите количество независимых уравнений равновесия при действии на тело произвольной плоской системы сил: 3. 25. Реакция опорной точки перпендикулярна опирающейся поверхности. 26. Теорема о трех силах: Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. 27. Две пары, действующие на твердое тело и лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен геометрической сумме моментов составляющих пар. 28. Реакция идеальной нити направлена по нити от закрепленного тела. 29. Сумма моментов сил пары относительно произвольной точки равна моменту пары. 30. Для равновесия твердого тела под действием системы сходящихся сил, необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут. 31. Задачей статики является изучение методов преобразования систем сил в другие эквивалентные данным. 32. Реакция жесткой заделки состоит из одной силы и пары сил. Момент этой пары называется моментом заделки. 33. Моментом силы относительно оси называется алгебраическая величина, равная проекции вектора момента силы относительно произвольной точки оси на эту ось. 34. Реакция цилиндрического шарнира лежит в плоскости, перпендикулярной оси шарнира, может быть представлена двумя взаимно-перпендикулярными составляющими.
НравитсяПоказать список оценивших
Ответить

termex 21 июн 2016 в 23:32
35. Для равновесия твердого тела под действием произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор системы сил и главный момент системы сил относительно произвольно выбранного центра равнялись нулевым векторам. 36. Укажите количество независимых уравнений равновесия при действии на тело пространственной системы сходящихся сил: 3. 37. Для характеристики вращательного действия силы вводится понятие момента силы относительно центра (или точки). 38. Задача статики о равновесии системы тел называется статически определенной, если число неизвестных не превышает числа уравнений равновесия. 39. Моментом силы относительно центра называется векторное произведение радиус-вектора, проведенного из данного центра в точку приложения силы, на вектор силы. 40. Существуют ли эквивалентные формы записи уравнений равновесия твердого тела под действием плоской системы сил? Да 41. Пару сил, приложенную к твердому телу, можно перемещать в плоскости действия, сохраняя при этом ее момент. 42. Система сил, линии действия которых пересекаются в одной точке, называется сходящейся. 43. Для равновесия системы пар, действующих на твердое тело, необходимо и достаточно, чтобы сумма моментов пар равнялась нулю. 44. Пару сил, действующую на твердое тело, можно переносить в любую плоскость, параллельную плоскости ее действия. 45. Аксиомы статики — это простейшие правила эквивалентного преобразования систем сил, простейшие условия равновесия и взаимодействия тел. 46. Для равновесия твердого тела под действием пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на координатную ось, параллельную силам, и суммы моментов всех сил относительно остальных осей были равны нулю. 47. Теоремы о парах это простейшие правила эквивалетного преобразования пар и их систем. 48. Реакция гладкой поверхности направлена по нормали к этой поверхности. 49. Не изменяя действия силы на твердое тело, ее можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару сил, момент которой равен моменту данной силы относительно новой точки приложения. 50. Расстояние между линиями действия сил пары — это плечо пары сил. 51. Коэффициент пропорциональности в зависимости максимального момента сопротивления качению от нормальной реакции – это коэффициент трения качения. 52. Поверхность, образованная линией действия максимальной реакции при стремлении сдвинуть тело в различных направлениях, — это конус трения. 53. Задачей расчета ферм является определение реакций внешних связей и усилий в стержнях. 54. На практике используются различные способы нахождения центра тяжести. Один из основных — это экспериментальный метод (при подвешивании тела за любую точку его центр тяжести лежит на линии подвеса). 55. При определении усилий в стержнях фермы полагают, что стержни растнуты, направляя силы реакций от узлов. Отрицательный знак усилия, полученный в результате решения, означает, что соответствующий стержень сжат. 56. У статически определимых ферм число стержней s и число узлов n связаны соотношением: s=2n-3. 57. При повороте всех сил системы параллельных сил на один и тот же угол линия действия равнодействующей повернется в ту же сторону на тот же угол вокруг некоторой точки. Эта точка называется центром параллельных сил. 58. Ферма — это жесткая (геометрически неизменяемая) стержневая конструкция. Точка соединения стержней — узел. 59. Основными методами расчета усилий в стержнях плоских ферм являются: метод вырезания узлов и метод сечений (Риттера). 60. В результате экспериментальных исследований были установлены законы Амонтона − Кулона: 2) Максимальное значение силы трения скольжения не зависит от площади контакта, а определяется величиной нормальной реакции, материалом и состоянием контактирующих поверхностей. 61.Количество независимых уравнений равновесия при действии на ферму произвольной плоской системы сил. 3
НравитсяПоказать список оценивших
Ответить

termex 21 июн 2016 в 23:32
62.Центром тяжести твердого тела называется центр параллельных сил тяжести частиц данного тела. 63. Количество независимых уравнений равновесия узла фермы, находящегося под действием плоской системы сходящихся сил: 2 64. Сопротивление, возникающее при качении одного тела по поверхности другого, — это трение качения. 65. На практике используются различные способы нахождения центра тяжести. Один из основных — это аналитический метод (интегрирование по областям, заданным аналитическими выражениями). 66. На практике используются различные способы нахождения центра тяжести. Один из основных — это метод разбиения на части (для составных тел). 67. 1) Mmaxc=Nδ – Закон трения качения 2)Fmaxтр=fN – Закон трения скольжения 68. Коэффициент трения скольжения — коэффициент пропорциональности в зависимости максимальной силы трения от нормальной реакции при неизменном состоянии контактирующих поверхностей. 69. В результате экспериментальных исследований были установлены законы Амонтона − Кулона: 1) Сила трения скольжения при равновесии тела меняется от нуля до некоторого максимального значения. 70. Центр тяжести треугольника совпадает с точкой пересечения его медиан. 71. При стремлении сдвинуть тело, лежащее на шероховатой поверхности, возникает сила реакции, которая имеет две составляющие – нормальную и силу трения скольжения. 72. На практике используются различные способы нахождения центра тяжести. Один из основных — это метод симметрии (с учетом особенностей формы тела). 73. Одной из основных задач кинематики твердого тела является определение кинематических характеристик отдельных точек тела. 74. Кинематическая мера движения точки, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета — это скорость точки. 75. Движение твердого тела, при котором любая прямая, связанная с телом, остается параллельным своему начальному положению — это поступательное движение. 76. Скорость точки − это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. 77. Кинематическая мера движения точки, равная производной по времени от скорости этой точки в рассматриваемой системе отсчета — это ускорение точки. 78. Одной из основных задач кинематики твердого тела является описание способов задания движения твердого тела. 79. Кинематическая мера движения точки, равная второй производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета — это ускорение точки. 80. Задачей кинематики является определение кинематических характеристик движения точки (скорости, ускорения) по заданному закону движения. 81. Нормальное ускорение точки — это проекция вектора ее ускорения на главную нормаль к траектории движения. 82. Ускорение точки характеризует изменение вектора скорости по величине и направлению. 83. Изменение скорости точки по величине характеризует касательное ускорение. 84. При естественном способе задания движения задаются: траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты. 85. Вектор углового ускорения − это производная вектора угловой скорости по времени. 86. Вращательным называется движение твердого тела, имеющего две неподвижные точки. Прямая, проходящая через эти точки — это ось вращения. 87. Нормальное ускорение точки определяется отношением квадрата ее скорости к радиусу кривизны траектории. 88. Механическое движение − это изменение положения одного тела относительно другого (тела отсчета), с которым связана система координат. 89. Алгебраическое значение касательного ускорения точки — это проекция вектора ускорения на касательную к траектории движения точки. 90. При естественном способе задания движения точки ее касательное ускорение определяется второй производной от дуговой координаты по времени.
НравитсяПоказать список оценивших
Ответить

termex 21 июн 2016 в 23:33
91. Нормальное ускорение точки характеризует изменение ее скорости по направлению. 92. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы. 93. Одной из основных задач кинематики точки является описание способов задания движения точки. 94. Одной из основных задач кинематики твердого тела является определение кинематических характеристик движения твердого тела. 95. Геометрическое место последовательных положений движущейся точки в рассматриваемой системе отсчета − это траектория точки. 96. При векторном способе задания движения точки ее положение определяется радиус-вектором, проведенным из неподвижной точки, связанной с телом отсчета. 97. Алгебраическая скорость − проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. 98. Кинематическая мера изменения скорости — ускорение точки. 99. Естественные оси (касательная, главная нормаль, бинормаль) − это оси подвижной прямоугольной системы координат с началом в движущейся точке. Их положение определяется траекторией движения. 100. Система координат, в которой рассматривается движение точки, и тело отсчета называются системой отсчета. 101. При координатном способе задания движения задаются координаты точки как функции времени. 102. Вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости – это вектор угловой скорости. 103. Движение точки (или тела) по отношению к подвижной системе отсчета — относительное движение. 104. v⃗ =v⃗r+v⃗ e — теорема сложения скоростей a⃗ =a⃗ r+a⃗ e+a⃗ c, a⃗ c=2ω⃗ e×v⃗ r – Теорема Кориолиса 104. Теорема о сложении скоростей: При сложном движении точки абсолютная скорость равна сумме ее относительной и переносной скоростей. 105. Переносное ускорение точки − это ускорение того места подвижной системы координат, с которым в данный момент совпадает движущаяся точка. 106. Угловая скорость тела при его плоском движении, скорость его произвольной точки A и расстояние от этой точки до мгновенного центра скоростей P связаны соотношением: ω=vAAP Да 107. Способы вычисления ускорения Кориолиса: 1. По правилу вычисления векторного произведения. 2. По правилу Жуковского. 108. Движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости – это плоское (или плоско-параллельное) движение твердого тела. 109. Скорость того места подвижной системы координат, с которым в данный момент совпадает движущаяся точка — это переносная скорость. 110. Движение подвижной системы отсчета относительно основной — переносное движение. 112. Движение плоской фигуры можно рассматривать как сложное, которое складывается из относительного и переносного. Поступательное движение подвижной системы координат вместе с произвольной точкой, жестко связанной с фигурой, называемой полюсом – это переносное движение. 113. Зависит ли закон изменения угла от выбора полюса? Не зависит 114. Зависит ли угловая скорость твердого тела, совершающего плоское движение, от выбора полюса? Не зависти 115. Правило Жуковского: Для определения направления ускорения Кориолиса надо вектор относительной скорости спроецировать на плоскость, перпендикулярную оси вращения в переносном движении, и повернуть в сторону вращения на угол 90 град. 116. Модуль ускорения Кориолиса: ac=2∣ω⃗ e∣∣v⃗ r∣sinα Верно 117. Скорость любой точки плоской фигуры находится как скорость во вращательном движении вокруг мгновенного центра скоростей. 118. Абсолютное ускорение точки − это ускорение точки в основной системе отсчета. 119. Движение точки (или тела) по отношению к основной системе отсчета — абсолютное движение.
НравитсяПоказать список оценивших
Ответить

termex 21 июн 2016 в 23:33
120. Эти уравнения определяют движение плоской фигуры: xA=xA(t), yA=yA(t), φ=φ(t) Да 121. Теорема Кориолиса: При непоступательном переносном движении абсолютное ускорение точки находится как сумма трех ускорений: относительного, переносного и ускорения Кориолиса. 122. Движение плоской фигуры можно рассматривать как сложное, которое складывается из относительного и переносного. Вращение плоской фигуры вокруг выбранного полюса — это плоское движение. 123. Абсолютная скорость точки − это скорость точки в основной системе отсчета. 124. Относительное ускорение точки — это ускорение точки в подвижной системе отсчета. 125. Движение точки (или тела), которое рассматривается одновременно в разных системах отсчета, — это сложное движение. 126. Теорема. Скорость любой точки тела при плоском движении находится как сумма скорости полюса и скорости данной точки во вращательном движении вокруг полюса. 127. v⃗ ,a⃗ — Кинематические характеристики абсолютного движения v⃗ e,a⃗ e — Кинематические характеристики переносного движения v⃗ r,a⃗ r — Кинематические характеристики относительного движения 128. При задании плоского движения за полюс может приниматься любая точка тела. 129. Относительная скорость точки — это скорость точки в подвижной системе отсчета. 130. Ускорение Кориолиса учитывает изменение относительной скорости, вызванное переносным движением, и изменение переносной скорости, вызванное относительным движением. 131. Теорема. При непоступательном движении плоской фигуры существует жестко связанная с ней точка, скорость которой в данный момент движения равна нулю. Эта точка является мгновенным центром скоростей.
термех












7.Фермой называется жесткая (геометрически неизменяемая) конструкция из прямолинейных стержней, соединенных на концах шарнирами.
Ферма считается статически определимой, если число узлов n и число стержней m удовлетворяют уравнению:
m=2n-3 если число стержней не удовлетворяет этому равенству, то возможны два случая:
1. если: m>2n-3,
ферма является в этом случае статически неопределимой;
2. если: m<2n-3,
то конструкция перестает быть геометрически неизменяемой. Получает подвижность, следовательно, становится механизмом.
Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях. Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело. Расчет усилий в стержнях фермы методами статики может быть произведен только для статически определимых ферм.
Метод вырезания узлов.
Этим
методом удобно пользоваться, когда надо
найти усилия во всех стержнях фермы. Он
сводится к последовательному рассмотрению
условий равновесия сил, сходящихся в
каждом из узлов, определению усилий в
стержнях фермы.
Активные
силы и реакции опор являются внешними
силами для всей фермы, рассматриваемой
как твердое тело; усилия в стержнях в
этом случае -внутренние силы. Поэтому
для определения усилий необходимо
рассмотреть равновесие части фермы,
для которой искомые усилия являются
внешними силами.
При
решении задач на расчете ферм способом
вырезания узлов необходимо придерживаться
следующего плана действий:
1. Выбор
тела (или т ел),равновесие которого
должно быть рассмотрено. Для решения
задачи надо рассмотреть равновесие
тела, к которому приложены заданные и
искомые силы или силы, равные искомым
(например, если надо найти давление на
опору, то можно рассмотреть равновесие
тела, к которому приложена численно
равная этой силе реакция опоры и т. п.). 2. Когда
заданные силы действуют на одно тело,
а искомые на другое или когда те и другие
силы действуют одновременно на несколько
тел, может оказаться необходимым
рассмотреть равновесие системы этих
тел или последовательно равновесие
каждого тела в отдельности.
3. Изображение
действующих (активных) сил. Установив
равновесие какого тела или тел
рассматривается (и только после этого),
следует на чертеже изобразить все
действующие на это тело, (или тела)
внешние силы, включая как заданные, таи
и искомые сковы, в том числе реакции
всех связей.
4. Составление
условий равновесия. Условия равновесия
составляют для сил, действующих на тело
(или тела), равновесие которых
рассматривается.
5. Определение
,реакции опор, пользуясь уравнениями
равновесия для всей фермы, рассматриваемой
как твердое тело, проверка правильности
решения и исследование полученных
результатов.
6. Вырезать
узел, в котором сходятся два стержня, и
рассмотреть его равновесие под действием
активных сил и реакций разрезанных
стержней; определить эти реакции
7. Переходя
от узла к узлу, рассматривать аналогично
равновесие каждого узла. 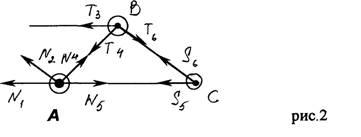
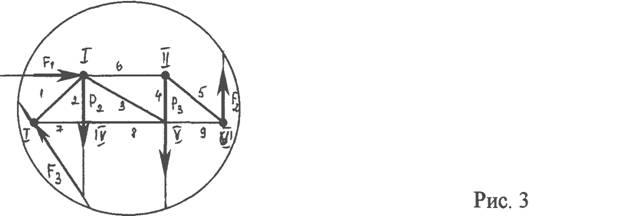
Определение усилий в стержнях фермы построением диаграммы Максвелла-Кремоны. Это графический способ расчета усилий в стержнях фермы. Построение диаграммы Максвелла-Кремоны заключается в построении силовых многоугольников, построенных для всех узлов фермы, в один чертеж так, чтобы ни одно из усилий не повторялось дважды (рис. 3). При расчете фермы способом Максвелла-Кремоны следует придерживаться следующей последовательности действий: 1.Определить реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматриваемой как твердое тело. 2.Отбросить опоры и изобразить все приложенные к ферме внешние силы, включая реакции опор, так чтобы эти векторы располагались вне контура фермы. 3.Части плоскости, ограниченные контуром фермы и линиями действия внешних сил, а так же те, что ограниченны стержнями фермы, обозначить буквами; узлы обозначить римскими цифрами, стержни — нумеруем арабскими. 4.Построить замкнутый многоугольник внешних сил, откладывая силы в том порядке, в котором они встречаются при обходе фермы (направление произвольно) силы обозначаются малыми буквами, соответствующими обозначениям смежных участков плоскости. 5.Последовательно, на том же рисунке, построить силовые многоугольники для каждого узла (узлы выбираются таким образом, чтобы число неизвестных усилий в стержнях равнялось двум), направление обхода узла должно совпадать с направлением обхода плоскости. 6.Стержень считать сжатым, если направление, указанное известными силами, направлено к узлу, в противном случае стержень растянут 7.Измерить на диаграмме отрезки, изображающие искомые усилия в стержнях фермы, и найти усилия, учитывая принятый масштаб сил.

Определение усилий в стержнях фермы методом сечений (методом Риттера).
Этим
методом удобно пользоваться для
определения усилий в отдельных стержнях
фермы, например, для проверочных расчетов
(рис. 4)
При
расчете методом сечении рекомендуется
такая последовательность
действии:
1. Определить
реакции опор, пользуясь уравнениями
равновесия для всей фермы, рассматриваемой
как твердое тело, находящееся под
действием плоской системы сил.
2. Ферму
разделяют на две части сечением,
проходящим через три стержня, в которых
(или в одном из которых) требуется
определить усилия, и рассматривают
равновесие одной из этих частей. Действие
отброшенной части заменяют соответствующими
силами, направляя их вдоль разрезанных
стержней от узлов, т. е., считая их
растянутыми.
3. Затем
составляются уравнения равновесия так,
чтобы в каждое уравнение входило одно
неизвестное усилие. 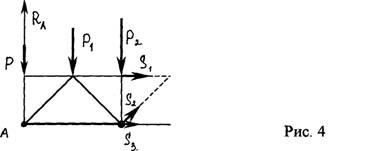 Из
полученных уравнений находятся
неизвестные усилия в стержнях; если в
ответе получается знак «-», то это
означает, что стержень сжат, а не
растянут.
Из
полученных уравнений находятся
неизвестные усилия в стержнях; если в
ответе получается знак «-», то это
означает, что стержень сжат, а не
растянут. 







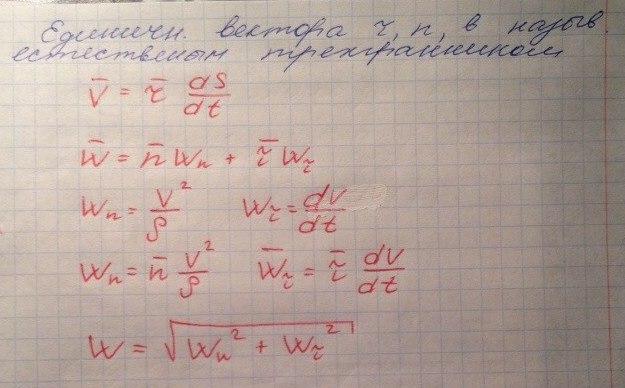


13.
Вычисление скорости и ускорения любой точки тела, вращающегося вокруг неподвижной оси.
(необязательная часть ответа, просто пара описаний вращательного движения)
Вращательным
движением твердого тела вокруг неподвижной
оси называется такое движение, при
котором какие-нибудь 2 точки, принадлежащие
телу, остаются неподвижными. Проходящая
через эти точки прямая называется осью
вращения. Для того, чтобы задать
вращательное движение берут две плоскости
проходящие через ось вращения. Одна из
них –неподвижная плоскость, другая –
скреплена с телом. Угол поворота 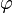 позволяет однозначно определить
положение любой точки в нужный момент
времени. задать движение можно задавая
угол поворота.
позволяет однозначно определить
положение любой точки в нужный момент
времени. задать движение можно задавая
угол поворота.
(ответ)
Вращение
характеризуется углом 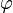 ,
измеряющимся в градусах или радианах, угловой
скоростью
,
измеряющимся в градусах или радианах, угловой
скоростью 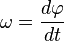 (измеряется
в рад/с) – показывающей быстроту изменения
угла поворота, и угловым
ускорением
(измеряется
в рад/с) – показывающей быстроту изменения
угла поворота, и угловым
ускорением 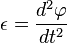 (единица
измерения — рад/с²)-показывающим
быстроту изменения угловой скорости.
(единица
измерения — рад/с²)-показывающим
быстроту изменения угловой скорости.
Буквами греческого алфавита (сигма, омега, эпсилон) обозначаются характеристики движения тела в целом. Буквами латинского алфавита V,W,S,Y,Z характеризуется движение точки. Вектор ω при вращательном движении всегда направлен по оси вращения так, чтобы глядя на встречу этому вектору мы видели вращение тела против хода часовой стрелки. Вектор ε направлен также как и ω при ускоренном движении и в противоположную сторону в замедленном.
Скорость точки:
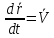

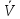 =
=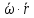
V=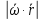 =
=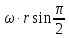 =
=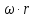
Ускорение точки:
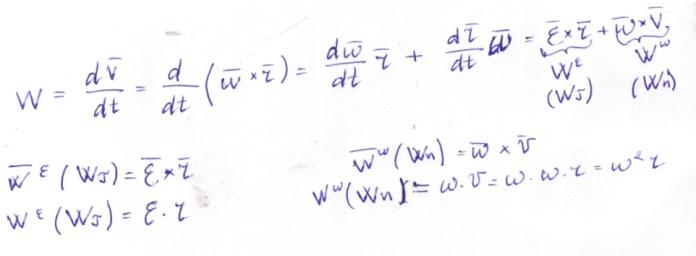
14. Плоскопараллельное движение твердого тела. Законы движения.
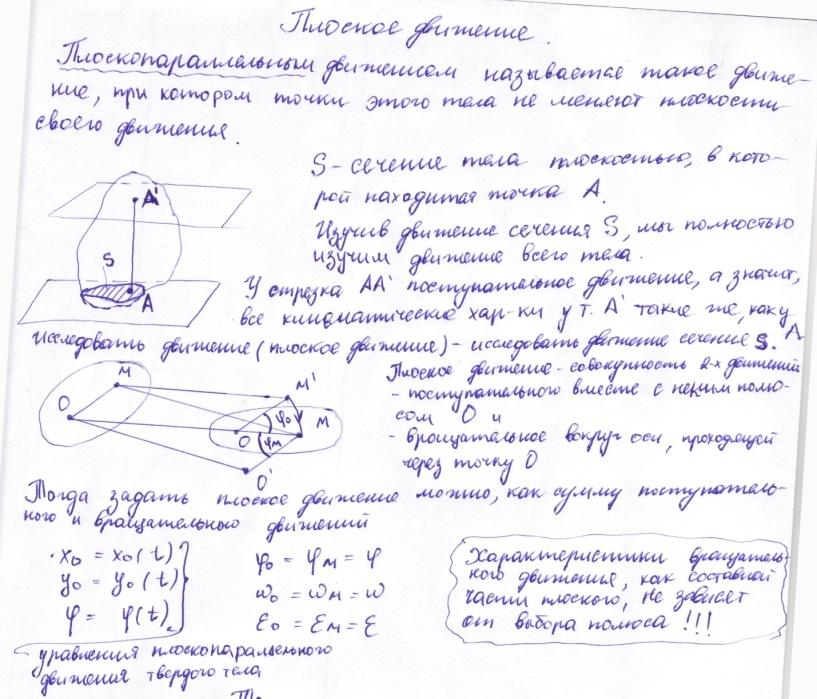
Плоскопараллельным называется такое движение тела, при котором точки этого тела не меняют плоскости своего движения.
Изучив движение плоскости S мы полностью изучим движение всего тела. Плоское движение можно представить как совокупность поступательного и вращательного движений. Чтобы задать положение плоской фигуры а значит и всего тела необходимо задать положение точки А, а также задать вращение плоской фигуры.
15.Способы вычисления скорости точки плоской фигуры в данный момент времени.


16.Способы вычисления ускорения точки плоской фигуры в данный момент времени.
























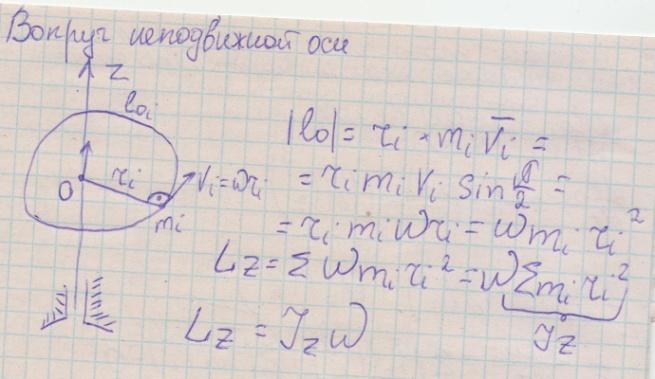



















Расчётно-графическая работа №1.
Часть 1. Определение реакций опор и усилий в стержнях плоской фермы.
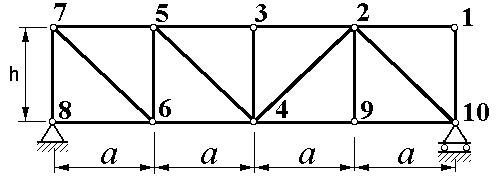
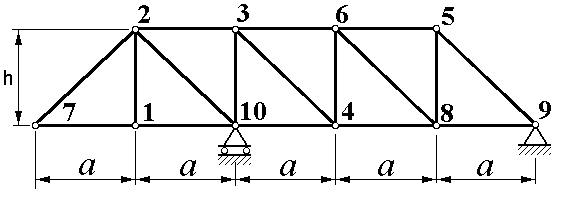
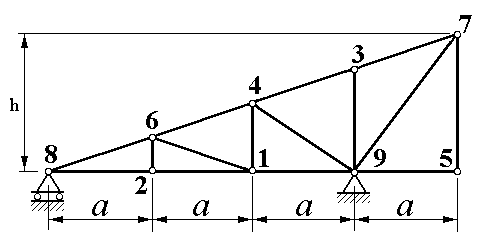
Расчётная схема плоской фермы, образованная шарнирным соединением стержней в форме треугольников, изображена на рисунках 1.0-1.9. Цифрами на схемах пронумерованы узлы фермы (точки, в которых сходятся оси стержней). Ферма закреплена на двух шарнирах (один – подвижный, другой — неподвижный) или на неподвижном шарнире и невесомом стержне.
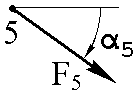
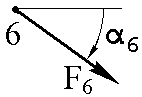
На ферму действуют три внешние силы, приложенные в узлах фермы. Номера узлов, где приложены силы и направление действия сил указаны в таблице 1.1. Геометрические размеры фермы и величины внешних сил указаны в таблице 1.2.
Нумерация рисунков и таблиц в РГР №1 выполнена двумя цифрами, разделёнными точкой. Первая цифра указывает на принадлежность рисунка (таблицы) к первой или ко второй части. Номером рисунка (таблицы) является вторая цифра, стоящая после точки. Например, рисунок 1.3 – это рисунок №3 в первой части работы.
Выбор варианта задания студент осуществляет по своему шифру, образованному тремя последними цифрами номера зачётной книжки. Например, если номер зачётной книжки 261573, то шифр студента будет «573». По третьей (последней) цифре шифра выбирается номер рисунка, по второй (средней) цифре шифра выбирается номер условия (строки) в таблице 1.1; по первой цифре шифра – номер условия (строки) в таблице 1.2.
В каждом варианте заданий требуется определить:
реакции опор фермы,
усилия в стержнях фермы.
Таблица 1.1 | ||||||
Номер условия | Номер узла и направление действия силы | |||||
| | | | | ||
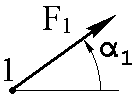
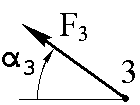
α1, град. | α2, град. | α3, град. | α4, град. | α5, град. | α6, град. | |
0 | 30 | — | 45 | — | 60 | — |
1 | — | 30 | — | 45 | — | 60 |
2 | 45 | — | 60 | — | 30 | — |
3 | — | 45 | — | 60 | — | 30 |
4 | 60 | — | 30 | — | 45 | — |
5 | — | 60 | — | 30 | — | 45 |
6 | 75 | — | 60 | — | 15 | — |
7 | — | 60 | — | 15 | — | 75 |
8 | 60 | — | 15 | — | 75 | — |
9 | — | 15 | — | 75 | — | 60 |
Таблица 1.2 | ||||||||
Номер условия | Размеры, м | Силы, кН | ||||||
a | h | F1 | F2 | F3 | F4 | F5 | F6 | |
0 | 4 | 3 | 10 | 15 | 20 | 25 | 30 | 20 |
1 | 3 | 4 | 15 | 20 | 25 | 30 | 20 | 25 |
2 | 4 | 2 | 20 | 25 | 30 | 20 | 10 | 20 |
3 | 3 | 6 | 25 | 30 | 35 | 25 | 30 | 15 |
4 | 2 | 2 | 30 | 25 | 10 | 15 | 20 | 25 |
5 | 4 | 6 | 25 | 15 | 15 | 20 | 20 | 10 |
6 | 3 | 2 | 15 | 20 | 25 | 15 | 35 | 20 |
7 | 3 | 3 | 20 | 25 | 20 | 20 | 30 | 15 |
8 | 5 | 3 | 25 | 15 | 30 | 25 | 15 | 20 |
9 | 5 | 4 | 30 | 20 | 15 | 30 | 20 | 15 |
Таблица 1.3
N стержня
1-2
2-3
3-4
4-5
5-6
6-7
7-8
Усилие S, кН
–15,8
–25,8
–25,8
0
0
24,2
24,3
N стержня
1-8
2-8
3-8
4-8
6-4
7-4
Усилие S, кН
–7,3
22,3
0
–22,3
–34,2
30

Рисунок 1.0

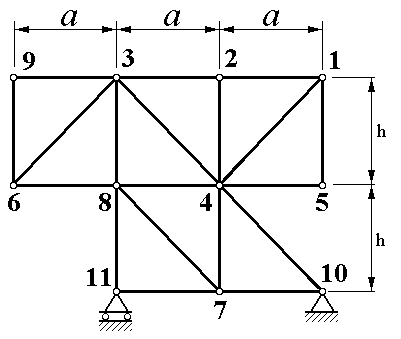
Рисунок 1.1

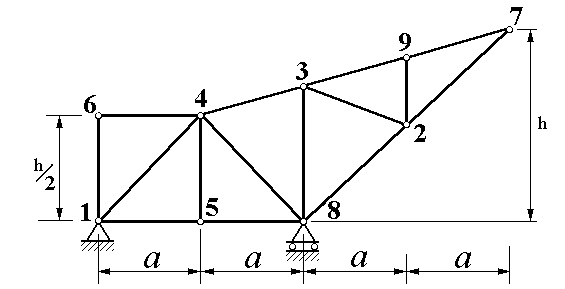
Рисунок 1.2

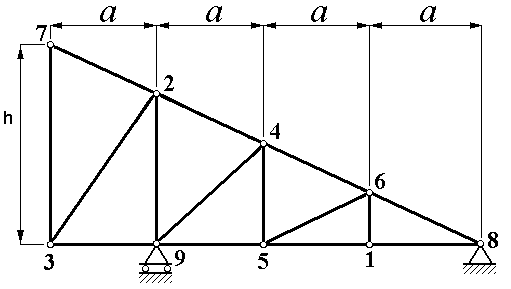
Рисунок 1.3

Рисунок 1.4

Рисунок 1.5

Рисунок 1.6

Рисунок 1.7

Рисунок 1.8

Рисунок 1.9
Указания. Задача первой части на равновесие тела, находящегося под действием произвольной плоской системы сил.
Определение реакции опор рекомендуется выполнить в следующей последовательности. Нарисовать схему фермы, расставить заданные внешние силы, выбрать направление координатных осей, вычислить проекции заданных сил на координатные оси и нанести проекции сил на схему с указанием направления их действия. Значения заданных сил и рассчитанные значения проекций сил целесообразно выписать в табличной форме вблизи схемы фермы, что позволит проверить правильность разложения сил и облегчит использование полученных значений при составлении и решении уравнений равновесия.
Далее необходимо отбросить связи фермы (опорные шарниры и стержень), заменив их соответствующими реакциями. При отбрасывании неподвижного шарнира в состав действующих сил вводятся две составляющих реакции опоры – по оси Х и по оси У.
При отбрасывании подвижного шарнира или стержня вводится по одной реакции: вместо шарнира – перпендикулярно опорной поверхности, вместо стержня – по направлению стержня.
В каждом варианте задания должно быть по три неизвестных реакции, которые подлежат определению из трёх уравнений равновесия. Составлять и решать уравнения равновесия можно в любой последовательности. Однако наиболее рационально начать с уравнения суммы моментов всех сил относительно точки неподвижного шарнира, где две неизвестных реакции, которые не войдут в это уравнение. Затем можно решать уравнения сумм проекций всех сил на координатные оси.
После определения всех трёх реакций необходимо выполнить проверку. Для этого нужно составить и решить уравнение моментов относительно любого узла фермы, через который не проходят линии действия реакций опор.
Определение усилий в стержнях нужно выполнять с использованием двух способов – «вырезанием» узлов и методом сечений.
Однако, прежде чем приступить к расчётам, следует выявить наличие стержней, усилия в которых равны нулю («нулевые стержни»), пользуясь следующими леммами:
Лемма 1. Если в незагруженном узле плоской фермы сходятся два стержня, то усилия в этих стержнях равны нулю.
Лемма 2. Если в незагруженном узле плоской фермы сходятся три стержня, из которых два расположены на одной прямой, то усилие в третьем стержне равно нулю. Усилия в первых двух стержнях равны между собой.
Лемма 3. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне по модулю равно приложенной силе, а усилие в другом стержне равно нулю.
Усилие в стержне обозначается буквой S, а номер стержня определяется номерами узлов, между которыми расположен стержень. Так, стержень «4-5» соединяет узел 4 с узлом 5.
Определение усилия в стержнях фермы по методу вырезания узлов сводится к последовательному рассмотрению равновесия отдельных узлов фермы под действием сил, сходящихся в этом узле. Действие отброшенной части фермы заменяется действием реакций перерезанных стержней, численно равных искомым усилиям в стержнях. Эти усилия направляются вдоль стержней от узла, предполагая стержни растянутыми. Если в результате расчёта усилие в стержне окажется со знаком «минус», это означает, что стержень не растянут, а сжат.
Вырезание следует начинать с узла, в котором сходятся два стержня, так как при рассмотрении его равновесия можно составить только два уравнения:
как для плоской системы сходящихся сил. При вырезании последующих узлов необходимо следить, чтобы в каждом из них было не более двух стержней с неизвестными усилиями.
К вырезанному узлу прикладывается заданная внешняя сила или определённая ранее опорная реакция. Определение неизвестных усилий можно выполнять аналитическим или графическим методами.
При аналитическом методе для узла выбирается система координат (ХУ) и составляются два уравнения равновесия – суммы проекций всех сил на координатные оси, из которых определяются неизвестные усилия.
При графическом методе решения для сходящейся системы сил вырезанного узла строится многоугольник, который должен быть замкнутым из условия равновесия. Для построения многоугольника сил выбирается масштаб (в 1 см – 5 кН или 10 кН) и произвольная точка. Из этой точки в выбранном масштабе откладываются последовательно вектора известных сил, параллельно линиям их действия, так чтобы последующий вектор пристраивался в конец предыдущего. Затем через начальную точку построения и через конец последнего вектора проводятся по две линии параллельно неизвестным усилиям. Точка пересечения линий действия неизвестных усилий позволяет построить замкнутый многоугольник, из которого находится длина отрезков, соответствующих неизвестным усилиям и направление действия усилий. Длина отрезков с помощью масштаба пересчитывается в величину силы. Направление усилий должно быть таким, чтобы стрелки всех векторов в многоугольнике были ориентированы по контуру в одну сторону.
Графическим методом следует определить усилия как минимум в двух узлах фермы.
При аналитическом решении уравнений равновесия и при графическом решении (построением многоугольника) необходимо руководствоваться следующими правилами знаков:
При составлении расчётной схемы каждого последующего узла найденные ранее усилия в стержнях независимо от их знака направляются от узла.
При вычислениях определённые ранее усилия берутся с учётом знака.
При подстановке усилия из одного уравнения в другое знак «минус» учитывается.
При построении силовых многоугольников найденные ранее усилия в стержнях откладываются с учётом знака: если положительное, то направляется от узла, если отрицательное – к узлу.
Для определения усилий во всех стержнях фермы достаточно решить уравнения равновесия для (N-1) узлов.
Проверка правильности определения усилий производится при вырезании последнего узла. Если усилия определены правильно, то уравнения равновесия сил последнего узла должны обратиться в тождество типа 0=0.
Определение усилий в стержнях методом сечений (способ Риттера). Для этого:
а) «разрезаем» мысленно ферму на две части так, чтобы отсекалось не менее двух узлов и оказались «перерезанными» три стержня, усилия в которых (или в одном из которых) нужно определить.
б) рассматриваем равновесие одной из частей фермы, причём действие отброшенной части заменяем действием реакций перерезанных стержней, численно равных искомым усилиям. Эти усилия направляем вдоль перерезанных стержней от узлов, то есть предполагаем стержни растянутыми.
в) составляем уравнения равновесия для выделенной части фермы таким образом, чтобы в каждое уравнение вошло только одно усилие в стержне, которое в данном случае мы хотим определить. Обычно это уравнения моментов всех сил относительно точек, где пересекаются действия двух других неизвестных усилий, или уравнения проекций на ось, перпендикулярную двум другим неизвестным усилиям.
Метод сечений необходимо использовать хотя бы один раз для определения неизвестных усилий в стержнях или для проверки усилий, определённых методом вырезания узлов, – по усмотрению студента.
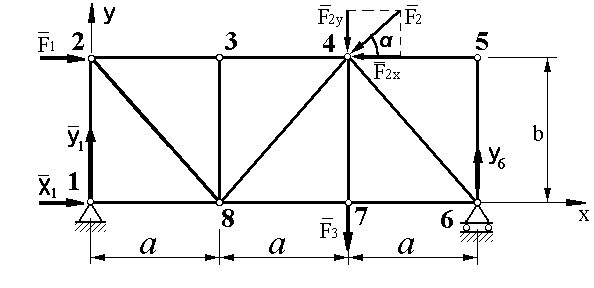
Пример. Плоская ферма (рисунок 1.10) прикреплена в узле 1 к неподвижному шарниру, а в узле 6 – к подвижному. Действующие на ферму три внешние силы и размеры фермы указаны на рисунке.
Дано:
F1=10
кН; F2=20
кН,  =30º;
F3=30
кН; a=2
м; b=2
м.
=30º;
F3=30
кН; a=2
м; b=2
м.
Определить опорные реакции и усилия во всех стержнях фермы.

Рисунок 1.10
Решение.
Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков)
80
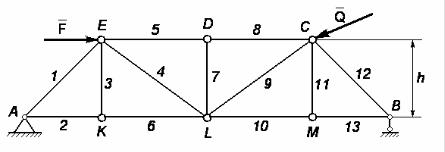
Стержни 3, 7, 11 – называются стойками. Стержни 1, 4, 9, 12 – называются раскосами.
Стержни, образующие замкнутый треугольник, называют панелью фермы.
Рис. 56
Ферма на рис. 56 имеет 6 панелей.
При расчете фермы принимают следующие допущения.
1.Все стержни фермы прямолинейные и невесомые.
2.Узлы фермы — идеальные шарниры.
3.Внешние силы приложены к узлам фермы.
4.Стержни фермы воспринимают только продольные усилия: сжатие или растяжение.
Расчет фермы состоит в определении опорных реакций и внутренних усилий в стержнях фермы.
При расчете опорных реакций ферма рассматривается как твердое тело, на которое действует плоская система сил. Расчет заключается в составлении расчетной схемы, составлении уравнений равновесия и определении неизвестных реакций.
Усилия в стержнях фермы определяются:
1.Методом вырезания узлов.
2.Методом сечений (методом Риттера).
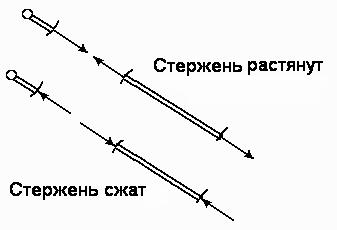
При составлении расчетных схем следует иметь в виду, что если стержень растянут, то сила, с которой он действует на узел, направлена от узла к стержню. Если же стержень сжат, то усилие направлено к узлу от стержня (рис. 57).
81
Рис. 57
Метод вырезания узлов
Метод вырезания узлов состоит в последовательном вырезании узлов фермы и рассмотрении их равновесия. Так как на узел действует плоская сходящаяся система сил, для которой можно записать только два уравнения равновесия, то вырезать узлы надо так, чтобы неизвестных сил было не больше двух. При составлении расчетной схемы будем считать, что все стержни растянуты, т.е. все внутренние усилия направим от узла к стержню. Для каждого узла составляются уравнения равновесия
n
∑Fkx = 0, k =1
n
∑Fky = 0. k =1
Если усилия в стержнях, найденные по этим формулам, имеют знак « + », то формально это указывает на то, что стержень растянут, если же знак усилия « – », то стержень сжат.
Метод сечений
Метод сечений (метод Риттера) заключается в том, что ферма рассекается на две части. Одна часть фермы отбрасывается, а ее действие отображается усилиями в стержнях оставшейся части, которые попали в сечение. Усилия в стержнях направляются вдоль

82
стержней к отброшенной части фермы, т.е. опять предполагаем, что все стержни растянуты. Рассматриваемая часть фермы, на которую действуют активные (заданные) силы, опорные реакции и усилия в стержнях, находится в равновесии. При этом получается произвольная плоская (не сходящаяся) система сил, для которой можно записать три уравнения равновесия. Поэтому неизвестных сил в сечении не должно быть больше трех.
Как известно, существуют три формы уравнений равновесия для плоской системы:
n
∑Fkx = 0;
k=1
n
∑Fky = 0;
k=1
n
∑Mo(Fk ) = 0.
k=1
1-я форма
n
∑Fkx = 0;
k=1
n
∑MA (Fk ) = 0.
k=1
n
∑MB(Fk ) = 0.
k=1
2-я форма
n
∑MA (Fk ) = 0.
k=1
n
∑MB(Fk ) = 0.
k=1
n
∑MC(Fk ) = 0.
k=1
3-я форма
При составлении уравнений равновесия выбирается та форма, которая позволяет получить наиболее простые уравнения. Например, если в сечении две неизвестные силы параллельны, то удобно применить 2-ю форму уравнений. Если все силы в сечении попарно пересекаются, то 3-ю форму. В этом случае точки пересечения сил выбираются в качестве моментных точек. Полученное таким образом каждое уравнение равновесия будет содержать одну неизвестную. По сравнению с методом вырезания узлов это значительно ускоряет расчет и увеличивает точность вычислений.
Если в сечении оказывается больше трех неизвестных усилий, то приходится проводить дополнительные сечения.
83
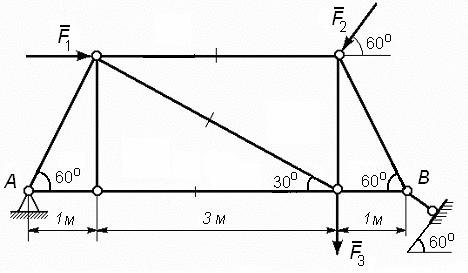
Пример решения задачи
На ферму, показанную на рис. 58, действуют силы F1 = 1 кН, F2 = 2 кН и F3 = 3 кН.
Рис. 58
Определить реакции опор, усилия в стержнях фермы методом вырезания узлов. Для отмеченных стержней проверить усилия методом сечений.
Решение
Обозначим все узлы буквами, а стержни цифрами. Отбросим все опоры и заменим их действие опорными реакциями N1, N2 и NB.
Покажем координатные оси. Полученная расчетная схема представлена на рис. 59.
Проверим ферму на статическую определимость. Ферма имеет 6 узлов и 9 стержней, т.е. У = 6, С = 9. Подставив эти значения в формулу С = 2У – 3, получаем тождество 9 = 2•6 – 3 = 9. Ферма статически определимая.
Для определения опорных реакций воспользуемся первой формой уравнения равновесия для плоской системы сил.
∑Fkx = N1 + F1 − F2 cos600 −NB cos300 = 0;
84
∑Fky = N2 − F2 sin60o −F3 −NB sin30o = 0;
∑MA(Fk ) = −F1 1 tg60o + F2 cos60o 1 tg60o − F2 sin60o 4 − −F3 4 − NB sin30o 5 = 0.
|
|
| Рис. 59 |
|
Из последнего уравнения находим |
| |||
N = |
| 1 | (F 1 tg60o − F cos60o 1 tg60o + | |
|
| |||
B | 5 | sin300 | 1 | 2 |
|
|
| ||
+F3 4) = 0,4 (1,732 −1,732 + 6,928 +12) =
=0,4 18,928 =7,571 кН.
Подставив это значение в первые два уравнения, находим
N1 = −F1 + F2 cos60o + NB cos30o = −1+ 2 0,5 + 7,571 0,866 = = −1+1+ 6,557 = 6,557кН,
85
N2 = +F2 sin60o + F3 − NB sin30o = 2 0,866 + 3 − 7,571 0,5 = =1,732 + 3 − 3,785 = 0,947 кН.
Итак, N1 = 6, 557 кН, N2 = 0,947 кН, NB = 7,571 кН.
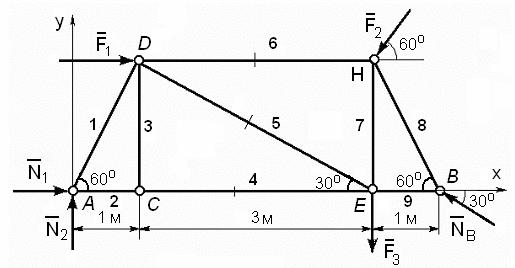
Теперь определим усилия в стержнях фермы методом вырезания узлов. Начинать вырезание можно с узла A или узла B, так как в них неизвестны усилия только в двух стержнях. Начнем с узла A. Вырежем узел A и рассмотрим его равновесие. На узел действует сходящаяся система сил: реакции опор N1 и N2, а также усилия в стержне 1 – S1 и в стержне 2 — S2 . Усилия в стержнях направляем от узла в сторону соответствующих стержней, т.е. мы предполагаем, что эти стержни растянуты. В точке A поместим начало прямоугольной координатной системы Axy. Расчетная схема для узла A показана на рис. 60.
Узел A
Рис. 60
Вэтом случае уравнения равновесия имеют вид
∑Fkx = N1 +S1 cos60о +S2 = 0;
∑Fky = N2 + S1 sin60о = 0.
Из второго уравнения находим

86
S1 = − sinN602 O = − 0,9470,866 = −1,093кН .
Из первого уравнения находим
S2 = −N1 −S1 cos60O = −6,557 −(−1,093) 0,5 = −6,01кН.
Знак « – » формально указывает, что оба стержня сжаты.
Так как усилие в стержне 2 найдено, то можно переходить к узлу C. В этом случае неизвестны усилия в стержнях 3, 4 – S3, S4.
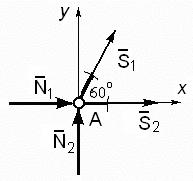
Вырежем узел C и составим для него расчетную схему также, как это было сделано для узла A (рис. 61).
Узел C
Рис. 61
Уравнения равновесия имеют вид
∑Fkx = −S2′ + S4 = 0,
∑Fky = S3 = 0.
Так как S2\ = S2 = –6,01кН, то из уравнений находим
S4 = S2′ = −6,01кН, S3 = 0.
Следовательно, стержень 4 сжат, а в стержне 3 усилия нет. Вырежем узел D. Расчетная схема для него показана на рис. 62.
Неизвестными здесь являются усилия в стержнях 5 и 6 – S5 , S6.
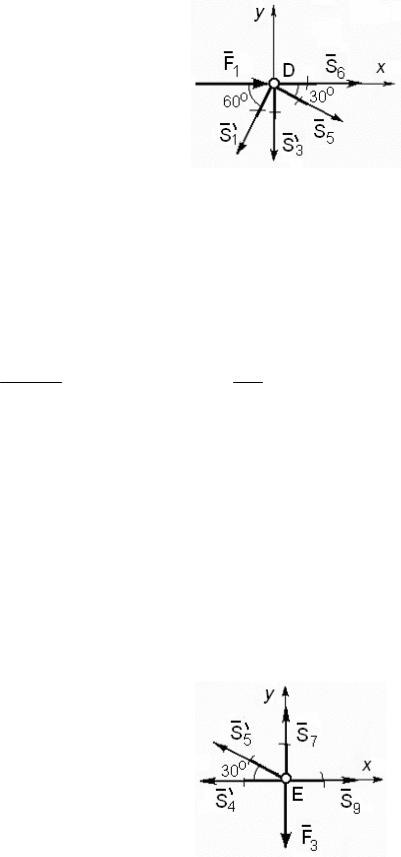
87
Узел D
Рис. 62
Уравнения равновесия имеют вид
∑Fkx = F1 −S1′cos600 + S5 cos300 + S6 = 0,
∑Fky = −S1′sin600 −S3′ −S5 sin300 = 0.
Так как S1\ = S1 = –1,093кН, S3\ = S3 = 0, то из уравнений находим
S5 = sin301 0 (−S1′sin600 −S3′ )= 0,51 −(−1,093) 0,866 − 0 =1,893кН, S6 = −F1 + S1′cos600 −S5 cos300 =
=−1+(−1,093) 0,5 −1,893 0,866 = −3,186кН.
Стержень 5 растянут, стержень 6 сжат.
Так как усилия в стержнях 4, 5 и 6 найдены, то можно переходить
кузлу E или H.
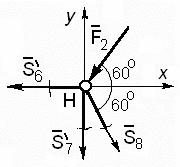
Вырежем узел E. Расчетная схема для него показана на рис. 63. Неизвестными здесь являются усилия в стержнях 7 и 9 – S7, S9.
Узел E
88
Уравнения равновесия имеют вид
∑Fkx = −S4′ −S5′ cos300 + S9 = 0,
∑Fky =S5′ sin300 + S7 − F3 = 0.
Так как S’4 = S4 = –6,01 кН и S’5 = S5 = 1,893 кН, то из уравнений находим
S9 = S4′ +S5′ cos300 = 6,01+1,893 0,866 = −4,371кН, S7 = F3 −S5′ sin300 = 3 −1,893 0,5 = 2,054кН.
Стержень 7 растянут, а стержень 9 сжат.
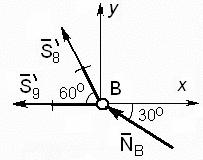
Вырежем узел H. Расчетная схема для него показана на рис.64. Неизвестным здесь является усилие в стержнях 8 – S8.
Узел H
Рис. 64
Уравнения равновесия для этого узла имеют вид
∑Fkx = −S6′ − F2 cos600 + S8 cos600 = 0,
∑Fky = −S7′ −S8 sin600 −F2 sin600 = 0.
Так как S’6 = S6 = -3,186 кН, то из первого уравнения находим
S | = F | + | S6′ | = 2 + −3,186 = −4,372кН. |
| ||||
8 | 2 | cos600 | 0,5 | |
|
|
| ||
Стержень 8 сжат. Второе уравнение используем для проверки уже найденного усилия S7
S7′ = −S8 sin600 − F2 sin600 = −(−4,372) 0,866 − 2 0,866 = = 2,054кН.
89
Усилия в стержне 7, найденные при вырезании узлов E и H, совпали.
Узел B можно использовать для проверки выполненного расчета. Вырежем узел B и рассмотрим его равновесие. Усилия в стержнях 8 и 9 будем считать неизвестными. Из уравнений равновесия для узла B определим эти усилия. Если они совпадут с соответствующими усилиями, найденными выше, то расчет верен, если нет – то следует искать ошибки в предыдущих вычислениях. Расчетная схема для узла B показана на рис. 65.
Узел B
Рис. 65
Уравнения равновесия для узла B имеют вид
∑Fkx = −S9′ −S8′ cos600 − NB cos300 = 0,
∑Fky =S8′ sin600 + NB sin300 = 0.
Решая эту систему уравнений, находим
sin300 |
| 0,5 |
|
S8′ = −NB sin600 | = −7,571 |
| = −4,371кН, |
0,866 | |||
S9′ = −S8′ cos600 | − NB cos300 = −(−4,371) 0,5 − 7,571 0,866 = | ||
= −4,371кН. |
|
|
|
Так как значения усилий в стержнях 8 и 9 совпали, то выполненные вычисления верны.
1 Связи и их реакции
Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными. Тела, ограничивающие свободу перемещения других тел, называются по отношению к ним связями.
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Шарнирно-неподвижная опора
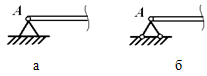
Шарнирно-подвижная опора Реакция направлена по нормали к опорной поверхности
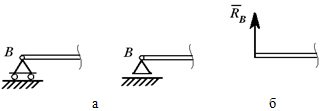 Соединение
стержня и втулки в плоскости–
скользящая заделка.
Соединение
стержня и втулки в плоскости–
скользящая заделка. 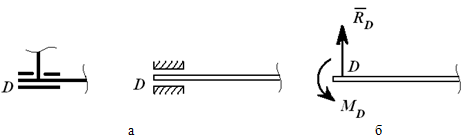 Бискользящая
заделка. В
плоскости данная опора допускает
поступательное перемещение стержня
как по горизонтали, так и по вертикали,
но препятствует повороту (в плоскости).
Реакцией такой опоры будет момент MC
Бискользящая
заделка. В
плоскости данная опора допускает
поступательное перемещение стержня
как по горизонтали, так и по вертикали,
но препятствует повороту (в плоскости).
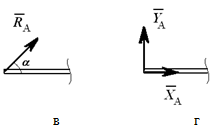
Реакцией такой опоры будет момент MC  Консоль (глухая или жесткая заделка) не допускает
никакого перемещения детали. Реакцией
такой опоры являются неизвестная по
величине и направлению сила RA с углом
α (или XA и YA ) и момент ΜA
Консоль (глухая или жесткая заделка) не допускает
никакого перемещения детали. Реакцией
такой опоры являются неизвестная по
величине и направлению сила RA с углом
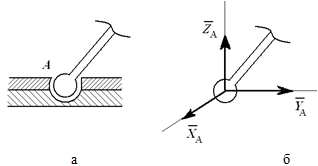
α (или XA и YA ) и момент ΜA 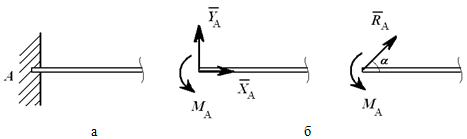 сферический
шарнир
сферический
шарнир
2Главный вектор и главный момент плоской системы сил
Рассмотрим плоскую систему сил (F1, F2, …, Fn),действующих на твердое тело в координатной плоскости Oxy.
Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:
R = F1 + F2 +
… + Fn = 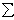 Fi.
Fi.
Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.
Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:
LO = MO(F1)
+ MO(F2)
+ … + MO(Fn)
= 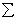 MO(Fi).
MO(Fi).
Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.
Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом LO плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментовэтих сил относительно центра О.
Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.
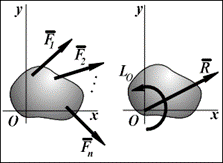
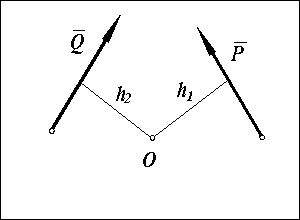
Правило знаков алгебраических моментов сил (в правой системе координат, принятой в механике): момент считается положительным, если сила стремится повернуть тело относительно точки О против хода часовой стрелки, и отрицательной — по ходу часовой стрелки.
Для сил P и Q, изображенных на рисунке, их алгебраические моменты относительно центра О равны: MО = P · h1; MO = -Q · h2.
3-4.Систем тел. Равновесие системы тел. Пример.
Статический расчет системы тел сводится к рассмотрению условий равновесия конструкций, состоящих из тел, соединенных какими-нибудь связями. Связи, соединяющие части конструкции называются внутренними, скрепляющие конструкцию с другими телами, в нее не входящими — внешними.
При решении задач статики реакции связей входят в число неизвестных, которые необходимо определить из уравнений равновесия. Система тел, для которых число неизвестныхреакций связей равно числу уравнений равновесия, называются статически определимыми. Система тел, для которых число неизвестных реакций связей больше числа уравненийравновесия, называются статически неопределимыми.
Если при отбрасывании внешних связей (опор) конструкция остается жесткой, то для нее задача о равновесии решается как для абсолютно твердого тела (при действии плоской системы сил число неизвестных реакций связей не должно быть больше трех).
Если после отбрасывания внешних связей конструкция не считается жесткой, то наиболее рациональным способом решения подобных задач является расчленение на отдельные тела и составление уравнений равновесия для каждого из тел в отдельности.
Для конструкции из n тел, на каждое из которых действует произвольная плоская система сил, получится таким путем 3n уравнений равновесия, позволяющих найти 3nнеизвестных.
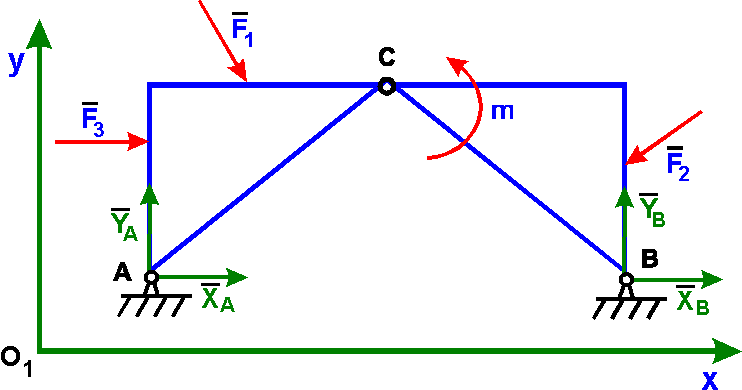 Например, если
отбросить опоры А и В трехшарнирной
арки, то она не будет жесткой: ее части
могут поворачиваться вокруг шарнира С.
Для определения реакций внешних
связей ХА, YА, ХВ, YВ
расчленим конструкцию по соединительному
шарниру С на
две части и рассмотрим равновесие
каждой из частей в отдельности.
Например, если
отбросить опоры А и В трехшарнирной
арки, то она не будет жесткой: ее части
могут поворачиваться вокруг шарнира С.
Для определения реакций внешних
связей ХА, YА, ХВ, YВ
расчленим конструкцию по соединительному
шарниру С на
две части и рассмотрим равновесие
каждой из частей в отдельности.
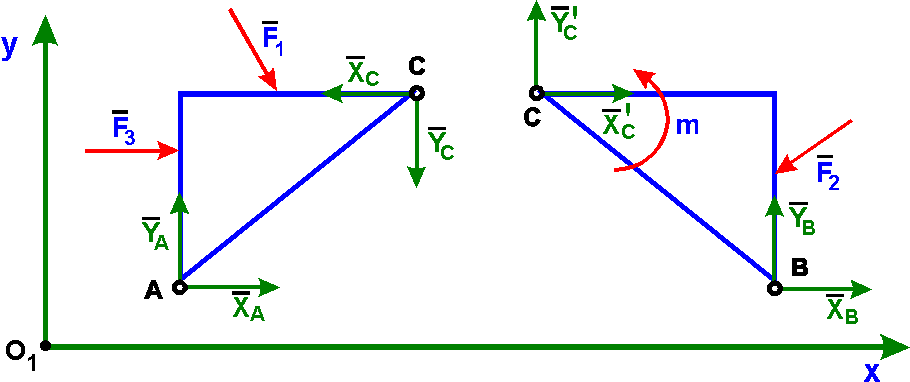
При действии на трехшарнирную арку произвольной плоской системы сил для каждой части можно записать три уравнений равновесия:
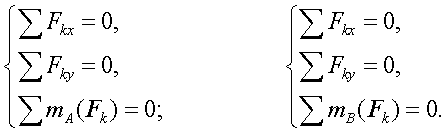 Присоединить к
этой системе шести уравнений на основании
закона о действии и противодействии
уравнения для узла С (ХС = ХСў, YС = YСў),
получим систему уравнений из которой
можно найти реакции внешних связей ХА,
YА, ХВ, YВ и реакции внутренних связей
ХС, YС.
Присоединить к
этой системе шести уравнений на основании
закона о действии и противодействии
уравнения для узла С (ХС = ХСў, YС = YСў),
получим систему уравнений из которой
можно найти реакции внешних связей ХА,
YА, ХВ, YВ и реакции внутренних связей
ХС, YС.
1.22. Определение реакций опор составных конструкций
Статически определимые задачи – задачи, в которых реакции внешних связей находятся из уравнений равновесия.
В
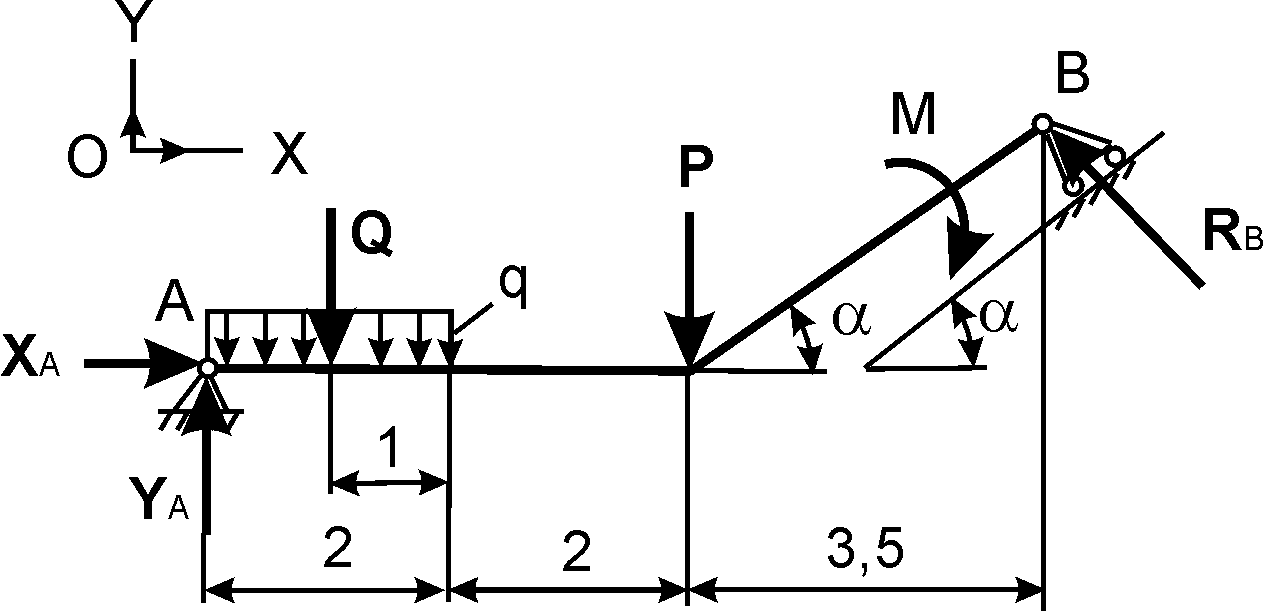
Рис. 1.60
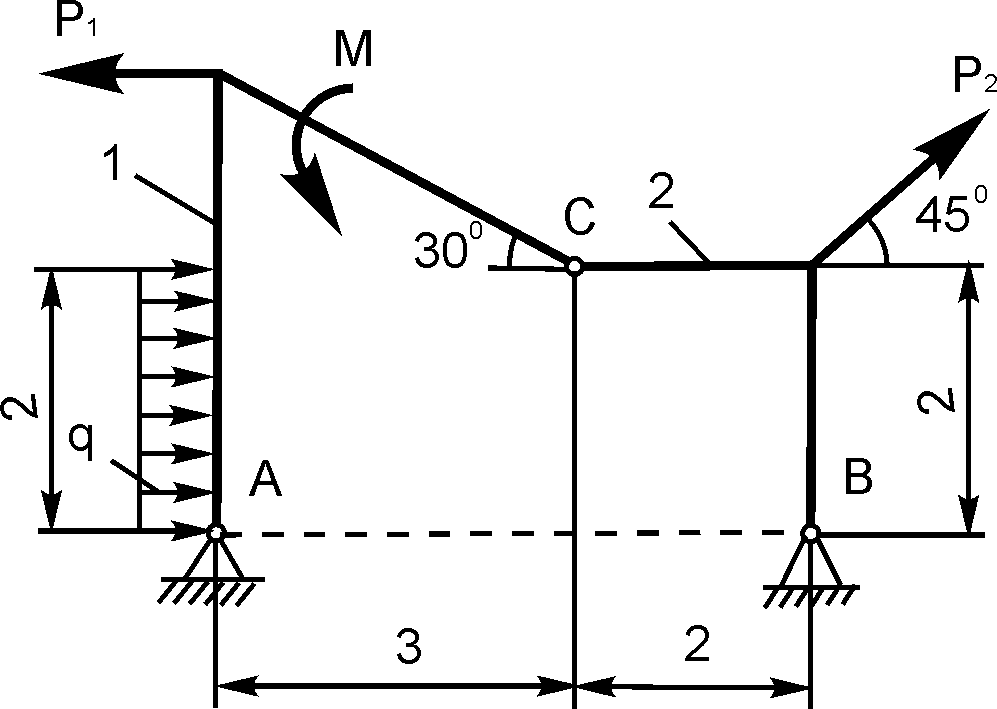
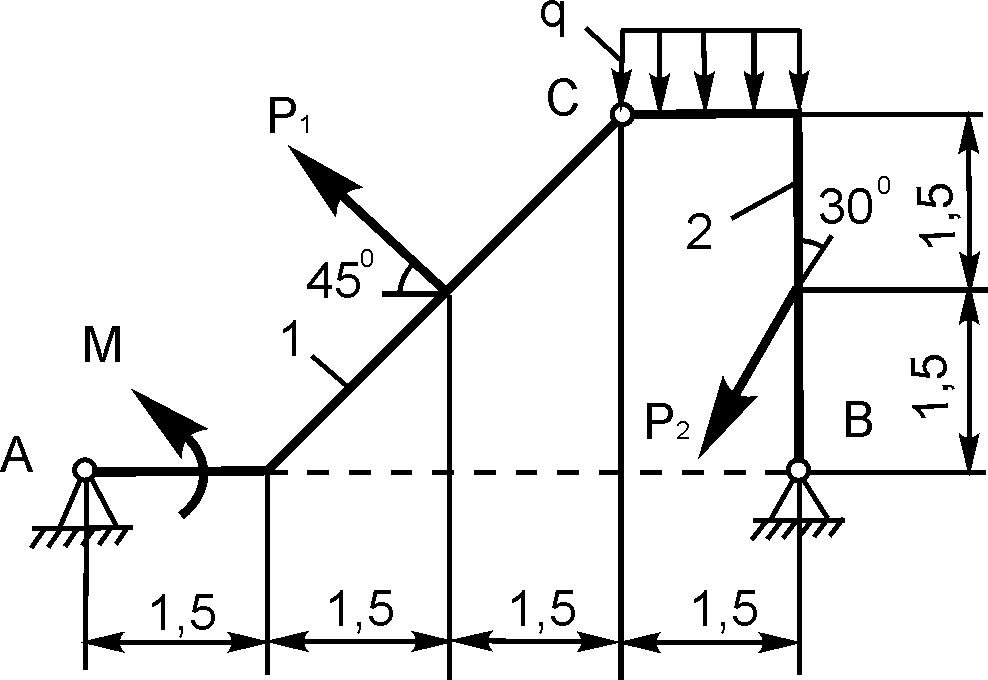
таких задачах число неизвестных реакций равно числу уравнений равновесия, которые могут быть составлены для механической системы (рис. 1.60).Дано: Р, М, q. Определить реакции внешних связей в точках А и В.
Порядок решения таких задач рассмотрен ранее, поэтому сразу же записывают уравнения равновесия для плоской произвольной системы сил:
∑ Fix = 0 = XА – RBsinα = 0; (1)
∑ FiY = 0 = YA – Q – P + RBcosα = 0; (2)
∑ MiA = 0 = – Q·1 – P·4 – M + RBsinα·3,5tgα + RBcosα·7,5 = 0. (3)
Очевидно, что из трех уравнений равновесия легко находятся реакции внешних связей XA, YA, RB.
Статически неопределимые задачи – задачи, в которых реакции внешних связей не могут быть найдены из уравнений статического равновесия, составленных для данной механической системы.
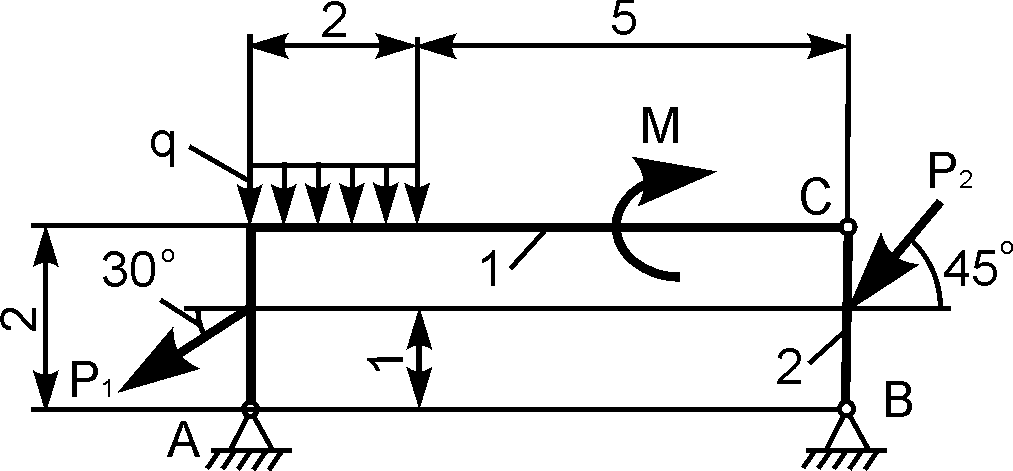
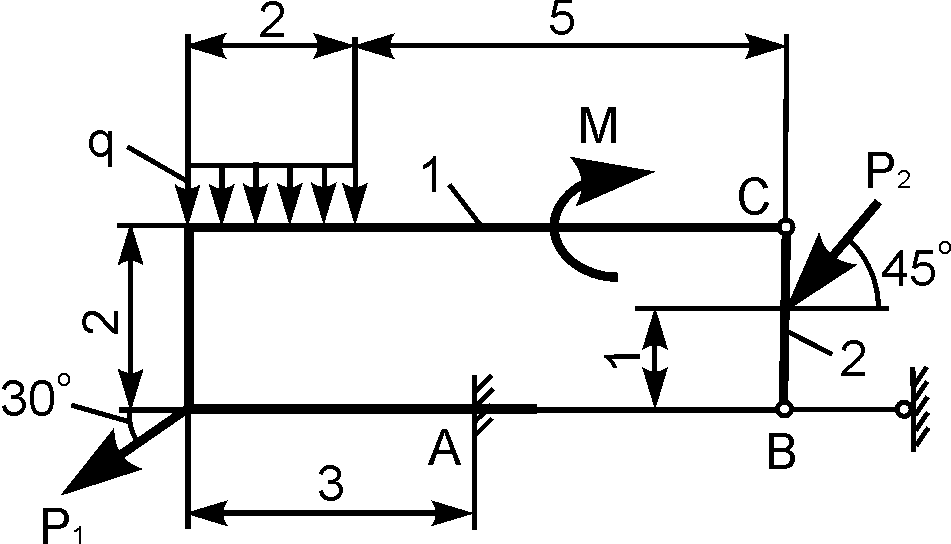
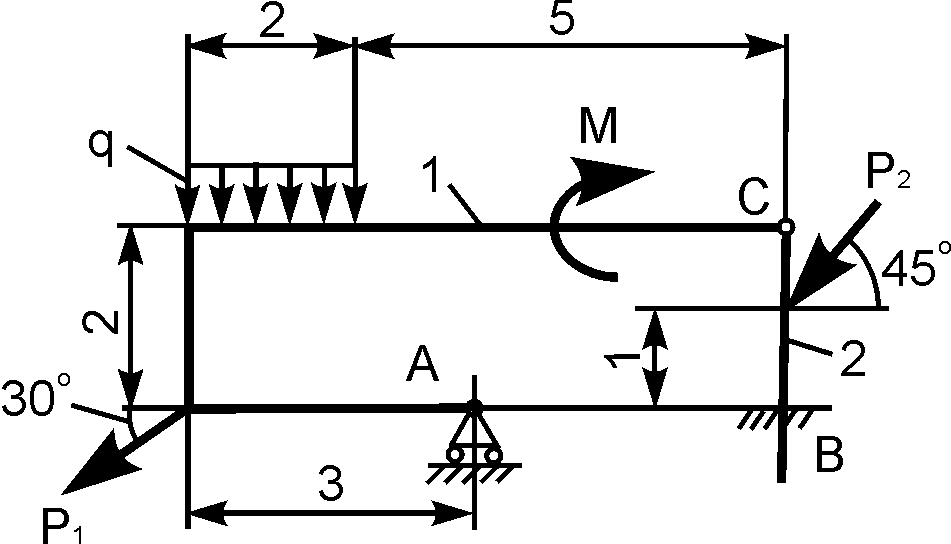
Для балки (рис. 1.61) можно составить только три уравнения равновесия, в которые входят четыре неизвестные реакции XA, YA, XB, YB.
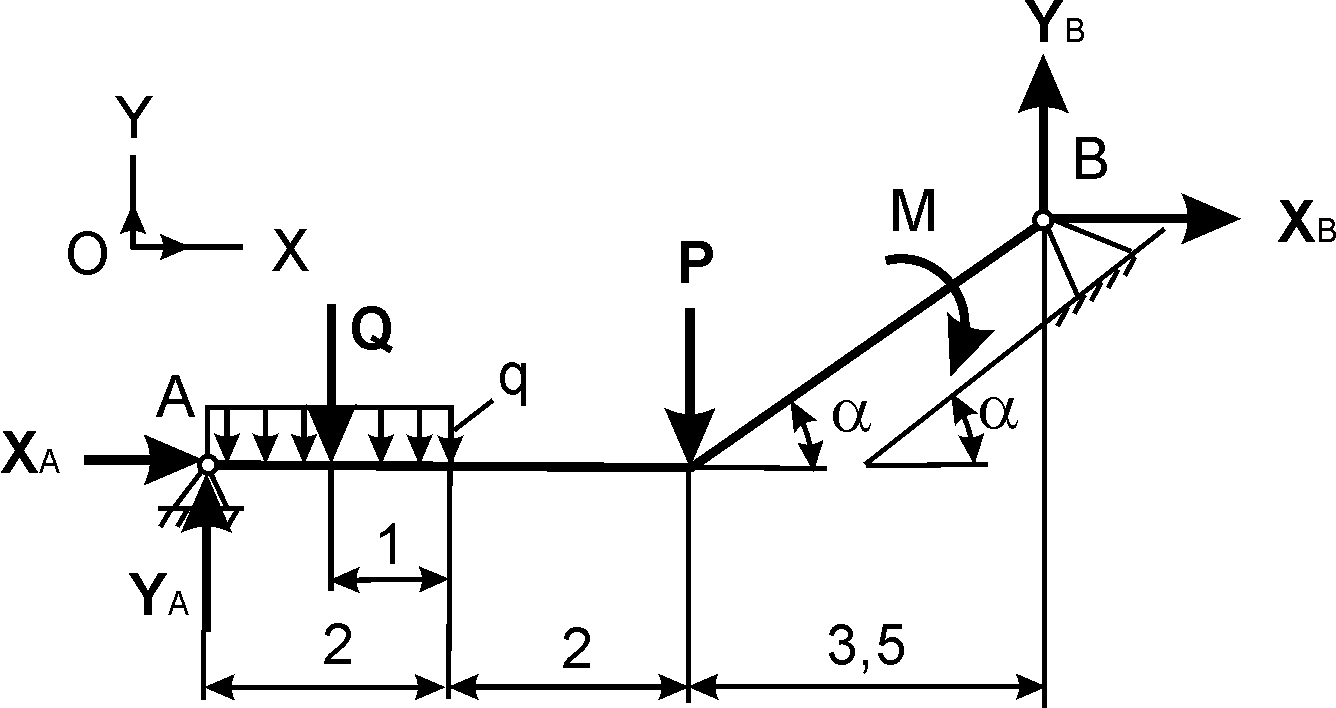
Рис. 1.61
Дано: Р, М, q. Определить реакции внешних связей в точках А и В.
Подробное решение такой задачи (статически неопределимой) рассматривается в курсе сопротивления материалов.
1.23. Алгоритм решения задач на определение реакций внешних связей для составных конструкций
Существует целый класс задач на равновесие составной конструкции, которые могут быть решены методами статики твердого тела. Решение таких задач проводится по следующему алгоритму.
Выбирается система отсчета.
Выделяется механическая система (составная конструкция), равновесие которой рассматривается.
К механической системе прикладываются активные нагрузки. Если задана распределенная нагрузка, то она приводится к сосредоточенной силе.
Согласно аксиоме связей внешние связи, наложенные на механическую систему, отбрасывают, и действие их заменяют соответствующими реакциями.
Записываются уравнения равновесия, соответствующие системе сил, действующей на составную конструкцию (система активных сил и реакций внешних связей).
Установив, что число неизвестных реакций внешних связей превышает число уравнений равновесия, составную конструкцию расчленяют по внутренним связям.
Рассматривают равновесие каждого из тел составной конструкции, которое находится в покое под действием активных сил, реакций внешних связей и реакций внутренних связей.
Для каждого из тел конструкции записывают соответствующие уравнения равновесия.
Полученную систему уравнений решают в наиболее удобной последовательности и находят неизвестные реакции внешних и внутренних связей.
Обычно при расчете используются не все уравнения равновесия, составленные для механической системы и для каждого из тел в отдельности. Поэтому оставшиеся уравнения используют для проверки полученных результатов.
1.24. Варианты курсового задания с 3 «Определение реакций опор составной конструкции (система двух тел)»
Методологию расчета реакций внешних связей, наложенных на составную конструкцию, рассмотрим на примере выполнения курсового задания С 3, которое входит в контрольную работу обучающегося.
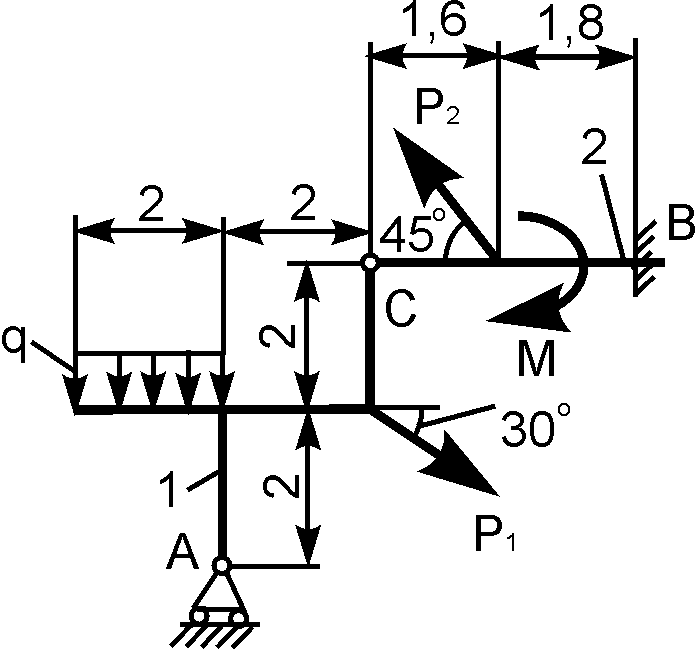
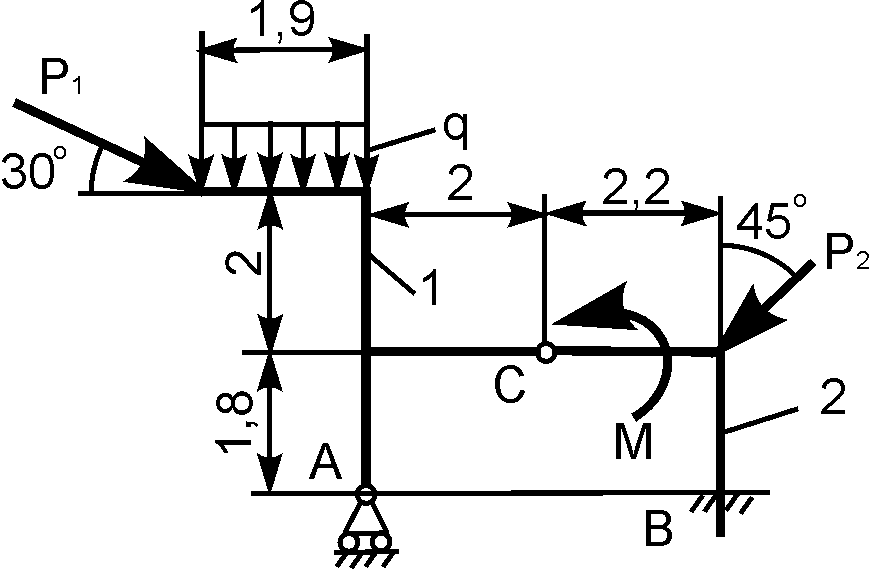
Конструкция состоит из двух тел. Определить реакции внешних связей, наложенных на составную конструкцию. Варианты расчетных схем конструкций и приложенные к ним нагрузки приведены в табл. 1.3.
Таблица 1.3
Номер варианта | Расчетная схема | Исходные данные | Определяемые величины |
1 | 2 | 3 | 4 |
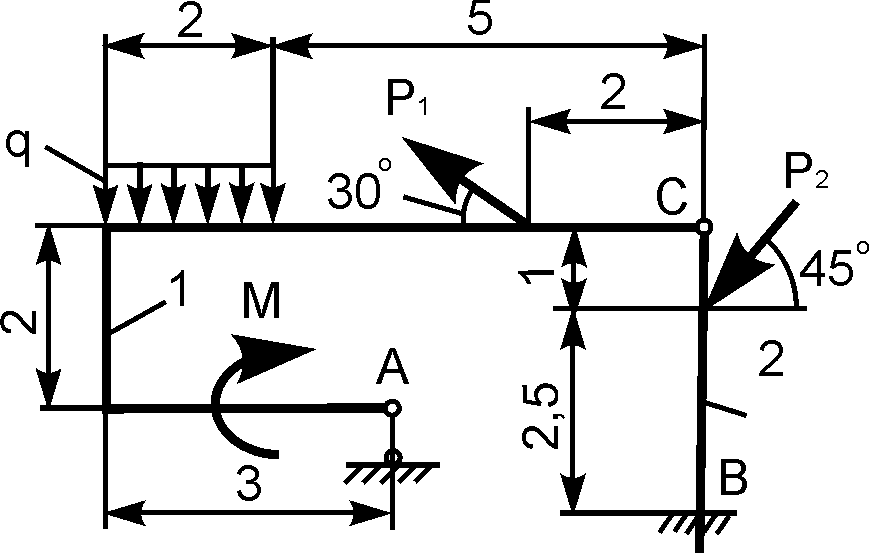
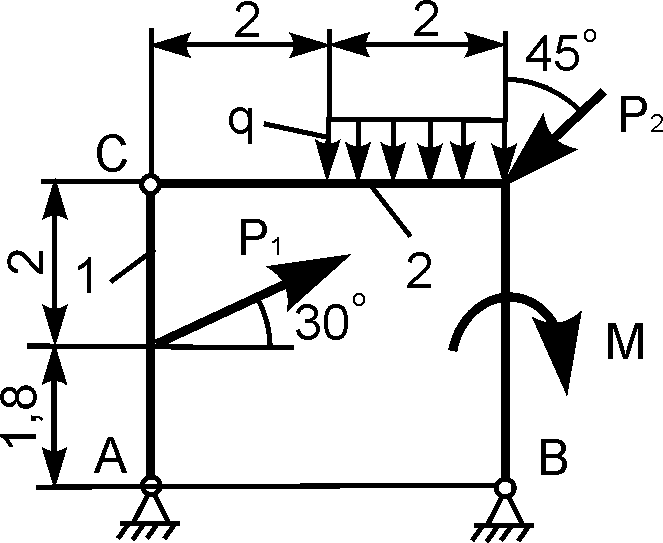
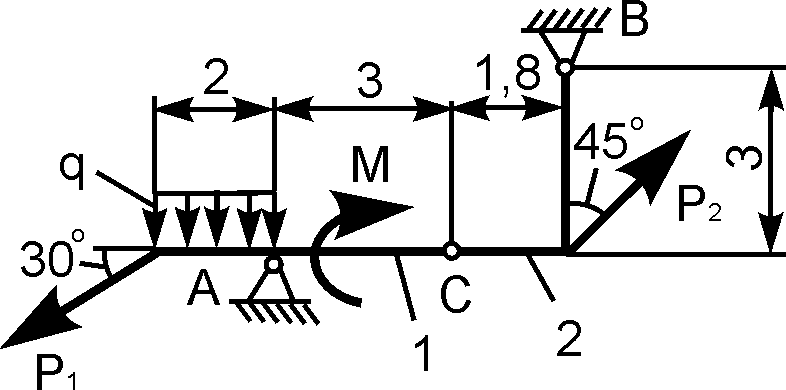
1 | | Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл
. 1.3
1 | 2 | 3 | 4 |
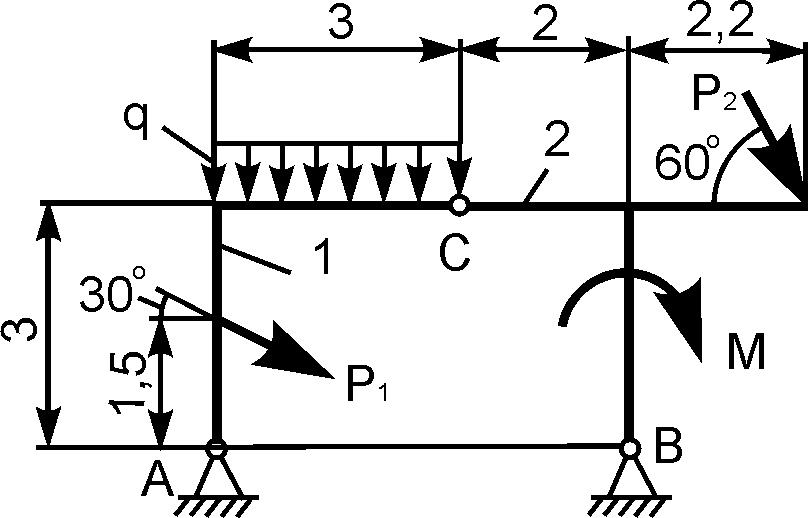
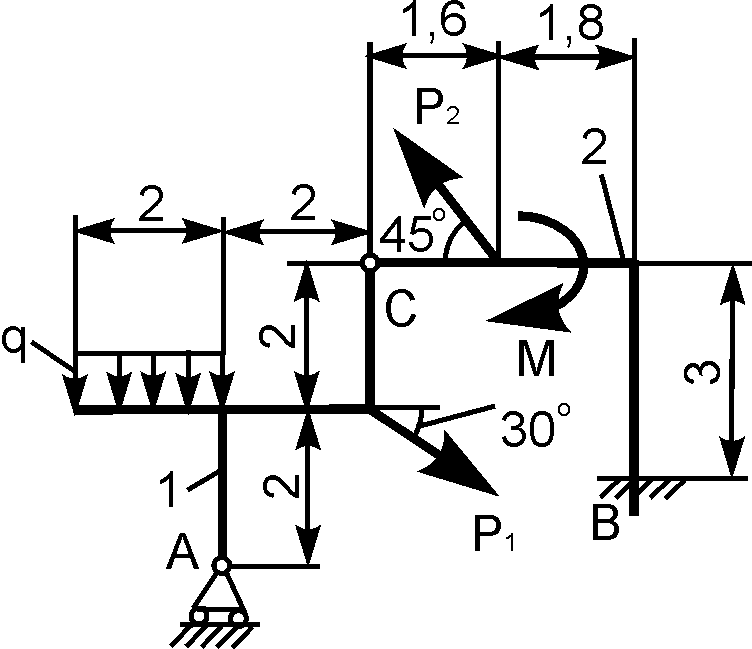
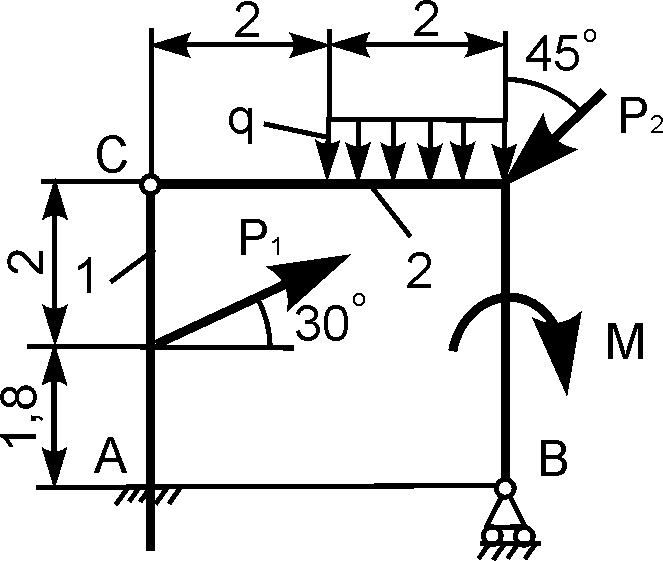
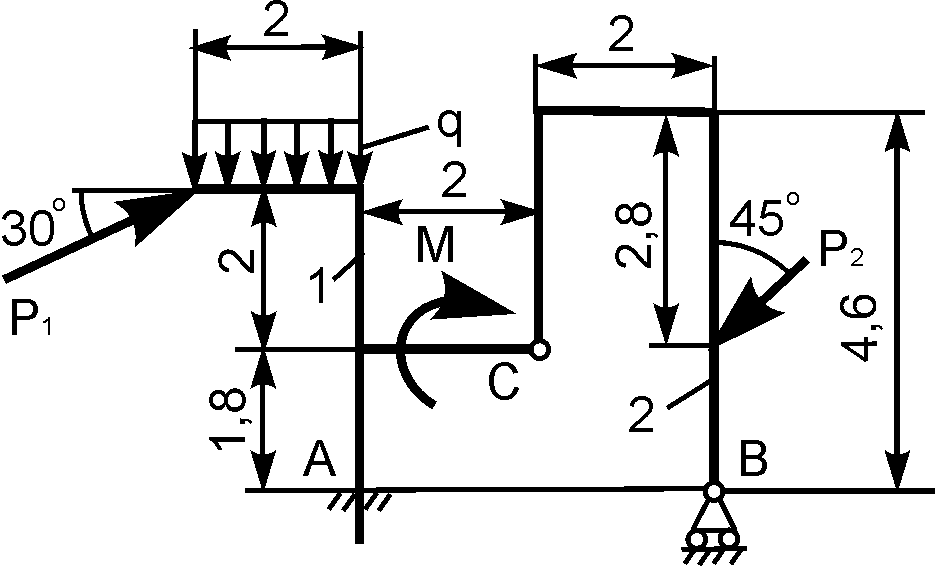
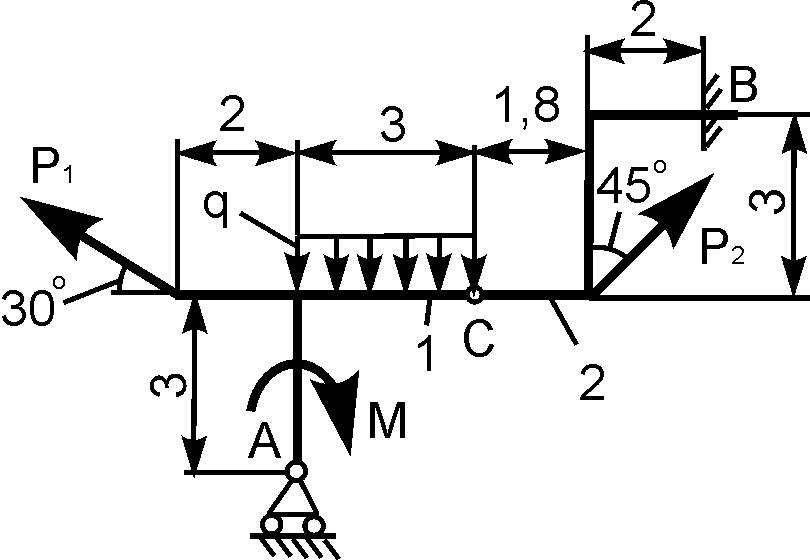
2 | | Р1 = 6 кН; Р2 = 10 кН; М = 12 кН·м; q = 1 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
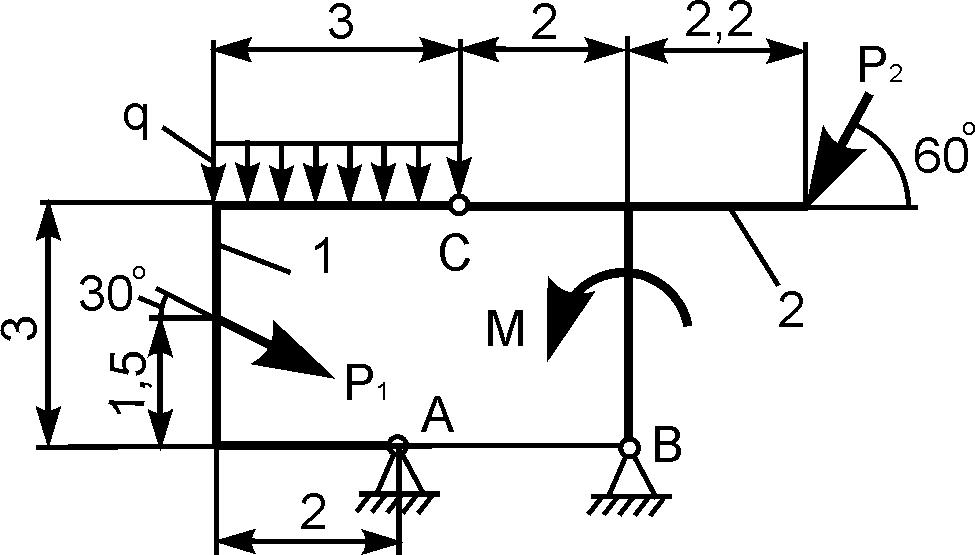
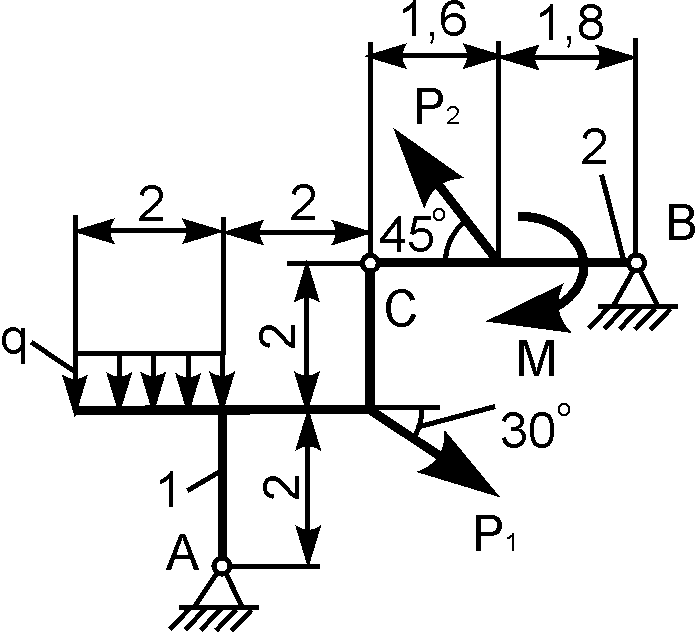
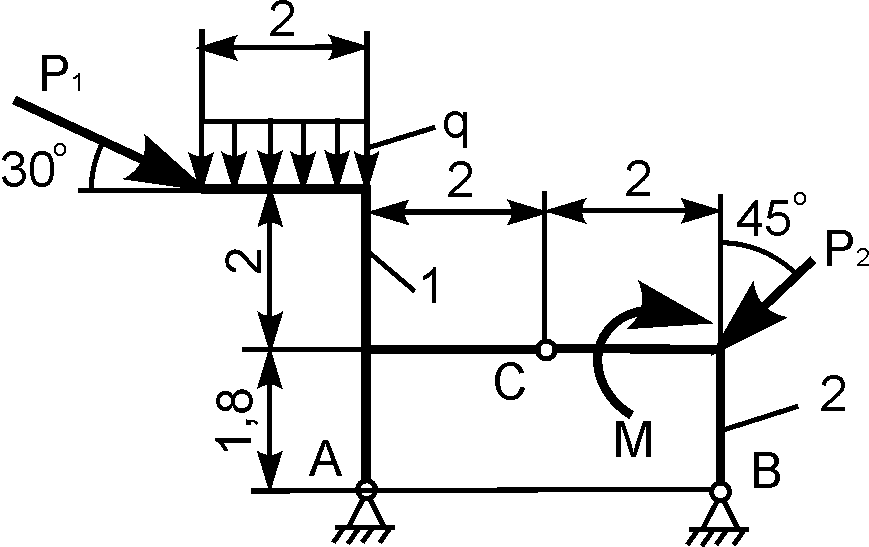
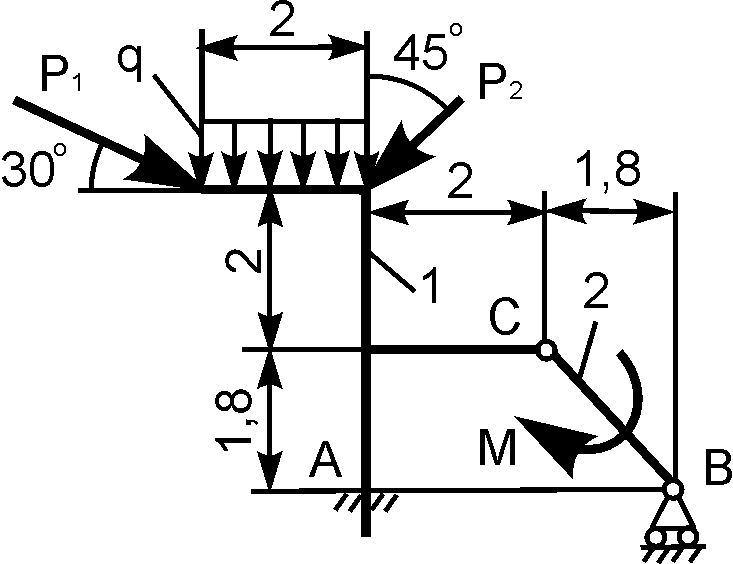
3 | | Р1 = 8 кН; Р2 = 10 кН; М = 3 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
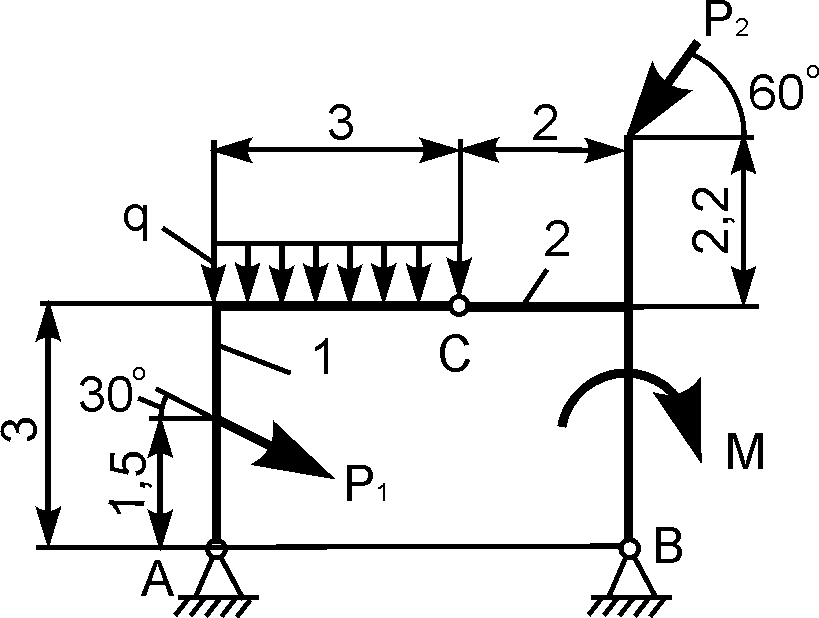
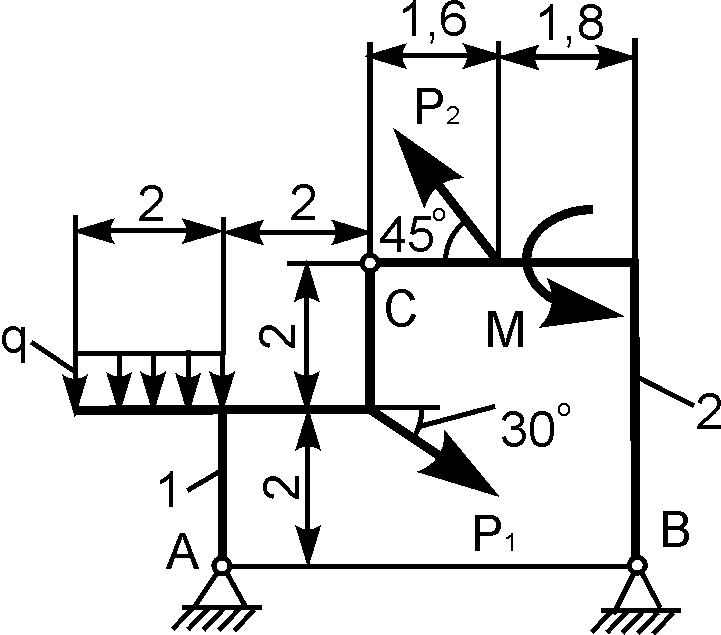
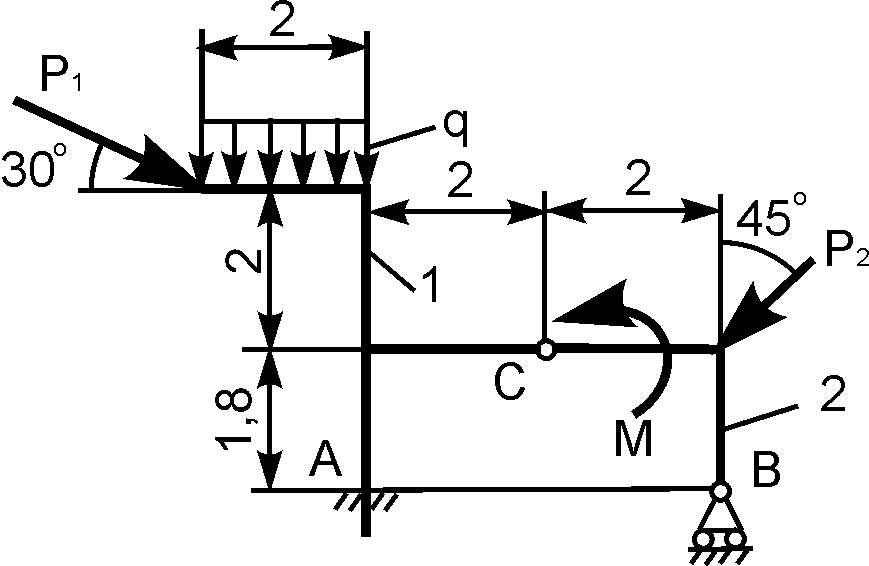
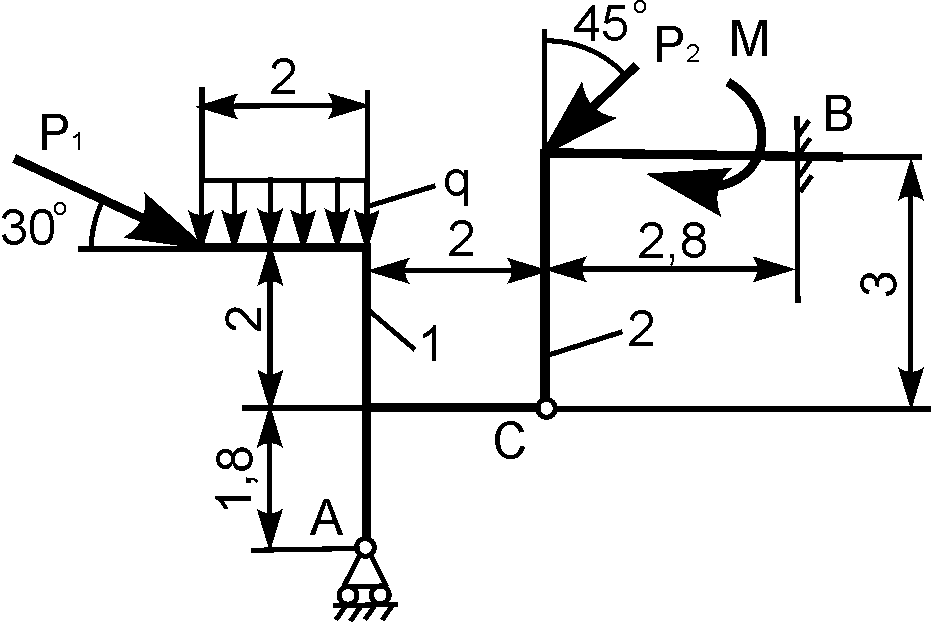
4 | | Р1 = 5 кН; Р2 = 12 кН; М = 4 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
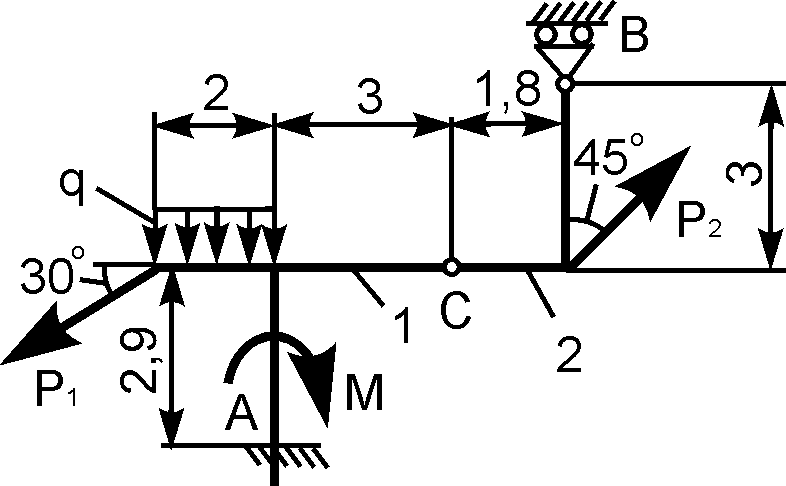
5 | | Р1 = 6 кН; Р2 = 8 кН; М = 3 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
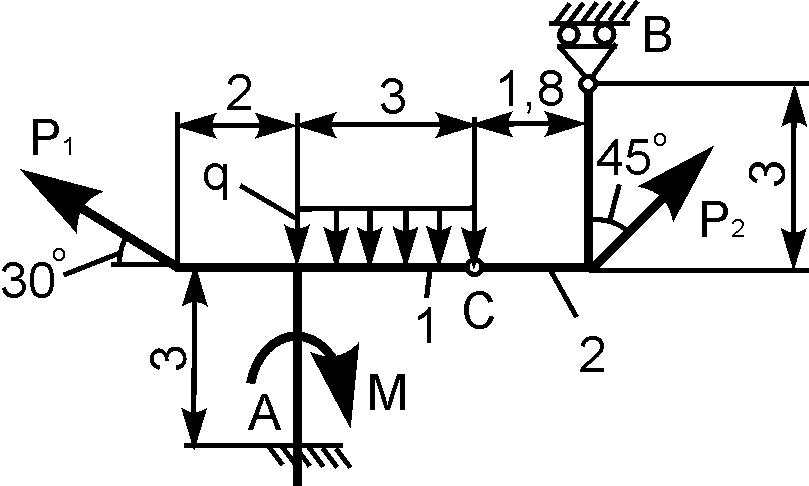
6 | | Р1 = 4 кН; Р2 = 6 кН; М = 10 кН·м; q = 2 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
7 | | Р1 = 7 кН; Р2 = 8 кН; М = 15 кН·м; q = 2 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
8 | | Р1 = 8 кН; Р2 = 8 кН; М = 16 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
9 | | Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
10 | | Р1 = 10 кН; Р2 = 3 кН; М = 9 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
11 | | Р1 = 12 кН; Р2 = 5 кН; М = 6 кН·м; q = 1 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
12 | | Р1 = 11 кН; Р2 = 3 кН; М = 8 кН·м; q = 4 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
13 | | Р1 = 10 кН; Р2 = 12 кН; М = 8 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
14 | | Р1 = 10 кН; Р2 = 2 кН; М = 12 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
15 | | Р1 = 15 кН; Р2 = 10 кН; М = 5 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
16 | | Р1 = 16 кН; Р2 = 10 кН; М = 4 кН·м; q = 1 кН/м | XA = ? YA = ? MA = ? RВ = ? |
17 | | Р1 = 17 кН; Р2 = 3 кН; М = 6 кН·м; q = 6 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
18 | | Р1 = 18 кН; Р2 = 9 кН; М = 4 кН·м; q = 8 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
19 | | Р1 = 19 кН; Р2 = 7 кН; М = 12 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
20 | | Р1 = 20 кН; Р2 = 12 кН; М = 8 кН·м; q = 4 кН/м | XA = ? YA = ? MA = ? RВ = ? |
21 | | Р1 = 21 кН; Р2 = 10 кН; М = 12 кН·м; q = 6 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
22 | | Р1 = 22 кН; Р2 = 12 кН; М = 10 кН·м; q = 5 кН/м | XA = ? YA = ? MA = ? RВ = ? |
23 | | Р1 = 23 кН; Р2 = 9 кН; М = 5 кН·м; q = 8 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
24 | | Р1 = 24 кН; Р2 = 10 кН; М = 12 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
25 | | Р1 = 25 кН; Р2 = 10 кН; М = 8 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
26 | | Р1 = 26 кН; Р2 = 16 кН; М = 6 кН·м; q = 6 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
27 | | Р1 = 27 кН; Р2 = 10 кН; М = 4 кН·м; q = 3 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
28 | | Р1 = 28 кН; Р2 = 18 кН; М = 8 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
29 | | Р1 = 28 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
Окончание табл. 1.3
1 | 2 | 3 | 4 |
30 | | Р1 = 30 кН; Р2 = 20 кН; М = 6 кН·м; q = 1 кН/м | RA = ? XB = ? YВ = ? MВ = ? |