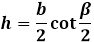Высота и длина – Высота равнобедренного треугольника | Формулы и расчеты онлайн

Все формулы для треугольника

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

 

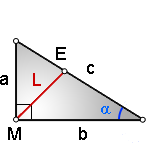
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)

a, b — катеты прямоугольного треугольника

с — гипотенуза

α — угол прилежащий к гипотенузе

 

Формула длины биссектрисы через катеты, ( L):

 

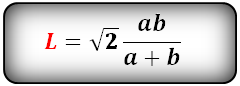
Формула длины биссектрисы через гипотенузу и угол, ( L):

 

 

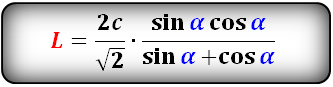
2. Найти по формулам длину биссектрисы из острого угла на катет:

 

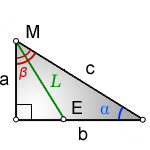
L — биссектриса, отрезок ME , исходящий из острого угла

a, b — катеты прямоугольного треугольника

с

— гипотенуза

α, β — углы прилежащие к гипотенузе

 

Формулы длины биссектрисы через катет и угол, (L):

 

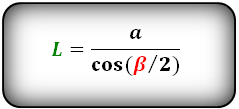
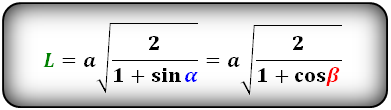
Формула длины биссектрисы через катет и гипотенузу, (L):

 

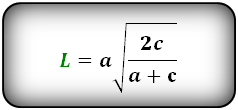
Длина — это… Что такое Длина?

Длина

Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине). В физике термин «длина» обычно используется как синоним «расстояния» и обозначается или .

Размерность длины — dim l = L. В ряду других пространственных величин длина — это величина единичной размерности, тогда как площадь — двухмерная, объём — трёхмерная. В большинстве систем измерений единица длины — одна из фундаментальных единиц измерения, на основе которых образуются другие единицы. В международной системе единиц (СИ) за единицу длины принят метр.

Единицы измерения длины

Относительные размеры
объектов, м.

-20 —

–

-18 —

–

-16 —

–

-14 —

–

-12 —

–

-10 —

–

-8 —

–

-6 —

–

-4 —

–

-2 —

–

0 —

–

2 —

–

4 —

–

6 —

–

8 —

–

10 —

–

12 —

–

14 —

–

16 —

–

18 —

–

20 —

–

22 —

–

24 —

–

26 —

–

28 —

–

30 —

Метрическая система

Метрическая система считается самой удобной из всех придуманных из-за своей простоты. В основе метрической системы лежит единица измерения метр. Все остальные единицы измерения являются кратными степеням десяти от метра (например, километр — это 10³ метров и т. п.), что позволяет облегчить подсчёты. До 1960 года у метра был специальный эталон, ныне хранящийся в Париже. Сегодня, по определению, метр равен расстоянию, которое проходит свет в вакууме за 1/299 792 458 долю секунды.

Британская/Американская система

Исходными английскими мерами длины были миля, ярд, фут и дюйм. Миля пришла в Англию из Древнего Рима, где она определялась как тысяча двойных шагов вооружённого римского воина.

Старорусская система

В Древней Руси мерой длины, веса и т. п. являлся человек. На это указывают названия мер длины: локоть (расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба), пядь (расстояние между вытянутым большим и указательным пальцами руки), сажень (расстояние от конца пальцев одной руки до конца пальцев другой) и другие

[1].

В частности, аршин был связан с длиной человеческого шага. Однако необходимость унификации систем измерений с британской в связи с развитием международной торговли потребовала введения во времена Петра I так называемого «казённого аршина». Это была мерная линейка с металлическими наконечниками с государственным клеймом. Казённый аршин равнялся 28 английским дюймам и делился на 16 вершков.^[2]

См. также

Древнегреческая система

Мусульманская система

• Ангушт или Асба (аналог дюйма)
• Пай (аналог фута)
• Ба или кама, равная приблизительно 2 м
• Касаба или наб
• Фарсах или парасанг, равный трём милям по 1000 Ба, или 6 км
• Барид, равный четырём фарсахам^[3]

Типографическая система

Морская система

Морская система измерения длины привязана к размеру планеты Земля. В качестве основной единицы измерения принята морская миля, равная длине одной минуты (1/60 градуса) дуги меридиана земного эллипсоида. Длина морской мили является величиной переменной, зависящей от широты. Ее численное значение составляет от 1843 метров на экваторе до 1861,6 метров на полюсах.

Международная морская миля составляет 1852 м, в отличие от морской мили Британской системы (1853,184 м). Для измерения меньших размеров применяют кабельтов — 1/10 морской мили, или 185,2 м (округлённо — 185 м).^[4]

Единицы, применяемые в астрономии

Измерительные инструменты и меры

Измерительные приборы

Другие средства

• Большие расстояния в навигации определяются при помощи средств радионавигационных систем или спутниковых систем
• Очень маленькие расстояния измеряются с помощью измерительных микроскопов

См. также

Примечания

Категории:

• Физические величины по алфавиту
• Метрология

Wikimedia Foundation. 2010.

Размер шрифта, высота и длина строки по Золотому Сечению

В течение нескольких последних дней я прокручивал в своей голове вопрос “какова же идеальная высота строки для размера шрифта в 14px на моем экране?”

Я просмотрел множество сайтов, чтобы определить, как же люди её вычисляют, и обнаружил несколько интересных цифр:

Высота строки

Фреймворк Twitter Bootstrap использует цифру (1.42857) как отношение между размером шрифта и высотой строки (line-height = font-size * 1.42857).

HTML5 boilerplate используе почти ту же цифру:

(1.4).

Medium и zurb foundation фреймворк используют одно и то же значение для высоты строки, которое равно (1.5).

Возможно вам также будет интересно, что adobe topcoat остановился на цифре (1.313), а yahoo purecss использует (1.58). Так какое же отношение выбрать?

Помните, что отношение 1.5 – это то значение, которое является рекомендованным в классических типографических книгах.

Основы типографики для начинающих дизайнеров

Лично я не знаю, какое отношение использовать, и откуда взялись те цифры, которые используют в примерах выше. Могу ли я использовать своё собственное число?

Природа дала нам невероятную пропорцию, которая окружает нас повсюду, под названием золотое сечение (1.618), так что я планирую использовать его для определения высоты строки (14px * 1.618). Таким образом, я нашел ответ на свой первоначальный вопрос, но тут сразу же возник следующий:

“Какова же лучшая ширина строки для размера шрифта в 14px и высоты строки в 23px?”

Ширина строки

Так как же определить взаимосвязь размера шрифта и ширины строки? Всё что я знаю – это то, что ширина строки значительно больше высоты. Для начала неплохо!

Прочитав несколько исследований о лучшем количестве символов в строке (СВС), я обнаружил, что более 60% всех людей читают быстрее с 70 СВС. Вот краткий вывод:

Текст с длиной строки в 55 СВС лучше и быстрее читается, а информация усваивается лучше, чем при длине строки в 25 или 100 символов.

Оптимальная ширина строки в одной колонке варируется от 45 до 75 СВС. Для нескольких колонок длина строки должна быть от 30 до 50 СВС.

Ширина строки должна быть примерно в 30 раз (от 20 до 40) больше размера шрифта.

Люди предпочитают короткие строки в 8-10 слов или от 45 до 60 символов.

Никакого фиксированного значения для ширины строки не существует, но идеальное значение находится где-то между (30-90 СВС) или (8-12 словами).

Давайте рассчитаем ширину строки:

ширина строки = средняя ширина символа * СВС

Средняя ширина символа = размер шрифта / константа (1.618)

В итоге имеем:

Размер шрифта = 14px

Высота строки = (14 * 1.618) = 23px

Ширина строки на 50 СВС = 50 * (14 / 1.618) = 433px

Ускорить процесс вычисления оптимальной высоты и ширины строки в вашем следующем проекте можно с помощью SASS операторов и переменных.

Демо

В этой демо вы можете испытать разные комбинации высоты и ширины строки.

---

Перевод статьи: Font size, line height and line width the golden ratio way

Чем отличается длинна от высоты?

Разные измерения — еще ширина есть

длинна это когда лежит, а высота это когда стоит!!!

длина это——— высота это! ! !

Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера)… Высота́ — измерение объекта или его местоположения, отмеряемое в вертикальном направлении. В толковом словаре Ушакова определена как «протяжение снизу вверх, вышина»

Как посчитать высоту равнобедренного треугольника

Чтобы посчитать чему равна высота равнобедренного треугольника просто воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

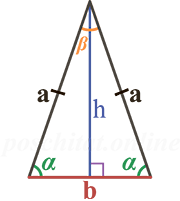
Чтобы вычислить высоту равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):

• длину двух равных сторон (a) и длину основания (b)
• длину двух равных сторон (a) и угол α
• длину двух равных сторон (a) и угол β
• длину основания (b) и угол α
• длину основания (b) и угол β

Введите их в соответствующие поля и получите результат.

Если известны длина стороны а и основания b

Чему равна высота h у равнобедренного треугольника если известны длина стороны a и длина основания b?

Формула

h = √a² — (^b/₂)²

Пример

Если сторона a = 10 см, а сторона b = 5 см, то:

h = √10² — (⁵/₂)² = √100 — 6.25 ≈ 9.68 см

Если известны длина стороны а и угол α

Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол α?

Формула

h = a⋅sin α

Пример

Если сторона a = 5 см, а ∠α = 45°, то:

h = 5⋅sin 45 ≈ 3,53 см

Если известны длина стороны а и угол β

Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол β?

Формула

h = a⋅cos ^β/₂

Пример

Если сторона a = 5 см, а ∠β = 30°, то:

h = 5⋅cos ³⁰/₂ ≈ 4.83 см

Если известны длина стороны b и угол α

Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол α?

Формула

h = ^b/₂⋅tg α

Пример

Если сторона b = 20 см, а ∠α = 35°, то:

h = ²⁰/₂⋅tg 35 = 10⋅0.7 = 7 см

Если известны длина стороны b и угол β

Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол β?

Формула

h = ^b/₂⋅ctg ^β/₂

Пример

Если сторона b = 15 см, а ∠β = 40°, то:

h = ¹⁵/₂⋅ctg ⁴⁰/₂ = 7.5⋅2.7474 ≈ 20.6 см

См. также

Все формулы высоты прямого угла в прямоугольном треугольнике

---

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.

 

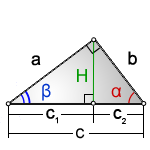H — высота из прямого угла

a, b — катеты

с — гипотенуза

c₁ , c₂ — отрезки полученные от деления гипотенузы, высотой

α, β — углы при гипотенузе

 

Формула длины высоты через стороны, (H):

 

 

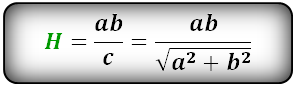
Формула длины высоты через гипотенузу и острые углы, (H):

 

Формула длины высоты через катет и угол, (H):

 

Формула длины высоты через составные отрезки гипотенузы , (H):

---

---

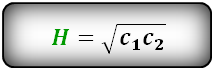
Подробности

Автор: Administrator

Опубликовано: 09 октября 2011

Обновлено: 16 мая 2017

Высота равнобедренного треугольника | Онлайн калькулятор

Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.

Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам — это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника решаются через прямоугольные треугольники, которые она образует.

Рассмотрим каждый случай по отдельности.

Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.

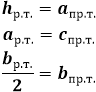
Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:

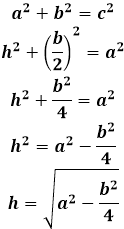
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.

Площадь любого треугольника можно найти несколькими способами — например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.

Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:

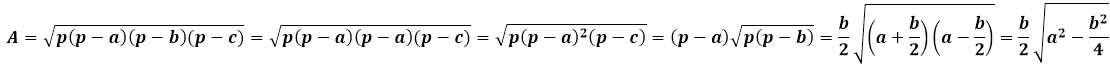
Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне

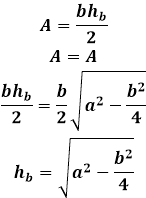
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.

Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sin⁡α

Формула через боковую сторону и угол напротив основания β:

Формула через основание и угол при нем α:

через основание и угол противолежащий ему β: