Расчет статически определимой фермы | ПроСопромат.ру
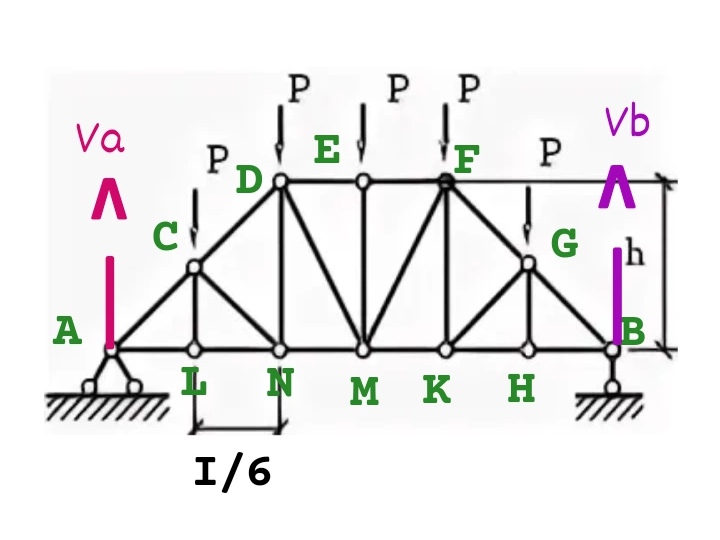
Статически определимая ферма. Задача. Определить усилия в стержнях фермы второй панели слева и стойки справа от панели, а также срединной стойки аналитическими методами. Дано: d=2м; h=3м; ℓ=16м; F=5кН.
Рассмотрим ферму с симметричным загружением.
Сначала обозначим опоры буквами А и В, нанесем опорные реакции RА и RВ.
Определим реакции из уравнений статики. Поскольку загрузка фермы симметрична, реакции будут равны между собой:
Если загрузка фермы несимметричная, то реакции определяются как для балки с составлением уравнений равновесия ∑МА=0 (находим 
Теперь обозначим элементы фермы:
«О» — стержни верхнего пояса (ВП),
«U» — стержни нижнего пояса (НП),
«V» — стойки,
«D» — раскосы.
С помощью этих обозначений удобно называть усилия в стержнях, н.р., О4 — усилие в стержне верхнего пояса; D2
Затем обозначим цифрами узлы фермы. Узлы А и В уже обозначены, на остальных расставим цифры слева направо с 1 по 14.
Согласно заданию, нам предстоит определить усилия в стержнях О2, D1, U2 (стержни второй панели), усилие в стойке V2, а также усилие в срединной стойке V4 .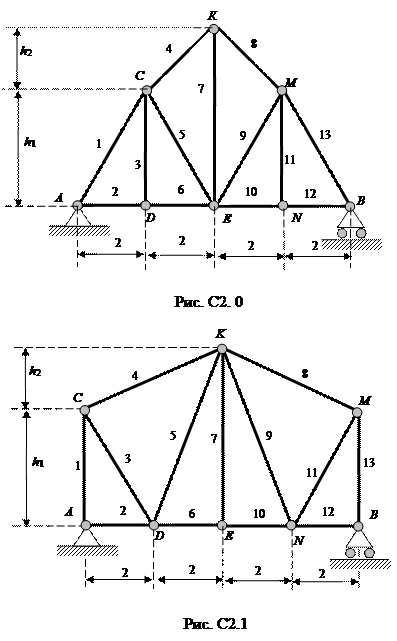 Существуют три аналитических метода определения усилий в стержнях.
Существуют три аналитических метода определения усилий в стержнях.
- Метод моментной точки (метод Риттера),
- Метод проекций,
- Метод вырезания узлов.
Первые два метода применяется только тогда, когда ферму можно рассечь на две части сечением, проходящим через 3 (три) стержня. Проведем сечение 1-1 во второй панели слева.
Сеч. 1-1 рассекает ферму на две части и проходит по трем стержням — О2, D1, U2. Рассматривать можно любую часть – правую или левую, неизвестные усилия в стержнях направляем всегда
Рассмотрим левую часть фермы, покажем ее отдельно. Направляем усилия, показываем все нагрузки.
Сечение проходит по трем стержням, значит можно применить метод моментной точки. Моментной точкой для стержня называется точка пересечения двух других стержней, попадающих в сечение.
Моментной точкой для стержня называется точка пересечения двух других стержней, попадающих в сечение.
Определим усилие в стержне О2.
Моментной точкой для О2будет т.14
Составим уравнение моментов относительно т. 14 (рассматриваем левую часть).
О2мы направили от узла, полагая растяжение, а при вычислении получили знак «-», значит, стержень О2 – сжат.
Далее в скобках будет указывать деформацию стержня – сжат или растянут.
Определяем усилия в стержне U2. Для U2 моментной точкой будет  2, т.к. в ней пересекаются два других стержня — О2 и D1.
2, т.к. в ней пересекаются два других стержня — О2 и D1.
Теперь определяем моментную точку для D1. Как видно из схемы, такой точки не существует, поскольку усилия О2 и U2 не могут пересекаться, т.к. параллельны. Значит, метод моментной точки неприменим.
Воспользуемся методом проекций. Для этого спроецируем все силы на вертикальную ось У
Определим усилие в правой стойке V2. Через эту стойку можно провести сечение, которое проходило бы по трем стержням. Покажем сечение 2-2, оно проходит через стержни О3, V2, U2. Рассмотрим левую часть.
Рассмотрим левую часть.
Как видно из схемы, метод моментной точки в данном случае неприменим, применим метод проекций
Теперь определим усилие в срединной стойке V4. Через эту стойку нельзя провести сечение, чтобы оно делило ферму на две части и проходило бы через три стержня, значит, методы моментной точки и проекций здесь не подходят. Применим метод вырезания узлов. Стойка V4 примыкает к двум узлам – узлу 4 (вверху) и к узлу 11 (внизу). Выбираем узел, в котором наименьшее количество стержней, т.е. узел 11. Вырезаем его и помещаем в координатные оси таким образом, чтобы одно из неизвестных усилий проходило бы по одной из осей
 Усилия, как и прежде, направляем от узла, предполагая растяжение.
Усилия, как и прежде, направляем от узла, предполагая растяжение.Узел 11.
Проецируем усилия на координатные оси
∑х=0, —U4+ U5=0, U4= U5
∑у=0, V4=0.
Таким образом, стержень
Нулевым стержнем называется стержень фермы, в которой усилие равно 0.
Правила определения нулевых стержней — смотреть здесь.
Если в симметричной ферме при симметричном загружении требуется определить усилия во всех стержнях, то следует определить усилия любыми методами в одной части фермы, во второй части в симметричных стержнях усилия будут идентичны.
Все усилия в стержнях удобно свести в таблицу (на примере рассматриваемой фермы).
Расчёт плоских статически определимых ферм основными методами ручного счёта; расчёт на ЭВМ
Фермами называют плоские и пространственные стержневые конструкции с шарнирными соединениями элементов, загружаемые исключительно в узлах. Шарнир допускает вращение, поэтому считается, что стержни под нагрузкой работают только на центральное растяжение-сжатие. Фермы позволяют значительно сэкономить материал при перекрытии больших пролётов.
- Способ проекций
- Метод вырезания узла
- Метод сечений
- Способ моментной точки
- Признаки нулевого стержня
- Расчёт ферм на персональном компьютере
- Порядок работы в программе Полюс
Рисунок 1
- по очертанию внешнего контура;
- по виду решётки;
- по способу опирания;
- по назначению;
- по уровню проезда транспорта.

Также выделяют простейшие и сложные фермы. Простейшими называют фермы, образованные последовательным присоединением шарнирного треугольника. Такие конструкции отличаются геометрической неизменяемостью, статической определимостью. Фермы со сложной структурой, как правило, статически неопределимы.
Для успешного расчёта необходимо знать виды связей и уметь определять реакции опор. Эти задачи подробно рассматриваются в курсе теоретической механики. Разницу между нагрузкой и внутренним усилием, а также первичные навыки определения последних дают в курсе сопротивления материалов.
Рассмотрим основные методы расчёта статически определимых плоских ферм.
Способ проекций
На рис. 2 симметричная шарнирно-опёртая раскосная ферма пролётом L = 30 м, состоящая из шести панелей 5 на 5 метров. К верхнему поясу приложены единичные нагрузки P = 10 кН. Определим продольные усилия в стержнях фермы. Собственным весом элементов пренебрегаем.
Собственным весом элементов пренебрегаем.
Рисунок 2
Опорные реакции определяются путём приведения фермы к балке на двух шарнирных опорах. Величина реакций составит R (A) = R (B) = ∑P/2 = 25 кН. Строим балочную эпюру моментов, а на её основе — балочную эпюру поперечных усилий (она понадобится для проверки). За положительное направление принимаем то, что будет закручивать среднюю линию балки по часовой стрелке.
Рисунок 3
Метод вырезания узла
Метод вырезания узла заключается в отсечении отдельно взятого узла конструкции с обязательной заменой разрезаемых стержней внутренними усилиями с последующим составлением уравнений равновесия. Суммы проекций сил на оси координат должны равняться нулю. Прикладываемые усилия изначально предполагаются растягивающими, то есть направленными от узла. Истинное направление внутренних усилий определится в ходе расчёта и обозначится его знаком.
youtube.com/embed/DWsFr61blCY»>Рационально начинать с узла, в котором сходится не более двух стержней. Составим уравнения равновесия для опоры, А (рис. 4).
∑ F (y) = 0: R (A) + N (A-1) = 0
∑ F (x) = 0: N (A-8) = 0
Очевидно, что N (A-1) = -25кН. Знак «минус» означает сжатие, усилие направлено в узел (мы отразим это на финальной эпюре).
Условие равновесия для узла 1:
∑ F (y) = 0: -N (A-1) — N (1−8)∙cos45° = 0
∑ F (x) = 0: N (1−2) + N (1−8)∙sin45° = 0
Из первого выражения получаем N (1−8) = —N (A-1)/cos45° = 25кН/0,707 = 35,4 кН. Значение положительное, раскос испытывает растяжение. N (1−2) = -25 кН, верхний пояс сжимается. По этому принципу можно рассчитать всю конструкцию (рис. 4).
Рисунок 4
Метод сечений
Ферму мысленно разделяют сечением, проходящим как минимум по трём стержням, два из которых параллельны друг другу. Затем рассматривают равновесие одной из частей конструкции. Сечение подбирают таким образом, чтобы сумма проекций сил содержала одну неизвестную величину.
Затем рассматривают равновесие одной из частей конструкции. Сечение подбирают таким образом, чтобы сумма проекций сил содержала одну неизвестную величину.
Проведём сечение I-I (рис. 5) и отбросим правую часть. Заменим стержни растягивающими усилиями. Просуммируем силы по осям:
∑ F(y) = 0: R(A) — P + N(9−3)
N(9−3) = P — R(A) = 10 кН — 25 кН = -15 кН
Стойка 9−3 сжимается.
Рисунок 5
Способ проекций удобно применять в расчётах ферм с параллельными поясами, загруженными вертикальной нагрузкой. В этом случае не придётся вычислять углы наклона усилий к ортогональным осям координат. Последовательно вырезая узлы и проводя сечения, мы получим значения усилий во всех частях конструкции. Недостатком способа проекций является то, что ошибочный результат на ранних этапах расчёта повлечёт за собой ошибки во всех дальнейших вычислениях.
Способ моментной точки
Способ моментной точки требует составлять уравнение моментов относительно точки пересечения двух неизвестных сил. Как и в методе сечений, три стержня (один из которых не пересекается с остальными) разрезаются и заменяются растягивающими усилиями.
Как и в методе сечений, три стержня (один из которых не пересекается с остальными) разрезаются и заменяются растягивающими усилиями.
Рассмотрим сечение II-II (рис. 5). Стержни 3−4 и 3−10 пересекаются в узле 3, стержни 3−10 и 9−10 пересекаются в узле 10 (точка K). Составим уравнения моментов. Суммы моментов относительно точек пересечения будут равняться нулю. Положительным принимаем момент, вращающий конструкцию по часовой стрелке.
∑ m(3) = 0: 2d∙R(A) — d∙P — h∙N(9−10) = 0
∑ m(K) = 0: 3d∙R(A) — 2d∙P — d∙P + h∙N(3−4) = 0
Из уравнений выражаем неизвестные:
N(9−10) = (2d∙R(A) — d∙P)/h = (2∙5м∙25кН — 5м∙10кН)/5м = 40 кН (растяжение)
N(3−4) = (-3d∙R(A) + 2d∙P + d∙P)/h = (-3∙5м∙25кН + 2∙5м∙10кН + 5м∙10кН)/5м = -45 кН (сжатие)
Способ моментной точки позволяет определить внутренние усилия независимо друг от друга, поэтому влияние одного ошибочного результата на качество последующих вычислений исключено. Данным способом можно воспользоваться в расчёте некоторых сложных статически определимых ферм (рис. 6).
Данным способом можно воспользоваться в расчёте некоторых сложных статически определимых ферм (рис. 6).
Рисунок 6
Требуется определить усилие в верхнем поясе 7−9. Известны размеры d и h, нагрузка P. Реакции опор R(A) = R(B) = 4,5P. Проведём сечение I-I и просуммируем моменты относительно точки 10. Усилия от раскосов и нижнего пояса не попадут в уравнение равновесия, так как сходятся в точке 10. Так мы избавляемся от пяти из шести неизвестных:
∑ m(10) = 0: 4d∙R(A) — d∙P∙(4+3+2+1) + h∙O(7−9) = 0
O(7−9) = -8d∙P/h
Аналогично можно рассчитать остальные стержни верхнего пояса.
Признаки нулевого стержня
Нулевым называют стержень, в котором усилие равно нулю. Выделяют ряд частных случаев, в которых гарантированно встречается нулевой стержень.
- Равновесие ненагруженного узла, состоящего из двух стержней, возможно только в том случае, если оба стержня нулевые.
- В ненагруженном узле из трёх стержней одиночный (не лежащий на одной прямой с остальными двумя) стержень будет нулевым.

Рисунок 7
- В трехстержневом узле без нагрузки усилие в одиночном стержне будет равно по модулю и обратно по направлению приложенной нагрузке. При этом усилия в стержнях, лежащих на одной прямой, будут равны друг другу, и определятся расчётом N(3) = -P, N(1) = N(2).
- Трехстержневой узел с одиночным стержнем и нагрузкой, приложенной в произвольном направлении. Нагрузка P раскладывается на составляющие P’ и P» по правилу треугольника параллельно осям элементов. Тогда N(1) = N(2) + P’, N(3) = -P».
Рисунок 8
- В ненагруженном узле из четырёх стержней, оси которых направлены по двум прямым, усилия будут попарно равны N(1) = N(2), N(3) = N(4).
Пользуясь методом вырезания узлов и зная правила нулевого стержня, можно проводить проверку расчётов, проведённых другими методами.
com/embed/TrS89eJasr8″>Расчёт ферм на персональном компьютере
Современные вычислительные комплексы основаны на методе конечного элемента. С их помощью осуществляют расчёты ферм любого очертания и геометрической сложности. Профессиональные программные пакеты Stark ES, SCAD Office, ПК Лира обладают широким функционалом и, к сожалению, высокой стоимостью, а также требуют глубокого понимания теории упругости и строительной механики. Для учебных целей и подойдут бесплатные аналоги, например Полюс 2.1.1.
В Полюсе можно рассчитывать плоские статически определимые и неопределимые стержневые конструкции (балки, фермы, рамы) на силовое воздействие, определять перемещения и температурное воздействие. Перед нами эпюра продольных усилий для фермы, изображённой на рис. 2. Ординаты графика совпадают с полученными вручную результатами.
Рисунок 9
Порядок работы в программе Полюс
- На панели инструментов (слева) выбираем элемент «опора».
 Размещаем помещаем элементы на свободное поле кликом левой кнопки мыши. Чтобы указать точные координаты опор, переходим в режим редактирования, нажав на значок курсора на панели инструментов.
Размещаем помещаем элементы на свободное поле кликом левой кнопки мыши. Чтобы указать точные координаты опор, переходим в режим редактирования, нажав на значок курсора на панели инструментов. - Двойной клик по опоре. Во всплывающем окне «свойства узла» задаём точные координаты в метрах. Положительное направление осей координат — вправо и вверх соответственно. Если узел не будет использоваться в качестве опоры, установите флажок «не связан с землёй». Здесь же можно задать приходящие в опору нагрузки в виде точечной силы или момента, а также перемещения. Правило знаков такое же. Удобно разместить крайнюю левую опору в начале координат (точка 0, 0).
- Далее размещаем узлы фермы. Выбираем элемент «свободный узел», кликаем по свободному полю, точные координаты прописываем для каждого узла в отдельности.
- На панели инструментов выбираем «стержень». Кликаем на начальном узле, отпускаем кнопку мышки. Затем кликаем на конечном узле. По умолчанию стержень имеет шарниры на двух концах и единичную жёсткость.
 Переходим в режим редактирования, двойным кликом по стержню открываем всплывающее окно, при необходимости изменяем граничные условия стержня (жёсткая связь, шарнир, подвижный шарнир для опорного конца) и его характеристики.
Переходим в режим редактирования, двойным кликом по стержню открываем всплывающее окно, при необходимости изменяем граничные условия стержня (жёсткая связь, шарнир, подвижный шарнир для опорного конца) и его характеристики. - Для загружения ферм используем инструмент «сила», нагрузка прикладывается в узлах. Для сил, прикладываемых не строго вертикально или горизонтально, устанавливаем параметр «под углом», после чего вводим угол наклона к горизонтали. Альтернативно можно сразу ввести значение проекций силы на ортогональные оси.
- Программа считает результат автоматически. На панели задач (вверху) можно переключать режимы отображения внутренних усилий (M, Q, N), а также опорных реакций (R). Результатом будет эпюра внутренних усилий в заданной конструкции.
В качестве примера рассчитаем сложную раскосную ферму, рассмотренную в методе моментной точки (рис. 6). Примем размеры и нагрузки: d = 3м, h = 6м, P = 100Н. По выведенной ранее формуле значение усилия в верхнем поясе фермы будет равно:
O(7−9) = -8d∙P/h = -8∙3м∙100Н/6м = -400 Н (сжатие)
Эпюра продольных усилий, полученная в Полюсе:
Рисунок 10
Значения совпадают, конструкция смоделирована верно.
Список литературы
- Дарков А. В., Шапошников Н. Н. — Строительная механика: учебник для строительных специализированных вузов — М.: Высшая школа, 1986.
- Рабинович И. М. — Основы строительной механики стержневых систем — М.: 1960.
расчет статически определимой фермы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
В. К. Манжосов
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ ФЕРМЫ
Методические указания
Ульяновск
2010
УДК 624.04(076) ББК 38.121я7
М 23
Рецензент канд. техн. наук, доцент А. Н. Черный
Одобрено секцией методических пособий научно-методического совета университета.
Манжосов, В. К.
М23 Расчет статически определимой фермы : методические указания. – Ульяновск : УлГТУ, 2010. – 36 с.
Составлены в соответствии с учебными программами по дисциплине «Строительная механика» для направления «Строительство». Методические указания предназначены для выполнения расчетно-проектировочных и контрольных заданий, предусмотренных рабочими программами по дисциплине.
Работа подготовлена на кафедре теоретической и прикладной механики.
УДК 624.04(076) ББК 38.121я7
Учебное издание МАНЖОСОВ Владимир Кузьмич
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ ФЕРМЫ
Методические указания
Редактор М. В. Теленкова
Подписано в печать 01.102010. Формат 60×84/16. Усл. печ. л. 2,09. Тираж 100 экз. Заказ 1038.
Ульяновский государственный технический университет, 432027, Ульяновск, Сев. Венец, 32.
Типография УлГТУ, 432027, Сев. Венец, 32
Манжосов В. К., 2010.Оформление. УлГТУ, 2010
2
СОДЕРЖАНИЕ |
|
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ ФЕРМЫ..………………… | 4 |
1. | 4 |
2.Расчет статически определимой фермы с одноярусными шпрен-
гелями……………………………………………………………….. 6
2.1. Задание для расчета статически определимой фермы……… | 6 |
2.2. Кинематический анализ……………………………………… | 6 |
2.3. Определение усилий в стержнях заданной панели…………. | 6 |
2.3.1. Определение усилий в стержнях панели основной | 6 |
фермы………………………………………………………….. | |
2.3.2. Определение усилий в стержнях шпренгеля………… | 8 |
2.3.3. Определение усилий в стержнях заданной панели…. | 10 |
2.4. Построение линий влияния усилий для стержней панели… | 10 |
2.4.1. Построение линий влияния усилий для стержней | 10 |
заданной панели основной фермы…………………………… |
2. 4.2.Линии влияния продольных сил в шпренгельных стержнях……………………………………………………… 13
4.2.Линии влияния продольных сил в шпренгельных стержнях……………………………………………………… 13
2.4.3.Линии влияния усилий в стержнях 3-й панели на уча-
|
|
|
стках (1 | 10 ), ( 9 2 ), ( 2 10 )……………………………… 16 | |
2.5.Определение усилий в стержнях 3-й панели по линиям
влияния и сопоставление с аналитическими данными………….. 17
3.Расчет статически определимой фермы с двухъярусными шпрен-
гелями …………………………………………………………….. 19
3.1. Задание для расчета статически определимой фермы……… | 19 |
3.2. Кинематический анализ……………………………………… | 20 |
3.3. Определение усилий в стержнях заданной панели…………. | 20 |
3.3.1. Определение усилий в стержнях панели основной |
|
фермы…………………………………………………………. | 20 |
3.3.2. Определение усилий в стержнях шпренгеля………… | 22 |
3.3.3. Определение усилий в стержнях заданной панели…. | 24 |
3.4. Построение линий влияния усилий для стержней панели… | 24 |
3.4.1. Построение линий влияния усилий для стержней |
|
заданной панели основной фермы…………………………… | 25 |
3.4.2.Линии влияния продольных сил в шпренгельных стержнях……………………………………………………… 28
3.4.3.Линии влияния усилий в стержнях 4-й панели на
участках |
| (11 |
|
|
|
|
| 5 ), |
(12 1 ), | 2 ), | ( 2 12 ), | ( 2 | 1 ), | (1 |
( 5 4 ), (1 4 )…………………………………………………. | 31 |
|
|
3.5.Определение усилий в стержнях 4-й панели по линиям
влияния и сопоставление с аналитическими данными…………. | 32 |
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ…………..…………… | 34 |
СХЕМЫ РАСЧЕТНЫХ ЗАДАНИЙ……………………………………… | 35 |
3 |
|
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ ФЕРМЫ 1. Основные понятия
Плоские фермы представляют собой стержневые системы, состоящие из отдельных, обычно прямолинейных, стержней, соединенных между собой в узлах фермы. В большинстве случаев соединения стержней фермы в узлах являются жесткими (с помощью сварки, заклепок, болтов и других скреплений). Точный расчет фермы с такими узлами достаточно сложен, так как такая ферма является много раз статически неопределимой системой.
Однако, если нагрузка фермы приложена в узлах, то расчет фермы можно значительно упростить, условно заменив жесткие узлы фермы шарнирными соединениями. Точные расчеты показывают, что такая замена допустима, так как при сосредоточенных нагрузках, приложенных в узлах, усилия, возникающие в шарнирной ферме, мало отличаются от усилий в ферме с жесткими узлами.
Точные расчеты показывают, что такая замена допустима, так как при сосредоточенных нагрузках, приложенных в узлах, усилия, возникающие в шарнирной ферме, мало отличаются от усилий в ферме с жесткими узлами.
В данной работе изложена последовательность расчета плоской статически определимой, геометрически неизменяемой шпренгельной фермы.
Статически определимой является ферма, когда для определения усилий в ее стержнях достаточно уравнений статического равновесия.
Геометрически неизменяемой является ферма, у которой перемещение ее точек возможно лишь в связи с деформацией ее элементов. Простейшей статически определимой, геометрически неизменяемой системой является шарнирный треугольник (рис. 1.1, а).
а) б)
Рис. 1.1. Статически определимая, геометрически неизменяемая стержневая система
Более сложная статически определимая, геометрически неизменяемая система может быть образована путем последовательного присоединения узлов, причем каждого двумя стержнями, не лежащими на одной прямой (рис. 1.1, б).
1.1, б).
Зависимость между числом узлов K и числом стержней С для получения простейшей плоской статически определимой и геометрически неизменяемой фермы может быть определена по формуле
C 2K 3 .
Если число стержней C 2K 3, то это показывает, что ферма в своем составе не имеет минимального количества стержней, необходимого для образования геометрически неизменяемой системы.
По конструктивным соображениям раскосы фермы удобно располагать
так, чтобы они составляли со стойками и поясами углы, близкие к 45o . При увеличении высоты фермы увеличивается длина панелей. Устройство больших
4
панелей вызывает увеличение массы технологической части сооружения на этих панелях.
Задача увеличения высоты фермы может быть рациональна решена при введении в состав каждой панели дополнительных двухопорных ферм – шпренгелей (рис. 1.2, б, в), опирающихся на узлы основной фермы (рис. 1.2, а).
а) Схема фермы без шпренгелей (основная ферма)
б) Схема фермы с одноярусными шпренгелями
в) Схема фермы с двухъярусными шпренгелями Рис. 1.2. Схемы статически определимых ферм
1.2. Схемы статически определимых ферм
Различают одноярусные шпренгели (рис. 1.2, б), передающие нагрузку в узлы грузового пояса, и двухъярусные шпренгели (рис. 1.2, в), передающие нагрузку в узлы противоположного пояса.
Элементы (стержни) ферм, в состав которых входят одноярусные шпренгели, делят на следующие три категории:
1)элементы, принадлежащие только основной ферме. Усилия в этих стержнях определяются расчетом основной фермы; эти усилия не меняются при включении в ферму шпренгелей;
2)элементы, принадлежащие только шпренгелям. Усилия в них могут быть найдены из уравнений равновесия, составляемых для отдельных частей шпренгеля, который при этом можно рассматривать как самостоятельную двухопорную ферму;
3)элементы, принадлежащие одновременно основной ферме и шпренгелю. Усилие в каждом из них равно сумме двух усилий, одно из которых возникает в элементе основной фермы, а другое – в слившемся с ним элементе шпренгеля.
5
Элементы (стержни) ферм, в состав которых входят двухъярусные шпренгели, делятся на четыре категории: из них первые три те же, что и для ферм с одноярусными шпренгелями. Элементами четвертой категории являются те из элементов основной фермы (первой категории), линии влияния для которых имеют различный вид при перемещении единичной силы по верхнему грузовому поясу или по нижнему грузовому поясу.
Элементами четвертой категории являются те из элементов основной фермы (первой категории), линии влияния для которых имеют различный вид при перемещении единичной силы по верхнему грузовому поясу или по нижнему грузовому поясу.
2.Расчет статически определимой фермы с одноярусными шпренгелями
2.1. Задание для расчета статически определимой фермы
Для заданной статически определимой фермы, нагруженной силами Р в узлах нижнего грузового пояса (рис. 2.1), требуется:
1.Произвести кинематический анализ.
2.Определить усилия в стержнях заданной панели (третьей панели).
3.Построить линии влияния усилий для стержней заданной панели.
4.Определить усилия по линиям влияния и сопоставить их с усилиями, найденными аналитически.
Рис. 2.1. Расчетная схема фермы
2.2.Кинематический анализ
Цель кинематического анализа – выяснить геометрическую неизменяемость сооружения. Геометрическая неизменяемость сооружения обеспечивается в том случае, если степень свободы сооружения равна нулю.
Определим степень свободы фермы w по формуле
w 2K C C0 ,
где K число узлов фермы, C число стержней фермы, C0 число опорных
стержней.
Так как К = 26, С = 49, C0 = 3, то степень свободы фермы w равна
w 2 26 49 3 = 0.
Ферма является статически определимой и геометрически неизменяемой.
2.3. Определение усилий в стержнях заданной панели
2.3.1. Определение усилий в стержнях панели основной фермы
Отбросим шпренгельные элементы и образуем основную ферму (рис. 2.2). Нагрузку, приложенную к шпренгелям, распределим в узлы основной фермы.
6
Рис. 2.2. Расчетная схема фермы без шпренгельных элементов
Врезультате в узлах 8, 9, 10, 11 и 12 действуют силы по 2P , а на опоры А
иВ действуют силы по 0,5P . Из уравнений равновесия в виде равенства нулю
суммы моментов сил относительно узла А: M A (Pi ) 0 , следует
(RB 0,5P) 6d 2P(d 2d 3d 4d 5d) 0 ,
RB 6d 0,5P 6d 2P 15d 0 , RB 5,5P .
Из уравнений равновесия в виде равенства нулю суммы моментов сил относительно узла В: M B (Pi ) 0 , следует
(RA 0,5P) 6d 2P(d 2d 3d 4d 5d) 0RA 6d 0,5P 6d 2P 15d 0 , RA 5,5P .
Сечением I рассечем стержни 3-4, 3-10, 9-10 и отбросим правую от сечения часть фермы (рис. 2.3).
Рис. 2.3. Расчетная схема левой части основной фермы
Из уравнения равновесия в виде равенства нулю суммы моментов сил относительно узла 10: M10 (Pi ) 0 , следует
(N3 4 )oc d (RA 0,5P) 3d 2P 2d 2P d 0 ,
откуда
(N3 4 )oc (RA 0,5P) 3 2P 2 2P 15P 4P 2P 9P .
Из уравнения равновесия в виде равенства нулю суммы моментов сил относительно узла 3: M3 (Pi ) 0 , следует
(N9 10 )oc d (RA 0,5P) 2d 2P d 0 ,
7
откуда
(N9 10 )oc (RA 0,5P) 2 2P 8P .
Для левой части фермы (рис. 2.3) из условия равновесия в виде равенства нулю суммы проекций сил на ось y : Piy 0, следует, что
(RA 0,5P) 2P 2P (N3 10 )oc cos 45o 0 .
Из данного равенства
(N | 3 10 | )oc | (RA 0,5P) 2P 2P |
| P | = | 2P | 2 P. |
|
| cos 45o |
| 2 / 2 | 2 |
| ||
Вырежем узел 9 и рассмотрим силы, образующие в этом узле систему сходящихся сил (рис. 2.4).
Рис. 2.4. Схема сил, сходящихся в узле 9 основной фермы
Из условия равновесия узла 9 в виде равенства нулю суммы проекций сил на ось y : Piy 0, следует, что
(N9 3 )oc 2P 0 , | (N9 3 )oc 2P . |
Вырежем узел 4 и рассмотрим силы, образующие в этом узле систему сходящихся сил (рис. 2.5).
Рис. 2.5. Схема сил, сходящихся в узле 4 основной фермы
Из условия равновесия узла 4 в виде равенства нулю суммы проекций сил на ось y : Piy 0, следует, что
(N4 10 )oc 0 .
Последнее равенство означает, что стержень (4-10) не загружен.
2.3.2. Определение усилий в стержнях шпренгеля
Вернемся теперь к исходной расчетной схеме (рис.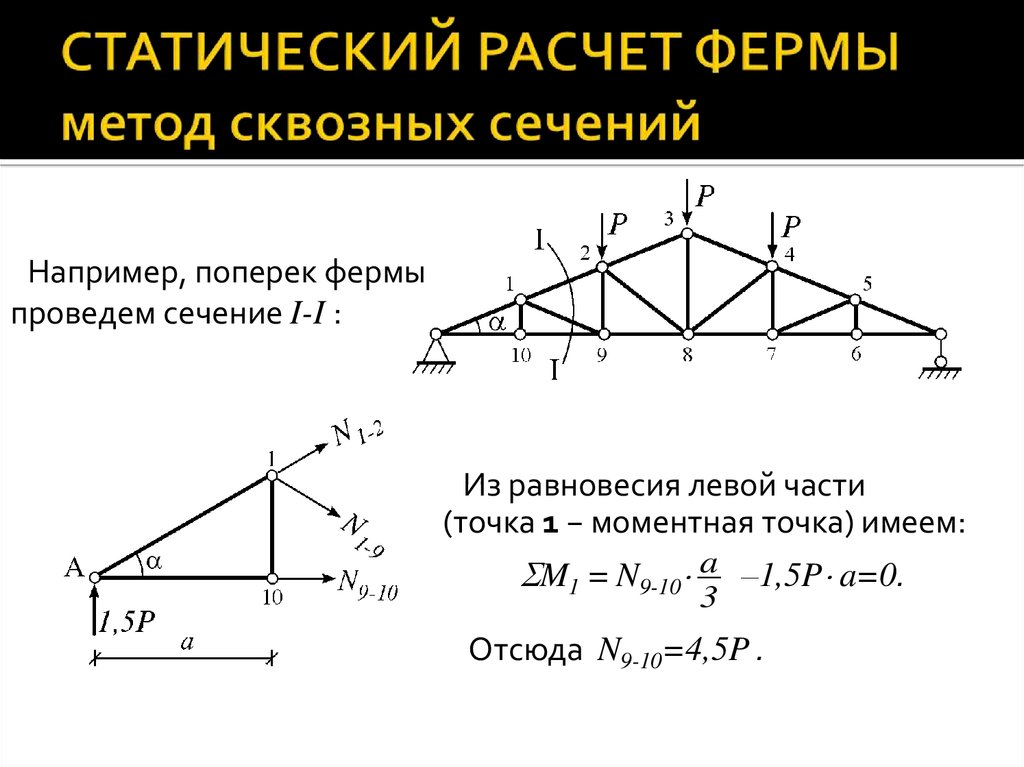 2.1). Изобразим шпренгель третьей панели на рис. 2.6 в виде двухопорной фермы.
2.1). Изобразим шпренгель третьей панели на рис. 2.6 в виде двухопорной фермы.
Из условия равновесия шпренгеля реакции в опорах
R9 0,5P ; | R10 0,5P . |
8
Рис. 2.6. Расчетная схема шпренгеля | Рис. 2.7. Схема сил, сходящихся в узле 9 |
третьей панели | шпренгеля |
Рассмотрим равновесие сил в узле 9 шпренгеля (рис. 2.7).
Из уравнения равновесия в виде равенства нулю суммы проекций сил на ось y : Piy 0, следует, что
|
|
|
|
|
|
| R (N | )ш sin 45o | 0 , |
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
| 9 |
|
|
| 9 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
откуда |
|
|
| (N |
| )ш |
|
| R9 |
|
| P |
|
|
| 2 |
| P . |
| |||||||
|
|
|
| sin 45o | 2 |
|
| 2 |
| |||||||||||||||||
|
|
|
|
|
| 9 1 |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
Из уравнения равновесия в виде равенства нулю суммы проекций сил на | ||||||||||||||||||||||||||
ось x : Pix 0 , | следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
| (N |
| )ш (N |
| )ш cos 45o 0 , |
|
| |||||||||||||||
|
|
|
|
|
|
| 9 2 |
|
|
|
| 9 1 |
|
|
|
|
|
|
|
|
|
|
|
| ||
откуда |
| (N | )ш | (N |
| )ш |
| cos 45o | 2 |
| P |
| 2 | 0,5P . | ||||||||||||
|
|
|
|
|
|
| ||||||||||||||||||||
|
|
| 9 2 |
|
|
|
| 9 1 |
|
|
|
|
|
| 2 |
|
|
|
|
| 2 |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Из условия симметрии шпренгельного элемента и его нагружения следует, | ||||||||||||||||||||||||||
что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(N | )ш (N |
| )ш |
| 2 |
|
| P , |
| (N |
| )ш | (N |
| )ш 0,5P . | |||||||||||
|
|
|
|
|
|
| ||||||||||||||||||||
10 1 |
|
| 9 1 |
|
|
| 2 |
|
|
|
|
|
| 10 2 |
|
|
| 9 2 | ||||||||
Вырежем узел 2 и рассмотрим силы, образующие в этом узле систему сходящихся сил (рис. 2.8).
Рис. 2.8. Схема сил, сходящихся в узле 2 фермы
Из условия равновесия сил в узле 2 в виде равенства нулю суммы проекций сил на ось y : Piy 0, следует
|
|
|
| (N | )ш P 0 , (N |
| )ш | P . |
|
| |||
|
|
|
| 2 | 1 |
| 2 | 1 |
|
|
|
| |
Таким образом, в стержнях шпренгеля 3-й панели |
|
| |||||||||||
(N | )ш | 2 | P 0,707P , (N | )ш 0,5P ; |
| (N |
| )ш (N | )ш 0,707P ; | ||||
|
|
| |||||||||||
| 9 1 | 2 |
|
|
|
| 9 2 |
| 10 1 |
| 9 1 | ||
|
| (N | )ш | (N |
| )ш 0,5P ; |
| (N |
| )ш | P . |
| |
|
|
|
|
|
|
| |||||||
|
|
| 10 2 |
| 9 2 |
| 2 | 1 |
|
| |||
9
2.3.3. Определение усилий в стержнях заданной панели
Рис. 2.9. Схема для определения сил в стержнях третьей панели
Усилия в стержнях заданной панели (рис. 2.9), совмещенных со стержнями шпренгеля, вычисляются суммированием усилий в стержнях основной фермы и усилий в соответствующих стержнях шпренгеля:
Ni Niос Niш ,
где N i – усилие в i-м стержне заданной фермы, Nioc – усилие в i-м стержне основ-
ной фермы, Niш – усилие в стержне шпренгеля, совпадающим с i-м стержнем
основной фермы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
| Для третьей панели получим следующие | значения | усилий в | стержнях | |||||||||||||||||||
(рис. 2.9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
| N | 3 4 | N oc |
| 9P, | N | 9 3 | N oc 2P , | N |
|
| N oc | 2P, | N | N ш P, | |||||||||
|
|
| 3 4 |
|
|
|
|
| 9 3 |
| 3 1 | 3 10 |
|
|
|
| 2 | 1 | 2 1 | ||||||
N | 4 10 | N oc | 0, | N |
| N ш | 0,707P, | N |
| N oc |
| N ш | 8P 0,5P 8,5P ; | ||||||||||||
|
| 4 10 |
|
|
| 9 1 | 9 1 |
|
| 9 2 | 9 10 |
| 9 2 |
|
|
| |||||||||
N |
|
| N oc |
| N ш |
|
| 8P 0,5P 8,5P ; | N |
|
| N oc N ш |
|
| 2P 0,707P 0,707P . | ||||||||||
| 10 2 | 10 9 |
| 10 2 |
|
|
|
|
| 1 10 |
| 3 10 |
| 1 10 |
|
|
|
|
| ||||||
2.4. Построение линий влияния усилий для стержней панели.
Линии влияния усилий в стержнях заданной панели строятся при перемещении единичной силы по узлам нижнего грузового пояса фермы, схема которой приведена на рис. 2.10.
Рис. 2.10. Расчетная схема фермы
2.4.1. Построение линий влияния усилий для стержней заданной панели основной фермы
Вначале построим линии влияния в стержнях для третьей панели основной фермы, схема которой без шпренгельных элементов изображена на рис. 2.11.
Рис. 2.11. Расчетная схема фермы без шпренгельных элементов
10
Статически определимые фермы — Разные темы по физике (Физика)
Основные понятия и определения.
Ферма — такая стержневая система, которая сохраняет геометрическую неизменяемость в случае если во всех местах соединения ее стержней (узлах фермы) врезать шарниры (рис.1). Стержни, представляющие собой верхнюю часть контура фермы, называют верхним поясом фермы, нижнюю часть — нижним поясом фермы. Расстояние между двумя соседними узлами любого из поясов фермы называется панелью фермы. Вертикальные стержни в ферме называют стойками, наклонные — раскосами. Совокупность раскосов и стоек образует решетку фермы.
В зависимости от конфигурации решетки различают фермы различных типов. Наиболее распространенными являются раскосные фермы (рис.2) и фермы с треугольной решеткой (рис.3). Раскосы, идущие вверх от опор к середине фермы, называют восходящими раскосами (рис.1), идущие наоборот — нисходящими раскосами (рис.2). Фермы, усиленные дополнительными стержнями (шпренгелями), называют шпренгельными фермами (рис. 4).
4).
Фермы, как правило, проектируют таким образом, чтобы основная нагрузка на них передавалась через узлы верхнего или нижнего пояса. Наличие шпренгелей позволяет увеличить количество узлов в этом поясе, что может потребоваться для облегчения конструкций, с помощью которых внешняя нагрузка передается на узлы фермы или, например, для уменьшения ширины плит перекрытий, опирающихся на стропильные фермы здания. (рис.5).
В зависимости от характера опорных закреплений различают балочные фермы (рис.6), консольные фермы (рис.7), консольно-балочные фермы (рис.8) и арочные фермы (рис.9). Кроме того, отдельно рассматриваются различные висячие системы (рис.10) и комбинированные системы (рис.11).
Если нагрузка на узлы верхнего или нижнего пояса фермы подвижная, например от действия движущегося подвижного состава в фермах пролетных строений мостов, то этот пояс фермы называют ездовой линией или проезжим поясом.
В качестве расчетной схемы фермы применяют шарнирную схему, в которой все узлы фермы считаются идеальными шарнирами.
Фермы используются в качестве пролетных строений мостов, стропильных конструкций зданий, опор линий элекропередач, радио- и телемачт, каркасов зданий, а также в различных машиностроительных конструкциях, например, в качестве стрел подъемных кранов.
Статическая работа ферм.
Фермы часто используются для перекрытия пролетов, т.е. имеют такое же назначение, что и балки сплошного сечения.
Известно, что при изгибе балки нормальные напряжения в ее поперечных сечениях достигают максимальных значений в верхних и нижних точках сечения. Желание использовать материал балки наиболее экономичным образом заставляет сосредотачивать большую часть материала в наиболее напряженных зонах, что достигается применением балок двутаврового поперечного сечения (рис.12). При увеличении пролета и нагрузок высоту балки приходится увеличивать. Следовательно, количество материала в стенке, где напряжения малы, будет расти.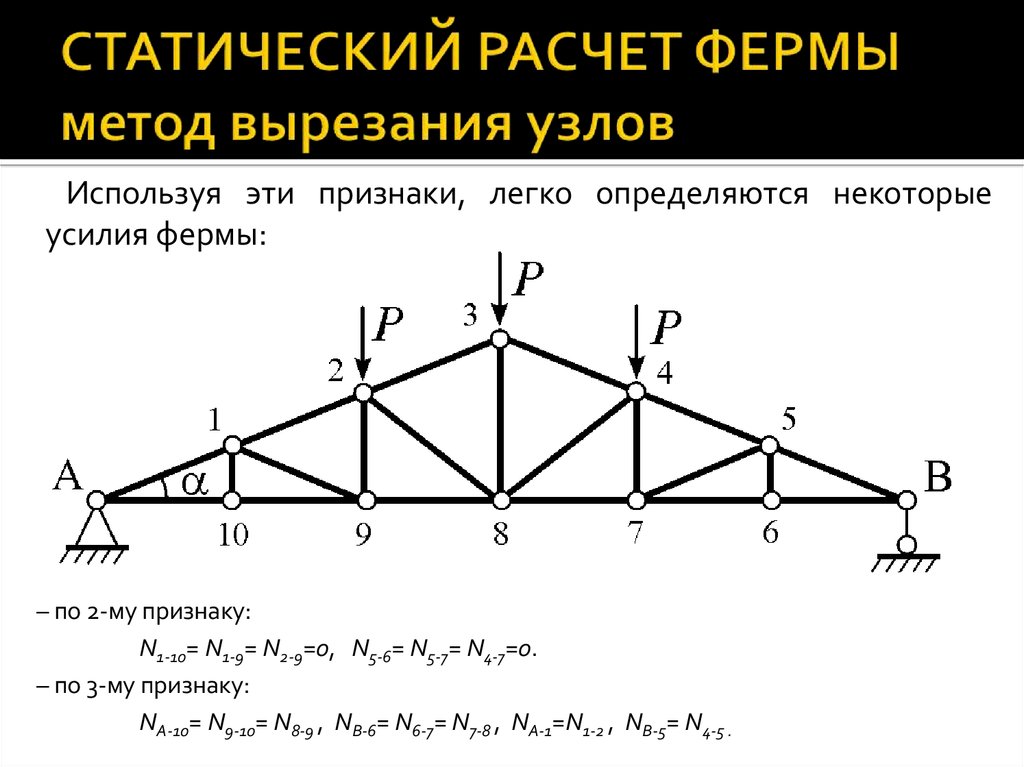 Это приведет не только к перерасходу материала в малозагруженной зоне, но и значительно увеличит собственный вес конструкции. Поэтому для экономии материала и облегчения конструкции в вертикальной стенке устраивают вырезы (рис.13). С дальнейшим ростом пролета и нагрузок высота сечения конструкции еще увеличивается, и стенка двутавра постепенно переходит в систему стоек. Для того, чтобы полученная конструкция сохраняла геометрическую неизменяемость, т.е. не “сложилась” при действии горизонтальных нагрузок, к системе стоек добавляют систему раскосов, в результате чего и образуется решетка фермы (рис.14).
Это приведет не только к перерасходу материала в малозагруженной зоне, но и значительно увеличит собственный вес конструкции. Поэтому для экономии материала и облегчения конструкции в вертикальной стенке устраивают вырезы (рис.13). С дальнейшим ростом пролета и нагрузок высота сечения конструкции еще увеличивается, и стенка двутавра постепенно переходит в систему стоек. Для того, чтобы полученная конструкция сохраняла геометрическую неизменяемость, т.е. не “сложилась” при действии горизонтальных нагрузок, к системе стоек добавляют систему раскосов, в результате чего и образуется решетка фермы (рис.14).
Таким образом, фермы могут быть использованы для перекрытия больших пролетов при действии высоких нагрузок, когда использование балок сплошного сечения оказывается невыгодным или невозможным.
Как и при изгибе балки на двух опорах под действием нагрузки, направленной вниз, стержни верхнего пояса балочной фермы будут сжатыми, а нижнего — растянутыми. В консольной ферме (рис. 7) ситуация будет обратной.
7) ситуация будет обратной.
Узлы фермы, как правило, конструктивно выполняются жесткими. Однако, как показал опыт расчетов, напряжения в стержнях ферм, определенные с учетом жесткости узлов, и напряжения, определенные по шарнирной схеме, обычно отличаются не более, чем на несколько процентов. Поскольку выполнять расчет во втором случае значительно легче, жесткостью узлов фермы пренебрегают и расчет ведут по шарнирной схеме. Иными словами, при расчете фермы все ее узлы считают идеальными шарнирами.
Если все нагрузки на ферму приложены исключительно к узлам, а стержни ферм являются прямыми, то в стержнях ферм действуют только продольные усилия, а изгибающие моменты и перерезывающие усилия отсутствуют. Действительно, вырежем мысленно любой стержень из фермы, заменив действие остальных стержней на него усилиями, передаваемыми через шарниры (рис.15). Поскольку других нагрузок на стержень нет, равнодействующие этих сил должны быть направлены по оси стержня. Если бы это было не так, стержень не мог бы находиться в равновесии, в чем легко убедиться, составив уравнение моментов относительно любого из шарниров.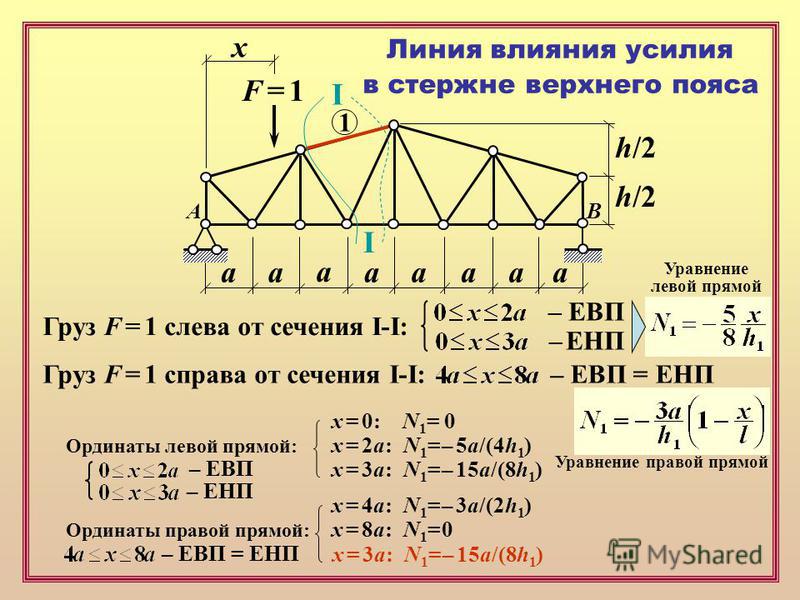 Очевидно, единственным усилием, которое в этом случае будет возникать в стержне, будет постоянное по его длине продольное усилие.
Очевидно, единственным усилием, которое в этом случае будет возникать в стержне, будет постоянное по его длине продольное усилие.
Геометрическая неизменяемость ферм.
Для обеспечения геометрической неизменяемости необходимо, во-первых, чтобы связей, наложенных на перемещение узлов фермы было достаточно, во-вторых, они были правильно размещены. Следовательно, исследование геометрической неизменяемости фермы состоит из двух шагов: проверки достаточности числа связей и анализе правильности их размещения (структурном анализе фермы).
Как обычно, при анализе геометрической неизменяемости смещения, вызванные деформированием стержней в расчет не берутся. Иными словами, при анализе геометрической неизменяемости ферм, как и любых других стержневых систем, будем считать стержни абсолютно жесткими.
Каждый узел плоской фермы имеет две степени свободы, т.е. имеет возможность линейного смещения, например, в вертикальном и горизонтальном направлениях. Следовательно, минимальное количество связей, необходимых для закрепления узлов фермы от смещений, должно равняться удвоенному числу узлов. Часть из этих связей должна обеспечивать закрепление фермы относительно основания. Таким образом, минимальное число стержней в ферме, необходимое для обепечения ее геометрической неизменяемости определяется по формуле:
Часть из этих связей должна обеспечивать закрепление фермы относительно основания. Таким образом, минимальное число стержней в ферме, необходимое для обепечения ее геометрической неизменяемости определяется по формуле:
где -число стержней в ферме, — число узлов , а -число опорных связей.
Условие (1) одновременно является условием статической определимости фермы. Действительно, для каждого узла можно составить два уравнения равновесия- условия равенства нулю проекций на вертикальную и горизонтальную оси всех действующих на узел внешних сил и сил, действующих со стороны стержней и реакций опор. Неизвестными же являются продольные усилия в каждом стержне и реакции в опорах. Записав все эти уравнений, получим систему уравнений, которую в матричной форме можно записать в виде:
где Х — вектор неизвестных усилий в стержнях и опорных связях, В — вектор проекций внешних нагрузок на узлы, А-матрица системы.
Для того, чтобы система (2) была замкнутой, необходимо чтобы число уравнений совпадало с числом неизвестных, т. е. выполнялось условие (1).
е. выполнялось условие (1).
Если количество стержней в ферме будет больше, чем требуется согласно (1), то ферма будет статически неопределимой, если меньше — то геометрически изменяемой.
При этом, важно отметить, что условие (1) является необходимым, но не достаточным для обеспечения геометрической неизменяемости. Как уже упоминалось, кроме обеспечения необходимого числа связей, требуется их правильное размещение.
Систему, в которой невозможны взаимные смещения узлов, в предположении, что все стержни абсолютно жесткие, называют жестким диском. В шарнирном треугольнике (например, ABC на рис.16) взаимное смещение узлов будет невозможным, следовательно он является жестким диском. Присоединение к такому треугольнику еще одного узла двумя не лежащими на одной прямой связями приведет к образованию системы, в которой также взаимные смещения узлов будут невозможны. Если продолжить этот процесс, то полученная система также будет жеским диском. Примером жесткого диска является простейшая ферма, т. е. ферма, состоящая из шарнирных треугольников (рис.16). Взаимные смещения узлов в такой фермы невозможны. Остается только позаботиться о прикреплении полученной простейшей фермы к основанию.
е. ферма, состоящая из шарнирных треугольников (рис.16). Взаимные смещения узлов в такой фермы невозможны. Остается только позаботиться о прикреплении полученной простейшей фермы к основанию.
Для того, чтобы обеспечить неподвижность простейшей фермы относительно основания, необходимы как минимум три опорных связи, линии действия которых не параллельны и не пересекаются в одной точке.
Рассмотрим в качестве примера ферму, изображенную на рис.1. Очевидно, она относится к простейшим фермам. В ней , ,. Равенство (1) выполняется: 25=2×14-3=25. Линии действия трех опорных связей (опорных реакций на рис.1) не параллельны и не пересекаются в одной точке, следовательно ферма геометрически неизменяема.
Теперь выполним перестановку опорных связей. Отбросим на левой опоре одну связь, сделав неподвижную опору катковой, но добавим еще одну катковую опору в центре пролета фермы (рис.17).
В результате, количество опорных связей не изменилось, а осталось равным трем, т.е. равенство (1) осталось справедливым. Однако линии действия опорных связей стали параллельными — направленными вертикально вверх. В результате система получила возможность смещения в горизонтальном направлении, т.е. стала геометрически изменяемой.
Однако линии действия опорных связей стали параллельными — направленными вертикально вверх. В результате система получила возможность смещения в горизонтальном направлении, т.е. стала геометрически изменяемой.
Если же в ферме, изображенной на рис.1, выполнить перестановку стержней, как показано на рис.18, равенство (1) останется неизменным, но система окажется геометрически изменяемой за счет неправильного распределения связей. Это очевидно, т.к. шарнирами C, D, E и F образуется шарнирный квадрат, который при приложении малейшей нагрузки обращается в ромб.
Если ферма образована из двух жестких дисков, то для того, чтобы исключить взаимные смещения узлов в полученной системе, необходимо, чтобы они соединялись между собой как минимум тремя связями, линии действия которых не параллельны и не пересекаются в одной точке.
В ферме на рис.18 два жестких диска ABCD (он представляет собой простейшую ферму) и FEGH (ферма, образованная из простейшей добавлением одной “лишней” связи) соединются между собой только двумя связями DF и CE, что и приводит к геометрической изменяемости фермы, в чем мы уже убедились.
Рассмотрим арочную ферму, изображенную на рис.9. Здесь , ,. Условие (1) выполняется: 18=11×2-4=18. Эта ферма также образована двумя жесткими дисками (простейшими фермами). Они соединяются между собой шарниром С, т.е., на первый взгляд, только двумя связями, т.к. шарнир препятствует взаимному смещению соединяемых им узлов в вертикальном и горизонтальном направлениях. Однако, поскольку опоры А и В неподвижны, взаимных горизонтальных смещений точек А и В быть не может. Значит, роль третьей связи играет основание. Поэтому рассматриваемая система геометрически неизменяема, а в обеих опорах возникнут горизонтальные распорные реакции.
Выполним перестановку связей в этой ферме. Сделаем одну из опор катковой, сняв таким образом ограничение на взаимные горизонтальные смещения точек А и В. Однако, добавим стержень, который возьмет на себя роль третьей связи, соединяющей простейшие фермы (рис.19). Равенство (1) при этом не нарушится: 19=11×2-3=19, система останется геометрически неизменяемой, а роль основания по восприятию горизонтального усилия перейдет введенному стержню, работающему в качестве затяжки.
В качестве еще одного примера рассмотрим ферму Шухова[1] (рис.20). В ней , ,. Условие (1) выполняется: 9=6×2-3=9.
Ферма образована двумя шарнирными треугольниками ABC и DEF, связанными между собой тремя связями- AF, BE, и DC, линии действия которых не параллельны и не пересекаются в одной точке. Прикрепление образованного в результате жесткого диска к основанию выполнено при помощи одной неподвижной и одной катковой опоры, т.е. также при помощи трех связей, линии действия которых не параллельны и не пересекаются в одной точке. Следовательно, ферма геометрически неизменяема.
В случаях, когда простым структурным анализом не удается доказать геометрическую неизменяемость фермы, приходится пользоваться более сложными методами. Одним из них является статический метод анализа геометрической неизменяемости ферм. Идея метода заключается в следующем. Для геометрически изменяемой фермы система уравнений (2) не должна иметь решений, следовательно матрица А должна быть особенной, т. е. ее определитель должен быть равен нулю. Как известно, если в однородной системе линейных алгебраических уравнений АХ=0 определитель матрицы А равен нулю, то система кроме тривиального решения Х=0 допускает и ненулевое решение. Поэтому, в стержнях статически определимой, но геометрически изменяемой фермы при нулевой нагрузке может возникнуть система самоуравновешенных сил.
е. ее определитель должен быть равен нулю. Как известно, если в однородной системе линейных алгебраических уравнений АХ=0 определитель матрицы А равен нулю, то система кроме тривиального решения Х=0 допускает и ненулевое решение. Поэтому, в стержнях статически определимой, но геометрически изменяемой фермы при нулевой нагрузке может возникнуть система самоуравновешенных сил.
Для того, чтобы доказать геометрическую неизменяемость фермы, необходимо доказать, что при отсутствии внешней нагрузки в ее стержнях не может возникнуть усилий. Если же оказывается, что при отсутствии нагрузки в стержнях фермы могут существовать ненулевые усилия, то это указывает на равенство определителя матрицы А нулю, а значит и на геометрическую изменяемость фермы.
При выполнении анализа подобного рода, как и при выполнении статического расчета фермы, оказываются полезными правила определения нулевых стержней. Нулевым стержнем называется стержень, в котором при рассматриваемой нагрузке усилие равно нулю. Приведем эти правила.
Приведем эти правила.
1. Если в незагруженном узле под углом соединяются два стержня, то оба стержня — нулевые (рис.21). В этом легко убедиться, составив уравнения проекций сил на оси, совпадающие с направлением стержней.
2. Если в незагруженном узле сходятся сходятся три стержня, причем два лежат на одной прямой, то третий стержень — нулевой (рис.22). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную двум стержням, лежащим на одной прямой.
3. Если к узлу, в котором сходятся два стержня, приложена сила, направление действия которой совпадает с одним из них, то второй стержень — нулевой (рис.23). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную линии действия внешней силы.
4. Если в узле сходятся три и более стержней, то те из них, о которых заранее известно, что они являются нулевыми, при определении остальных нулевых стержней и нахождении усилий в стержнях, очевидно, могут быть мысленно отброшены.
5. Если обо всех стержнях кроме одного, сходящихся в незагруженном узле, известно, что они нулевые, то и последний стержень тоже будет нулевым. В этом легко убедиться, составив уравнение проекций сил на ось, совпадающую с направлением этого стержня.
Если обо всех стержнях кроме одного, сходящихся в незагруженном узле, известно, что они нулевые, то и последний стержень тоже будет нулевым. В этом легко убедиться, составив уравнение проекций сил на ось, совпадающую с направлением этого стержня.
Рассмотрим в качестве примера ферму, изображенную на рис.24.
Для нее , ,. Условие (1) выполняется: 22=15×2-8=22. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т.е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отстутсвии внешней нагрузки.
Из рассмотрения узлов 5 и 7, согласно признаку 2 нулевых стержней следует, что стержени 3-5 и 7-6 — нулевые. Далее, из рассмотрения узла 3, согласно признакам 4 и 2 следует, что стержень 2-3 нулевой. Далее, из рассмотрения узла 2, согласно признакам 4 и 1 следует, что стержни 1-2 и 2-6 — нулевые. Далее, из рассмотрения узла 6, согласно признакам 4 и 2 следует, что стержень 3-6 нулевой, а значит, в соответствии с признаком 5, нулевым будет и стержень 6-8. Далее, из рассмотрения узла 3, согласно признаку 5 следует, что стержень 1-3 нулевой. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно стержни 8-10, 10-14, 14-15, 9-10, 11-12, 12-14, 10-12 и 12-15 тоже будут нулевыми. Рассмотрим теперь узел 8. В соответствии с признаками 4 и 1 стержень 7-8 будет нулевым. Далее, последовательно рассматривая узлы 7 и 5, пользуясь признаком 5, докажем, что стержни 5-7 и 4-5 — нулевые. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно 8-9, 9-11,11-13, тоже будут нулевыми. Итак, нам удалось доказать, что все стержни фермы при отсутствии нагрузки являются нулевыми. Следовательно, в этом случае в них не может возникнуть ненулевые усилия, а значит ферма геометрически неизменяема.
Далее, из рассмотрения узла 3, согласно признаку 5 следует, что стержень 1-3 нулевой. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно стержни 8-10, 10-14, 14-15, 9-10, 11-12, 12-14, 10-12 и 12-15 тоже будут нулевыми. Рассмотрим теперь узел 8. В соответствии с признаками 4 и 1 стержень 7-8 будет нулевым. Далее, последовательно рассматривая узлы 7 и 5, пользуясь признаком 5, докажем, что стержни 5-7 и 4-5 — нулевые. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно 8-9, 9-11,11-13, тоже будут нулевыми. Итак, нам удалось доказать, что все стержни фермы при отсутствии нагрузки являются нулевыми. Следовательно, в этом случае в них не может возникнуть ненулевые усилия, а значит ферма геометрически неизменяема.
Теперь рассмотрим ферму, изображенную на рис.25.
Для нее , ,. Условие (1) выполняется: 10=7×2-4=10. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т. е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отстутсвии внешней нагрузки.
е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отстутсвии внешней нагрузки.
Рассмотрим узел 1. Поскольку на него может действовать только вертикальная опорная реакция, в соответствии с признаком 3 нулевых стержней стержень 1-3 является нулевым. Из рассмотрения узла 7 тот же вывод можно сделать о стержне 5-7. Рассмотрим далее узел 3. На основании признаков 2 и 4 нулевых стержней можно заключить, что стержень 3-5 нулевой.
Предположим, что в стержне 1-2 возникло растягивающее усилие N1-2=N. Рассмотрим равновесие узла 2 (рис.26). Составим для него уравнения проекций действующих на узел усилий на вертикальную и горизонтальную оси: , , откуда следует, что , а . Рассмотрим далее равновесие ула 6 (рис.27). Из аналогичных уравнений равновесия, составленных для этого узла, получим:, . Отсюда следует, что , а .
Рассмотрим далее равновесие опорных узлов. Учитывая отсутствие усилий в стержнях 1-3, 3-5 и 3-7, из рассмотрения равновесия узлов 3 и 5 (из уравнения проекций сил на оси, совпадающие с направлением стержней 2-3 и 6-5) легко заключить, что и . Из уравнения равновесия проекций сил на вертикальную ось для узла 4 (рис.28), получим: , где V4-вертикальная опорная реакция. Отсюда следует, что .
Из уравнения равновесия проекций сил на вертикальную ось для узла 4 (рис.28), получим: , где V4-вертикальная опорная реакция. Отсюда следует, что .
Легко убедиться, что в каждой их двух других опор действует вертикальная реакция величиной N, направленная вверх. Составим для фермы уравнение проекций всех сил на вертикальную ось. Поскольку внешняя нагрузка отсутствует, в него будут входить только опорные реакции. Очевидно, их равнодействующая равна нулю, а значит система находится в равновесии.
Таким образом, мы доказали, что в стержнях фермы при отсутствии внешней нагрузки может иметься система самоурановешенных сил, что говорит о том, что ферма геометрически изменяема.
Если бы в процессе подобных рассуждений мы столкнулись с противоречием (например, невозможностью удовлетворить уравнениям равновесия) или доказали бы, что все стержни фермы — нулевые, то отсюда следовала бы невозможность существования такой системы усилий, а значит ферма была бы геометрически неизменяемой.
Статический расчет фермы
Статический расчет фермы заключается в определении реакций в ее опорах и нахождении усилий в ее стержнях.
Для статически определимых ферм для решения данной задачи, как известно, достаточно только уравнений равновесия. Составив для каждого узла по два уравнения равновесия проекций всех сил на вертикальную и горизонтальную оси, получим замкнутую систему уравнений (2), решив которую найдем усилия во всех стержнях фермы и реакции опор. Данный алгоритм может быть относительно просто реализован в виде программы для ЭВМ. Кроме того, статический расчет фермы может быть выполнен с применением программных комплексов на основе метода конечных элементов, о котором речь пойдет во второй части учебника.
В то же время, при расчете ферм с небольшим количеством стержней, а также при проверке результатов расчетов, полученных на ЭВМ, может потребоваться использование простейших приемов определения усилий в стержнях ферм. К ним относятся вырезание узлов и сечения.
Способ вырезания узлов уже использовался нами при статическом анализе геометрической неизменяемости фермы. Он заключается в мысленном вырезании узла фермы с заменой действия на него стержней соответствующими усилиями. Эти усилия связаны между собой и приложенной к стержню внешней нагрузкой (или опорными реакциями) посредством статических уравнений равновесия. Для любого узла можно составить два таких уравнения — равенства нулю суммы проекций всех сил, например, на вертикальную и горизонтальную оси. Очевидно, если в узле сходятся два стержня (например, рис.21 и рис.23), то из этих уравнений могут быть найдены усилия в обоих из них. Если узел соединяет три стержня, но усилие в одном из них уже найдено из рассмотрения равновесия другого узла или использованием способа сечений, то из этих двух уравнений могут быть найдены усилия в двух оставшихся стержнях.
Способ сечений состоит в мысленном рассечении фермы на две части и рассмотрении равновесия одной из них. При этом действие отбрасываемой части на рассматриваемую должно быть заменено усилиями в стержнях ферм. Если провести сечение таким образом, чтобы оно проходило через три стержня, то можно составить уравнения равновесия для рассматриваемой части фермы таким образом, чтобы найти усилия во всех трех стержнях.
Если провести сечение таким образом, чтобы оно проходило через три стержня, то можно составить уравнения равновесия для рассматриваемой части фермы таким образом, чтобы найти усилия во всех трех стержнях.
В качестве примера рассмотрим ферму, изображенную на рис.1. Для определения усилия в любом из ее раскосов, а также в любом стержне верхнего или нижнего пояса достаточно провести вертикальное сечение в соответствующей панели фермы и рассмотреть равновесие любой отсеченной части. Очевидно, выгоднее рассматриваить равновесие той части, для которой проще составить уравнение равновесия (рис.29).
Если составить уравнение равновесия моментов относительно точки А, то в это уравнение войдет только одно неизвестное усилие — усилие NНП в стержне нижнего пояса. Следовательно, это усилие может быть определено из этого уравнения. Если составить уравнение равновесия моментов относительно точки В, то в это уравнение также войдет только одно неизвестное усилие — усилие NВП в стержне верхнего пояса. Следовательно, это усилие может быть определено из этого уравнения. Если составить уравнение равновесия проекций всех сил на вертикальную ось, то в это уравнение войдет только одно неизвестное усилие — усилие в раскосе NР. Следовательно, это усилие может быть определено из этого уравнения. Для определения усилия в стойке сечение нужно выполнять так, чтобы оно проходило через нее (рис.30).
Следовательно, это усилие может быть определено из этого уравнения. Если составить уравнение равновесия проекций всех сил на вертикальную ось, то в это уравнение войдет только одно неизвестное усилие — усилие в раскосе NР. Следовательно, это усилие может быть определено из этого уравнения. Для определения усилия в стойке сечение нужно выполнять так, чтобы оно проходило через нее (рис.30).
Если составить уравнение равновесия проекций всех сил на вертикальную ось, то в это уравнение войдет только одно неизвестное усилие — усилие в стойке NС. Следовательно, это усилие может быть определено из этого уравнения.
Если в сечение попадает количество стержней превышающее три, то чаще всего приходится комбинировать способ сечений и способ вырезания узлов, определяя усилия в части из стержней в сечении из рассмотрения равновесия узлов или при выполнении других сечений.
Таким образом, усилие в любом стержне статически определимой фермы может быть определено в один или несколько шагов путем последовательных вырезаний узлов и/или рассмотрением равновесия отсеченных определенным образом частей фермы.
Очевидно, при использовании этих способов необходимо предварительное определение опорных реакций из уравнений равновесия фермы.
Пример расчета фермы на неподвижную нагрузку.
Выполним статический расчет фермы, изображенной на рис.31.
Для данной фермы , ,. Условие (1) выполняется: 17=10×2-3=17. Следовательно, необходимое условие статической неопределимости и геометрической неизменяемости фермы выполняется.
Теперь исследуем правильность расстановки связей в ферме. Данная ферма образована двумя жесткими дисками. Контур первого из них ограничен узлами 1,4,6,5,2. Действительно, жесткий диск образован тремя шарнирными треугольниками, к которым двумя стержнями, не лежащими на одной прямой, присоединен узел 5. Второй диск, контур которого ограничен узлами 6,8,7,10,9, также образован тремя шарнирными треугольниками, т.е. представляет собой простейшую ферму. Два диска соединены между собой тремя связями, линии действия которых не параллельны и не пересекаются в одной точке,- в узле 6 и стержнем 5-7. Таким образом, вся конструкция также представляет собой жесткий диск. Он прикреплен к основанию тремя связями, линии действия которых не параллельны и не пересекаются в одной точке. Следовательно, на основе структурного анализа можно сделать вывод, что данная ферма является геометрически неизменяемой.
Таким образом, вся конструкция также представляет собой жесткий диск. Он прикреплен к основанию тремя связями, линии действия которых не параллельны и не пересекаются в одной точке. Следовательно, на основе структурного анализа можно сделать вывод, что данная ферма является геометрически неизменяемой.
Определим опорные реакции в ферме. Горизонтальная нагрузка на систему отстутствует, следовательно горизонтальная реакция в левой опоре равна нулю . Поскольку данная ферма симметрична и находится под действием симметричной нагрузки, очевидно, вертикальные реакции и должны быть равными. Найдем их из уравнения проекций всех действующих на систему сил на вертикальную ось: . Следовательно, .
Теперь приступим к определению усилий в стержнях фермы. Прежде всего выделим нулевые стержни. Из рассмотрения узла 5 на основании признака 2 нулевых стержней следует, что стержень 5-6 нулевой.
Мысленно рассечем ферму сечением, изображенным на рис.32 и рассмотрим равновесие левой части. Напомним, что положительное значение продольного усилия соответствует растяжению стержня, а отрицательное — сжатию. Поэтому при составлении уравнений равновесия будем считать неизвестные стержневые усилия растягивающими.
Напомним, что положительное значение продольного усилия соответствует растяжению стержня, а отрицательное — сжатию. Поэтому при составлении уравнений равновесия будем считать неизвестные стержневые усилия растягивающими.
Из уравнения моментов относительно точки А находим , а из уравнения моментов относительно точки В (ее положение легко определяется из подобия треугольников А43 и АВС) находим N3-6=60КН.
Усилие N4-6 можно определить из уравнения проекций всех сил на вертикальную ось . Угол можно определить, например, из треугольника АВС: . Следовательно, .
Усилия в остальных стержнях левой половины фермы можно найти, например вырезанием узлов 2, 3 и 4.
Рассотрим равновесие узла 2 (рис.33). Он соединяет три стержня, но в одном из них усилие уже найдено — усилие в стержне 2-5 является сжимающим и равно 40КН. Следовательно, двух уравнений равновесия этого узла будет достаточно, чтобы определить усилия в двух других стержнях. Из треугольника 123 следует, что . Составим уравнения проекций сил на горизонтальную и вертикальную оси: и . Сопоставляя эти два уравнения, учитывая, что , получим: и .
Составим уравнения проекций сил на горизонтальную и вертикальную оси: и . Сопоставляя эти два уравнения, учитывая, что , получим: и .
Рассмотрим равновесие узла 4 (рис.34). Он также соединяет три стержня, но в одном из них усилие уже найдено — усилие в стержне 4-6 является сжимающим и равно 22,361КН. Следовательно, двух уравнений равновесия этого узла будет достаточно, чтобы определить усилия в двух других стержнях. Из уравнения проекций сил на горизонтальную ось следует: . Из уравнения проекций сил на вертикальную ось следует:
Теперь рассмотрим равновесие узла 3 (рис.35). Усилия в трех стержнях из четырех, соединяющихся в этом узле, уже известны. Из уравнения проекций всех сил на горизонтальную ось находим . Запишем уравнение проекций сил на вертикальную ось: . Полученное равенство является истинным, что подтверждает правильность полученных значений усилий в стержнях ферм.
Итак, значения усилий в стержнях левой половины фермы определены. Усилия в стержнях на правой половине фермы находятся исходя из симметрии фермы и симметричности приложенной к ней нагрузки. Значения усилий (КН), определенные в результате расчета, приводятся на рис.36.
Значения усилий (КН), определенные в результате расчета, приводятся на рис.36.
Проверки правильности определения усилий в стержнях фермы также можно осуществить вырезанием узлов или использованием способа сечений.
Сопоставление балочных ферм различных типов.
Перед проектировщиком может встать задача выбора фермы наиболее рациональной конструкции. Под наиболее рациональной понимается такая конструкция, при которой усилия в стержнях фермы оказываются минимальными, что позволяет уменьшить расход материала, а значит и ее собственный вес. Кроме того, необходимо принимать во внимание вопросы, связанные с технологией изготовления, транспортировки и монтажа конструкций ферм.
Рассмотрим четыре фермы, перекрывающие один и тот же пролет -30м, имеющие одинаковую высоту в середине пролета — 5м, характеризующиеся одним и тем же числом панелей- 6 и находящиеся под действием одной и той же нагрузки — ко всем узлам верхнего пояса приложены напрвленные вертикально вниз силы величиной 10КН, а ко всем узлам нижнего пояса — 30КН.
Первая ферма — с параллельными поясами и нисходящими раскосами (рис.37), вторая — с параллельными поясами и треугольной решеткой с дополнительными вертикальными стойками (рис.38), третья — с параболическим очертанием верхнего пояса и нисходящими раскосами (рис.39), четвертая — треугольная стропильная ферма с нисходящими раскосами (рис.40). На рисунках приводятся значения усилий (КН) в стержнях ферм, полученные в результате их статического расчета[2].
Как и следовало ожидать, стержни верхнего пояса во всех четырех случаях оказались сжатыми, а нижнего — растянутыми.
В балочных фермах с параллельными поясами в стержнях верхнего и нижнего поясов усилия увеличиваются от опор к центру пролета. Поэтому, если стержни верхнего и нижнего поясов выполняются постоянного по длине пролета сечения, то материал стержней поясов вблизи опор используется нерационально. Изготовление же стержней поясов фермы переменного по длине фермы сечения обычно является нерациональным из технологических соображений. Поэтому фермы с параллельными поясами не используют при очень больших пролетах и нагрузках, когда задача экономии материала и облегчения конструкции фермы приобретает особую важность.
Поэтому фермы с параллельными поясами не используют при очень больших пролетах и нагрузках, когда задача экономии материала и облегчения конструкции фермы приобретает особую важность.
Нисходящие раскосы в фермах с параллельными поясами работают на растяжение, восходящие — на сжатие, причем замена раскоса с нисходящего на восходящий приводит к изменинению знака усилия в нем, но абсолютная величина усилия остается постоянной.
Балочные фермы с параболическим очертанием верхнего пояса лишены основного недостатка ферм с параллельными поясами. Усилия в стержнях нижнего пояса постоянны по длине пролета, а верхнего пояса — меняются незначительно. Раскосы в такой ферме вообще практически не работают. То есть ферма этого типа представляется наиболее выгодной с точки зрения напряженного состояния. В то же время технология такой фермы несколько сложнее. Поэтому фермы с параболическим или близким к нему, трапецеидальным очертанием верхнего пояса используют для перекрытия весьма больших пролетов и при действии достаточно высокой нагрузки.
В треугольной ферме величины усилий в стержнях заметно выше, чем в фермах других типов. Усилия в верхнем и нижнем поясах распределены крайне неравномерно по длине пролета, увеличиваясь от середины пролета к опорам. Таким образом, треугольные фермы являются наименее выгодными по сравнению с фермами других типов. Их имеет смысл использовать там, где применение ферм других типов нерационально по конструктивным соображениям, например, в качестве стропильных ферм в двускатных зданиях небольшой ширины.
Расчет ферм на подвижную нагрузку.
Подвижной нагрузкой будем называть такую, как правило, вертикальную нагрузку, которая может перемещаться в пределах сооружения. Подобная нагрузка создается, например, движущимся по мосту транспортом или перемещающимися по подкрановым путям мостовыми кранами. При этом усилия, возникающие в сооружении, будут зависеть от положения нагрузки. Будем считать, что нагрузка перемещается по сооружению с небольшими ускорениями, поэтому динамическими эффектами, возникающими при этом можно пренебречь.
Задача расчета сооружений на подвижную нагрузку состоит в определении внутренних усилий в ее сечениях при любом ее положении. В частности, важно найти невыгоднейшее или опасное положение нагрузки, т.е. такое положение, при котором усилие в данном элементе конструкции достигает максимального по модулю значения. По усилиям, возникающим при невыгоднейшем положении груза, и выполняется подбор сечения стержней в системе.
Поскольку фермы часто используются в пролетных строениях мостов, в качестве несущих конструкций эскалаторов в метрополитенах, как стрелы подъемных кранов, их часто приходится расcчитывать на действие подвижной нагрузки.
Расчет стержневых систем на подвижную нагрузку выполняется при помощи линий влияния. Линия влияния внутреннего усилия в каком -либо сечении стержня — график зависимости этого усилия от положения единичной вертикальной силы на ездовой линии.
Рассмотрим вначале простую балку на двух опорах, перекрывающую пролет L (рис. 41). Построим линии влияния реакции в левой опоре и изгибающего момента в сечении в центре балки.
41). Построим линии влияния реакции в левой опоре и изгибающего момента в сечении в центре балки.
Пусть единичная сила приложена на расстоянии х от левой опоры. Из условия равенства нулю суммы проекций всех действующих на систему сил на вертикальную ось имеем . Из условия равенства нулю суммы всех приложенных к системе моментов относительно точки А имеем . Отсюда следует, что . График данной зависимости и представляет собой линию влияния опорной реакции (рис.41). При построении линий влияния ее положительные ординаты принято откладывать вверх.
Итак, при перемещении груза от левой опоры к правой величина опорной реакции уменьшается от единицы до нуля по линейному закону.
Для построения линии влияния изгибающего момента необходимо рассмотреть два случая, когда груз находится левее и правее рассматриваемого сечения С. В первом случае () выражение для изгибающего момента имеет вид . Во втором случае . Соответственно, линия влияния состоит из двух ветвей (рис.41). Изгибающий момент в центре пролета балки равен нулю при нахождении груза на опорах и достигает максимального значения, когда положение единичной силы совпадает с рассматриваемым сечением (при ).
Важно четко уяснить разницу между эпюрой и линией влияния. При построении эпюры определяются внутренние усилия в различных сечениях системы при неподвижной нагрузке, а при построении линии влияния определяется усилие в каком-то одном сечении при разных положениях единичной силы, действующей на систему.
В фермах нагрузка обычно передается на узлы посредством вспомогательных конструкций, например через настил и систему продольных и поперечных балок (рис.42). То есть, если единичная сила находится на ездовой линии и не над узлом фермы, то все равно имеет место узловая передача нагрузки, а значит в стержнях фермы не возникает никаких усилий, кроме продольных.
Для построения линий влияния в стержнях ферм применяют те же приемы, что и при определении усилий в них от действия неподвижной нагрузки, в частности способ сечений. Необходимо только задаться координатой единичной силы на ездовой линии и проанализировать зависимость величины усилия в стержне от ее изменения.
В некоторых фермах со сложной решеткой, например шпренгельных, линии влияния могут иметь довольно сложный вид.
В раскосных фермах и фермах с треугольной решеткой ситуация несколько проще. Усилие в стержне при нахождении единичной силы слева от панели (рис.43), в которой находится этот стержень, будет меняться по одному закону, при нахождении справа от нее (рис.44) — по другому закону, а при нахождении в пределах данной панели (рис.45) — по третьему закону. В последнем случае необходимо учитывать, что часть от единичного усилия через вспомогательные конструкции передается на узел, лежащий на ездовой линии, слева от рассматриваемой панели, т.е. на часть фермы слева от сечения, а оставшаяся часть — на узел справа от рассматриваемой панели, т.е. с другой стороны от сечения. Таким образом, линии влияния продольного усилия в стержнях таких ферм в общем случае имеют три участка (рис.46), причем часть линии влияния в пределах панели, которой принадлежит данный стержень, носит название передаточной прямой.
После того, как для стержня построена линия влияния, с ее помощью можно решить следующие задачи.
1. Пусть на ездовой линии находится груз величиной Р. Тогда усилие в стержне составит , где y — ордината линии влияния под точкой приложения силы Р. Действительно, y -усилие, возникающее в стержне от действия приложенной в данной точке единичной силы. В силу линейности задачи, при увеличении нагрузки в Р раз, усилие в стержне тоже возрастет во столько-же раз.
На основании принципа независимости действия сил, если на ездовой линии имеется система из n сил, то усилие в стержне будет определяться по формуле:
где — ордината линии влияния под i-ой силой величиной Pi (рис.47). Таким образом, линии влияния могут быть использованы и для определения усилий в стержнях ферм и при действии неподвижной нагрузки. Это может быть удобно, если нужно выполнить большое число расчетов для различных комбинаций нагрузок, приложенных к ферме.
2. Пусть на участке длиной ездовой линии действует равномерно распределенная нагрузка интенсивностью q. Во избежание недоразумений подчеркнем, что здесь как и ранее, так и далее, считается, что нагрузка приложена к вспомогательным конструкциям, а с них — передается на узлы фермы. В этом случае усилие в стержне фермы определяется по формуле:
В этом случае усилие в стержне фермы определяется по формуле:
где — площадь, ограниченная линией влияния под зоной действия нагрузки q (рис.48). Действительно, выделим в зоне действия нагрузки q участок бесконечно малой длиной dx (рис.48). Элементарная равнодействующая сила, действующая на ферму, с этого участка составляет , а усилие, возникающее от ее действия в стержне, в соответствии с формулой (3) составит .Для того, чтобы найти усилие в стержне от действия всей нагрузки, необходимо проинтегрировать dN по длине :.
Очевидно, площадь в (4) необходимо определять с учетом знака. То есть, часть площади w снизу от горизонтальной оси учитывается со знаком “минус”.
3. Пусть система грузов перемещается по ездовой линии, причем расстояния между грузами остаются постоянными. Такая ситуация имеет место, например, при движении поезда или мостового крана по пролетному строению моста или по подкрановым путям. Невыгоднейшее положение данной системы грузов возможно только при условии, что один из грузов находится над какой-либо вершиной линии влияния (рис. 49). Подчеркнем, что это условие необходимое, но недостаточное. Иными словами, не при любом подобном положении нагрузки усилие в стержне имеет экстремальное значение.
49). Подчеркнем, что это условие необходимое, но недостаточное. Иными словами, не при любом подобном положении нагрузки усилие в стержне имеет экстремальное значение.
Например, для случая, приведенного на рис.49, усилие от системы грузов в соответствии с (3) составляет . При сдвиге системы грузов вправо на величину такую, что ни одна из сил, приложенных к системе, не перейдет при этом через какую-либо вершину линии влияния и не выйдет за пределы фермы, усилие в стержне АВ составит:
.
При сдвиге влево на ту же величину оно составит .
Здесь и — абсолютные значения изменения ординаты линии влияния под i-м грузом при сдвиге системы грузов вправо и влево соответственно, — абсолютное значение угла наклона линии влияния на i-м ее участке (рис.49).
Таким образом, изменение величины усилия в стержне при сдвиге груза вправо составит , а при сдвиге влево . Очевидно, эти значения могут быть как одного так и разных знаков. Если и оказываются одного знака, то это значит, что при сдвиге системы грузов как вправо так и влево усилие в стержне либо уменьшается, либо увеличивается, то есть оно имеет локальный экстремум.
В то же время, для случая когда ни один из грузов не находится над вершиной линии влияния, величины и могут быть только разных знаков, а значит эктремум усилия в стержне в этом случае невозможен.
Действительно, рассмотрим в качестве примера ситуацию, изображенную на рис.50. В этом случае при сдвиге вправо:
, .
А при сдвиге влево:
, .
Сопоставляя выражения для и , можно сделать вывод, что они не могут быть одного знака.
Итак, для поиска максимально и минимально возможных усилий в стежнях фермы при действии на нее подвижной системы грузов достаточно рассматривать только такие положения этой системы, при которых хотя бы один из грузов находится над какой-либо вершиной линии влияния.
Пример расчета фермы на подвижную нагрузку.
Рассмотрим ферму, изображенную на рис.31. Необходимо:
1. Используя теорию линий влияния, определить усилие в стержне фермы 2-3 от действия неподвижной системы сил, изображенной на рис.31.
2. Определить максимальное и минимальное усилия в стержне фермы 2-3 при движении по ездовой линии (по горизонтали от узла 1 к узлу 10) системы из двух сил (рис.51).
Определить максимальное и минимальное усилия в стержне фермы 2-3 при движении по ездовой линии (по горизонтали от узла 1 к узлу 10) системы из двух сил (рис.51).
3. Определить усилие от постоянной равномерно распределенной нагрузки q=10КН/м, приложенной к поясу фермы, совпадающему с ездовой линией (рис.52).
Построим линию влияния для стержня фермы 2-3[3]. Для этого достаточно определить усилие в этом стержне при различных положениях единичной силы на ездовой линии.
Если единичная сила находится на расстоянии х от левой опоры, то реакция в последней будет составлять , а в правой опоре — (рис.53).
Cоставим уравнения равновесия узла 2 (рис.54):
, , откуда следует, что . Поскольку , нагрузки к узлу 2 не приложены, т.к. он не лежит на ездовой линии, это уравнение справедливо при любом положении грузов на ней. Для определения воспользуемся способом сечений, причем рассмотрим два случая, когда единичный груз находится слева от панели, в которой располагается стержень 2-5 (рис. 55), и справа от нее (рис.56).
55), и справа от нее (рис.56).
Для первого случая (рис.55) уравнения равновесия моментов относительно точки А примет вид:
, откуда: . Следовательно, при нахождении единичного груза слева от рассеченной панели (x<2м) , а .
Согласно этой формуле, при x=0 ордината линии влияния, как и следовало ожидать, равна нулю, а при x=2м она равна 1/2. По этим точкам строится левая ветвь линии влияния (до точки С на рис.57)
Для второго случая (рис.56) из аналогичных рассуждений получим: , откуда: . Следовательно, при нахождении единичного груза справа от рассеченной панели (x>4м) , а . Таким образом, при x=4м ордината линии влияния равна 1 (точка D на рис.57), а на правой опоре, как и следовало ожидать -нулю. По этим точкам строится правая ветвь линии влияния, и далее передаточная прямая CD. В рассматриваемом случае ее направление, как мы видим, совпадает с направлением левой ветви линии влияния, а сама линия влияния оказалась симметричной.
Теперь приступим к определению усилий в стержне 2-3.
Для заданной неподвижной узловой нагрузки (рис.31) в соответствии с формулой (3) найдем величину усилия в стержне: . Этот же ответ был получен нами ранее в разделе “Пример расчета фермы на неподвижную нагрузку” без использования линий влияния, что подтверждает правильность проделанных вычислений.
Наиневыгоднейшим положением подвижной системы двух сил на ездовой линии (рис.51) будет положение, когда одна из них находится ровно посередине пролета фермы (рис.58), т.к. в этом случае одна из сил оказывается над единственной в рассматриваемом случае вершиной линии влияния. Ордината линии влияния под силой в центре фермы равна 1, ординату под точкой приложения второй силы легко определить из подобия треугольников: , откуда y=0,8 (рис.58). В соответствии с (3) усилие в стержне составит . В силу симметрии линии влияния, в случае, когда над ее вершиной в центре пролета фермы окажется не левая, а правая сила, результат будет тем же.
Построенная линия влияния не имеет отрицательных ординат, следовательно, при любом положении системы сил на ездовой линии в стержне будут возникать только растягивающие усилия. Поэтому, максимальным возможным усилием в стержне 2-3 для рассматриваемой подвижной нагрузки является 36КН, минимальным -0 КН.
Поэтому, максимальным возможным усилием в стержне 2-3 для рассматриваемой подвижной нагрузки является 36КН, минимальным -0 КН.
Наконец, определим усилие в стержне от действия неподвижной равномерно распределенной по всей длине ездовой линии нагрузки (рис.52) q=10 КН/м. Площадь фигуры, ограниченной линией влияния (рис.57) составляет . Размерность площади фигуры оказалась такой, поскольку единичная сила, а следовательно и ординаты линии влияния продольного усилия не имеют размерности.
Теперь, в соответствии с формулой (4), определим усилие в стержне: .
Глоссарий
Висячие системы
Ездовая линия
Жесткий диск
Комбинированные системы
Линия влияния
Невыгоднейшее положение нагрузки
Нулевой стержень
Опасное положение нагрузки
Панель фермы
Передаточная прямая
Подвижная нагрузка
Пояс фермы верхний
Пояс фермы нижний
Проезжий пояс
Раскос
Раскос восходящий
Раскос нисходящий
Решетка фермы
Статический метод анализа геометрической неизменяемости ферм
Стойка
Структурный анализ фермы
Узлы фермы
Ферма
Ферма арочная
Ферма балочная
Ферма консольная
Ферма консольно-балочная
Ферма простейшая
Ферма раскосная
Ферма с треугольной решеткой
Лекция «Моделирование поведения потребителей» также может быть Вам полезна.
Ферма шпренгельная
Шарнирная схема
Шпренгель
[1] В.Г.Шухов (1853-1939) — выдающийся русский инженер, автор конструкций легких и экономичных перекрытий различных типов, высотной мачты первой радиотелеграфной станции в Москве (1921), известной как башня Шухова, автор многочисленных конструкторских решений в области добычи, переаботки, хранения и транспортировки нефти.
[2] Данные и результаты расчетов взяты из книги: Шишман Б.А. Статика сооружений: Учебник для техникумов.-М.:Стройиздат, 1989.-384с.”
[3] В состав настоящего учебника входит программа для ЭВМ “Построение линий влияния в фермах”, разаработанная кафедрой строительной механики и теории упругости СПбГТУ.
Антипин М.И. Расчет плоских статически определимых ферм
- формат doc
- размер 340.5 КБ
- добавлен 04 марта 2010 г.
Методическое пособие по расчету плоских ферм. Уделяется внимание
конструкции ферм, расчету ферм – определению внутренних усилий в
стержнях различными способами. Приводятся примеры расчета плоской
фермы.
Уделяется внимание
конструкции ферм, расчету ферм – определению внутренних усилий в
стержнях различными способами. Приводятся примеры расчета плоской
фермы.
Читать онлайн
Похожие разделы
- Академическая и специальная литература
- Металлургия
- Металловедение
- Механические и физические свойства металлов
- Дефекты металлов
- Усталость металлов
Смотрите также
- формат doc
- размер 3.63 МБ
- добавлен
05 декабря 2009 г.

Содержание: общие указания по выполнению расчетно-проектировочных работ. Используемые обозначения. Растяжение-сжатие. Расчет статически определимых стержневых систем. Примеры решения задач. Подбор сечения стержня, подверженного растяжению-сжатию (задача № 1). Определение напряжений и перемещений в стержне при растяжении-сжатии с учетом собственного веса (задача № 2). Определение грузоподъемности статически определимой конструкции, работающей на р…
- формат doc
- размер 3.61 МБ
- добавлен 05 декабря 2009 г.
Содержание: Общие указания по выполнению расчетно-проектировочных работ. Используемые обозначения. Изгиб. Расчет статически определимых балок. Примеры решения задач. Определение внутренних усилий в балках (задачи № 12–15). Пример 1. Пример 2. Проверка прочности балок при плоском поперечном изгибе (задачи № 16–19). Пример 1. Пример Пример 3. Определение перемещений и проверка жесткости балок (задачи № 19, 20). Примеры решения задач Определение пер…
Пример 1. Пример Пример 3. Определение перемещений и проверка жесткости балок (задачи № 19, 20). Примеры решения задач Определение пер…
- формат doc
- размер 1.65 МБ
- добавлен 04 апреля 2009 г.
Северодонецк, ТИ СНУ им. В. Даля. Расчет статически неопределимых стержней при растяжении. Расчет круглого вала на прочность и жесткость при кручении. Полный расчет балок на прочность. Расчет плоских рам. Статически неопределимые рамы. Сложный изгиб. Расчет на устойчивость сжатого стержня. Расчет на прочность при ударных нагрузках. Заархивированная папка с файлами .DOC.
Практикум
- формат pdf
- размер 730.86 КБ
- добавлен
25 ноября 2011 г.

Методические указания. Краснодар: Изд. КубГТУ, 2008. — 43 с. Содержание: Задача Геометрические характеристики плоских сечений Задача Расчет ступенчатого стержня на осевое растяжение Задача Расчет статически неопределимой стержневой системы Задача Кручение вала круглого поперечного сечения Задача Плоское напряженное состояние в точке тела Задача Расчеты на прочность при плоском изгибе Задача Расчет статически неопределимой балки Задача Косой изг…
- формат doc
- размер 1004.73 КБ
- добавлен 15 апреля 2010 г.
Расчет стержневых статически неопределимых систем при растяжении (сжатии). Расчет валов и пружин на жесткость и прочность при кручении. Построение эпюр внутренних силовых факторов для балок и рам. Задачи на прочность и жесткость при изгибе статически определимых систем. Расчет статически неопределимых систем по методу сил. Расчеты на прочность при сложном напряженном состоянии. Задачи на прочность при циклических напряжениях. Расчеты элементов ко…
Расчет статически неопределимых систем по методу сил. Расчеты на прочность при сложном напряженном состоянии. Задачи на прочность при циклических напряжениях. Расчеты элементов ко…
program
- формат exe
- размер 336.35 КБ
- добавлен 12 февраля 2008 г.
Программа для решения задач по сопромату. Расчет плоских балок и рам методом конечных элементов. Расчет статически неопределимых балок и рам. Построение эпюр изгибающих моментов, перерезываюших и продольных сил. Расчет перемещений и реакций опор.rn
program
- формат exe
- размер 372.59 КБ
- добавлен
12 января 2009 г.

Полюс — программа для расчета стержневых конструкций. Полюс умеет выполнять расчет статически определимых и неопределимых конструкций на статическое силовое, кинематическое и температурное воздействие. Расчет ведется с помощью одного из вариантов метода перемещений, который разработал профессор Петрозаводского Государственного Университета Ю.Б.Гольдштейн. Изюминка программы — простой, интуитивно-понятный интерфейс, позволяющий задать и получить р…
software
- формат txt, doc, exe, gif, htm
- размер 319.93 КБ
- добавлен 03 октября 2010 г.
В архиве программа, методическое указание к применению и два примера. Программа может быть полезна при расчете плоских ферм при выполнении курсовых проектов и расчетно-графических работ студентами очной и заочной форм обучения.
software
- формат exe, txt
- размер 4.06 МБ
- добавлен 03 января 2012 г.
Программа с графическим интерфейсом для расчета статически определимых балок, которая сама сделает за вас сложные расчеты, построит за вас эпюры поперечних сил и изгибательных моментов, и даже подготовит отчет о этих расчетах, который вы сможете распечатать.rn
- формат pdf
- размер 815.93 КБ
- добавлен 06 февраля 2009 г.
В сборнике представлены примеры решения задач для студентов большинства Российских вузов по темам: — Растяжение и сжатие: статически определимые системы статически неопределимые системы; — Кручение круглого бруса; — Изгиб плоских балок; — Геометрические характеристики плоских сечений; — Устойчивость сжатых стержней.
УРОК по дисциплине «Техническая механика» на тему «Расчет статически определимых ферм» с презентациями. | Электронный образовательный ресурс:
Слайд 1
РАСЧЁТ ФЕРМ Фермой называется геометрически неизменяемая конструкция, состоящая из стержней. Места соединений стержней называются узлами
Слайд 12
Если оси всех стержней и вся приложенная к ферме нагрузка расположены в одной плоскости, ферма называется плоской. В дальнейшем будем рассматривать только плоские фермы. РАСЧЁТ ФЕРМ
Слайд 13
РАСЧЁТ ФЕРМ Примером плоской фермы может служить стропильная ферма
Слайд 15
РАСЧЁТ ФЕРМ Другим примером плоской фермы могут служить конструкции железнодорожного моста
Слайд 16
При проектировании и эксплуатации фермы соблю-даются следующие условия: 1. все стержни прямолинейны; 2. вес стержней пренебрежимо мал по сравнению с эксплуатационной нагрузкой; 3. нагрузка прикладывается только к узлам фермы. РАСЧЁТ ФЕРМ
Слайд 17
РАСЧЁТ ФЕРМ Как видно, нагрузка на ферму передаётся через продольные прогоны, которые прикреплены к узлам фермы.
Слайд 18
РАСЧЁТ ФЕРМ Эксплуатационная нагрузка через поперечные балки передаётся на узлы боковых ферм моста.
Слайд 19
РАСЧЁТ ФЕРМ Эксплуатационная нагрузка через поперечные балки передаётся на узлы боковых ферм моста.
Слайд 20
При соблюдении указанных условий усилиями, возни-кающими при изгибе стержней, можно пренебречь по сравнению с усилиями, возникающими при растяжении – сжатии. Это упрощающее предположение положено в основу методов расчёта ферм. РАСЧЁТ ФЕРМ
Слайд 21
РАСЧЁТ ФЕРМ В реальной ферме крепления стержней в узлах жёсткие. В расчётной схеме крепления стержней считают шарнирными, что связано с реализацией принятого упрощающего предположения о возможности пренебречь усилиями, возникающими при изгибе.
Слайд 22
РАСЧЁТ ФЕРМ При соблюдении оговорённых упрощающих условий каждый стержень фермы оказывается нагруженным силами, приложенными на концах стержня.
Слайд 23
РАСЧЁТ ФЕРМ При соблюдении оговорённых упрощающих условий каждый стержень фермы оказывается нагруженным силами, приложенными на концах стержня. Силы, приложенные в одной точке можно заменить равнодействующей.
Силы, приложенные в одной точке можно заменить равнодействующей.
Слайд 24
или РАСЧЁТ ФЕРМ При соблюдении оговорённых упрощающих условий каждый стержень фермы оказывается нагруженным силами, приложенными на концах стержня. Силы, приложенные в одной точке можно заменить равнодействующей. Усилие в стержне считается положительным, если он растянут и отрицательным, если стержень сжат В результате расчёта фермы необходимо определить реак-ции опор и найти усилия во всех стержнях фермы. Методы расчёта ферм рас-смотрим на примере.
Слайд 25
? Метод вырезания узлов в некоторых случаях представ- ляется неоправданно трудоёмким. Рассмотрим ферму. Требуется определить усилие только в одном, выде-ленном на чертеже, стержне. РАСЧЁТ ФЕРМ
Слайд 26
Для определения искомой неизвестной необходимо со-ставить и решить систему, состоящую из 21-го уравне-ния. Три уравнения равновесия фермы в целом потребу-ются для определения опорных реакций. Ещё 18 уравнений появятся, по мере рассмотрения рав- новесия узлов при движении по кратчайшему пути от ле- вого (неподвижного) шарнира к нужному нам стержню. Понятно, что при решении системы, состоящей из 21-го уравнения, можно допустить ошибку. РАСЧЁТ ФЕРМ
Понятно, что при решении системы, состоящей из 21-го уравнения, можно допустить ошибку. РАСЧЁТ ФЕРМ
Слайд 27
Чтобы убедиться в правильности полученного результа-та, необходимо составить проверочные уравнения. Для этого придётся продолжить рассмотрение равновесия уз-лов фермы. В четырёх уравнениях, составленных для последних двух узлов, будет только одна неизвестная величина – усилие в последнем стержне. Оставшиеся три уравнения должны выполняться тождественно, то есть выполняют роль проверочных уравнений. РАСЧЁТ ФЕРМ
Слайд 28
Понятно, что результат проверки может быть разным. Возможны варианты. Первый вариант Второй вариант РАСЧЁТ ФЕРМ
Слайд 29
ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ФЕРМЫ МЕТОДОМ СКВОЗНЫХ СЕЧЕНИЙ Метод сквозных сечений состоит в том, что ферма раз- деляется сечением на две части и рассматривается рав- новесие одной из этих частей. Сечение проводится через стержень, в котором необходимо определить усилие. РАСЧЁТ ФЕРМ
Слайд 30
Метод сквозных сечений состоит в том, что ферма раз- деляется сечением на две части и рассматривается рав- новесие одной из этих частей. Сечение проводится через стержень, в котором необходимо определить усилие. РАСЧЁТ ФЕРМ
Сечение проводится через стержень, в котором необходимо определить усилие. РАСЧЁТ ФЕРМ
Слайд 31
Можно рассмотреть равновесие любой из образовав-шихся частей фермы. Для рассматриваемой части «разрезанные» стержни служат опорами. Их реакции входят в систему внешних сил, приложенных к рассма-триваемой части фермы. РАСЧЁТ ФЕРМ
Слайд 32
РАСЧЁТ ФЕРМ Можно рассмотреть равновесие любой из образовав-шихся частей фермы. Для рассматриваемой части «разрезанные» стержни служат опорами. Их реакции входят в систему внешних сил, приложенных к рассма-триваемой части фермы.
Слайд 33
РАСЧЁТ ФЕРМ Любая из частей фермы находится под действием плоской системы сил, для которой можно составить только три независимых уравнения равновесия. По этой причине сечение, по возможности, проводится через три стержня фермы. Рассмотрим пример расчёта фермы при помощи мето-да сквозных сечений.
Слайд 34
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Слайд 35
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Слайд 36
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Слайд 37
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Слайд 38
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Слайд 39
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Слайд 40
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Слайд 41
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Слайд 42
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. Если N
Слайд 43
Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. РАСЧЁТ ФЕРМ Если N > 2n – 3, конструкция будет жёсткой, но число неизвестных будет больше числа уравнений равновесия, в которые эти неизвестные входят. N = 6 > 2n – 3 = 5. Конструкция будет жёст-кой, но наличие «лишнего» стержня, конеч-но, будет иметь некоторые последствия.
Простейшая жёсткая конструкция имеет три узла и три стержня. Для присоединения каждого из оставшихся n – 3 узлов необходимы два стержня. Таким образом, получаем: УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ N = 3 + 2 (n – 3) = 2 n – 3. РАСЧЁТ ФЕРМ Если N > 2n – 3, конструкция будет жёсткой, но число неизвестных будет больше числа уравнений равновесия, в которые эти неизвестные входят. N = 6 > 2n – 3 = 5. Конструкция будет жёст-кой, но наличие «лишнего» стержня, конеч-но, будет иметь некоторые последствия.
Слайд 44
УСЛОВИЕ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ФЕРМЫ Ферма называется статически определимой, если чис- ло неизвестных равно числу уравнений равновесия, в ко- торые эти неизвестные входят. Для фермы, имеющей n узлов, можно составить 2n независимых уравнений рав- новесия. В число неизвестных входят N усилий в стерж- нях фермы и три составляющие реакций внешних опор. Таким образом, ферма будет статически определимой при выолнении условия N = 2n – 3, которое, как видно, совпадает с условием жёсткости. РАСЧЁТ ФЕРМ
РАСЧЁТ ФЕРМ
Слайд 45
«Лишние» опоры – ненужные для обеспечения равновесия абсолютно твёрдого тела – могут появиться по двум основным причинам. Во-первых, причины могут быть технологическими: перекрытие кладётся на две стены, хотя теоретически можно было бы обойтись одной заделкой. Во-вторых, дополнительные опоры приходится устанавливать, чтобы предотвратить недопустимо большие деформации, опасные для прочности конструкции. РАСЧЁТ ФЕРМ УСЛОВИЕ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ФЕРМЫ
3 метода анализа ферм | Engineersdaily
Перед обсуждением различных методов анализа ферм уместно сделать краткое введение.
Конструкция, состоящая из нескольких стержней, соединенных штифтами на концах и образующих устойчивый каркас, называется фермой. Обычно предполагается, что нагрузки и реакции действуют на ферму только в узлах. Ферма обычно состоит из треугольных элементов со стержнями на верхнем поясе при сжатии и на нижнем поясе при растяжении. Фермы широко используются для мостов, длинных пролетных крыш, электрических мачт и космических конструкций.
Фермы статически определимы, когда все усилия на стержнях могут быть определены только из уравнений статики. В противном случае ферма статически неопределима. Ферма может быть статически (внешне) определимой или неопределенной по реакциям (более 3 или 6 реакций в 2D или 3D задачах соответственно).
| Правила знаков |
Для анализа ферм предполагается, что:
- Стержни соединены штифтами.
- Соединения представляют собой шарниры без трения.
- Нагрузки действуют только на соединения.
- Напряжение в каждом стержне постоянно по его длине.
Целью анализа фермы является определение реакций и усилий на стержнях. Методы, используемые для проведения анализа с помощью уравнений равновесия и путем рассмотрения только частей конструкции путем анализа ее диаграммы свободного тела для решения неизвестных.
Начнем с предположения, что все элементы испытывают реакцию растяжения. Натяжной элемент испытывает тяговые усилия на обоих концах стержня и обычно обозначается положительным знаком (+ve). Когда на элемент действует толкающее усилие с обоих концов, говорят, что стержень находится в режиме сжатия и обозначается знаком минус (-ve).
В методе суставов вокруг сустава делается виртуальный разрез, а часть разреза изолируется в виде диаграммы свободного тела (FBD). Используя уравнения равновесия ∑ Fx = 0 и ∑ Fy = 0, можно решить неизвестные силы-члены. Предполагается, что все элементы соединены вместе в виде идеального штифта и что все силы находятся в напряжении (положительные реакции).
Воображаемое сечение может полностью проходить вокруг соединения в ферме. Сустав стал свободным телом, находящимся в равновесии под действием приложенных к нему сил. Уравнения ∑ H = 0 и ∑ V = 0 могут быть применены к соединению для определения неизвестных сил в элементах, встречающихся в нем. Очевидно, что на стыке этих двух уравнений можно определить не более двух неизвестных.
Очевидно, что на стыке этих двух уравнений можно определить не более двух неизвестных.
Простая модель фермы, опирающаяся на шарнирную и роликовую опору на конце. Каждый треугольник имеет одинаковую длину L и является равносторонним, где градус угла θ равен 60 ° на каждом угле. Опорные реакции Ra и Rc можно определить, взяв точку момента либо в точке A, либо в точке C, тогда как Ha = 0 (другая горизонтальная сила отсутствует).
Вот несколько простых рекомендаций по этому методу:
- Сначала нарисуйте диаграмму свободного тела (FBD),
- Решите реакции данной структуры,
- Выберите соединение с минимальным количеством неизвестных (не более 2) и проанализируйте его с ∑ Fx = 0 и ∑ Fy = 0,
- Перейдите к остальным суставам и снова сосредоточьтесь на суставах, которые имеют минимальное количество неизвестных,
- Проверить усилия на стержнях в неиспользуемых соединениях с ∑ Fx = 0 и ∑ Fy = 0,
- Занесите в таблицу усилия на стержень независимо от того, находится ли он в реакции растяжения (+ve) или сжатия (-ve).

На рисунке показаны 3 выбранных соединения в точках B, C и E. Силы в каждом элементе можно определить по любому соединению или точке. Лучше всего начать с выбора самого простого соединения, такого как соединение C, где реакция Rc уже получена и только с двумя неизвестными силами FCB и FCD. Оба могут быть оценены с помощью правил ∑ Fx = 0 и ∑ Fy = 0. В соединении E действуют 3 неизвестные силы FEA, FEB и FED, что может привести к более сложному решению по сравнению с 2 неизвестными значениями. В целях проверки соединение B выбирается так, чтобы показать, что уравнение ∑ Fx равно ∑ Fy, что приводит к нулевому значению, ∑ Fx = ∑ Fy = 0. Состояние каждого стержня должно быть четко указано, например, находится ли он в напряжении (+ ve) или в сжатом (-ve) состоянии.
Тригонометрические функции:
Определение угла между стержнями x и z…
- Cos θ = x / z
- Sin θ = y / z
- Тан θ = у / х
Метод сечения является эффективным методом, когда необходимо определить силы во всех элементах фермы. Если требуется только несколько сил, действующих на ферму, то самый быстрый способ найти эти силы — метод сечений. В этом методе воображаемая линия разреза, называемая сечением, проводится через устойчивую и определенную ферму. Таким образом, сечение делит ферму на две отдельные части. Поскольку вся ферма находится в равновесии, любая ее часть также должна находиться в равновесии. Можно рассмотреть любую из двух частей фермы и применить три уравнения равновесия ∑ Fx = 0, ∑ Fy = 0 и ∑ M = 0 для расчета сил на стержнях.
Если требуется только несколько сил, действующих на ферму, то самый быстрый способ найти эти силы — метод сечений. В этом методе воображаемая линия разреза, называемая сечением, проводится через устойчивую и определенную ферму. Таким образом, сечение делит ферму на две отдельные части. Поскольку вся ферма находится в равновесии, любая ее часть также должна находиться в равновесии. Можно рассмотреть любую из двух частей фермы и применить три уравнения равновесия ∑ Fx = 0, ∑ Fy = 0 и ∑ M = 0 для расчета сил на стержнях.
Используя ту же модель простой фермы, детали будут такими же, как на предыдущем рисунке, с двумя разными профилями опор. В отличие от совместного метода, здесь нас интересует только нахождение значения сил для элементов BC, EC и ED.
Несколько простых указаний:
- Пропустите секцию через максимум 3 элемента фермы, 1 из которых является нужным элементом, разделяющим ферму на 2 совершенно отдельные части,
- В 1 части фермы определите моменты относительно точки (в стыке), где пересекаются 2 стержня, и определите силу стержня, используя ∑ M = 0,
- Решите два других неизвестных, используя уравнение равновесия для сил, используя ∑ Fx = 0 и ∑ Fy = 0.

Примечание: 3 силы не могут быть одновременными, иначе их нельзя решить.
Виртуальный разрез вводится через единственные обязательные элементы, расположенные вдоль элементов BC, EC и ED. Во-первых, следует определить опорные реакции Ra и Rd. Опять же, для решения этой проблемы требуется здравый смысл, где проще всего было бы рассмотреть либо левую, либо правую сторону. Измерить момент в соединении E (виртуальная точка) по часовой стрелке для всей правой части будет намного проще, чем в соединении C (левая часть). Затем либо соединение D, либо C можно рассматривать как точку момента, либо с помощью метода соединения найти силы в стержнях для FCB, FCE и FDE. Примечание. Каждое значение состояния элемента должно быть четко указано, находится ли он в состоянии растяжения (+ve) или в состоянии сжатия (-ve).
3. Графический метод анализа ферм (диаграмма Максвелла)
Метод соединений может быть использован в качестве основы для графического анализа ферм. Графический анализ был разработан с помощью полигонов сил, начерченных в масштабе для каждого соединения, а затем силы в каждом элементе были измерены по одному из этих полигонов сил. Однако количество линий, которые необходимо нарисовать, можно значительно сократить, если различные силовые полигоны накладываются друг на друга. Полученная диаграмма фермы известна как диаграмма Максвелла.
Графический анализ был разработан с помощью полигонов сил, начерченных в масштабе для каждого соединения, а затем силы в каждом элементе были измерены по одному из этих полигонов сил. Однако количество линий, которые необходимо нарисовать, можно значительно сократить, если различные силовые полигоны накладываются друг на друга. Полученная диаграмма фермы известна как диаграмма Максвелла.
Чтобы напрямую нарисовать диаграмму Максвелла, вот простые рекомендации:
- Решите реакции на опорах, решив уравнения равновесия для всей фермы,
- Двигайтесь по часовой стрелке вокруг внешней стороны фермы; нарисуйте многоугольник силы в масштабе для всей фермы,
- Возьмите каждый сустав по очереди (один за другим), затем нарисуйте многоугольник сил, рассматривая последовательные суставы, на которые действуют только две неизвестные силы,
- Измерьте величину силы в каждом элементе по диаграмме,
- Наконец, обратите внимание, что работа велась от одного конца фермы к другому, так как это используется для проверки баланса и соединения с другим концом.

Простая треугольная ферма с углом наклона θ составляет 60° на каждом угле (равносторонний) и такой же длиной элемента L на 2 типах опор. Опять же, оценка реакции опоры играет важную роль в решении любых структурных задач. В этом случае значение Hb равно нулю, так как на него не влияют никакие горизонтальные силы. Процедура решения этой задачи может быть довольно сложной и требует воображения. Он начинается с маркировки промежутков между силами и стержнями с помощью примера, показанного выше; реакцию Ra и приложенную силу P, обозначенную пробелом 1, и продолжайте движение по часовой стрелке вокруг фермы. Для каждого члена, например, между пробелами 1 и 5 будет член AC и так далее. Примечание. Выберите подходящий масштаб для рисования диаграммы Максвелла.
В заключение, внутренние реакции фермы, а также силы, действующие на ее элементы, можно определить любым из этих трех методов. Тем не менее, метод соединений становится наиболее предпочтительным методом, когда речь идет о более сложных конструкциях.
Для получения дополнительной информации по теме:
☞ Статически определяемые фермы
☞ Решенные примеры для метода соединений для расчета ферм
☞ Анализ ферм
Поставьте лайк и поделитесь этой статьей на facebook:
3 метода анализа ферм Оставьте свои комментарии ниже для любых улучшений или предложений. Мы будем рады разместить ваш ценный вклад.
Опубликовано Engineers Daily в понедельник, 6 июня 2016 г.
Анализ статически неопределимой фермы с использованием метода силы: решенный пример
Введение
Анализ неопределенных ферм обычно выполняется с использованием метода силы или метода прямой жесткости. В этом посте мы шаг за шагом проанализируем анализ фермы, нагруженной, как показано ниже.
(EA = константа)
Решение
Шаг 1 : Определить степень статической неопределенности
Для того, чтобы ферма была детерминированной;
м + r = 2j
Где;
m = количество стержней = 13
r = количество опорных реакций = 4
j = количество соединений = 8
Следовательно;
13 + 4 – 2(8) = 1
Следовательно, ферма неопределима до 1-го порядка по опорам.
Шаг 2: Выберите лишнее и удалите ограничение
Чтобы определить единственную степень неопределенности, конструкция должна быть приведена к статически определимой и устойчивой структуре. Этого можно добиться, удалив лишнюю опору, и небольшое рассмотрение покажет, что для устойчивости конструкции достаточно удалить только лишнюю горизонтальную опору. В этом случае удалим горизонтальную опору в точке H. Это даст нам базовую систему, приведенную ниже.
Шаг 3 : Полный анализ базовой системы и получение внутренних сил
Теперь нам нужно получить опорные реакции и внутренние силы, используя принципы статики.
Опорные реакции
∑M H = 0 (по часовой стрелке)
16Ay – (4 × 12) – (10 × 8) – (5 × 4) – (3 × 2) =
16a y = 154
AY = 9,63 кН
∑M A = 0 (Антиклассница)
16HY — (5 × 12) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 × 8) — (10 °. 4 × 4) + (3 × 2) = 0
4 × 4) + (3 × 2) = 0
16HY = 150
HY = 9,37 кН
∑F x = 0
AY + 3 = 0
AY = -3 КН
Читать также… и проектирование ферм крыши в Eurocode 3
Анализ неопределенных ферм с использованием метода жесткости
Внутренние силы
Совместные A
Geometrical Properties
.0037
θ = TAN -1 (2/4) = 26,57 °
∑F y = 0
-f AC Sinθ +9,63 = 0
F AC = 9,63/SIN 267 °. = 21,53 кН (натяжение)
∑F x = 0
F AB + F AC COSθ -3 = 0
F AB = 3 -(21,53 COS 26,57) = -16,27 кН (кв. Сжатие)
Соединение B
∑F y = 0
-F BC – 4 = 0
F BC = -4kN (Compression)
∑F x = 0
-F AB + F BD = 0
F AB = F BD = -16,27 кН (сжатие)
Чтобы упростить наш анализ, мы можем получить силы в элементах CE и CD с помощью метода сечений.
∑M C = 0
(9,63 × 4) – (3 × 2) + (2 × F BD ) = 0
F BD (проверка сжатия, k=7 BD . наш ответ выше)
∑m D = 0
(9,63 × 8) — (4 × 4)+(2 × F CE ) = 0
F BD = 30,52 кН (Тенсирование)
6. ∑M A = 0
(30,52 × 2) – (4 × 4) + (8 × F CD sinθ) = 0
F CD = -12,59 кН (сжатие) H
∑F y = 0
-F GH sinθ + 9,37 = 0
F GH 0 = 9,37/sin 26,57/sin 26,57/sin5 кН (натяжение)
∑F x = 0
-f FH -F GH COSθ = 0
F FH = -(20,95 COS 26,57) = -18,74 кН (компресса
Совместный E
∑F Y = 0
F ED +0 = 0
F ED = 0 (NO SIGRO)
∑F x = 0
∑F x . CE + F EG = 0
CE + F EG = 0
F CE = F GE = 30,52 кН (растяжение)
Соединение D
∑F y = 0
-f DC SINθ -F DG SINθ -10 = 0
-( -12,59 SINθ) -F DG -0
-(12,59 SINθ) -F DG 4 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10 = 10. 0
F DG = -4,37/sin 26,57° = -9,77 кН (сжатие)
Шаг 4: Рассчитать деформацию в избыточном
Получив внутренние силы в избыточном, мы можем теперь использовать виртуальные метод работы для расчета горизонтального переноса на опоре H, которая соответствует удаленному избыточному Hx. Это делается путем снятия внешней нагрузки с базовой системы и приложения единичной горизонтальной силы в направлении снятой силы.
Глядя на то, что происходит на приведенной выше конструкции, вы согласитесь со мной, что весь верхний пояс испытывает равномерное сжатие -1,0 кН.
Отсюда;
F AB = F BD = F DF = F FH = -1,0 (сжатие)
Все остальные элементы фермы имеют нулевые усилия.
Поскольку горизонтальное смещение в точке H в исходной конструкции равно нулю, это означает, что горизонтальная реакция на опоре H должна вызывать отклонение в противоположном направлении, которое будет противодействовать отклонению.
Деформация базовой системы из-за внешней нагрузки может быть получена с помощью приведенного ниже соотношения;
Где;
м = количество стержней
n = внутренние силы от виртуальной нагрузки
Н = внутренние силы от внешней нагрузки
L = длина стержня
A = площадь поперечного сечения стержня
E = модуль упругости стержня
To проанализировать его, мы обычно представляем это в табличной форме. В связи с тем, что сила в элементах в состоянии виртуальной нагрузки равна нулю во всех элементах, кроме верхнего пояса, мы сосредоточимся только на верхнем поясе.
δ 1P = 2(65,08/AE) + 2(74,96/AE) = 280,08/AE
Прогиб в точке H из-за виртуальной нагрузки может быть получен с использованием того же соотношения, и это показано на Таблица ниже;
δ 11 = 4(4/AE)) = 16/AE
Таким образом, соответствующее каноническое уравнение задается формулой;
δ 11 X 1 + δ 1P = 0
При замене;
16X 1 + 280,08 = 0
X 1 = -17,51 кН ←
Таким образом, горизонтальная реакция в H (Hx) составляет 17,51 кН ←
Получив это, мы можем снова проанализировать ферму, чтобы получить окончательные внутренние силы.
Мы всегда рады видеть вас в Structville.
Вы читали…
Анализ статически неопределимых рам с использованием методов силы и перемещения
Наша интерактивная страница на facebook находится по адресу;
www.facebook.com/structville
1.9: Линии влияния для статически определимых конструкций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 17615
- Феликс Удойо
- Университет Темпл
Глава 9
Линии влияния для статически определяемых конструкций
9. 1 Введение
1 Введение
Такие конструкции, как мосты и мостовые краны, должны быть спроектированы так, чтобы выдерживать движущиеся нагрузки, а также собственный вес. Поскольку конструкции рассчитаны на критические нагрузки, которые могут возникнуть в них, линии влияния используются для определения положения на конструкции, где движущаяся нагрузка вызовет наибольшее напряжение. Линии влияния можно определить как график, ординаты которого показывают изменение величины определенной функции отклика конструкции по мере того, как единичная нагрузка проходит по конструкции. Функции отклика конструкции могут включать осевые силы в элементах, опорные реакции, изгибающие моменты, силы сдвига и прогиб в определенных точках конструкции.
Очень важно подчеркнуть необходимость того, чтобы учащиеся полностью усвоили приведенное выше определение, поскольку большая часть путаницы и трудностей, возникающих при рисовании линий влияния, связана с непониманием разницы между этой темой и изгибающим моментом и поперечным усилием. силовые темы, подробно описанные в четвертой главе. Диаграмма поперечной силы или изгибающего момента показывает величину поперечной силы или изгибающих моментов в различных точках конструкции из-за статических или стационарных нагрузок, действующих на конструкцию, а линии влияния для определенных функций конструкции при заданном Точка конструкции показывает величину этой функции в указанной точке, когда единица движущейся нагрузки пересекает конструкцию. Линии влияния детерминированных структур могут быть получены методом статического равновесия или методом кинематики или Мюллера-Бреслау. Линии влияния по методу статического равновесия называются количественными линиями влияния, так как они требуют некоторых расчетов, а линии влияния по кинематическому методу известны как качественные линии влияния, так как метод позволяет анализатору получить правильную форму линий влияния без любые количественные усилия. В последующих разделах учащиеся рассмотрят, как построить линии влияния для балок и ферм, используя эти два метода.
силовые темы, подробно описанные в четвертой главе. Диаграмма поперечной силы или изгибающего момента показывает величину поперечной силы или изгибающих моментов в различных точках конструкции из-за статических или стационарных нагрузок, действующих на конструкцию, а линии влияния для определенных функций конструкции при заданном Точка конструкции показывает величину этой функции в указанной точке, когда единица движущейся нагрузки пересекает конструкцию. Линии влияния детерминированных структур могут быть получены методом статического равновесия или методом кинематики или Мюллера-Бреслау. Линии влияния по методу статического равновесия называются количественными линиями влияния, так как они требуют некоторых расчетов, а линии влияния по кинематическому методу известны как качественные линии влияния, так как метод позволяет анализатору получить правильную форму линий влияния без любые количественные усилия. В последующих разделах учащиеся рассмотрят, как построить линии влияния для балок и ферм, используя эти два метода.
9.2 Линии влияния для статически детерминированных балок методом статического равновесия
Чтобы понять основную концепцию линий влияния, рассмотрим простую балку, показанную на рис. 9.1а. Статика помогает определить величины реакций на опорах А и В , а перерезывающую силу и изгибающий момент в сечении n , как единичную нагрузку условной единицы, движется справа налево.
Рис. 9.1а. Простой луч.
9.2.1 Реакции пучка
Взяв момент около B , когда единичная нагрузка перемещается на расстояние x от правого конца, можно предположить следующее:
Настройка P = 1 предполагает следующее:
Уравнение 9.2 представляет собой выражение для расчета линии влияния для реакции левого конца свободно опертой балки. Линию влияния для R A можно изобразить графически, поставив некоторые значения x в уравнение. Поскольку уравнение линейное, двух точек должно быть достаточно.
Когда x = 0, R A = 0
Когда x = L , R A = 1
Графическое представление линии влияния для R A показано на рисунке 9.1b, а ордината диаграммы, соответствующая любому значению x , дает величину R A в этот момент.
Рис. 9.1б. Линия влияния для R A .
Аналогично, выражение для линии влияния реакции R B находится, если взять момент около A .
Установка P = 1 в уравнении 9.3 предполагает следующее:
Уравнение 9.4 представляет собой выражение для расчета линии влияния реакции правого конца свободно опертой балки. Подставляя некоторые значения для x в уравнение помогает построить диаграмму линий влияния для R B .
Когда x = 0, R B = 1
Когда x = L , R B = 0
Графическое представление линии влияния для R B показано на рисунке 9. 1c.
1c.
Рис. 9.1c. Линия влияния на Р Б .
9.2.2 Сила сдвига на участке n
Когда единичная нагрузка находится на правой стороне секции, поперечная сила на секции может быть рассчитана с учетом поперечных сил на левой стороне секции следующим образом:
Когда единичная нагрузка находится на левой стороне секции, легче вычислить поперечную силу в секции, учитывая силы на правой стороне секции, следующим образом:
Графическое представление линии влияния поперечной силы в сечении n простой балки показано на рисунке 9.1d.
Рис. 9.1d. Линия влияния на сдвиг на участке n .
9.2.3 Изгибающий момент в сечении n
Когда единичная нагрузка находится на правой стороне секции, изгибающий момент на секции можно рассчитать следующим образом:
Когда единичная нагрузка находится на левой стороне секции, изгибающий момент на секции можно рассчитать следующим образом:
Графическое изображение линии влияния изгибающего момента в сечении n простой балки показано на рисунке 9. 1e.
1e.
Рис. 9.1д. Линия влияния момента на участке n .
9.3 Построение линий влияния
На практике в основном строятся линии влияния, а значения функций определяются геометрией. Процедура построения линий влияния для простых балок, составных балок и ферм будет описана ниже и сопровождается решенным примером для пояснения проблемы. Для каждого случая сразу после схемы будет решаться один пример.
9.3.1 Простые балки с опорой на концах
Процедуры построения линий влияния (I.L.) для некоторых функций балки, опирающейся на оба конца, следующие:
9.3.1.1 Линия влияния левой концевой опоры, R A (рис. 9.2)
(a) В положении левой концевой опоры (точка A ), по оси y- отложите значение +1 (точка A ′).
(b) Нарисуйте линию, соединяющую точку A ′ и нулевую ординату в точке B . Точка B находится в положении опоры B .
(c)Треугольник AA ′ B является линией влияния левой опорной реакции. Идея здесь состоит в том, что когда единичная нагрузка перемещается поперек балки, ее максимальное влияние на реакцию левого конца будет, когда она будет непосредственно лежать на левой концевой опоре. По мере удаления нагрузки от левой концевой опоры ее влияние на левую концевую реакцию будет продолжать уменьшаться до тех пор, пока не достигнет наименьшего значения, равного нулю, когда она лежит непосредственно на правой концевой опоре.
Идея здесь состоит в том, что когда единичная нагрузка перемещается поперек балки, ее максимальное влияние на реакцию левого конца будет, когда она будет непосредственно лежать на левой концевой опоре. По мере удаления нагрузки от левой концевой опоры ее влияние на левую концевую реакцию будет продолжать уменьшаться до тех пор, пока не достигнет наименьшего значения, равного нулю, когда она лежит непосредственно на правой концевой опоре.
Рис. 9.2. Линия влияния для R A .
9.3.1.2 Линия влияния реакции правой концевой опоры R B (рис. 9.3)
(a) На правой концевой опоре (точка B ) начертите ординату со значением +1 (точка B ′).
(b) Проведите линию, соединяющую точку B ′ и точку A.
(c)Треугольник AB ′ B является линией влияния правой концевой реакции опоры. Объяснение линии влияния для реакции опоры на правом конце аналогично объяснению, данному для реакции опоры на левом конце. Максимальный эффект от единичной нагрузки возникает, когда она лежит непосредственно на правой опоре. По мере удаления груза от правой концевой опоры его влияние на реакцию опоры уменьшается до нуля, когда груз непосредственно лежит на левой опоре.
Максимальный эффект от единичной нагрузки возникает, когда она лежит непосредственно на правой опоре. По мере удаления груза от правой концевой опоры его влияние на реакцию опоры уменьшается до нуля, когда груз непосредственно лежит на левой опоре.
Рис. 9.3. Линия влияния для R B .
9.3.1.3 Линия влияния поперечной силы на участке n
(a) На левой концевой опоре (точка A) отложите ординату, равную +1 (точка A ′), как показано на рис. 9.4b.
(b) Нарисуйте линию, соединяющую точку A ′ и нулевую ординату в точке B .
(c) На правой концевой опоре (точка B ) отложите ординату, равную –1 (точка В ′).
(d) Нарисуйте линию, соединяющую B ′ и нулевую ординату в точке A .
(д) Опустить вертикальную линию от рассматриваемого сечения до линий разреза А ′ В и АВ ′ в точках N ′ и N ″ соответственно.
(е) Диаграмма ABN ′ N ″ представляет собой линию влияния поперечной силы на участке n .
(g) Используйте подобный треугольник, чтобы определить ординаты n-N’ и n-N», следующим образом:
Рис. 9.4. Линия влияния сдвига ( b ) и момента ( c ) на сечении м .
9.3.1.4 Линия влияния изгибающего момента на сечении n
(a) На левой концевой опоре (точка A ) отложите ординату со значением, равным расстоянию от левой концевой опоры до сечения n . Например, расстояние a на рис. 9.4c (обозначенное как точка Y на рис. 9)..4с).
(b) Нарисуйте линию, соединяющую точку Y и нулевую ординату в точке B на правой конечной опоре.
(c) Проведите вертикальную линию, проходящую через сечение n и пересекающую линию AZ в точке Q .
(d) Проведите прямую линию AQ , соединяющую A и Q .
(e) Треугольник AQB является линией влияния на данный момент в сечении n . В качестве альтернативы пропустите шаги (b), (c) и (d) и перейдите к шагу (f).
(f) На правой концевой опоре (точка B ) отложите ординату, равную +b. Например, расстояние от правой торцевой опоры до сечения n (обозначается как точка Z ).
(g) Нарисуйте линию, соединяющую Z и нулевую ординату A (положение левой концевой опоры).
(h) На левой концевой опоре (точка A ) отложите ординату, равную +a. Например, расстояние от левой концевой опоры до секции n (обозначается точкой Y ).
(i) Нарисуйте линию, соединяющую Y и нулевую ординату B (положение правой концевой опоры).
(j) Линии AZ и BY пересекаются в точке Q .
(k)Треугольник AQB является линией влияния на данный момент в сечении n . Если точно начертить, с правильным чувством пропорциональности, пересечение Q должно лежать прямо на вертикальной линии, проходящей через сечение n .
(l)Значение ординаты nQ можно получить с помощью подобного треугольника следующим образом:
Пример 9.1
Для двойной выступающей балки, показанной на рис. 9.5а, постройте линии влияния опорных реакций в точках B и C , а также поперечной силы и изгибающего момента в сечении n .
Рис. 9.5. Двойная нависающая балка.
Решение
И.Л. для Б г.
Шаг 1. В положении опоры B (точка B ) отложить ординату +1.
Шаг 2. Проведите прямую линию, соединяющую нанесенную точку (+1) с нулевой ординатой в положении опоры C .
Шаг 3. Продолжите прямую линию шага 2 до конца выступов на обоих концах балки. Линия влияния для B y показана на рис. 9.5b.
Шаг 4. Определить ординаты линии влияния на выступающих концах, используя аналогичный треугольник, следующим образом: для C г.
Шаг 1. В положении опоры С (точка С ) отложить ординату +1.
В положении опоры С (точка С ) отложить ординату +1.
Шаг 2. Проведите прямую линию, соединяющую нанесенную точку (+1) с нулевой ординатой в положении опоры Б .
Шаг 3. Продолжите прямую линию шага 2 до конца выступов на обоих концах балки. Линия влияния для B y показана на рис. 9.5c.
Шаг 4. Определить ординаты линии влияния на выступающих концах, используя аналогичный треугольник, следующим образом: для сдвига Вн.
Шаг 1. В положении опоры B (точка B) отложить ординату +1.
Шаг 2. Проведите прямую линию, соединяющую нанесенную точку (+1) с нулевой ординатой в положении опоры C . Продолжайте прямую линию на C до конца выступа на конце D .
Шаг 3. В положении опоры С (точка С ) отложить ординату –1.
Шаг 4. Проведите прямую линию, соединяющую нанесенную точку (–1) с нулевой ординатой в положении опоры Б . Продолжайте движение по прямой на B до конца выступа на конце A .
Шаг 5. Проведите вертикаль, проходящую через секцию, сдвиг которой необходим для пересечения линий на шаге 2 и шаге 3.
Шаг 6. Соедините точки пересечения, чтобы получить линию влияния, как показано на рис. 9.5d.
Шаг 7. Определите ординаты линий влияния в других точках с помощью подобных треугольников, как показано ранее.
И.Л. на момент М н.
Шаг 1. В точке B отложить ординату, равную +2 м.
Шаг 2. Проведите прямую линию, соединяющую ординату, нанесенную на шаге 1, с нулевой ординатой в опоре C .
Шаг 3. В точке C отложить ординату, равную +2 м.
Шаг 4. Нарисуйте прямую линию, соединяющую ординату, нанесенную на шаге 3, с нулевой ординатой на опоре B .
Шаг 5. Продолжите прямые линии от пересечения линий, проведенных в шагах 2 и 4, через опоры к выступающим концам, как показано на рис. 9.5е.
Шаг 6. Определите значения линий влияния в других точках с помощью подобных треугольников, как показано ранее.
Пример 9.2
Для балки с выступающей опорой В одним концом, как показано на рисунке 9.6, постройте линии влияния изгибающего момента на опоре В , поперечной силы на опоре В , опорных реакций на В и С , а поперечная сила и изгибающий момент в сечении « к ».
Рис. 9.6. Балка с одной выступающей опорой.
Решение
Линии влияния в примере 9.2 для желаемых функций были построены на основе процедуры, описанной в предыдущем разделе и примере.
9.3.2 Составные балки
Чтобы правильно нарисовать линию влияния для любой функции составной балки, необходимо хорошее понимание взаимодействия элементов балки, как обсуждалось в главе 3, раздел 3.3. Студент должен вспомнить из предыдущего раздела, что составная балка состоит из основной конструкции и дополнительной конструкции. Два изложенных ниже факта необходимо всегда помнить, так как от них зависит степень распространения линии влияния составных лучей. Запоминание этих фактов также послужит временной проверкой правильности проведенной линии влияния.
Запоминание этих фактов также послужит временной проверкой правильности проведенной линии влияния.
Нагрузка подвижной единицы будет влиять на функции основной конструкции, когда она расположена в любой точке, не только на основной конструкции, но и на дополняющей конструкции, поскольку последняя создает нагрузку на первую.
Нагрузка на движущуюся единицу будет влиять только на функции дополняющей конструкции, когда она расположена внутри дополняющей конструкции; это не повлияет ни на одну функцию дополнительной структуры, если она находится в любой точке первичной структуры.
Вышеизложенные факты будут продемонстрированы на следующих примерах.
Пример 9.3
Для составной балки, показанной на рис. 9.7, постройте линии влияния и укажите критические ординаты для опорных реакций в точках A , B и D , изгибающего момента в точке B и сдвига в шарнире. С .
Рис. 9.7. Составной луч.
Решение
Перед построением линий влияния для желаемых функций необходимо сначала наблюдать протяженность линий влияния на схематической диаграмме взаимодействия элементов, как показано на рисунке 9..7б.
И.Л. для А и . Реакция A y является функцией основной конструкции, поэтому единичная нагрузка будет влиять на эту функцию, когда она находится в любой точке балки, как было указано ранее в разделе 9.3.2. С учетом этого постройте линию влияния A y следующим образом:
Шаг 1. В точке A начертите ординату +1.
Шаг 2. Нарисуйте прямую линию, соединяющую ординату, нанесенную на шаге 1, с нулевой ординатой в опоре B , и продолжайте эту линию до конца выступающего конца основной конструкции, как показано на схеме взаимодействия.
Шаг 3. Проведите прямую линию, соединяющую ординату в конце выступа с нулевой ординатой на опоре D . Линия влияния показана на рис. 9.7c.
Линия влияния показана на рис. 9.7c.
Шаг 4. Используйте аналогичный треугольник для вычисления ординат линии влияния
И.Л. для B и . Линия влияния этой реакции будет охватывать всю длину балки, поскольку она является опорной реакцией в первичной конструкции. Зная это, постройте линию влияния для B y следующим образом:
Шаг 1: В точке B начертите ординату +1.
Шаг 2. Проведите прямую линию, соединяющую ординату, нанесенную на шаге 1, с нулевой ординатой в опоре A . Продолжить линию в поддержку B до конца выступающего конца основной конструкции, как показано на схеме взаимодействия.
Шаг 3. Проведите прямую линию, соединяющую ординату выступающего конца с нулевой ординатой на опоре D . Линия влияния для B y показана на рис. 9.7d.
Шаг 4. С помощью аналогичного треугольника определить значения ординаты линии влияния.
И. Л. для D и . Реакция D y является функцией дополнительной конструкции, и на нее будет влиять, если единичная нагрузка находится в любой точке дополнительной конструкции. На него не повлияет, если единичная нагрузка пересекает первичную конструкцию, как указано в разделе 9.3.2. Таким образом, протяженность линии влияния будет равна длине комплементарной структуры. Зная это, проведите линию влияния для D y .
Л. для D и . Реакция D y является функцией дополнительной конструкции, и на нее будет влиять, если единичная нагрузка находится в любой точке дополнительной конструкции. На него не повлияет, если единичная нагрузка пересекает первичную конструкцию, как указано в разделе 9.3.2. Таким образом, протяженность линии влияния будет равна длине комплементарной структуры. Зная это, проведите линию влияния для D y .
Шаг 1. В точке D начертите ординату +1.
Шаг 2. Нарисуйте прямую линию, соединяющую ординату, нанесенную на шаге 1, с нулевой ординатой шарнира C . Линия влияния для D y показана на рис. 9.7e.
Линии влияния момента B и сдвига C показаны на рис. 9.7f и рис. 9.7g соответственно.
Пример 9.4
Для составной балки, показанной на рис. 9.8а, постройте линии влияния и укажите критические ординаты для опорных реакций в точке 9.0582 F и G , поперечная сила и изгибающий момент в D и момент в F .
Рис. 9.8. Составной луч.
Решение
На рисунках с 9.8c по 9.8g показаны линии влияния для желаемых функций. Схематическая диаграмма взаимодействия элементов, показанная на рис. 9.8b, неизмеримо помогает первоначальному восприятию диапазона линии влияния каждой функции. Построение линий влияния следует описанию, изложенному в предыдущих разделах.
9.3.3 Линии влияния для балок, поддерживающих системы перекрытий
До сих пор в примерах и тексте рассматривались только случаи, когда нагрузка подвижного элемента приложена непосредственно к конструкции. Но на практике это может быть не всегда. Например, иногда нагрузки от перекрытий зданий или мостовых перекрытий передаются через второстепенные балки, такие как стрингеры и поперечные балки, на балки, поддерживающие систему перекрытий здания или моста, как показано на рис. 9.9. Колонны, причалы или опоры, в свою очередь, поддерживают балки.
Рис. 9.9. Передача нагрузки на ферму системой стрингеров и балок перекрытий.
Как показано на рис. 9.9, автомобильная нагрузка от настила моста передается на балку в точках 1, 2, 3, 4 и 5, называемых точками панели, где балки перекрытий соприкасаются с балкой. Сегмент между двумя последовательными контактными точками называется панелью. Для иллюстрации конструкции линий влияния в случае косвенного приложения нагрузок балки перекрытий и ферма на рис. 9.9 отделены от всей системы, как показано на рисунке 9.10. Предположим, что длина каждой панели равна 4 м. Постройте линии влияния момента в точке 4 и момента и сдвига в сечении n в средней точке 3 и 4 (точка, лежащая в пределах панели 3-4). Линия влияния для момента в точке 4 показана на рис. 9.10б; обратите внимание, что построение линии влияния момента в этой точке точно такое же, как и в случаях, рассмотренных в предыдущих разделах, где подвижная нагрузка приложена непосредственно к балке. Когда единичная нагрузка перемещается вправо от 4 и влево от 3, линия влияния на данный момент для любого сечения в пределах панели 3-4 будет постоянной, как показано на рисунке 9. .10с. Построение линии влияния на сдвиг любого сечения в пределах панели 3-4 получается таким же образом, как и при прямом воздействии единичной нагрузки на балку, за исключением того, что проводится диагональная линия, соединяющая точки, в которых вертикальная линия, проведенная из точек, пересекается с линией построения.
.10с. Построение линии влияния на сдвиг любого сечения в пределах панели 3-4 получается таким же образом, как и при прямом воздействии единичной нагрузки на балку, за исключением того, что проводится диагональная линия, соединяющая точки, в которых вертикальная линия, проведенная из точек, пересекается с линией построения.
Рис. 9.10. Линии влияния в случае непрямого приложения нагрузок.
Пример 9.5
Нарисуйте линии влияния на данный момент в C и сдвиг панели BC балки перекрытия, показанной на рис. 9.11.
Рис. 9.11а. Половая балка.
Решение
Линия влияния для M C . Чтобы получить значения линии влияния M C , последовательно приложите нагрузку 1 кН в точках панели A , B , C , D и E . Для определения момента используйте уравнение статики. Значения M C в соответствующих точках панели представлены в таблице 9. 1. Когда единичная нагрузка расположена на B , как показано на рисунке 9.11b, значение M C определяется следующим образом:
1. Когда единичная нагрузка расположена на B , как показано на рисунке 9.11b, значение M C определяется следующим образом:
Рис. 9.11b. Единичная нагрузка на B .
Сначала определите опорные реакции в балке, используя уравнение статического равновесия.
Затем по рассчитанной реакции определить M C следующим образом:
М с = 0,25(12) = 3 кН – м
Таблица 9.1. Значения M C в соответствующих точках панели.
Рис. 9.11c. Линия влияния для M C .
Линия влияния для V BC . Для получения значений линии влияния МВ ВС последовательно располагают нагрузку 1 кН в точках панели А , B , C , D и E . Для определения поперечной силы используйте уравнение статики. Значения В С в соответствующих точках панели представлены в таблице 9. 2.
2.
Таблица 9.2. Значения V C в соответствующих точках панели.
Рис. 9.11d. Линия влияния для V BC .
9.3.4 Линии влияния для ферм
Процедура построения линий влияния для стержневых элементов аналогична процедуре построения балки, поддерживающей систему перекрытий, рассмотренной в разделе 9..3.3. Нагрузки на элементы фермы могут передаваться через узлы верхней или нижней панели. На рис. 9.12 нагрузка передается на стержни через узлы верхней панели. По мере того, как временные нагрузки перемещаются по ферме, они передаются на узлы верхней панели поперечными балками и косоурами. Линии влияния осевых усилий в элементах фермы можно построить, соединив ординаты линий влияния в узлах панелей прямыми линиями.
Рис. 9.12. Нагрузка передается системой стрингеров и поперечных балок.
Чтобы проиллюстрировать процедуру построения линий влияния для ферм, рассмотрим следующие примеры.
Пример 9.6
Нарисуйте линии влияния для реакций A y , F y и для осевых усилий в элементах CD , HG и CG нагрузка перемещается поперек вершины нагрузки как единое целое фермы, как показано на рисунке 9.13.
Рис. 9.13. Ферма.
Решение
Чертеж линий влияния для ферм аналогичен рисунку балки. Первый шаг к рисованию линий влияния осевых сил в указанных элементах состоит в том, чтобы провести воображаемое сечение через элементы, как показано на рисунке 9.13b, и применить равновесие к части по обе стороны от сечения. Пошаговая процедура построения линии влияния для каждого из членов изложена ниже.
Линия влияния осевой силы в элементе CD . Когда единичная нагрузка находится в любой точке справа от D , учитывая равновесие левого сегмента AH (рис. 9.13в), напрашивается следующее: свидетельствует о том, что линия влияния для F CD на участке DE может быть определена путем умножения соответствующего участка линии влияния для реакции A y на – 2. Линия влияния для A y показан на рис. 9.13e.
Линия влияния для A y показан на рис. 9.13e.
При расположении единичной нагрузки в любой точке слева от С , учитывая равновесие правого отрезка ГФ (рис. 9.13г), следует следующее:
Полученное выражение F CD в терминах F y свидетельствует о том, что линия влияния для F CD в части AH может быть определена путем умножения соответствующей части линии влияния для реакция F y по – 1. Линия влияния для F y показана на рис. 9.13f.
Линия влияния осевой силы в элементе CD , построенная из линий влияния реакций A y и F y , показана на рис. 9.13g.
Линия влияния для элемента HG . Когда единичная нагрузка находится в любой точке справа от D , учитывая равновесие левого сегмента AH (рис. 9.13в), из него следует следующее:
Из полученного выражения F HG через A y следует, что линия влияния часть DE идентична части A и в пределах соответствующего сегмента.
Когда единичная нагрузка находится в любой точке слева от C , с учетом равновесия правого сегмента 9
Полученное выражение F HG через F y свидетельствует о том, что линия влияния F HG в части AH можно определить путем умножения соответствующей части линии влияния реакции F y на 2.
Линия влияния осевой силы в элементе HG , построенная по линии влияния реакций A y и F y , также показана на рис. 9.13h.
Линия влияния осевой силы в стержне CG . Когда единичная нагрузка находится в любой точке справа от D , с учетом равновесия левого отрезка AH (рис. 9.13C) получается следующее:
Полученное выражение F КГ , со ссылкой на A y , подразумевает, что линия влияния для F CG в части DE может быть определена путем умножения соответствующей части линии влияния для реакции A y на 1. 41.
41.
Когда единичная нагрузка находится в любой точке слева от C , с учетом равновесия правого сегмента GF (рис. 9.13d) получается следующее:
Полученное выражение F CG через F y свидетельствует о том, что линия влияния F CG на участке может быть определена перемножением соответствующей 3AH участок линии влияния реакции F y by – 1,41.
Линия влияния осевой силы в элементе CG , построенная из линии влияния реакций A y и F y показан на рис. 9.13i.
Пример 9.7
Нарисуйте линии влияния силы в элементе CH при перемещении единичной нагрузки по верхней части фермы, как показано на рис. 9.14а.
Рис. 9.14. Ферма.
Решение
Чтобы получить выражение для линии влияния осевой силы в элементе CH , сначала проведите воображаемое сечение, проходящее через этот элемент, как показано на рисунке 9. .14а.
.14а.
При расположении единичной нагрузки в любой точке справа от G , учитывая равновесие левого отрезка AH (рис. 9.14 C), следует следующее:
Полученное выражение F CH в пересчете на A y указывает, что линия влияния для F CH в части AH может быть определена путем умножения соответствующей части линии влияния для реакции A y by – 1.
При расположении единичной нагрузки в любой точке слева от H , учитывая равновесие правого отрезка GF (рис. 9.14d), следует следующее
Полученная экспрессия F CH С точки зрения F y , подразумевает, что линия влияния для F CH на порции GF 333. у в соответствующем сегменте.
Линия влияния CG показана на рис. 9.14ж.
9.4 Использование линий влияния
9.4.1 Использование линий влияния для определения функций отклика конструкций, подвергающихся сосредоточенным нагрузкам
Величина функции отклика конструкции из-за сосредоточенных нагрузок может быть определена как сумма произведения соответствующих нагрузок и соответствующих ординат линии влияния для этой функции отклика. Пример 9.5 и пример 9.6 иллюстрируют такие случаи.
Пример 9.5 и пример 9.6 иллюстрируют такие случаи.
Пример 9.8
Простая балка подвергается воздействию трех сосредоточенных нагрузок, как показано на рис. 9.15а. Определить величины реакций, поперечную силу и изгибающий момент в средней точке балки с помощью линий влияния.
Рис. 9.15. Простой луч.
Решение
Сначала начертите линию влияния опорных реакций, поперечной силы и изгибающего момента в средней точке балки (см. рис. 9)..15b, рис. 9.15c, рис. 9.15d и рис. 9.15e). После того, как линии влияния для функций нарисованы, вычислите величину функций отклика следующим образом:
Величина реакций поддержки, используя диаграммы линий влияния на рис. 9.15b и рис. 9.15c.
Величина поперечной силы в сечении n с использованием диаграммы линии влияния на рисунке 9.15d.
Величина изгибающего момента в сечении n , используя диаграмму линии влияния на рисунке 9.15e.
Пример 9. 9
9
Составная балка подвергается воздействию трех сосредоточенных нагрузок, как показано на рис. 9.16а. Используя линии влияния, определите величины сдвига и момента в точке A и реакции опоры в точке D .
Рис. 9.16. Составной луч.
Решение
Сначала начертите линию влияния поперечной силы V A , изгибающий момент M A и реакция C y . Линии влияния для этих функций показаны на рис. 9.16b, рис. 9.16c и рис. 9.16d. Затем вычислите величину этих функций отклика следующим образом:
Величина сдвига в секции n , используя диаграмму линии влияния на рисунке 9.16b.
Величина изгибающего момента в сечении n с использованием диаграммы линии влияния на рисунке 9.16c.
Величина реакции поддержки C y с использованием диаграммы линий влияния на рис. 9.16d.
9.4.2 Использование линий влияния для определения функций отклика конструкций, подверженных распределенным нагрузкам
Величина функции отклика конструкции, подверженной распределенным нагрузкам, может быть определена как произведение интенсивности распределенной нагрузки и площади линии влияния. Рассмотрим балку, на которую действует равномерная нагрузка 9.0582 ω x , как показано на рисунке 9.17а. Сначала преобразуйте равномерную нагрузку в эквивалентную сосредоточенную нагрузку. Эквивалентная элементарная сосредоточенная нагрузка для распределенной нагрузки, действующей на длину дифференциала dx , выглядит следующим образом:
Рассмотрим балку, на которую действует равномерная нагрузка 9.0582 ω x , как показано на рисунке 9.17а. Сначала преобразуйте равномерную нагрузку в эквивалентную сосредоточенную нагрузку. Эквивалентная элементарная сосредоточенная нагрузка для распределенной нагрузки, действующей на длину дифференциала dx , выглядит следующим образом:
Величина функции отклика ( rf ) из-за элементарной сосредоточенной нагрузки, действующей на конструкцию, может быть выражена следующим образом:
где
y = ордината линии влияния в точке приложения нагрузки дП .
Рис. 9.17. Балка подвергается равномерной нагрузке.
Суммарная функция отклика ( RF ) из-за распределенной нагрузки, действующей на сегмент BC балки, получается путем интегрирования следующим образом:
Интеграл представляет собой площадь под участком линии влияния, соответствующей нагруженному участку балки (см. заштрихованную область на рис. 9.17б).
заштрихованную область на рис. 9.17б).
Пример 9.10
Используя линии влияния, определите поперечную силу и изгибающий момент в средней точке нагруженной простой балки, как показано на рисунке 9..18а.
Рис. 9.18. Нагруженная простая балка.
Решение
Сначала начертите линию влияния поперечной силы и изгибающего момента в середине пролета балки. Линии влияния для этих функций показаны на рис. 9.18b и рис. 9.18c. Затем вычислите величину этих функций отклика следующим образом:
Из диаграммы линий влияния, показанной на рис. 9.18b, величина сдвига в точке B выглядит следующим образом:
Величина изгибающего момента в точке B , используя линейную диаграмму влияния на рисунке 9.18c, выглядит следующим образом:
Пример 9.11
Составная балка подвергается комбинированной нагрузке, как показано на рис. 9.19а. Используя линии влияния, определить величины реакций на опорах A , B , и C .
Рис. 9.19. Составная балка, подвергаемая комбинированному нагружению.
Раствор
Величина реакции поддержки A y , используя диаграмму линии влияния на рисунке 9.19b.
Величина реакции опоры B y , используя диаграмму линии влияния на рис. 9.19c.
Величина реакции опоры D y , используя диаграмму линии влияния на рис. 9.19d.
9.4.3 Использование линий влияния для определения максимального воздействия в точке из-за движущихся сосредоточенных нагрузок
При анализе и проектировании конструкций, таких как мосты и краны, подверженные подвижным нагрузкам, часто желательно найти положение подвижных нагрузок, которое будет оказывать максимальное влияние в точке. Для некоторых структур это можно определить путем простого осмотра, в то время как для большинства других может потребоваться процесс проб и ошибок с использованием линий влияния. Примеры 9. 12 и 9.13 иллюстрируют процесс проб и ошибок, связанный с использованием линий влияния для вычисления величины некоторых функций балки, подвергаемой серии сосредоточенных движущихся нагрузок.
12 и 9.13 иллюстрируют процесс проб и ошибок, связанный с использованием линий влияния для вычисления величины некоторых функций балки, подвергаемой серии сосредоточенных движущихся нагрузок.
Пример 9.12
Используя линии влияния, определите поперечную силу и изгибающий момент в средней точке k балки, показанной на рис. 9.20а. На балку действует серия движущихся сосредоточенных нагрузок, показанных на рис. 9.20б.
Рис. 9.20. Луч.
Решение
Максимальный сдвиг В k из рис. 9.20c.
Максимальный положительный сдвиг = 7,8 к
Максимальный отрицательный сдвиг = 9,3 k
Максимальный момент M k из рисунка 9.20d.
Пример 9.13
Составная балка, показанная на рис. 9.21а, подвергается действию ряда движущихся сосредоточенных нагрузок, которые показаны на рис. 9.21б. По линиям влияния определить величины реакций опор А , В и С и изгибающий момент в сечении n .
Рис. 9.21. Составной луч.
Раствор
9.4.4 Использование линий влияния для определения абсолютной максимальной функции отклика в любой точке конструкции
В предыдущих разделах объясняется использование линий влияния для определения максимальной функции отклика, которая может возникнуть в определенных точках конструкции. В этом разделе объясняется определение абсолютного максимального значения функции отклика, которое может возникнуть в любой точке всей конструкции из-за сосредоточенных нагрузок, создаваемых движущимися нагрузками.
Абсолютная максимальная сила сдвига для консольной балки возникает в точке рядом с закрепленным концом, а для свободно опертой балки возникает вблизи одной из ее реакций. Абсолютный максимум момента для консольной балки также будет иметь место вблизи неподвижного конца, в то время как момент для свободно опертой балки неизвестен и, таким образом, потребует некоторого анализа. Чтобы найти положение, в котором возникает абсолютный максимальный момент в свободно опертой балке, рассмотрим балку, на которую действуют три движущиеся сосредоточенные нагрузки 9. 0582 P 1 , P 2 и P 3 , как показано на рис. 9.22.
0582 P 1 , P 2 и P 3 , как показано на рис. 9.22.
Хотя из статики известно, что абсолютный максимальный момент возникнет при одной из сосредоточенных нагрузок, необходимо определить конкретную нагрузку, при которой он возникнет, и его расположение вдоль балки. Сосредоточенная нагрузка, при которой возникнет абсолютный максимальный момент, может быть определена осмотром или методом проб и ошибок, но местоположение этой нагрузки должно быть установлено аналитически. Предположим, что сосредоточенная нагрузка, при которой возникнет абсолютный максимальный момент, равна P 3 , а расстояние P 3 от центральной линии луча составляет x . Чтобы получить выражение для x , сначала определите равнодействующую P R сосредоточенных нагрузок, действующих на расстоянии x ′ от нагрузки P 3 .
Чтобы определить правильную реакцию балки, возьмите момент относительно опоры A следующим образом:
Рис. 9.22. На балку действуют три движущиеся сосредоточенные нагрузки.
9.22. На балку действуют три движущиеся сосредоточенные нагрузки.
Чтобы определить правильную реакцию балки, возьмите момент относительно опоры A следующим образом:
Таким образом, изгибающий момент при М 3 равен:
Расстояние x , для которого M 3 является максимальным, можно определить, продифференцировав уравнение 9.9 по отношению к x и приравняв его нулю, следующим образом:
Следовательно,
Из уравнения 9.10 следует, что абсолютный максимальный момент в свободно опертой балке возникает под действием одной из сосредоточенных нагрузок, когда нагрузка, при которой возникает момент, и равнодействующая системы нагрузок равноудалены от центра балки.
Пример 9.14
Определите абсолютный максимальный изгибающий момент в свободно опертом балочном мосту длиной 16 м, нагруженном движущимся грузовиком, как показано на рисунке 9. .23.
.23.
Рис. 9.23. Балка с простой опорой.
Решение
Используя статику, сначала определите значение и положение равнодействующей движущихся нагрузок.
Результирующая нагрузка.
Положение равнодействующей нагрузки. Для определения положения равнодействующей нагрузки принимают момент относительно точки n , которая находится непосредственно под нагрузкой 20 кН, следующим образом:
Рис. 9.24. Результирующая и нагрузка равноудалены от осевой линии балки.
Если предполагается, что абсолютный максимальный момент возникает при нагрузке 50 кН, расположение равнодействующей и этой нагрузки на равном расстоянии от осевой линии балки показано на рис. 9.24. Перед вычислением абсолютного максимального момента сначала определите реакцию B y с помощью статики.
Абсолютный максимальный момент при нагрузке 50 кН:
M 50 = (92,2)(9,22) – (90)(3,78) = 509,88 кН. м
м
Рис. 9.25. Результирующая и нагрузка равноудалены от осевой линии балки.
Если предполагается, что абсолютный максимальный момент возникает при нагрузке 90 кН, то расположение равнодействующей и этой нагрузки на равном расстоянии от центральной линии балки будет таким, как показано на рис. 9.25.
Перед вычислением абсолютного максимального момента сначала определите реакцию B y с помощью статики.
Абсолютный максимальный момент под 9Нагрузка 0 кН выглядит следующим образом:
Из двух возможных случаев, рассмотренных в решении, видно, что абсолютный максимум момента возникает при усилии 50 кН.
Краткое изложение главы
Линии влияния для статически определимых конструкций: Влияние подвижной нагрузки на величину некоторых функций конструкции, таких как опорные реакции, прогиб, поперечная сила и момент, в сечении конструкции зависят от положения подвижная нагрузка. Линии влияния используются для изучения максимального влияния движущейся нагрузки на эти функции в целях проектирования. Линии влияния для определенных структур могут быть получены методом статического равновесия или методом кинематики или Мюллера-Бреслау. Линии влияния первого метода могут быть определены количественно, тогда как линии влияния второго метода могут быть получены качественно, как было показано в этой главе. Решается несколько примеров задач, показывающих, как построить линии влияния для балок и ферм с использованием вышеизложенных методов.
Линии влияния для определенных структур могут быть получены методом статического равновесия или методом кинематики или Мюллера-Бреслау. Линии влияния первого метода могут быть определены количественно, тогда как линии влияния второго метода могут быть получены качественно, как было показано в этой главе. Решается несколько примеров задач, показывающих, как построить линии влияния для балок и ферм с использованием вышеизложенных методов.
Практические задачи
9.1 Нарисуйте линию влияния поперечной силы и момента в сечении n в середине пролета свободно опертой балки, показанной на рисунке P9.1.
Рис. P9.1. Просто поддерживаемая балка.
9.2 Нарисуйте линии влияния реакции в точках A и B , а также сдвига и изгибающего момента в точке C балки с выступающими концами, как показано на рисунке P9.2.
Рис. P9.2. Балка с навесом.
9.3 Начертите линию влияния реакций на опору консольной балки, показанную на рисунке P9. 3.
3.
Рис. P9.3. Консольная балка.
9.4 Начертите линию влияния опорных реакций в точках B и D , а также поперечных и изгибающих моментов в сечении n балки, показанной на рис. 9.4.
Рис. P9.4. Луч
9.5 Начертите линии влияния опорных реакций на C и D и в точке B составной балки, показанной на рисунке P9.5.
Рис. P9.5. Составной луч.
9.6 Начертите линии влияния поперечной силы и момента в сечениях n s и k составной балки, показанной на рисунке P9.6.
Рис. P9.6. Составной луч.
9.7 Определите абсолютный максимальный изгибающий момент в свободно опертом балочном мосту длиной 65 футов, подверженном нагрузке движущегося грузовика, как показано на рисунке P9..7.
Рис. P9.7. Просто опертый балочный мост.
9.8 Определите абсолютный максимальный изгибающий момент в свободно опертом балочном мосту длиной 12 м, нагруженном движущимся грузовиком, как показано на рисунке P9. 8.
8.
Рис. P9.8. Просто опертый балочный мост.
9.9 Определите абсолютный максимальный изгибающий момент в свободно опертом балочном мосту длиной 40 футов, нагруженном движущимся грузовиком, как показано на рисунке P9.9.
Рис. P9.9. Просто опертый балочный мост.
9.10 Определите абсолютный максимальный изгибающий момент в свободно опертом балочном мосту длиной 14 м, нагруженном движущимся грузовиком, как показано на рисунке P9.10.
Рис. P9.10. Просто опертый балочный мост.
9.11 Начертите линии влияния момента B и поперечной силы в панели CD балки перекрытия, показанной на рисунке P9.11.
Рис. P9.11. Половая балка.
9.12 Начертите линии влияния момента C и поперечной силы в панели BC балки перекрытия, показанной на рисунке P9.12.
Рис. P9.12. Половая балка.
9.13 Нарисуйте линии влияния момента в точке B и сдвига в панели CD балки перекрытия, показанной на рисунке P9. 13.
13.
Рис. P9.13. Половая балка.
9.14 Нарисуйте линии влияния на данный момент в D и усилие сдвига в панели DE балки перекрытия, показанной на рисунке P9.14.
Рис. P9.14. Половая балка.
9.15 Начертите линии влияния момента в точке D и поперечной силы в панели AB балки перекрытия, показанной на рисунке P9.15.
Рис. P9.15. Половая балка.
9.16 Начертите линии влияния сил в элементах CD , CF и GF , когда единичная нагрузка перемещается по верху фермы, как показано на рисунке P9.16.
Рис. P9.16. Ферма.
9.17 Начертите линии влияния усилий в элементах DE , NE и NM , когда единичная динамическая нагрузка передается на верхние пояса фермы, как показано на рисунке P9.17.
Рис. P9.17. Ферма.
9.18 Начертите линии влияния сил в стержнях DE , DH , IH и HG , поскольку единичная динамическая нагрузка передается на нижние пояса фермы, как показано на рисунке P9. 18.
18.
Рис. P9.18. Ферма.
9.19 Нарисуйте линии влияния усилий в элементах BC , BF , FE и ED при перемещении единичной нагрузки по нижнему поясу фермы, как показано на рисунке P9.19.
Рис. P9.19. Ферма.
Эта страница под названием 1.9«Линии влияния для статически определяемых структур» распространяются под лицензией CC BY-NC-ND 4.0, автором, ремиксом и/или куратором является Феликс Удоэйо с использованием исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Феликс Удоэйо
- Лицензия
- CC BY-NC-ND
- Версия лицензии
- 4,0
- Теги
- источник@https://temple.
 manifoldapp.org/projects/structural-analysis
manifoldapp.org/projects/structural-analysis
- источник@https://temple.
Ферма — Словарь героев Википедии
Чтобы узнать о других значениях, см. Ферма (значения).
Ферменный мост для однопутной железной дороги, переоборудованный для пешеходного движения и опоры трубопровода. В этом примере ферма представляет собой группу треугольных элементов, поддерживающих мост.
Типовая деталь стальной фермы, которая рассматривается как вращательное соединение
Историческая деталь стальной фермы с фактическим вращательным соединением
Ферма представляет собой сборку из элементов , таких как балки, соединенные узлами , что создает жесткую конструкцию. [1]
В машиностроении ферма — это конструкция, которая «состоит только из элементов с двумя силами, где элементы организованы так, что сборка в целом ведет себя как единый объект». [2] «Элемент двух сил» представляет собой конструктивный элемент, в котором сила приложена только к двум точкам. Хотя это строгое определение позволяет элементам иметь любую форму, соединенную в любой устойчивой конфигурации, фермы обычно состоят из пяти или более треугольных элементов, построенных из прямых элементов, концы которых соединены в соединениях, называемых 9.0582 узлов .
[2] «Элемент двух сил» представляет собой конструктивный элемент, в котором сила приложена только к двум точкам. Хотя это строгое определение позволяет элементам иметь любую форму, соединенную в любой устойчивой конфигурации, фермы обычно состоят из пяти или более треугольных элементов, построенных из прямых элементов, концы которых соединены в соединениях, называемых 9.0582 узлов .
В этом типичном контексте считается, что внешние силы и реакции на эти силы действуют только в узлах и приводят к силам в элементах, которые являются либо растягивающими, либо сжимающими. Для прямых элементов моменты (крутящие моменты) явно исключены, потому что и только потому, что все соединения в ферме рассматриваются как вращающиеся, что необходимо для того, чтобы звенья были элементами с двумя силами.
В плоской ферме все элементы и узлы лежат в двухмерной плоскости, а в пространственной ферме элементы и узлы простираются в трех измерениях. Верхние балки фермы называются 9. 0582 верхних поясов и обычно находятся в состоянии сжатия, нижние балки называются нижними поясами и обычно находятся в состоянии растяжения. Внутренние балки называются полотнами , а области внутри полотен называются панелями , [3] или из графической статики (см. диаграмму Кремоны) полигонами . [4]
0582 верхних поясов и обычно находятся в состоянии сжатия, нижние балки называются нижними поясами и обычно находятся в состоянии растяжения. Внутренние балки называются полотнами , а области внутри полотен называются панелями , [3] или из графической статики (см. диаграмму Кремоны) полигонами . [4]
Содержание
- 1 Этимология
- 2 Характеристики
- 2.1 Простая ферма
- 2.2 Planar truss
- 2.3 Space frame truss
- 3 Types
- 3.1 Warren truss
- 3.2 Octet truss
- 3.3 Pratt truss
- 3.4 Bowstring truss
- 3.5 King post truss
- 3.6 Lenticular truss
- 3.7 Решетчатая ферма города
- 3.8 Ферма Виренделя
- 4 Статика
- 5 Расчет
- 5.1 Силы в элементах
- 5.2 Расчет элементов
- 5.3 Design of joints
- 6 Applications
- 6.
 1 Post frame structures
1 Post frame structures
- 6.
- 7 Gallery
- 8 See also
- 9 References
- 10 External links
Etymology[edit]
Truss derives от старофранцузского слова trousse , примерно 1200 г., что означает «собрание связанных вместе вещей». [5] [6] Термин ферма часто используется для описания любой сборки элементов, таких как рама [7] [8] или пару стропил. [9] [10] Одно инженерное определение: «Ферма представляет собой единую плоскую конструкцию из отдельных конструктивных элементов [так в оригинале], соединенных на своих концах в виде ряда треугольников [так в оригинале], охватывающих большое расстояние». [11]
Характеристики[править]
Египетское судно с веревочной фермой — старейшее известное использование ферм. Фермы не вошли в обиход до римской эпохи.
Ферма состоит из обычно (но не обязательно) прямых элементов, соединенных в узлах, традиционно называемых точки панели . Фермы обычно (но не обязательно [12] ) состоят из треугольников из-за структурной стабильности этой формы и конструкции. Треугольник — простейшая геометрическая фигура, которая не меняет форму при фиксированных длинах сторон. [13] Для сравнения, и углы, и длины четырехсторонней фигуры должны быть фиксированными, чтобы она сохраняла свою форму. Соединение, на которое должна опираться ферма, обычно называют точкой Мунтера. [ цитирование требуется ]
Фермы обычно (но не обязательно [12] ) состоят из треугольников из-за структурной стабильности этой формы и конструкции. Треугольник — простейшая геометрическая фигура, которая не меняет форму при фиксированных длинах сторон. [13] Для сравнения, и углы, и длины четырехсторонней фигуры должны быть фиксированными, чтобы она сохраняла свою форму. Соединение, на которое должна опираться ферма, обычно называют точкой Мунтера. [ цитирование требуется ]
Простая ферма Этот тип фермы можно увидеть в каркасной крыше, состоящей из стропил и потолочной балки,
[14] , а также в других механических конструкциях, таких как велосипеды и самолеты. Из-за стабильности этой формы и методов анализа, используемых для расчета сил внутри нее, ферма, полностью состоящая из треугольников, известна как простая ферма. [15] Однако простая ферма часто определяется более строго, требуя, чтобы ее можно было сконструировать путем последовательного добавления пар элементов, каждый из которых соединяется с двумя существующими соединениями и друг с другом для образования нового соединения, и это определение не не требует, чтобы простая ферма состояла только из треугольников. [12] Традиционная велосипедная рама ромбовидной формы, в которой используются два соединенных треугольника, является примером простой фермы. [16]
[12] Традиционная велосипедная рама ромбовидной формы, в которой используются два соединенных треугольника, является примером простой фермы. [16] Плоская ферма[править]
Плоская ферма лежит в одной плоскости. [15] Плоские фермы обычно используются параллельно для формирования крыш и мостов. [17]
Глубина фермы, или высота между верхним и нижним поясами, делает ее эффективной структурной формой. Сплошная балка или балка равной прочности будут иметь значительный вес и стоимость материала по сравнению с фермой. Для заданного пролета более глубокая ферма потребует меньше материала на поясах и больше материала на вертикалях и диагоналях. Оптимальная глубина фермы максимизирует эффективность. [18]
Ферма с пространственной рамой[править]
Ферма с пространственной рамой представляет собой трехмерный каркас из элементов, закрепленных на концах. Форма тетраэдра — это простейшая пространственная ферма, состоящая из шести элементов, сходящихся в четырех суставах. [15] Большие плоские конструкции могут быть составлены из тетраэдров с общими ребрами, и они также используются в базовых конструкциях больших отдельно стоящих опор ЛЭП.
[15] Большие плоские конструкции могут быть составлены из тетраэдров с общими ребрами, и они также используются в базовых конструкциях больших отдельно стоящих опор ЛЭП.
- Дополнительные типы ферм см. в разделе Типы ферм, используемых в мостах.
Большая деревянная ферма Howe в коммерческом здании
Существует два основных типа ферм:
- Скатная ферма, или обычная ферма, характеризуется треугольной формой. Чаще всего используется для строительства крыш. Некоторые распространенные фермы названы в соответствии с их «сетевой конфигурацией». Размер пояса и конфигурация стенки определяются пролетом, нагрузкой и расстоянием.
- Ферма с параллельными поясами или плоская ферма получила свое название благодаря параллельным верхнему и нижнему поясам. Его часто используют для устройства пола.
Комбинация этих двух элементов представляет собой усеченную ферму, используемую в конструкции вальмовой крыши. Деревянная ферма, соединенная металлическими пластинами, представляет собой ферму крыши или пола, деревянные элементы которой соединены металлическими соединительными пластинами.
Деревянная ферма, соединенная металлическими пластинами, представляет собой ферму крыши или пола, деревянные элементы которой соединены металлическими соединительными пластинами.
Ферма Уоррена[править]
Основная статья: Ферма Уоррена
Элементы фермы образуют ряд равносторонних треугольников, чередующихся вверх и вниз.
Октетная ферма[править]
Элементы ферм состоят из всех эквивалентных равносторонних треугольников. Минимальная композиция — два правильных тетраэдра вместе с октаэдром. Они заполняют трехмерное пространство в различных конфигурациях.
Ферма Пратта
[20] В конструкции используются вертикальные элементы для сжатия и диагональные элементы для реагирования на растяжение. Конструкция ферм Пратта оставалась популярной, поскольку проектировщики мостов перешли с дерева на железо и с железа на сталь. [21] Эта постоянная популярность ферм Пратта, вероятно, связана с тем, что конфигурация элементов означает, что более длинные диагональные элементы растягиваются только из-за действия гравитационной нагрузки. Это позволяет использовать эти элементы более эффективно, поскольку эффекты гибкости, связанные с изгибом под действием сжимающих нагрузок (которые усугубляются длиной элемента), обычно не влияют на конструкцию. Следовательно, для данной плоской фермы с фиксированной глубиной конфигурация Пратта обычно является наиболее эффективной при статической вертикальной нагрузке.
Это позволяет использовать эти элементы более эффективно, поскольку эффекты гибкости, связанные с изгибом под действием сжимающих нагрузок (которые усугубляются длиной элемента), обычно не влияют на конструкцию. Следовательно, для данной плоской фермы с фиксированной глубиной конфигурация Пратта обычно является наиболее эффективной при статической вертикальной нагрузке.Железнодорожный мост Южно-Тихоокеанской железной дороги в Темпе, штат Аризона, представляет собой ферменный мост длиной 393 метра (1291 фут), построенный в 1912 году. Мост используется и по сей день.
Wright Flyer использовал ферму Пратта в конструкции крыла, так как минимизация длины сжимающих элементов позволила снизить аэродинамическое сопротивление. [24]
Тетивная ферма[править]
Тетивная ферма используется на самом старом металлическом мосту в Вирджинии
Названные в честь своей формы, тетивные фермы впервые использовались для арочных ферменных мостов, которые часто путали с мостами с арочными связями.
Тысячи тетивных ферм использовались во время Второй мировой войны для поддержки изогнутых крыш авиационных ангаров и других военных зданий. Существует множество вариантов расположения элементов, соединяющих узлы верхней дуги с узлами нижней прямой последовательности элементов, от почти равнобедренных треугольников до варианта фермы Пратта.
Ферма центральной стойки[править]
Основная статья: Центральная стойка
Один из самых простых в реализации стилей фермы, центральная стойка состоит из двух угловых опор, опирающихся на общую вертикальную опору.
Ферма шкворня, иногда шкворня или шкворня , похожа на ферму шкворня тем, что внешние опоры расположены под углом к центру конструкции. Основное отличие заключается в горизонтальном расширении в центре, которое зависит от действия балки для обеспечения механической устойчивости. Этот стиль ферм подходит только для относительно коротких пролетов. [25]
Лентикулярная ферма тип), имеют верхние и нижние пояса фермы арочные, образующие форму линзы.
 Мост с чечевицеобразными пони-фермами представляет собой конструкцию моста, в которой двояковыпуклая ферма проходит над и под дорожным полотном.
Мост с чечевицеобразными пони-фермами представляет собой конструкцию моста, в которой двояковыпуклая ферма проходит над и под дорожным полотном.Ферма решетчатая городская[править]
Основная статья: Мост с решетчатыми фермами
Американский архитектор Итиэль Таун разработал городскую решетчатую ферму как альтернативу мостам из тяжелого дерева. В его конструкции, запатентованной в 1820 и 1835 годах, используются удобные в обращении доски, расположенные по диагонали с короткими промежутками между ними, образующие решетку.
Ферма Виренделя[править]
См. также: Мост Артура Виренделя и Виренделя
Мост Виренделя, в основной конструкции которого отсутствуют диагональные элементы
Ферма Виренделя представляет собой конструкцию, в которой элементы не имеют треугольной формы, а образуют прямоугольные проемы, и представляет собой раму с неподвижными соединениями, способными передавать и сопротивляться изгибающим моментам. Таким образом, он не соответствует строгому определению фермы (поскольку он содержит элементы, не влияющие на две силы): обычные фермы включают элементы, которые, как обычно предполагается, имеют шарнирные соединения, что подразумевает отсутствие моментов на соединенных концах. Этот стиль строения был назван в честь бельгийского инженера Артура Виренделя, 9 лет.0269 [26] , который разработал конструкцию в 1896 году. Его использование для мостов редко из-за более высокой стоимости по сравнению с треугольной фермой.
Таким образом, он не соответствует строгому определению фермы (поскольку он содержит элементы, не влияющие на две силы): обычные фермы включают элементы, которые, как обычно предполагается, имеют шарнирные соединения, что подразумевает отсутствие моментов на соединенных концах. Этот стиль строения был назван в честь бельгийского инженера Артура Виренделя, 9 лет.0269 [26] , который разработал конструкцию в 1896 году. Его использование для мостов редко из-за более высокой стоимости по сравнению с треугольной фермой.
Полезность этого типа конструкции в зданиях заключается в том, что большая часть внешней оболочки остается свободной и может использоваться для оконных и дверных проемов. В некоторых приложениях это предпочтительнее, чем система с раскосной рамой, в которой некоторые области остаются закрытыми диагональными раскосами.
Статика[править]
Космонавт Александр Серебров устанавливает интегрированную ферменную конструкцию «Рапана» на ОК «Мир», 16, 19 сентября93
Ферма, которая, как предполагается, состоит из элементов, соединенных с помощью шарнирных соединений и поддерживаемых с обоих концов с помощью шарнирных соединений и роликов, считается статически определимой. Законы Ньютона применимы как к конструкции в целом, так и к каждому узлу или соединению. Для того чтобы любой узел, на который может действовать внешняя нагрузка или сила, оставался неподвижным в пространстве, должны выполняться следующие условия: суммы всех (горизонтальных и вертикальных) сил, а также всех моментов, действующих относительно узла, равны нулю. Анализ этих условий в каждом узле дает величину сил сжатия или растяжения.
Законы Ньютона применимы как к конструкции в целом, так и к каждому узлу или соединению. Для того чтобы любой узел, на который может действовать внешняя нагрузка или сила, оставался неподвижным в пространстве, должны выполняться следующие условия: суммы всех (горизонтальных и вертикальных) сил, а также всех моментов, действующих относительно узла, равны нулю. Анализ этих условий в каждом узле дает величину сил сжатия или растяжения.
Фермы, которые поддерживаются более чем в двух положениях, называются статически неопределимыми, и применения одних только законов Ньютона недостаточно для определения сил, действующих в стержнях.
Чтобы ферма с шарнирно соединенными элементами была устойчивой, она не обязательно должна состоять полностью из треугольников. [12] В математических терминах у нас есть следующее необходимое условие устойчивости простой фермы: а)} }
, где м — общее количество элементов фермы, j — общее количество соединений, а r — количество реакций (обычно равное 3) в двумерной конструкции.
Когда m = 2j−3{\displaystyle m=2j-3}, говорят, что ферма является статически определимой , потому что ( m +3 ) внутренние силы стержня и опорные реакции могут быть полностью определены формулой 2 j уравнений равновесия, если мы знаем внешние нагрузки и геометрию фермы. Учитывая определенное количество соединений, это минимальное количество элементов в том смысле, что если какой-либо элемент вынимается (или выходит из строя), то ферма в целом выходит из строя. Хотя соотношение (а) необходимо, его недостаточно для устойчивости, которая также зависит от геометрии фермы, условий поддержки и несущей способности элементов.
Некоторые конструкции имеют большее количество элементов фермы, чем это минимальное значение. Эти структуры могут выжить, даже если некоторые из членов терпят неудачу. Силы их стержней зависят от относительной жесткости стержней в дополнение к описанному условию равновесия.
Анализ[править]
Диаграмма Кремоны для плоской фермы
Поскольку силы в каждой из двух основных балок по существу плоские, ферма обычно моделируется как двумерная плоская рама. Однако при наличии значительных внеплоскостных сил конструкция должна быть смоделирована как трехмерное пространство.
Однако при наличии значительных внеплоскостных сил конструкция должна быть смоделирована как трехмерное пространство.
Расчет ферм часто предполагает, что нагрузки приложены только к соединениям, а не в промежуточных точках вдоль элементов. Вес элементов часто незначителен по сравнению с приложенными нагрузками, поэтому его часто не учитывают; в качестве альтернативы половина веса каждого элемента может приходиться на два его концевых соединения. При условии, что элементы длинные и тонкие, моменты, передаваемые через соединения, пренебрежимо малы, и соединения можно рассматривать как «шарниры» или «штифтовые соединения».
В соответствии с этими упрощающими предположениями каждый элемент фермы подвергается действию сил чистого сжатия или растяжения — сдвига, изгибающего момента и других более сложных нагрузок практически равны нулю. Фермы физически прочнее, чем другие способы расположения элементов конструкции, потому что почти каждый материал может выдерживать гораздо большую нагрузку при растяжении или сжатии, чем при сдвиге, изгибе, скручивании или других видах силы.
Эти упрощения облегчают анализ ферм. Структурный анализ ферм любого типа может быть легко выполнен с использованием матричного метода, такого как метод прямой жесткости, метод гибкости или метод конечных элементов.
Силы в стержнях Внешние нагрузки сосредоточены в наружных суставах. Поскольку это симметричная ферма с симметричными вертикальными нагрузками, реактивные силы в точках А и В равны друг другу и составляют половину общей нагрузки.
Внутренние силы в элементах фермы можно рассчитать различными способами, включая графические методы:
- Диаграмма Кремоны
- Диаграмма Кульмана
- Аналитический метод Риттера (метод сечений)
Расчет элементов[править]
Ферму можно рассматривать как балку, в которой стенка состоит из ряда отдельных элементов вместо сплошной пластины. В ферме нижний горизонтальный элемент (нижний пояс ) и верхний горизонтальный элемент (верхний пояс ) испытывают растяжение и сжатие, выполняя ту же функцию, что и полки двутавровой балки. Какая хорда несет растяжение, а какая сжатие, зависит от общего направления изгиба. В ферме, изображенной вверху справа, нижний пояс находится в напряжении, а верхний — в сжатии.
Какая хорда несет растяжение, а какая сжатие, зависит от общего направления изгиба. В ферме, изображенной вверху справа, нижний пояс находится в напряжении, а верхний — в сжатии.
Диагональные и вертикальные элементы образуют стенку фермы и воспринимают напряжение сдвига. По отдельности они также находятся на растяжение и сжатие, точное расположение сил зависит от типа фермы и опять же от направления изгиба. В ферме, показанной вверху справа, вертикальные элементы растянуты, а диагонали сжаты.
Секции фермы стабилизируют строящееся здание в Шанхае, в нем будут размещаться механические этажи
Помимо восприятия статических сил, элементы выполняют дополнительные функции стабилизации друг друга, предотвращая коробление. На соседнем рисунке верхний пояс защищен от коробления благодаря наличию распорок и жесткости перемычек.
Включение показанных элементов в значительной степени является инженерным решением, основанным на экономике, являющемся балансом между стоимостью сырья, изготовлением за пределами площадки, транспортировкой компонентов, монтажом на месте, наличием оборудования и стоимостью рабочей силы. В других случаях внешний вид конструкции может иметь большее значение и, таким образом, влиять на проектные решения, выходящие за рамки чисто экономических вопросов. Современные материалы, такие как предварительно напряженный бетон, и методы изготовления, такие как автоматическая сварка, значительно повлияли на конструкцию современных мостов.
В других случаях внешний вид конструкции может иметь большее значение и, таким образом, влиять на проектные решения, выходящие за рамки чисто экономических вопросов. Современные материалы, такие как предварительно напряженный бетон, и методы изготовления, такие как автоматическая сварка, значительно повлияли на конструкцию современных мостов.
Когда сила, действующая на каждый элемент, известна, следующим шагом является определение поперечного сечения отдельных элементов фермы. Для растянутых элементов площадь поперечного сечения A можно найти, используя A = F × γ / σ y , где F — сила в элементе, γ — коэффициент безопасности ( обычно 1,5, но в зависимости от строительных норм и правил), а σ y — предел текучести используемой стали при растяжении.
Элементы, находящиеся под сжатием, также должны быть спроектированы таким образом, чтобы они были защищены от коробления.
Вес элемента фермы напрямую зависит от его поперечного сечения — этот вес частично определяет, насколько прочными должны быть другие элементы фермы. Придание одному стержню большего поперечного сечения, чем в предыдущей итерации, требует, чтобы другие стержни также имели большее поперечное сечение, чтобы удерживать больший вес первого стержня — нужно пройти еще одну итерацию, чтобы точно определить, насколько больше требуется другим стержням. быть. Иногда проектировщик выполняет несколько итераций процесса проектирования, чтобы прийти к «правильному» поперечному сечению для каждого элемента. С другой стороны, уменьшение размера одного элемента по сравнению с предыдущей итерацией просто приводит к тому, что другие элементы имеют больший (и более дорогой) запас прочности, чем это необходимо с технической точки зрения, но не 9.0582 требуется еще одна итерация, чтобы найти сборную ферму.
Придание одному стержню большего поперечного сечения, чем в предыдущей итерации, требует, чтобы другие стержни также имели большее поперечное сечение, чтобы удерживать больший вес первого стержня — нужно пройти еще одну итерацию, чтобы точно определить, насколько больше требуется другим стержням. быть. Иногда проектировщик выполняет несколько итераций процесса проектирования, чтобы прийти к «правильному» поперечному сечению для каждого элемента. С другой стороны, уменьшение размера одного элемента по сравнению с предыдущей итерацией просто приводит к тому, что другие элементы имеют больший (и более дорогой) запас прочности, чем это необходимо с технической точки зрения, но не 9.0582 требуется еще одна итерация, чтобы найти сборную ферму.
Влияние веса отдельных элементов фермы в большой ферме, такой как мост, обычно незначительно по сравнению с силой внешних нагрузок.
Проект соединений . В зависимости от требований проекта внутренние соединения (узлы) фермы могут быть выполнены жесткими, полужесткими или шарнирными.
 Жесткие соединения могут допускать передачу изгибающих моментов, что приводит к возникновению вторичных изгибающих моментов в элементах.
Жесткие соединения могут допускать передачу изгибающих моментов, что приводит к возникновению вторичных изгибающих моментов в элементах.Применение[править]
Тип фермы, используемой в кровле
Каркасные конструкции[править]
Соединения компонентов имеют решающее значение для структурной целостности каркасной системы. В зданиях с деревянными фермами с большим пролетом наиболее важными являются соединения между фермой и ее опорами. В дополнение к силам, вызванным гравитацией (также известным как нагрузки на подшипники), эти соединения должны противостоять силам сдвига, действующим перпендикулярно плоскости фермы, и силам подъема, вызванным ветром. В зависимости от общей конструкции здания соединения могут также потребоваться для передачи изгибающего момента.
Деревянные стойки позволяют создавать прочные, прямые и недорогие соединения между большими фермами и стенами. Точные детали соединений столбов с фермами варьируются от проектировщика к проектировщику и могут зависеть от типа столба. Массивные пиломатериалы и столбы из клееного бруса обычно имеют надрезы для образования несущей поверхности фермы. Ферма упирается в пазы и крепится болтами. Можно добавить специальную пластину/кронштейн для увеличения возможности передачи нагрузки соединения. С механически ламинированными стойками ферма может опираться на укороченный внешний слой или на укороченный внутренний слой. В более позднем сценарии болты подвергаются двойному сдвигу, что является очень эффективным соединением.
Массивные пиломатериалы и столбы из клееного бруса обычно имеют надрезы для образования несущей поверхности фермы. Ферма упирается в пазы и крепится болтами. Можно добавить специальную пластину/кронштейн для увеличения возможности передачи нагрузки соединения. С механически ламинированными стойками ферма может опираться на укороченный внешний слой или на укороченный внутренний слой. В более позднем сценарии болты подвергаются двойному сдвигу, что является очень эффективным соединением.
Галерея Мост
Мост Окленд-Харбор, вид с острова Уотчмен на запад
Мост Литтл-Белт : мост с фермами в Дании
Сборные стальные тетивные фермы крыши, построенные в 1942 году для объектов военного ведомства в Северной Австралии
Ферма крыши бокового здания аббатства Клюни, Франция
Разрез через деревянную ферму крыши
Космическая ферма, несущая пол в The Woodlands Mall
Опора электропередач
Деревянная ферма крыши
Современный временный мост из панелей фермы моста Бейли в Монреале, Квебек
Трехмерная конструкция фермы
Пример расчета усилий фермы, выполненный программой, использующей матричный метод решения Гаусса
92 См.
 также[править]
также[править]- Решетчатая башня
- Мозаика Андреини, единственные 28 способов заполнить трехмерное пространство фермами, которые имеют одинаковых соединения повсюду
- Коричневая ферма
- Geodesic Dome, ферма в форме сферы
- Структурная механика
- Serririer Frus
- Ферма из тенсегрити, ферма, в которой ни один сжимаемый элемент не касается другого сжимаемого элемента
- Анкерный стержень, часть гитары
Каталожные номера[править]
- 9 Vierendeel bruggen
Внешние ссылки
Из: Structural and Stress Analysis (Fourth Edition), 2019
PlusAdd to Mendeley Dr.T.H.G. Мегсон, в Structural and Stress Analysis (четвертое издание), 2019
16.1 Методы определения гибкости и жесткости
В разделе 4.4 мы кратко обсудили статическую неопределенность ферм и установили не всегда применимое условие устойчивости и статически определимой фермы. В этом условии, связанном с числом членов и числом соединений, не было опорных реакций, которые сами по себе могли быть как статически определенными, так и неопределенными. Таким образом, условие было одним из внутренней статической определенности; ясно, что детерминированность, или иначе, опорных реакций является одной из внешней статической детерминированности.
В этом условии, связанном с числом членов и числом соединений, не было опорных реакций, которые сами по себе могли быть как статически определенными, так и неопределенными. Таким образом, условие было одним из внутренней статической определенности; ясно, что детерминированность, или иначе, опорных реакций является одной из внешней статической детерминированности.
Рассмотрим портальную раму, показанную на рис. 16.1. Рама несет нагрузки, P и W , в своей плоскости, так что система является двухмерной. Поскольку вертикальные элементы AB и FD рамы закреплены в точках A и F, приложенные нагрузки будут генерировать в общей сложности шесть реакций силы и момента, как показано на рисунке. Для двумерной системы возможны три уравнения статического равновесия (уравнение (2.10)), так что репер внешне статически неопределим до третья степень. Ситуация не улучшается при разрезании одного из элементов, поскольку эта процедура, хотя и устраняет один из наборов реактивных сил, вводит три равнодействующие внутренних напряжений. Если бы, однако, были известны три опорные реакции или, наоборот, если бы были известны три равнодействующие внутренних напряжений, то оставшиеся три неизвестных можно было бы определить из уравнений статического равновесия, и решение было завершено.
Если бы, однако, были известны три опорные реакции или, наоборот, если бы были известны три равнодействующие внутренних напряжений, то оставшиеся три неизвестных можно было бы определить из уравнений статического равновесия, и решение было завершено.
Рисунок 16.1. Статическая неопределенность портальной рамы.
Другая ситуация возникает в простой ферме, показанной на рис. 4.7(б), где, как мы видели, дополнительная диагональ приводит к тому, что ферма становится внутренне статически неопределимой до первой степени; обратите внимание, что опорные реакции статически определимы.
При анализе статически неопределимых конструкций используются два основных метода. В одном случае конструкция приводится к статически определяемому состоянию за счет использования расцепителей , т. е. путем исключения достаточного количества неизвестных, позволяющих найти опорные реакции и/или результирующие внутренние напряжения из рассмотрения статического равновесия. Например, в раме на рис. 16.1 число опорных реакций сократилось бы до трех, если бы одна из опор была шарнирной, а другая — роликовой. Тот же результат был бы достигнут, если бы одна опора оставалась неподвижной, а другая полностью удалялась. Кроме того, в ферме на рис. 4.7(b) удаление диагонального, вертикального или горизонтального элемента приведет к тому, что ферма станет статически определимой. Освобождение конструкции таким образом приведет к смещениям, которых в противном случае не было бы. Эти смещения могут быть рассчитаны путем анализа выпущенной статически определимой конструкции; тогда получается система сил, необходимая для их устранения, т. е. мы используем условие совместимости перемещений. Этот метод обычно называют гибкость или метод силы ; в действительности этот метод был использован при решении подпираемой консоли на рис. 13.25.
Например, в раме на рис. 16.1 число опорных реакций сократилось бы до трех, если бы одна из опор была шарнирной, а другая — роликовой. Тот же результат был бы достигнут, если бы одна опора оставалась неподвижной, а другая полностью удалялась. Кроме того, в ферме на рис. 4.7(b) удаление диагонального, вертикального или горизонтального элемента приведет к тому, что ферма станет статически определимой. Освобождение конструкции таким образом приведет к смещениям, которых в противном случае не было бы. Эти смещения могут быть рассчитаны путем анализа выпущенной статически определимой конструкции; тогда получается система сил, необходимая для их устранения, т. е. мы используем условие совместимости перемещений. Этот метод обычно называют гибкость или метод силы ; в действительности этот метод был использован при решении подпираемой консоли на рис. 13.25.
Альтернативная процедура, известная как метод жесткости или метод смещения , аналогична методу гибкости, главное отличие состоит в том, что неизвестными являются смещения в определенных точках конструкции. Как правило, процедура требует, чтобы конструкция была разделена на ряд элементов, для каждого из которых известны отношения нагрузка-перемещение. Затем уравнения равновесия записываются в терминах перемещений в местах соединения элементов и решаются для требуемых перемещений; следует полное решение.
Как правило, процедура требует, чтобы конструкция была разделена на ряд элементов, для каждого из которых известны отношения нагрузка-перемещение. Затем уравнения равновесия записываются в терминах перемещений в местах соединения элементов и решаются для требуемых перемещений; следует полное решение.
Как методы гибкости, так и методы определения жесткости обычно приводят для практических конструкций, имеющих высокую степень статической неопределенности, к большому количеству одновременных уравнений, которые легче всего решить с помощью компьютерных методов. Однако метод гибкости требует, чтобы структура была приведена к статически определенному состоянию путем вставки выпусков, процедура, требующая некоторого суждения со стороны аналитика. С другой стороны, метод жесткости не требует такой оценки и поэтому особенно подходит для автоматических вычислений.
Хотя практическое применение методов гибкости и жесткости, как правило, основано на компьютере, они являются фундаментальными для «ручных» методов анализа, как мы увидим далее. Прежде чем исследовать эти ручные методы, мы более подробно рассмотрим неопределенность структур, поскольку нам потребуется степень неопределенности конструкции, прежде чем в случае гибкого метода можно будет определить соответствующее количество релизов. В то же время кинематическая неопределенность конструкции, необходимо определить количество ограничений, которые необходимо применить, чтобы сделать конструкцию кинематически определимой в методе жесткости.
Прежде чем исследовать эти ручные методы, мы более подробно рассмотрим неопределенность структур, поскольку нам потребуется степень неопределенности конструкции, прежде чем в случае гибкого метода можно будет определить соответствующее количество релизов. В то же время кинематическая неопределенность конструкции, необходимо определить количество ограничений, которые необходимо применить, чтобы сделать конструкцию кинематически определимой в методе жесткости.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B9780081025864000160
М. Билл Вонг, Анализ пластмасс и проектирование стальных конструкций,209
Сводка издателя
В этой главе представлены общие методы анализа пластичности, в которых используются современные вычислительные средства, такие как программы линейного упругого анализа и приложения для работы с электронными таблицами. Мощные возможности этих инструментов для обработки чисел позволяют выполнять анализ и проектирование конструкций практически любого размера. Объем вычислений, необходимых для структурного анализа, в значительной степени зависит от степени статической неопределенности конструкции. Структурный анализ, будь то линейный или нелинейный, в основном основан на матричных формулировках для обработки огромного количества числовых данных и вычислений. Матричные формулировки подходят для компьютерной реализации и могут быть применены к двум основным методам структурного анализа: методу гибкости (или силы) и методу жесткости (или смещения). В этой главе основное внимание уделяется методу жесткости. Формулировка матричных уравнений для метода жесткости выполняется рутинно, а процедура решения носит систематический характер. Поэтому метод жесткости используется в большинстве компьютерных программ расчета конструкций. Этот метод особенно полезен для конструкций с высокой степенью статической неопределенности, хотя его можно использовать как для определенных, так и для неопределенных конструкций.
Мощные возможности этих инструментов для обработки чисел позволяют выполнять анализ и проектирование конструкций практически любого размера. Объем вычислений, необходимых для структурного анализа, в значительной степени зависит от степени статической неопределенности конструкции. Структурный анализ, будь то линейный или нелинейный, в основном основан на матричных формулировках для обработки огромного количества числовых данных и вычислений. Матричные формулировки подходят для компьютерной реализации и могут быть применены к двум основным методам структурного анализа: методу гибкости (или силы) и методу жесткости (или смещения). В этой главе основное внимание уделяется методу жесткости. Формулировка матричных уравнений для метода жесткости выполняется рутинно, а процедура решения носит систематический характер. Поэтому метод жесткости используется в большинстве компьютерных программ расчета конструкций. Этот метод особенно полезен для конструкций с высокой степенью статической неопределенности, хотя его можно использовать как для определенных, так и для неопределенных конструкций. Кроме того, метод жесткости используется в упругопластическом анализе, описанном в этой главе. В заключение утверждается, что в структурном анализе важна степень статической неопределенности, поскольку ее значение может определять, является ли конструкция глобально нестабильной или стабильной.
Кроме того, метод жесткости используется в упругопластическом анализе, описанном в этой главе. В заключение утверждается, что в структурном анализе важна степень статической неопределенности, поскольку ее значение может определять, является ли конструкция глобально нестабильной или стабильной.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B9780750682985000016
Dr.T.H.G. Megson, Structural and Stress Analysis (Fourth Edition), 2019
1.7 Идеализация конструкции и нагрузки
Как правило, конструкции являются сложными и должны быть идеализированы или упрощены до формы, которую можно проанализировать. Эта идеализация зависит от таких факторов, как степень точности, требуемой от анализа, поскольку, как правило, чем сложнее используемый метод анализа, тем больше времени и, следовательно, он дороже. Предварительная оценка двух или более возможных проектных решений не требует такой степени точности, как проверка окончательного проекта. Другие факторы, влияющие на идеализацию, включают тип применяемой нагрузки, поскольку возможно, что конструкция потребует различных идеализаций при разных нагрузках.
Предварительная оценка двух или более возможных проектных решений не требует такой степени точности, как проверка окончательного проекта. Другие факторы, влияющие на идеализацию, включают тип применяемой нагрузки, поскольку возможно, что конструкция потребует различных идеализаций при разных нагрузках.
В разделе 1.4 мы видели, как идеализируются реальные опоры. Пример структурной идеализации показан на рис. 1.19, где простая ферма крыши на рис. 1.19 (а) опирается на колонны и образует одну из серии, включающей конструкцию крыши. Облицовка крыши крепится к ферме через прогоны, соединяющие каждую ферму, а элементы фермы соединяются друг с другом косынками, которые могут быть приклепаны или приварены к элементам, образуя жесткие соединения. Эта структура обладает высокой степенью статической неопределенности, и ее анализ, вероятно, потребует компьютерного подхода. Однако допущение о простой опорной системе, замена жестких соединений шарнирными или шарнирными соединениями и допущение, что силы в элементах являются чисто осевыми, приводят, как мы увидим в главе 4, к статически определимой конструкции ( Рис. 1.19(б)). Такая идеализация может показаться чрезмерной, но пока нагрузки приложены к стыкам и ферма опирается на стыки, силы в элементах являются преимущественно осевыми, а изгибающие моменты и поперечные силы пренебрежимо малы.
1.19(б)). Такая идеализация может показаться чрезмерной, но пока нагрузки приложены к стыкам и ферма опирается на стыки, силы в элементах являются преимущественно осевыми, а изгибающие моменты и поперечные силы пренебрежимо малы.
Рисунок 1.19. (а) Реальная ферма и (б) идеализированная ферма.
С другой стороны, континуальная структура, такая как фальцевая плоская крыша, может быть идеализирована в большое количество конечных элементов , соединенных в узлах и проанализированных с помощью компьютера; 9Метод конечных элементов 3160 фактически является исключительно компьютерной техникой. В пакетах конечных элементов доступен широкий диапазон элементов, включая простые балочные элементы, пластинчатые элементы, которые могут моделировать как плоскостные, так и внеплоскостные эффекты, а также трехмерные «кирпичные» элементы для идеализации твердых трехмерных объектов. структуры.
Помимо идеализации конструкции, как правило, также необходимо идеализировать нагрузки. На рис. 1.20 (а) балка AB поддерживает две поперечные балки, на которых стоит контейнер. Конечно, должна быть вторая балка, параллельная AB, для поддержки другого конца каждой поперечной балки. Фланец каждой поперечной балки применяет распределенная нагрузка на балку AB, но если ширина полки мала по отношению к пролету балки, их можно рассматривать как сосредоточенные нагрузки , как показано на рис. 1.20 (б). На практике такой вещи, как сосредоточенная нагрузка, не существует, поскольку, помимо практических трудностей ее применения, нагрузка, действующая на нулевую площадь, означает, что напряжение (см. главу 7) будет бесконечным и произойдет локальный отказ.
На рис. 1.20 (а) балка AB поддерживает две поперечные балки, на которых стоит контейнер. Конечно, должна быть вторая балка, параллельная AB, для поддержки другого конца каждой поперечной балки. Фланец каждой поперечной балки применяет распределенная нагрузка на балку AB, но если ширина полки мала по отношению к пролету балки, их можно рассматривать как сосредоточенные нагрузки , как показано на рис. 1.20 (б). На практике такой вещи, как сосредоточенная нагрузка, не существует, поскольку, помимо практических трудностей ее применения, нагрузка, действующая на нулевую площадь, означает, что напряжение (см. главу 7) будет бесконечным и произойдет локальный отказ.
Рисунок 1.20. Идеализация системы нагрузки.
Нагрузка, воспринимаемая поперечными балками, т. е. контейнером, вероятно, будет приложена на значительной части их длины, как показано на рис. 1.21(а). В этом случае говорят, что нагрузка равна равномерно распределены по длине CD поперечной балки и представлены, как показано на рис. 1.21 (б).
1.21 (б).
Рисунок 1.21. Идеализация системы нагрузки: равномерно распределенная.
Распределенные нагрузки не обязательно должны быть равномерными, но могут быть трапециевидными или, в более сложных случаях, описываться математической функцией. Отметим, что все балки на рис. 1.20 и 1.21 несут равномерно распределенную нагрузку, собственный вес.
Просмотр главыКнига покупок
Read full chapter
URL: https://www.sciencedirect.com/science/article/pii/B9780081025864000019
László P. Kollár, Gabriella Tarján, in Mechanics of Civil Engineering Structures, 2021
9.2 .4 Роль пластичности в сейсмостойком расчете
Теперь расчет пластичности применяется к горизонтально нагруженным рамам (рис. 9.18). Несущая способность поперечных сечений указана ( M y ) и может быть разной для разных сечений. При небольших горизонтальных нагрузках конструкция ведет себя упруго; то при определенной нагрузке на одном из сечений появляется пластический шарнир. В дальнейшем примем здесь шарнир, но применяя равномерную пару моментов ( М и ). Для более высоких нагрузок появляются новые пластиковые шарниры, которые обрабатываются аналогично, и, наконец, конструкция становится механизмом, и мы достигаем несущей способности конструкции. В этой точке (без учета эффектов второго порядка) кривая нагрузки-перемещения горизонтальна, и конструкция не имеет жесткости. Если степень статической неопределенности n , то количество пластических шарниров равно или меньше n + 1. f
В дальнейшем примем здесь шарнир, но применяя равномерную пару моментов ( М и ). Для более высоких нагрузок появляются новые пластиковые шарниры, которые обрабатываются аналогично, и, наконец, конструкция становится механизмом, и мы достигаем несущей способности конструкции. В этой точке (без учета эффектов второго порядка) кривая нагрузки-перемещения горизонтальна, и конструкция не имеет жесткости. Если степень статической неопределенности n , то количество пластических шарниров равно или меньше n + 1. f
Рис. 9.18. Рама, подверженная горизонтальным нагрузкам, выработки пластичных шарниров. На нижнем рисунке показана диаграмма нагрузки-перемещения.
Если сооружение подвергается землетрясениям, применение приведенного выше анализа дает дополнительное преимущество: сейсмическая нагрузка может быть значительно снижена. Это наблюдали Велетсос и Ньюмарк, и они представили это как «правило равных перемещений», согласно которому максимальные смещения упругопластических конструкций зависят — в разумном приближении — только от (начальной, упругой) жесткости конструкции и не зависит от сопротивления нагрузки. г Это показано на рис. 9.19: показаны кривые силы-перемещения трех конструкций с одинаковой начальной (упругой) жесткостью, но с разным сопротивлением нагрузке. При землетрясении они испытывают примерно одинаковое максимальное смещение ( u м ), хотя первое упругое, а два других упруго-пластические. Как следствие, если, например, сейсмостойкость составляет только одну пятую нагрузки, рассчитанной на абсолютно упругую конструкцию, конструкция может выдержать землетрясение при условии, что она имеет достаточную пластичность. (В этом примере, согласно «правилу равных перемещений», его полное перемещение будет в пять раз больше перемещения, принадлежащего пределу упругости. Требование пластичности, т. е. отношение требуемого полного перемещения к упругому перемещению, пять.)
г Это показано на рис. 9.19: показаны кривые силы-перемещения трех конструкций с одинаковой начальной (упругой) жесткостью, но с разным сопротивлением нагрузке. При землетрясении они испытывают примерно одинаковое максимальное смещение ( u м ), хотя первое упругое, а два других упруго-пластические. Как следствие, если, например, сейсмостойкость составляет только одну пятую нагрузки, рассчитанной на абсолютно упругую конструкцию, конструкция может выдержать землетрясение при условии, что она имеет достаточную пластичность. (В этом примере, согласно «правилу равных перемещений», его полное перемещение будет в пять раз больше перемещения, принадлежащего пределу упругости. Требование пластичности, т. е. отношение требуемого полного перемещения к упругому перемещению, пять.)
Рис. 9.19. Кривые силы-перемещения трех конструкций с одинаковой начальной (упругой) жесткостью для иллюстрации правила равных перемещений: при землетрясении они испытывают примерно одинаковое максимальное перемещение ( u м ), хотя первое является упругим , а два других упругопластические.
Теперь мы можем ввести простую процедуру проектирования для анализа пластичных конструкций. Эластичная сейсмостойкая конструкция обычно основана на спектре упругой реакции S e ( T ) (см. рис. 8.28), который приведен в стандартах, а теоретическая кривая показана вверху рис. 9.20. Нагрузка от землетрясения пропорциональна S e . Из-за пластичности можно сделать уменьшение, и таким образом мы получим расчетный спектр отклика S d . Коэффициент снижения отклика обозначается R (в Еврокоде 8 это коэффициент поведения и обозначается β [7]), а также приводится в стандартах; одна кривая показана на рис. 9.21 [4]. Обратите внимание, что правило равных перемещений выполняется только для относительно гибких конструкций ( T > T C ), где R равно пластичности ( R = μ ). Для очень жестких конструкций R = 1.
Рис. 9.20. Кривая упругого и расчетного спектра отклика с учетом коэффициента снижения отклика ( R ) из-за пластичности [25].
9.20. Кривая упругого и расчетного спектра отклика с учетом коэффициента снижения отклика ( R ) из-за пластичности [25].
Рис. 9.21. Коэффициент снижения отклика ( R ) для различных значений пластичности (мк) в зависимости от периода колебаний конструкции (логарифмическая шкала) [4]. T A , T B и T C — характерные точки спектра отклика (см. рис. 9.20).
Кривые силы-перемещения реальных конструкций нелинейны, что может быть аппроксимировано билинейными кривыми, как показано на рис. 9.22. При этом общая пластичность конструкции: мкм = d m / d y можно определить.
Рис. 9.22. Кривая сила-перемещение рамы. Расчет пластичности ( μ = d m / d y ) по «идеальной» упругопластической кривой.
Хотя этот расчет полезен, его можно выполнить только при наличии достаточной пластичности пластиковых шарниров. Следует также отметить, что при пластическом расчете смещения велики, и межэтажные сдвиги могут привести к повреждению связанных конструкций. Кроме того, пластические деформации усиливают эффекты второго порядка.
Следует также отметить, что при пластическом расчете смещения велики, и межэтажные сдвиги могут привести к повреждению связанных конструкций. Кроме того, пластические деформации усиливают эффекты второго порядка.
Индекс упругой устойчивости θ E определяется формулой. (7.170) должно быть изменено из-за пластических деформаций, и, таким образом, мы имеем показатель пластической устойчивости (или просто показатель устойчивости) как: F — сумма горизонтальных сил, а d p — соответствующий «межэтажный сдвиг», включающий как упругие, так и пластические деформации, составляющий около R раз (в ЭК β раз) упругий дрейф. Это выражение приведено в EC8 [7], а утверждения на стр. 245 изменены: если индекс (пластической) устойчивости меньше 0,1 ( θ < 0,1), то эффектами второго порядка можно пренебречь, а если θ > 0,3, горизонтальная связь должна быть усилена, и при расчете коэффициента увеличения смещения (уравнения 7. 35, 7.83) необходимо использовать θ вместо θ E . Обратите внимание, что для требований высокой пластичности θ также может быть высоким: θ / θ E ≈ μ .
35, 7.83) необходимо использовать θ вместо θ E . Обратите внимание, что для требований высокой пластичности θ также может быть высоким: θ / θ E ≈ μ .
Понижающий коэффициент R может быть довольно высоким, даже выше 8. Для высокой пластичности расчет более сложный, чем простое снижение нагрузок; это называется «проектирование емкости».
Расчет емкости
Одним из первых разработчиков конструкции емкости [26] является Томас Паулай (1923–2009), покинувший Венгрию в 1948 г., живший и работавший в Новой Зеландии. Как он сам заявил, при проектировании мощностей мы «говорим структуре, как себя вести».
Конструкция должна быть спроектирована таким образом, чтобы в пластических шарнирах развивались пластические деформации, а остальная часть конструкции оставалась упругой. Обычный инженерный проект обычно не заботится о завышении поперечных сечений; однако для пластиковых шарниров это может быть очень опасно, поскольку более высокий момент текучести в пластиковом шарнире означает более высокие сейсмические нагрузки, которые могут вызвать хрупкое разрушение элемента за пределами пластикового шарнира. Следовательно, основные этапы проектирования мощностей следующие [26]:
Следовательно, основные этапы проектирования мощностей следующие [26]:
- •
Внутренние силы, вызванные землетрясением, определяются с учетом уменьшения (рис. 9.20) за счет общей пластичности конструкции.
- •
Определяем расположение пластиковых петель, в результате получается механизм. Детализация зон пластичных шарниров очень важна и подробно рассмотрена, например, в Еврокоде [7].
- •
Те части конструкции, которые находятся за пределами пластиковых шарниров, рассчитаны на более высокие внутренние силы, чем полученные в результате анализа:
(9.7)EEd=γγovΩEEd,E,
где
- •
E Ed, E — внутренняя сила, полученная из анализа.
- •
Ом – отношение расчетного сопротивления к требуемому сопротивлению пластиковых петель.
- •
γ ov – «коэффициент сверхпрочности» материала пластиковых шарниров (отношение реального предела текучести к расчетному пределу текучести).

- •
γ — коэффициент безопасности.
Этот расчет гарантирует, что пластмассовые петли прогибаются раньше, чем другие части конструкции.
Значение рисунка пластикового механизма показано на рис. 9.23. Предположим, что возможная пластическая деформация пластического шарнира равна Θ y , и определите соответствующее пластическое смещение вершины. На рис. 9.23а при наличии пластических шарниров на концах балок возможное смещение вершины равно D = θ Y H , в то время как на рис. 9.23B, где есть пластиковые шарниры на концах столбцов первого этажа D = θ 16042041661616161616161616161616 гг. . Для достижения такого же верхнего прогиба пятиэтажного каркаса местная пластичность во втором случае должна быть в пять раз больше. Этот случай называется механизмом «мягкой истории», и его следует избегать.
Рис. 9.23. Сравнение двух возможных пластиковых механизмов рамы. Второй случай — это механизм «мягкой истории», которого следует избегать.
Второй случай — это механизм «мягкой истории», которого следует избегать.
Посмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B9780128203217000095
Блок для изучения деформации ферм
Лаборатории
Общее описание
Установка для изучения деформирования ферм «MFCS3» позволяет измерять напряжения в стержнях в различных типах ферм, а также изучать зависимость внешней силы и сравнивать экспериментальные усилия в стержнях с математическими методы, подобные методу сечений, теореме Риттера или Кастильяно.
Блок состоит из двадцати одного стержня из ПВХ (для точного наблюдения за деформациями) разной длины для формирования различных ферменных конструкций.
Стержни будут работать на растяжение или сжатие и будут размещены в виде треугольных блоков под разными углами. Стержни можно считать идеальными, так как пренебрегается трением и узлы не передают моментов.
Для создания внешней силы к узловому диску присоединяется устройство приложения нагрузки. Это устройство включает датчик силы, который может быть установлен на различных узловых дисках, траверсу для поперечной устойчивости фермы и циферблатный индикатор для регистрации деформации фермы под нагрузкой.
Каркас включает в себя три опоры, две из них для создания опор в двух узловых дисках конструкции и еще одну для размещения ребер жесткости для предотвращения коробления конструкции.
Теорема Кастильяно может быть доказана для расчета деформации энергетическими методами.
Упражнения и практические рекомендации
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ С РУКОВОДСТВОМ, ВКЛЮЧЕННЫЕ В РУКОВОДСТВО
- Исследование упругой деформации фермы под действием точечной нагрузки.
- Расчет опорной реакции и сил стержня.
- Изучение принципа работы и энергии деформации.
- Расчет деформации в заданной точке с применением первой теоремы Кастильяно.

- Сравнение деформаций различных ферм при одинаковой нагрузке.
- Сравнение экспериментальной деформации с расчетной.
ПОДОБНЫХ УСТРОЙСТВ
- MFCS1
В наличии
7.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MFCS1
Блок изучения усилий в различных одноплоскостных фермах
Устройство для изучения усилий в различных одноплоскостных фермах «MFCS1» позволяет измерять усилия на стержнях в различных одноплоскостных фермах, изучать зависимость от внешней силы и сравнивать экспериментальные усилия на стержнях…
- MFCS2
В наличии
7.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MFCS2
Блок изучения сил в сверхопределенной ферме
Блок для изучения сил в переопределенной ферме «MFCS2» позволяет измерять усилия на стержнях в статически неопределимой ферме и в статически переопределенной ферме, изучать распределение усилий в одной плоскости…
- МФБС
В наличии
7. 1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MFBS
Блок изучения усилий в простой стержневой конструкции
Устройство для изучения сил в простой стержневой конструкции «MFBS», разработанное EDIBON, позволяет изучать силы, действующие на простую ферму, когда она подвергается точечной нагрузке в одном из узлов, составляющих конструкцию. Он состоит группы из пяти…
ДОПОЛНИТЕЛЬНОЕ ОБОРУДОВАНИЕ
- МФПГ
В наличии
14.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MFPG
Модуль для изучения сил в стреловом кране
Установка для изучения сил в стреловом кране «МФПГ» предназначена для исследования растягивающих и сжимающих усилий в плоской системе центральных сил на примере стрелы крана. Блок представляет собой плоскую центральную силовую систему, в которой…
- МВС
В наличии
14.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
МВС
Висячий мост
Блок висячего моста MVS состоит из настила и двух параллельных основных тросов, которые имитируют висячий мост и позволяют исследовать нагрузку на основные тросы. Настил моста имитируется балкой из легкого сплава, удерживаемой обеими…
Настил моста имитируется балкой из легкого сплава, удерживаемой обеими…
- КАРТА
В наличии
14.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
КАРТА
Параболическая арка
Блок параболической арки «MARP» содержит предварительно сформированную шарнирную арку, которая может подвергаться точечной или равномерно распределенной нагрузке с помощью семи равномерно распределенных тросов (тросов) с подвесками. ..
- МАРТ
В наличии
14.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
МАРТ
Трехшарнирная арка
Трехшарнирная арочная установка «МАРТ» позволяет студенту ознакомиться с трехшарнирными арками, рассчитать опорные усилия (при точечной нагрузке, при равномерно распределенной нагрузке и при подвижной нагрузке), исследовать влияние нагрузки на…
- МФБС
В наличии
7.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MFBS
Блок изучения усилий в простой стержневой конструкции
Устройство для изучения сил в простой стержневой конструкции «MFBS», разработанное EDIBON, позволяет изучать силы, действующие на простую ферму, когда она подвергается точечной нагрузке в одном из узлов, составляющих конструкцию. Он состоит группы из пяти…
Он состоит группы из пяти…
- MFCS1
Доступно
7.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MFCS1
Блок изучения усилий в различных одноплоскостных фермах
Устройство для изучения усилий в различных одноплоскостных фермах «MFCS1» позволяет измерять усилия на стержнях в различных одноплоскостных фермах, изучать зависимость от внешней силы и сравнивать экспериментальные усилия на стержнях…
- MFCS2
В наличии
7.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MFCS2
Блок изучения сил в сверхопределенной ферме
Блок для изучения сил в переопределенной ферме «MFCS2» позволяет измерять усилия на стержнях в статически неопределимой ферме и в статически переопределенной ферме, изучать распределение усилий в одной плоскости…
- MCPG
В наличии
7.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MCPG
Толстостенный цилиндр
В блоке толстостенных цилиндров «MCPG» напряжения определяются путем измерения деформаций, возникающих на поверхности. Эти деформации измеряются тензодатчиками. Толстостенный сосуд состоит из алюминиевого цилиндра длиной…
Эти деформации измеряются тензодатчиками. Толстостенный сосуд состоит из алюминиевого цилиндра длиной…
- МФЛ
В наличии
14.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MFL
Двухшарнирная арка
Двухшарнирный арочный блок «MFL», разработанный EDIBON, позволяет исследовать реакцию арочной балки на воздействие внешней нагрузки. Арка опирается на две опоры, неподвижную и подвижную. Водоизмещение и горизонталь…
- МПО
В наличии
7.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
MPO
Блок каркаса портала
Блок портальной рамы «MPO» позволяет выполнять измерения вертикального и горизонтального отклонения в фиксированных прямоугольных портальных рамах.
- СТХ
В наличии
7.1.6.- СТРОИТЕЛЬНАЯ МЕХАНИКА
ТУ
Группа стрессовых гипотез
Блок гипотез о напряжении, «STH», позволяет изучать и проверять гипотезы о напряжении путем приложения нагрузок в разных направлениях к точке испытательного образца и измерения возникающих деформаций.



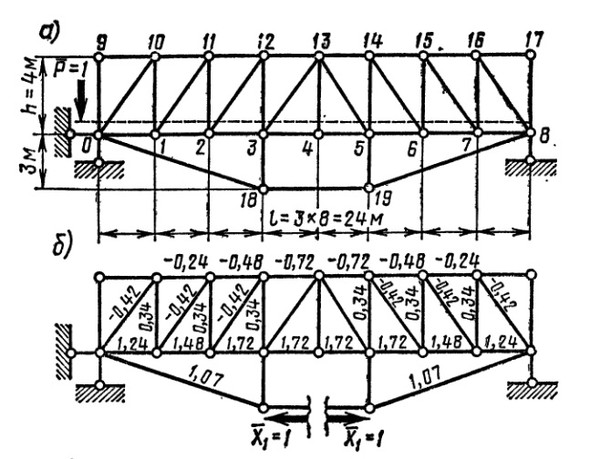 Размещаем помещаем элементы на свободное поле кликом левой кнопки мыши. Чтобы указать точные координаты опор, переходим в режим редактирования, нажав на значок курсора на панели инструментов.
Размещаем помещаем элементы на свободное поле кликом левой кнопки мыши. Чтобы указать точные координаты опор, переходим в режим редактирования, нажав на значок курсора на панели инструментов. Переходим в режим редактирования, двойным кликом по стержню открываем всплывающее окно, при необходимости изменяем граничные условия стержня (жёсткая связь, шарнир, подвижный шарнир для опорного конца) и его характеристики.
Переходим в режим редактирования, двойным кликом по стержню открываем всплывающее окно, при необходимости изменяем граничные условия стержня (жёсткая связь, шарнир, подвижный шарнир для опорного конца) и его характеристики. Основные понятия………………………………………………….
Основные понятия…………………………………………………. .
.