Расчет плоских ферм: Расчет ферм с примерами решения и образцами выполнения

24.01.1976 By alexxlab Разное Комментариев нет

Расчет плоских ферм: Расчет ферм с примерами решения и образцами выполнения

Содержание

Расчет ферм с примерами решения и образцами выполнения

Содержание:

Ферма и их расчет
Метод вырезания узлов
Метод Риттера
Расчет плоских ферм
Основные понятия о плоских фермах
Условие жесткости фермы
Статически определенные фермы
Метод вырезания узлов
Метод Риттера
Фермы. Способы определения усилий в стержнях ферм
Простейшие фермы
Определение усилий в стержнях фермы
Способ вырезания узлов
Способ Риттера

Фермой называется шарнирно-стержневая геометрически неизменяемая конструкция.

Плоская ферма – частный случай пространственной конструкции, у которой один из поперечных размеров либо мал по сравнению с другими размерами, либо не существенен для распределения внутренних усилий.

Реальная ферма, может не иметь идеальных шарнирных соединений в узлах, соединения стержней между собой в узлах являются жесткими, а не шарнирными, с помощью сварки, заклепок, болтов или других скреплений.

Плоские фермы конструируют таким образом, что приложенная к ферме нагрузка передается в узлах, вследствие чего, в сечениях элементов ферм не возникают поперечные силы и изгибающие моменты, стержень работает только на продольные усилия – растяжение или сжатие, и, следовательно, реакции стержней будут направлены вдоль этих стержней.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Ферма и их расчет

Ферма — это жесткая конструкция, которая состоит из прямолинейных стержней, соединенных между собой шарнирами. Место, где стержни соединяются друг с другом, носит название узла фермы. Внешняя нагрузка прикладывается к ферме только в ее узлах. Ферма состоит из идеальных стержней, то есть тонких, однородных, невесомых

стержней, на концах которых шарниры, которые работают на растяжение или на сжатие.

Мы будем рассматривать фермы, в которых оси всех стержней и векторы внешних сил содержатся в одной плоскости, то есть, плоские фермы. Помимо этого, конструктивно ферма состоит из стержней, которые образуют собой треугольники, то есть в конструкции фермы нет лишних стержней. такие фермы являются жесткими и статически определенными. В них число стержней n и число узлов m всегда связано таким соотношением

n = 2m – 3 .

Расчет фермы сводится к определению ее опорных реакций и усилий в стержнях.

Рассмотрим простую плоскую ферму (рис. 1.26).

Как видно из схемы — это плоская конструкция, которая состоит из 7 стержней, которые соединяются в 5 узлах. В узлах I и V ферма имеет опоры (в I-ом узле — неподвижная шарнирная опора; в V-м — подвижная шарнирная опора), к II и к IV узлу фермы приложены внешние нагрузки в виде сосредоточенных сил и ( = 30 kH; = 10 kH). Линейные и угловые размеры фермы данные на схеме (α = 45º).

Оси плоской декартовой системы координат I xy показаны на схеме фермы.

Первый этап расчета фермы — это определение ее опорных реакций. Определяют опорные реакции, рассматривая ферму в целом, как твердое тело с приложенными внешними силами. Тогда, условно освобождая ферму от связей (опор) и заменяя их соответствующими реакциями (в узле I это реакции _I, _I; в узле V — _V), имеем плоскую систему произвольных сил, для которой можно использовать условия равновесия и составить систему уравнений равновесия:

Из первого уравнения системы вычисляем неизвестную реакцию

X_I. она равна

X_I = P₂ = 10 kH.

Из последнего уравнения вычисляем реакцию R_V:

Далее, из второго уравнения является возможность вычислить последнюю неизвестную
величину Y_I. Она будет равняться

Y_I = P₁ – R_V = 30 – 5 = 25 kH.

Таким образом, вычислено искомые реакции опор фермы. Теперь необходимо определить неизвестные усилия в стержнях фермы. существует несколько способов определения этих усилий, графические и аналитические. Мы рассмотрим два аналитические методы:

метод вырезания узлов и метод сечений (или метод Риттера). Рассмотрим последовательно эти методы.

Метод вырезания узлов

Этот метод заключается в последовательном вырезании (мысленно) узлов фермы,
начиная с узла где совпадают два стержня с неизвестными внутренними усилиями. Таким образом, каждый узел — это плоская система сходящихся сил, для которой можно составить два уравнения равновесия, из которых определяют неизвестные усилия в этих двух стержнях.

При применении этого метода принимается правило, согласно которому реакции
стержней направляются от узлов. Если же при определении реакции стержня произойдет, что она имеет отрицательный знак, то этот стержень сжат и действительное направление его реакции ориентировано к узлу.

Определим данным методом усилия в стержнях фермы, приведенной на рис. 1.26. Вырезаем сначала узел I (рис. 1.27). Кроме реакций _I и _Iк нему приложены неизвестные реакции стержней 1 и 2, которые обозначаются и и направление которых, по правилу, от узла. Покажем в этом вырезанном узле I оси координат xIy и угол α. Как видно из схемы, узел и находится в равновесии под действием плоской системы сходящихся сил с двумя неизвестными усилиями: и . Составим для узла и уравнения равновесия,

используя условия равновесия для плоской системы сходящихся сил в виде. Будем иметь

Из второго уравнения определяем усилия S₁. Оно равно

Как видим, стержень 1 сжатый усилиям 35,3 kH. С первого уравнения определим неизвестное усилие S₂

S₂ = – X_I– S₁ sinα = –10 – (– 35,3 · 0,707) = – 10 + 25,00 = 15,00 kH .

Таким образом, стержень 2 растянутый усилием 15,00 kH.

Далее вырезаем узел ІІ (рис. 1.28). В этом узле сосредоточены внешняя сила и усилия трех стержней , и . Причем неизвестные усилия только в двух стержнях — в 3 () и в 4 (). Также предварительно считаем, что стержни 3 и 4 растянуты, и их усилия и
направлены от узла ІІ. Усилия же в стержне 1 уже определено ранее, при вырезании первого узла, и не только установлено его значение, но и то, что он сжат, поэтому направление его реакции будет к узлу ІІ. Проведем через узел ІІ оси координат xy и покажем угол α.

Составим для узла ІІ уравнения равновесия, также используя условия, аналогичные предыдущим.

Из второго уравнения определяем усилия S₃. Оно будет равняться

Как видим, стержень 3 сжатый усилиям 7,00 kH. Направление реакции S₃ — к узлу ІІ.

Из первого уравнения находим усилия S₄. Оно равно

S₄= –S₁sinα – S₃cosα = – 35,30 · 0,707 – (–7,00)0,707 = – 25,00 + 5,0 = – 20,00 kH.

Таким образом, стержень 4 сжатый усилием 20,00 kH.

Далее вырезаем узел IV (рис. 1.29). Он находится под действием внешней силы и усилий в стержнях 4, 5 и 7. Усилия в стержне 4 определено и его направление — к узлу, а потому неизвестны — только усилия и . Проведем через узел IV оси координат

xy и покажем угол α. Направления усилий в стержнях 5 и 7 — от узла IV. Составим для узла IV уравнения равновесия, также используя условия равновесия:

Решаем систему, для чего из второго уравнения выразим усилия S₅ через усилия S₇. Оно будет равняться

Теперь подставим значение S₅ в первое уравнение системы. Будем иметь

S₇ cosα – (– S₇)cosα – P₂ + S₄

= 0.

Отсюда

Стержень 7 сжатый усилием 7,00 kH. Теперь есть возможность найти усилие S₅. Оно равно

S5 = – S₇ = 7,00 kH.

Стержень 5 растянутый усилием 7,00 kH.

Теперь, для окончательного определения усилий в стержнях фермы, что рассматривается, необходимо вырезать узел V. К узлу V приложена реакция , усилия , которое направлено к узлу, и неизвестно усилию , которое направляем от узла. Составим для узла V уравнения равновесия, используя условия равновесия:

Как видим, для определения последнего неизвестного усилия S₆достаточно решить первое уравнение системы. Найдем S₆:

S₆ = S₇ cosα = 7,00 · 0,707 = 5,00 kH.

Стержень 6 растянутый усилием 5,00 kH.

Данные расчетов заносим в таблицу 1.1. Знак при определенном усилии в стержне показывает характер его нагрузки. Если он положительный («+»), То стержень растянут, если отрицательный («–»), то стержень сжат.

Метод Риттера

Рассмотрим второй аналитический метод определения усилий в стержнях плоской фермы. Это метод Риттера, или метод сечений.

Данный метод имеет несколько преимуществ по сравнению с рассмотренным ранее
методом вырезания узлов. Здесь нет необходимости составлять большое количество уравнений равновесия узлов, особенно когда ферма многостержневая. Кроме того, в случае неточности расчета какого-то стержня, в дальнейшем эта ошибка накапливается при расчетах других стержней. Метод Риттера лишен этих неудобств.

Особенность применения этого метода состоит в том, что условно делается сечение всей фермы, при этом в сечении должно быть не больше, чем три стержня с неизвестными усилиями. Тогда рассматривается равновесие одной из частей фермы, а вторая часть отбрасывается. Действие стержней, которые попали в сечение, заменяем их реакциями. предварительно считается, что эти стержни также растянуты, то есть их усилия направлены от узлов. Опорные реакции фермы определяются так же, как и при
применении метода вырезания узлов.

Определим усилия в 4, 5 и 6 стержнях фермы, сделав сечение и рассматривая равновесие правой части фермы (рис. 1.31). Вместо указанных стержней прикладываем в узле IV усилия и а в узле V — усилие . Направления указанных усилий — от узлов. К данной части фермы приложена внешняя сила и реакция . Покажем оси прямоугольной декартовой системы координат Vxy и угол α. Как видим, данная часть
фермы находится в равновесии под действием плоской системы произвольных сил, а
для этого составим для нее уравнения равновесия, используя условия равновесия. Согласно методу Риттера надо составлять уравнения равновесия, как суммы моментов сил относительно тех точек, где пересекаются линии действия большего количества неизвестных усилий. В данном случае такими точками будут точки ІІІ и IV. В отношении этих точек возьмем моменты сил.

Будем иметь

Вычислим неизвестные усилия. Из первого уравнения — усилия S₅:

Из второго уравнения — усилия S₄. Оно будет равняться

Таким образом, стержень 4 сжатый усилиям 20,00 kH, направление усилия S₄ будет противоположный тому, который был показан на рис. 1.31.

Расчет плоских ферм

Фермой называется конструкция, состоящая из стержней, соединённых между собой на концах шарнирами и образующих геометрически неизменяемую систему. Шарнирные соединения стержней фермы называют её узлами. Если оси всех стержней фермы лежат в одной плоскости, то ферма называется плоской.

Основные понятия о плоских фермах

Фермой называется геометрически неизменная конструкция, состоящая из прямолинейных стержней, соединенных в узлах шарнирами (рис. 8.1).

Основная задача, о которой будет идти речь далее, заключается в определении внутренних усилий, возникающих в стержнях фермы под действием внешних активных сил.

Приведенное определение фермы имеет одно существенное упрощение, которое позволяет усилия в стержнях фермы находить методами теоретической механики. Этим упрощением является допущение о шарнирном соединение стержней фермы.

В реальных фермах стержни соединены жестко с помощью электросварки, клепки и тому подобное. Однако, как показывают исследования в строительной механике, сделано допущение о способе соединения стержней фермы позволяет найти приближенное значение усилий с достаточной точностью.

Фермы используются в качестве несущих конструкций в различных сооружениях: в мостах, в перекрытиях зданий, в подъемных кранах, каркасах самолетов тому подобное.

Места соединения стержней фермы называются узлами, а те узлы, которыми ферма опирается на основу — опорными узлами. Стержни, размещены по верхнему контуру фермы, образуют верхний пояс, а по нижнем — нижний пояс (См. Рис. 8.1).

Вертикальные стержни называются стойками, а наклонены — раскосами.

Фермы бывают пространственные и плоские. Если оси всех стержней фермы лежат в одной плоскости, такая ферма называется плоской, если нет — то пространственной. В этом разделе ограничимся рассмотрением только плоских ферм.

Расчет ферм существенно упрощается, если сделать такие допущения:
1) трения в шарнирах отсутствует;
2) заданные силы, действующие на ферму, лежат в плоскости фермы и приложенные в узлах;
3) собственный вес стержней малый по сравнению с заданными силами и ею можно пренебречь.

Если выполнять эти условия, каждый стержень фермы будет работать на растяжение или сжатие и не испытывать деформации изгиба, в чем и есть преимущество фермы как строительной конструкции. Действительно, при условии, что все усилия приложены в узлах фермы и отсутствует трение в шарнирах, каждый стержень будет находиться под действием только двух сил, которые приложены к его концов. Согласно с первой аксиомой статики, при равновесии линия действия этих сил должна проходить через их точки приложения. Итак, силы, приложенные к стержню фермы, будут обязательно направлены вдоль стержня, и поэтому приводить его сжатие или растяжение.

Сделанные допущения оправданы тем, что, во-первых, трения в шарнирах малое по сравнению с заданными силами и им можно пренебречь; во-вторых, если сила приложена не у узле фермы, то ее можно разложить на составляющие, которые будут приложены в узлах.

Для того чтобы ферму можно было использовать как несущую конструкцию в инженерных сооружениях, необходимо обеспечить ее жесткость.

Определим условия, при которых ферма будет жесткой (геометрически неизменной).

Условие жесткости фермы

Найдем наименьшее число стержней N, необходимых для построения геометрически неизменяемой (жесткой) фермы, которая имеет n узлов.

Простой, геометрически неизменной фермой является конструкция, состоит из трех узлов, соединенных тремя стержнями. для жесткого присоединения каждого из последующих узлов необходимо два стержня (Рис. 8.2). Полученная таким образом новая конструкция также будет геометрически неизменной фермой.

Следовательно, для обеспечения жесткости фермы (т.е. исключения относительных
перемещений стержней) необходимо, чтобы число стержней равнялось

то есть

Пример неизменной жесткой фермы показано на рис. 8.3, а.

Если число стержней то конструкция будет геометрически переменной (рис. 8.3, б), а если то ферма будет содержать лишние стержни (рис. 8.3, в).

Уравнение (8.1) называется условием жесткости фермы. Заметим, что равенство (8.1) является необходимым условием жесткости фермы, но не достаточным. Для конструкции, изображенной на рис. 8.3, г, условие (8.1) выполняется, но эта система геометрически переменная. Для обеспечения геометрической неизменности фермы условие (8.1) должно выполняться как для всей фермы, так и для отдельных ее частей (решеток).

Статически определенные фермы

Статическую определенность фермы устанавливают по количеству реакций опор и числом стержней фермы.

Заметим, что ферма является неизменной системой, поэтому, как известно из предыдущего, неизвестных опорных реакций не должно быть более трех. В противном случае задача определения опорных реакций для данной фермы является статически неопределенной.

Рассчитывая фермы, кроме трех неизвестных реакций, нужно еще определить усилия в стержнях фермы. Выясним, сколько независимых уравнений статики можно составить для определения этих неизвестных сил. для этого используем метод вырезания узлов.

На каждый вырезанный узел фермы будет действовать плоская система сходящихся сил, которая состоит из внешних сил (активных и реакций связей) и внутренних усилий в стержнях. Поэтому система сил, приложенная к узлу, должна удовлетворять двум уравнениям равновесия

Следовательно, при равновесии фермы, которая имеет n узлов, все действующие на ферму
внешние силы и усилия в стержнях должны удовлетворять 2n уравнением.

С равновесия отдельных узлов фермы следует равновесие фермы в целом, а потому три уравнения равновесия записанные для всей фермы, будут линейными комбинациями первых уравнений, которые являются независимыми.

К 2n уравнениям будут входить три неизвестные реакции связей и внутренние усилия в стержнях. Из этих уравнений можно найти — неизвестных внутренних усилий в стержнях. Если число стержней фермы эти усилия могут быть определены из уравнений статики, и такая ферма называется статически определенной; если усилия в стержнях с помощью одних лишь уравнений статики абсолютно твердого тела определить невозможно и ферма будет статически неопределенной. Заметим, что условие жесткости фермы (8.1) действительно для плоской фермы и является условием статической определенности.

Методы нахождения усилий в стержнях статически неопределенных ферм рассматриваются в курсах сопротивления материалов и строительной механики. В курсе
теоретической механики рассматривают только статически определенные фермы.

Существует три основных метода нахождения усилий в стержнях статически определенных ферм: вырезания узлов Риттера и графический (построения
диаграммы Максвелла-Кремоны).
Остановимся только на двух аналитических методах.

Метод вырезания узлов

Суть метода вырезания узлов заключается в том, что рассматриваем равновесие каждого узла в отдельности. Для этого вырезаем узлы фермы, прикладываем к ним соответствующие внешние силы и реакции стержней и составляем уравнение
равновесия сил, приложенных к каждому узлу. Поскольку в начале расчета фермы неизвестно, какие стержни фермы растянуты, а какие сжаты, условно допускаем, что все стержни растянуты. В этом случае реакции стержней направляем от узлов. Если в результате вычислений получим значение реакций некоторых стержней со знаком минус, то это будет означать, что эти стержни сжаты. Найденные реакции стержней по модулю равны внутренним усилием в стержнях.

Последовательность рассмотрения узлов определяется по условию: число неизвестных сил, приложенных к узлу, не должно превышать количества уравнений равновесия сил, то есть двух.

Проиллюстрируем этот метод на конкретном примере.

Задача 1. Найти усилия в стержнях фермы, изображенной на рис. 8.4, методом вырезания узлов, если к узлу D фермы приложено вертикальную силу

Решение. В этой ферме число узлов n = 8, а число стержней N = 13. Итак, условие (8.1) выполняется и ферма является жесткой без лишних стержней, то есть статически определенной.

Составим уравнения равновесия для всей фермы и найдем реакции опор А и В:

Переходим к определению усилий в стержнях. Условно вырежем все узлы фермы, сохраняя последовательность, указанную выше. реакции стержней обозначим через (рис. 8.5). На основе закона равенства действия и противодействия

Для сил, которые совпадают в каждом узле, составим последовательно уравнения равновесия. Расчет начнем с узла А, в котором приложены только две неизвестные силы и

Равновесие последнего узла В можно не рассматривать, поскольку все усилия найдены. Если правильно найдены все усилия, то условия равновесия узла В будут выполняться тождественно.

Полученные усилия в стержнях 1, 4, 8 и 12 отрицательные, и это означает, что стержни сжаты.

Усилия в отдельных стержнях загруженной фермы, как видно из приведенного примера, могут равняться нулю. Такие стержни принято называть нулевыми.

Сформулируем леммы, которые позволяют найти нулевые стержни плоской фермы, не проводя ее расчета.

Лемма 1. Если в незагруженном узле плоской фермы сходятся два стержни, то усилия в этих стержнях равны нулю.
Лемма 2. Если в незагруженном узле плоской фермы сходятся три стержни, два из которых расположены на одной прямой, то усилия в третьем стержни равна нулю. Усилия в первых двух стержнях равны между собой.
Лемма 3. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилия в этом стержни равна по модулю приложенной силе, а усилия во втором стержне равна нулю.

Довести эти леммы предлагается самостоятельно.

Методом вырезания узлов выгодно пользоваться тогда, когда нужно найти усилия во всех стержнях фермы. Этот метод хоть и простой, но громоздкий и нерациональный в тех случаях, когда нужно найти усилия не во всех стержнях фермы, а только в отдельных. Например, для нахождения усилий только в одном стержне приходится рассматривать
последовательно равновесие определенного количества узлов, пока не будет найдено усилия в нужном стержни. Этот недостаток отсутствует в методе Риттера.

Метод Риттера

Метод Риттера состоит в том, что после нахождения реакций опор ферму условно разрезают на две части так, чтобы в сечении было не более трех стержней с неизвестными усилиями, и рассматривают равновесие одной из частей фермы. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, то есть считают, что стержни розтянути (как в методе вырезания узлов).

На часть фермы, которую рассматриваем в равновесии, будут действовать внешние силы и реакции разрезанных стержней. Для полученной плоской системы сил составляем три уравнения равновесия.

Уравнение выгодно записывать в виде равенства нулю суммы моментов всех сил относительно трех разных центров,которые являются точками, в которых попарно пересекаются разрезанные стержни или их продолжение. Эти точки носят название точек Риттера. В каждое из уравнений моментов относительно трех точек Риттера будет входить лишь одно неизвестное, а именно усилия в том стержни, ось которого через эту точку не проходит. Покажем это на примере.

Задача 2. Методом Риттера найти усилия в стержнях 4, 5 и 6 фермы, изображенной на рис. 8.4.

Решение.Реакции опор фермы найдены в предыдущем примере Условным сечением разделим ферму на две части по стержнях 4, 5, 6 (рис. 8.4) и рассмотрим равновесие левой от сечения части фермы.

Действие правой части на левую заменяем реакциями и(Рис. 8.6).

Для плоской системы сил, которая действует на левую часть фермы, составляем три уравнения равновесия:

где и — точки Риттера, которые показаны на рис. 8.6.

Индексация точек Риттера выбрана так, что уравнение моментов, записанное относительно каждой точки , содержит только одно неизвестное усилиев стержне под номером

Решая эту систему уравнений, получим:

Величины найденных усилий совпадают с полученными ранее методом вырезания узлов.

Аналогично можно найти усилия и в других стержнях фермы. Из приведенного примера видно, что уравнение равновесия не связаны между собой, а потому для нахождения усилий в одном стержне достаточно составить лишь одно из этих уравнений.

Фермы. Способы определения усилий в стержнях ферм

Основными способами определения усилий в стержнях ферм являются: — способ вырезания узлов; — способ сечений Риттера; — графический способ определения усилий в стержнях фермы с помощью построения диаграммы Максвелла-Кремоны; — метод построения веревочного многоугольника.

Простейшие фермы

Фермами называются конструкции, которые состоят из прямолинейных стержней, которые соединены между собой шарнирами и образуют неизменную геометрическую фигуру (рис. 4.1). При расчете ферм весом стержней пренебрегают и считают, что шарниры размещены только на концах стержней; нагрузки, действующие на ферму, приложенные в шарнирах (т.е. в узлах фермы). В этом случае каждый стержень фермы испытывает усилия, действующие вдоль оси стержня, то есть будет растянут или сжат.

С всего класса геометрически неизменных ферм без лишних стержней выделим простые фермы. Их построение происходит так: рассматривается основной треугольник, к нему двумя стержнями присоединяется новый шарнир (узел) и и. д. В дальнейшем будем изучать простые, плоские фермы, где их стержни расположены в одной плоскости.
По своему назначению зачастую фермы делятся на мостовые, стропильные и крановые (рис. 4.1). Установим зависимость между количеством стержней и количеством шарниров (узлов) в простых фермах.
Рассуждаем так: для образования основного треугольника нужно три стержня и три шарнира. Для образования каждого из остальных шарниров (узлов) необходимо два стержня для постоянного соединения с основой фермы. Итак, общее количество стержней в простой ферме с учетом трех стержней основного треугольника определяется так:

(4. 1)

Основной задачей расчета простых ферм является определение усилий в стержнях фермы, которые являются внутренними силами, возникающими в стержнях под действием внешних сил. Эту задачу можно решить методами теоретической механики.

Определение усилий в стержнях фермы

Ограничимся двумя способами определения усилий в стержнях простой фермы: способом
вырезания узлов (графически-аналитический метод) и способом Риттера (аналитический метод).

Способ вырезания узлов

Этот способ заключается в том, что каждый узел вырезается из
фермы и рассматривается отдельно как таковой, что находится в равновесии под действием приложенных к нему внешних сил и усилий разрезанных стержней. Система сил, действующей на узел, является плоской системой сходящихся сил, которая находится в равновесии; следовательно, силовой многоугольник, построенный из этих сил, должен быть замкнутым. Построение силовых многоугольников (треугольников) следует начинать с узла, в которых сходятся два стержня, тогда построением замкнутого треугольника (третья сторона отвечает известной заданной силе, прилагаемой в узле) найдутся усилия в этих двух стержнях.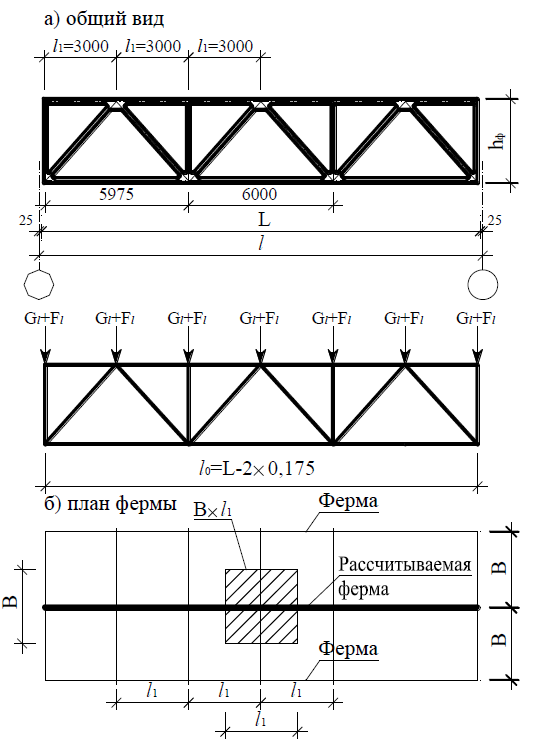 После этого можно переходить к следующему узлу и т. Д. Каждый следующий узел выбирается так, чтобы в нем сходилось не более двух стержней с неизвестными усилиями. Так графически будут определены усилия во всех стержнях. Если усилия разрезанных стержней направлены по стержнях в сторону узла, то они сжимающие, в противном случае — растяжимые.
Формально условия равновесия узлов фермы включают в себя условия равновесия фермы в целом, то есть позволяют найти и внешние реакции. Более того, предварительное определение внешних реакций фермы существенно упрощает решения задачи. Рассмотрим способ вырезания узлов на примере расчета усилий в стержнях фермы, показанной на рис. 4.2.

Пример 1. В узле В фермы приложена сила Опорами фермы будут шарнир А и каток С. Определить: реакции опор , усилия стержней в узлах А и D.
Решение. Рассмотрим ферму как твердое тело, которое находится в равновесии под действием плоской системы параллельных сил (в этом случае реакция шарнира будет параллельная силам и , иначе система сил , а следовательно, сама ферма не была бы в равновесии). Проведем ось параллельно силам системы и составим условия равновесия в виде (3.21)

откуда найдем

Определение усилий в стержнях начнем с рассмотрения узла А, в котором сходятся два стержня: 1 и 7. Строим замкнутый треугольник из сил , (рис. 4.2). Для этого в соответствующем масштабе строим вектор, равный вектору реакции , с конца которого проводим прямую, параллельную стержню АВ, а с начала — прямую, параллельную стержню AD. С построенного треугольника находим усилия и . Изображая эти усилия в узле А, видим, что направлено к узлу А по стержню АВ, следовательно, оно — тяговое, а усилия S7 направлено от узла А по стержню AВ, то есть оно — растяжимое. Растяжимое усилия обозначается знаком плюс, а сжимающее — знаком минус. Теперь рассмотрим равновесие сил в узле , в котором остаются только две неизвестные силы: и .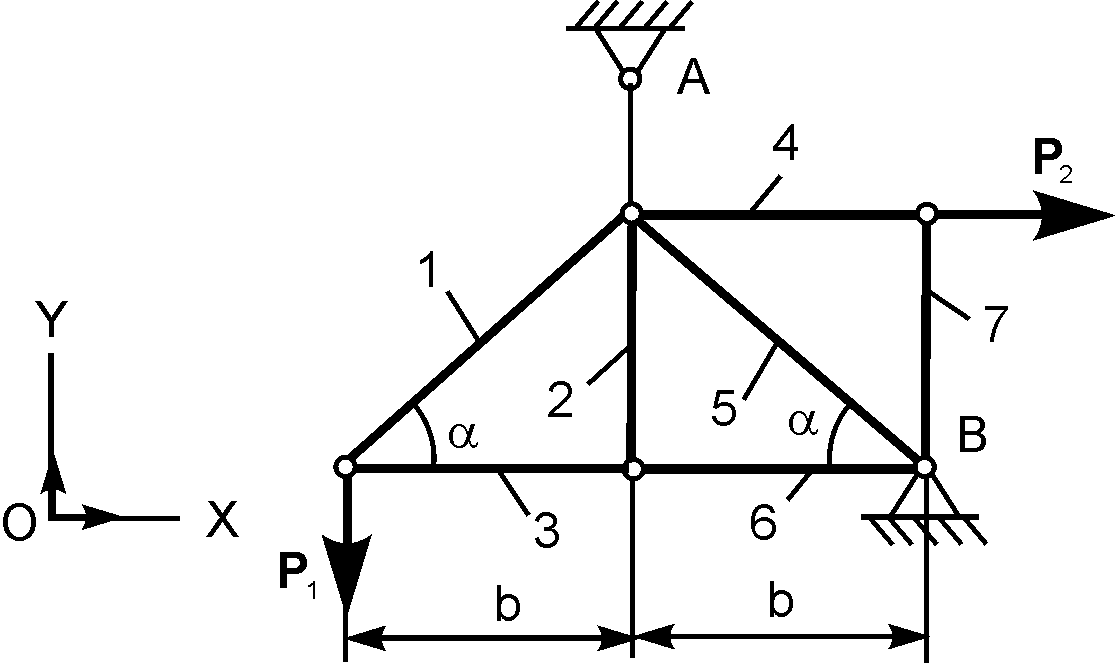 Реакция стержня 7, который выходящий из узла равна и противоположная по направлению его же реакции, но приложена в узле А. Опять строим замкнутый треугольник сил: откладываем силу , с ее конца проводим прямую, параллельную стержню 2, сначала — прямую, параллельную стержню 6, и определяем величины и направления усилий и . Аналогично можно определить другие усилия:

Неудобство этого способа заключается в его громоздкости, поскольку приходится строить столько многоугольников, сколько узлов в ферме. Объединение разных многоугольников сил в одну диаграмму осуществили независимо друг от друга английский физик Максвелл и итальянский геометр Кремона, в честь которых эту диаграмму назван диаграммой Максвелла — Кремоны.

Способ Риттера

Этот способ позволяет найти усилия в любом стержни фермы независимо от усилий в других стержнях. Однако предварительно необходимо определить реакции опор фермы.
Способ Риттера состоит в том, что ферма рассекается на две части так, чтобы в сечении было не более трех стержней с неизвестными усилиями, которые не сходятся в одном узле. Отвергая отсеченную часть фермы и рассматривая равновесие той части, оставшейся под действием приложенных внешних сил и усилий, которые заменяют действие рассеченных стержней, получим для этой части фермы три уравнения равновесия с тремя неизвестными усилиями. Чаще всего эти уравнения являются условиями равенства нулю алгебраических сумм моментов сил относительно трех разных центров моментов, за которые выбирают точки парного пересечения рассеченных стержней с числа перерезанных. Эти точки называются точками Риттера.
Если два стержня из трех рассеченных параллельны, то одна точка Риттера удаляется в бесконечность. Тогда составляют два уравнение моментов сил и одно уравнение проекций сил на ось, перпендикулярную к параллельным стержням.

Пример 2. Определить усилия в стержнях 1, 2, 3 фермы, если а другие размеры показано на рис. 4.3.
Решение. Найдем реакции в опорах фермы и . Реакция катка В направлена по нормали к опорной плоскости, а поскольку на ферму действует система параллельных сил то и реакция шарнира А будет параллельной этим:

Отсюда находим Проведем сечение через стержни 1,2,3 и рассмотрим равновесие той части рассеченной фермы, в которой приложено меньшее количество сил. В рассматриваемом случае — это правая часть фермы. Усилия в рассеченных стержнях условно считаем растяжимыми и направлением в сторону части, отбрасываются. Итак, в отсеченной части фермы уравновешивается плоская система сил

Для определения усилия соответствующей точкой Риттера будет точка К, а уравнение равновесия примет вид:

Для определения усилия точкой Риттера является точка В, для определения усилия — точка D, а соответствующие уравнения равновесия имеют вид:

Подставляя необходимые данные, находим
Итак, усилия — растяжимое, — сжимающее (тяговое) , — нулевое (при заданной нагрузке стержень 2 не работает, но с конструкции его изъять нельзя, поскольку нарушится жесткость конструкции и не выполнится условие (4.1)). В завершение сравним методы Максвелла — Кремоны и Риттера, несмотря на их различие, которое заключается в том, что первый метод относится к графическим, а второй — к аналитическим. Как видно из предыдущего изложения, усилия методом вырезания узлов определяются последовательно, переходя от одного узла к соседнему. Поэтому неизбежно накопление ошибок, связанных с неточностью проведение параллельных прямых. Следует отметить, что накопление этих ошибок можно избежать при решении задачи чисто аналитическим способом, составляя уравнения равновесия для системы сходящихся сил, приложенных в узлах фермы.

Но, с другой стороны, взаимосвязь между построением новых вершин диаграммы Максвелла — Кремоны и положением предыдущих, следует рассматривать как определенное ограничение погрешностей, позволяет избежать грубых
ошибок.
Метод Риттера в отличие от предыдущего не приводит к накоплению ошибок, так как все усилия определяются независимо друг от друга, но одновременно не дает возможности заметить грубые ошибки, которые могут случиться при исчислении.

Очевидно, лучшая методика определения усилий в стержнях фермы заключаться в сочетании методов Максвелла — Кремоны и Риттера. Например, все усилия определяются по методу Максвелла — Кремоны и некоторые из них проверяются методом Риттера.

Услуги по теоретической механике:

Заказать теоретическую механику
Помощь по теоретической механике
Заказать контрольную работу по теоретической механике

Учебные лекции:

Статика
Система сходящихся сил
Момент силы
Пара сил
Произвольная система сил
Плоская произвольная система сил
Трение
Расчет усилий в стержнях фермы
Пространственная система сил
Произвольная пространственная система сил
Плоская система сходящихся сил
Пространственная система сходящихся сил
Равновесие тела под действием пространственной системы сил
Естественный способ задания движения точки
Центр параллельных сил
Параллельные силы
Система произвольно расположенных сил
Сосредоточенные силы и распределенные нагрузки
Кинематика
Кинематика твердого тела
Движения твердого тела
Динамика материальной точки
Динамика механической системы
Динамика плоского движения твердого тела
Динамика относительного движения материальной точки
Динамика твердого тела
Кинематика простейших движений твердого тела
Общее уравнение динамики
Работа и мощность силы
Обратная задача динамики
Поступательное и вращательное движение твердого тела
Плоскопараллельное (плоское) движение твёрдого тела
Сферическое движение твёрдого тела
Движение свободного твердого тела
Сложное движение твердого тела
Сложное движение точки
Плоское движение тела
Статика твердого тела
Равновесие составной конструкции
Равновесие с учетом сил трения
Центр масс
Колебания материальной точки
Относительное движение материальной точки
Статические инварианты
Дифференциальные уравнения движения точки под действием центральной силы и их анализ
Динамика системы материальных точек
Общие теоремы динамики
Теорема об изменении кинетической энергии
Теорема о конечном перемещении плоской фигуры
Потенциальное силовое поле
Метод кинетостатики
Вращения твердого тела вокруг неподвижной точки

Расчет ферм

К вопросу о расчете плоских ферм (приложение к дискуссии)

Расчет фермы на прочность по способу вырезаний узлов довольно громоздкий. Расчет состоит из таких этапов (по Леоненко Д. В.):

1.Определение реакций опор фермы путем составления уравнений равновесия относительно точек опор:

2.Поочередно вырезаются узлы, в которых сходятся пояса (верхний и нижний), стойки и раскосы решетки фермы. Проектируя усилия на координатные оси хоу определяют характер (сжатие или растяжение) и величину усилий в стойках, раскосах и поясах панелей фермы. Таких узлов для фермы с тремя стойками и двумя раскосами –восемь:

3. По полученным результатам расчетов строится опора продольных сил во всех элементах фермы. Исходя из эпюры сил переходят к расчету прочности элементов фермы и подбору сечений этих элементов. Следуя технологичности изготовления фермы, при выборе сечения элементов принимают за расчетное максимальное усилие (например, в нижнем растянутом поясефермы действуют усилия 425 кГс, 425 кГс, 550 кГс, 375 кГс, следовательно, в расчет берут 550 кГс). Используя классическую формулу,

определяют напряжение в элементах фермы или момент сопротивления профиля (W), если определены положения, с последующим выбором определенного профиля из сортамента профилей.

Этот расчет классический и может применяться для расчета ответственных ферм в строительстве.

Если возникает необходимость запроектировать молонагруженную ферму для укрытия или козырька входа, когда на ферму действует снеговая нагрузка, ветровая нагрузки и собственный вес, можно рассматривать ферму, как балку с разнесенным сечением и следовательно расчет существенно упрощается что ведет к значительной экономии средств в малых предприятиях занимающихся металлоконструкциями.

В качестве примера можно привести способ увеличения несущей способности балки путем рассечения ее по стойке с последующей сваркой частей балки со смещением в местах примыкания (см. схему).

Такой способ применяли для производства панелей покрытия и стеновых панелей при строительстве быстромонтируемых зданий производственного назначения.

Определяем величину увеличения несущей способности балки после ее рассечения и сварки.

Стандартный профиль балки №30.
Балка рассеченная, сварная

Видно, что момент сопротивления балки в 4,3 раза, а значит возросла ее несущая способность.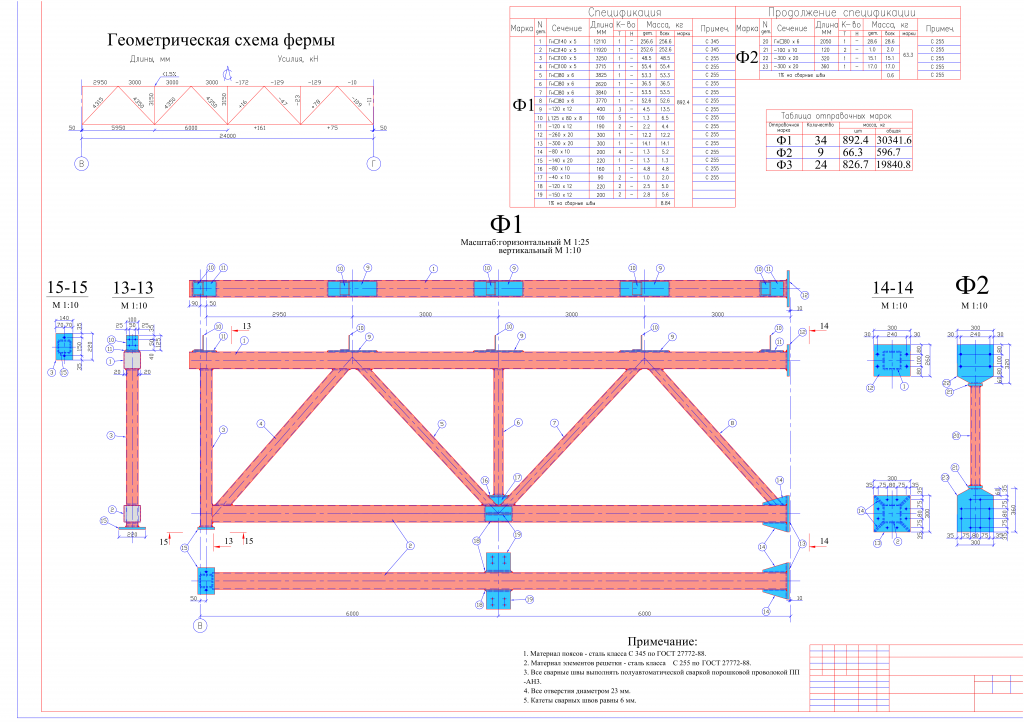

Рассмотрим упрощенный расчет фермы из профильных труб (нижний и верхний пояса), стойки и раскосы из листового проката или труб меньшего поперечного сечения:

Сечение фермы в точке приложения сечения силы: используем формулу для определения момента сопротивления относительно оси Х (сопромат, табл. 1, стр. 37).

Определив изгибающий момент от действия Р вычисляется напряжение в нижнем (растянутом) поясе формы.

Где – допускаемое напряжение для материала (Сталь 3)
– момент сопротивления сечения составил 510,6 см3.

Для сравнения момент сопротивления двутавровой балки №30е (ГОСТ 8239-56) составляет 518 см3 (сопромат, табл. 6, стр. 90).

Рассмотрим расчет фермы из круглих труб (нижний и верхний пояса), стойки и раскосы из листового материала (или профильного) проката:

Сечения фермы в точке приложения силы Р будет. Используем известную методику определения момента сопротивления сложного сечения.

Где I – момент инерции трубчатого сечения. (сопромат, стр. 55, таб.1)

ymax – максимальное удаление поперечного сечения трубы от главной оси Х – Х.
(сопромат, стр. 21)

Определив изгибающий момент от действия силы Р, определим напряжение в нижнем (растянутом) поясе фермы.

Где – допускаемое напряжение для материала (Сталь 3)
Wx – момент сопротивления сечения составил 110,4 см3.

Для сравнения момент сопротивления двутавровой балки №22 (ГОСТ 8239-56) составляет 230 см3 (сопромат, табл. 6).

Рассмотрим расчет фермы из профильных труб прямоугольного сечения. Используем известную методику определения момента сопротивления сложного сечения.

Общий момент сопротивления будет относительно оси Х – Х.

(сопромат, стр. 31)

где

Общий момент сопротивления будет относительно оси х-х:

Рассчитав момент сопротивления сечения, можно определить напряжение в нижнем поясе фермы и выбрать необходимый профиль.

Выводы

1. Классический расчет фермы позволяет определить усилия во всех элементах фермы, однако он сложный и м.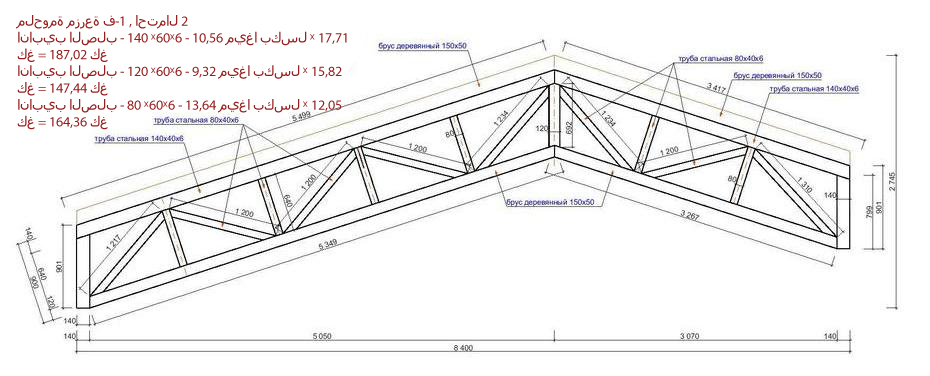 б. использован при расчете ответственных конструкций.
2. Упрощенный расчет фермы дает возможность определить прочностные характеристики опоеного сечения фермы и выбрать необходимые профили нижнего и верхнего поясов фермы.

Ткаченко Н.А. зам главного конструктора » ТОВ Стальмира «

Использованные источники
1.    Г.С. Писаренко и др. Справочник по сопротивлению материалов. К. 1975г.
2.    С.П. Фесик. Справочник по сопротивлению материалов. К. 1982г.
3.    Д.В. Леоненко. Расчет плоских ферм. Б: 2006г.

Error

Sorry, the requested file could not be found

More information about this error

Jump to… Jump to…ГОСТРАБОЧИЕ ТЕТРАДИУЧЕБНЫЕ ПОСОБИЯТеоретический материал Начертательная геометрия.Теоретический материал Инженерная графика (инженерная и компьютерная графика).ОбъявленияДОЛГИ (выполненные задания) загружать сюда Теоретический материал БИ-21И1Задания по Инженерной и компьютерной графике БИ-21И1 Титульный лист для отчета по РГРЗадания АТб-21А1/А2Задания по Инженерной графике (ТЛб-21Z1)Задание по Начертательной геометрии (ТЛб-21Z1)Задание по инженерной графике ЭУб-21Z1ТЕСТ к ЭКЗАМЕНУ — ЭУб-21Z1Задания по Начертательной геометрии (ЭУб-21Z1)Лекция № 1 Образование проекций. Лекция № 2 «Основные правила выполнения чертежей»Лекция № 3 «Проекции плоскости»Лекция № 4 «Сечения»Лекция 4.1 Сечение поверхности плоскостьюЛекция № 5 «Сложные разрезы»Лекция № 6 «Виды изделий»Лекция № 7 «Выполнение эскизов деталей машин»Лекция 8 «Проекции с числовыми отметками» ГОСТы, которые Вам помогуЗадания по Начертательной геометрии и инженерной графики (ГЕОб-21Z1)Итоговый тест ГЕОб-21Z1Графические работы АПб-21Z2Вопросы к экзаменуТЕСТ к ЭКЗАМЕНУ — АПб-21Z1/АПб-21Z2Теоретический материал Задание на графические работы по дисциплине «Компьютерная графика» Учебное пособиеНачертат геом установка ШИИЛекция 2Указания по выполнению заданийОформление работ заочниковГрафическая работа «Проекции с числовыми отметками»Графическая работа «Арх.- строит. чертеж здания»Отправка заданийГеометрическое компьютерное моделирование (Автокад) Отправка задания «ВАЛ» и «СОПРЯЖЕНИЕ»Отправка задания «План здания» (ГЕОб-20Z1)Задание для зачетаГрафическая работа № 1 Чертеж ВалаГрафическая работа № 2 СопряжениеГрафическая работа № 3 Проекционное черчениеВАЛСопряжениеРазвязкаЛекция 5 Кривые линии и поверхностиЛекция 6 Сечение поверхности плоскостью, построение развертокЛекция 7 Пересечение прямой с поверхностямиФлэш-плеер 1Флэш-плеер 23,4 и 5 темы загружать сюдаЛЕКЦИИ ЭУб-20А1ЗАДАНИЯ НА РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫТитульный лист для отчета по РГРРешенные задачи (1 к. н.) загружать сюдаГрафическую работу № 0 загружать сюда Задание Графическая работа № 1Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 1 загружать сюдаРешенные задачи (3 к.н.) загружать сюдаЗадание Графическая работа № 2Графическую работу № 2 загружать сюдаГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаГр. работа 5. Эскиз зубчатого колесаГр. работа 6. Эскиз штуцераГр. работа 7. СоединенияГр. работа 8. ДеталированиеЛекция 2Лекция 4Лекция 5Лекция 6Лекция 7Лекция 8Macromedia Flash PlayerСписок 1й подгруппы группы АТб-20Z1Список 1й подгруппы группы АТб-20Z2Теоретический материалГрафические работыОтправка графических работ АТб-20Z1/АТб-20Z2Теоретический материалЗадание на графические работы по дисциплине «Компьютерная графика» АТб-20Z1/АТб-20Z2Учебное пособие для ЗаочниковЛекция часть 1Лекция часть 2Лекция часть 3Задание для ЗаочниковОтправка выполненных чертежей1. Теоретический материал 2. Проекционное черчение3. Компьютерное черчениеОтправка заданий на весенний семестрЭкзамен ЭУб-20Z1/ЭУб-20Z21. Теоретический материал Задание по инженерной и компьютерной графике1. Теоретический материал Задание по инженерной графикеГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Наклонное сечениеГр. работа 4. ИзометрияГр. работа 5. Эскиз валаГр. работа 6. Винтовая параГр. работа 7. Эскиз штуцераГр. работа 8. Эскиз зубчатого колесаГр. работа 9. ПриводВопросы к экзамену по Начертательной геометрииИнструкция для прохождения интернет-тестирования 11.01.2021 в 10:00Список студентов записанных на интернет-тестированиеMacromedia Flash PlayerЛекция 7Лекция 8Лекция 9Задание Графическая работа № 0Решенные задачи (1 к.н.) загружать сюдаГрафическую работу № 0 загружать сюда Задание Графическая работа № 1 Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 1 загружать сюда Задание на графическую работу № 2Решенные задачи (3 к.н.) загружать сюдаГрафическую работу № 2 загружать сюдаФото отчета пройденного теста загружать сюдаТема 8Тема № 9Лекция ПЧОЗадание графическая работа № 1Решенные задачи (1 к. н.) загружать сюда Графическую работу № 1 загружать сюда Задание Графическая работа № 2 Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 2 загружать сюдаЗадание Графическая работа № 3Решенные задачи (3 к.н.) загружать сюда Графическую работу № 3 загружать сюдаЗадание Графическая работа «Проекции с числовыми отметками»Теоретический материалГОСТыГрафическая работа № 1Графическая работа № 2Графическая работа № 3 (ЭСКИЗ)Гр. работа № 4 План этажа зданияТеоретический материал по теме (компьютерная графика)1. Проекционное черчение (Сложный разрез)2. Сопряжение.3. СлоиВилкаВкладышВыполненные чертежи Вилки и Вкладыша загружать сюда (копия)Методические указания к работеИсходные чертежиВыполненную работу загружать сюдаТема 8Задание графическая работа (Инженерная графика)Решенные задачи (1 к.н.) загружать сюда Графическую работу (Инженерная графика) загружать сюда Задание Графическая работа № 2 Решенные задачи (2 к.н.) загружать сюда Графическую работу № 2 загружать сюдаЗадание ГР № 3Решенные задачи (3 к. н.) загружать сюда Графическую работу № 3 загружать сюдаЗадание Графическая работа № 4 «Проекции с числовыми отметками»Решенные задачи (1 к.н.) загружать сюдаГрафическую работу загружать сюдаЗадание Графическая работа № 1Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 1 загружать сюдаЗадание Графическая работа № 2Решенные задачи (3 к.н.) загружать сюдаГрафическую работу № 2 загружать сюдаГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаГр. работа 5. Эскиз зубчатого колесаГр. работа 6. Эскиз штуцера Гр. работа 7. СоединенияГр. работа 8. ДеталированиеЗадания для должников ГЕОб-20Д1Задание графическая работа № 1Решенные задачи (1 к.н.) загружать сюда Графическую работу № 1 загружать сюдаГрафическая работа № 2 (исходные чертежи)Графическая работа № 3 (задание)Решенные задачи (2 к.н.) загружать сюда Графическую работу № 2 загружать сюдаГрафическую работу № 3 загружать сюда Решенные задачи (3 к.н.) загружать сюда Задание Графическая работа № 3Графическую работу № 3 загружать сюдаЗадание Графическая работа № 4 «Проекции с числовыми отметками»Задание на графическую № 5 работу «Проекционное черчение»Графическую работу № 5 «Проекционное черчение» загружать сюдаГрафическая работа № 1Решенные задачи (1 к. н.) загружать сюдаГрафическую работу №1 загружать сюдаРешенные задачи (2 к.н.) загружать сюдаГрафическую работу № 2,3 загружать сюдаЭСКИЗ Решенные задачи (3 к.н.) загружать сюдаГрафическую работу «Эскиз» загружать сюда Задание «Проекционное черчение»Графическую работу «Проекционное черчение» загружать сюдаЗадание Привод* Выполненные чертежи «Привод» загружать сюдаЗадание 3D модель 2* Выполненный чертеж «3D модель 2» загружать сюдаСоединенияГрафическая работа № 1Решенные задачи (1 к.н.) загружать сюдаГрафическую работу №1 загружать сюдаРешенные задачи (2 к.н.) загружать сюдаГрафическую работу № 2, 3 загружать сюдаЭСКИЗРешенные задачи (3 к.н.) загружать сюдаГрафическую работу «Эскиз» загружать сюда Задание «Проекционное черчение» Графическую работу «Проекционное черчение» загружать сюда Занятие НТС-19Т2 15:25 27.05.2020Занятие CМб-19Т1 08:20 21.05.2020Занятие НТС-19Т2 15:25 20.05.2020Лекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации. Лекция 2 Сечения.Лекция 3 Сложные разрезы.Лекция 4 Виды изделий. Разъемные и неразъемные соединения. Выполнение сборочных чертежей.Лекция 5 Выполнение эскизов деталей машин.Лекция 6 Деталирование чертежа общего вида.Курс лекций Инженерная графика презентацияТеоретический материал———ГОСТы, которые Вам помогутВыполненные графические работы и эскизы загружать сюдаСодержание работыРазъемные и неразъемные соединения (теория)Методические указанияВарианты (согласно списку в журнале *у старосты*)Исходный чертежПример выполнения сборочного чертежа «Привод»Пример выполнения спецификации «Привод»Пример выполнения чертежа «Корпус»Пример выполнения спецификации «Корпус»Пустые листы спецификацииВыполненные чертежи по заданию «Разъемные и неразъемн…» загружаем сюдаТеоретический материал——-Методические указания (Эскиз)Выполненные эскизы загружать сюдаВарианты заданияОбразецВыполненный чертеж винтовой пары загружать сюдаПринятые обозначения Лекция 1. Образование проекций. Метод Монжа. Проекции точки и прямой. Лекция 2. Проекции плоскоти. Прямая линия и точка в плоскости.Лекция 3. Взаимное положение плоскостей. Взаимное положение прямой и плоскости.Лекция 4. Способы преобразования чертежа. (Метрические задачи)Лекция 5. Кривые линии и поверхности.Лекция 6. Сечение поверхности плоскостью. Построение разверток поверхностей.Лекция 7. Пересечение прямой линии с поверхностями.Лекция 8. Взаимное пересечение поверхностей.Лекция 9 Аксонометрические проекцииВыполненный чертеж загружать сюдаРабочая тетрадь Решенные задачи загружать сюдаКарточки с исходным чертежом на ГР № 1 (по вариантам)Карточки с исходным чертежем на ГР № 2 (по вариантам)Методические указания по выполнению графических работПример выполнения ГР № 1Пример выполнения ГР № 2Загружать на проверку Графическую работа № 1 сюдаЗагружать на проверку Графическую работа № 2 сюдаТЕСТТеоретический материал Инженерная графика (инженерная и компьютерная графика)ГОСТы, которые Вам помогутГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаТеоретический материал по теме (компьютерная графика)Разъемные и неразъемные соединения (теория)Исходный чертежПример выполнения сборочного чертежа «Привод»Пример выполнения спецификации «Привод»Выполненные чертежи Привода загружать сюдаВыполненный чертеж редуктора загружать сюдаГр. работа 6. Эскиз штуцера (копия)Лекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.Теоретический материал—ГОСТы, которые Вам помогутГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаТеоретический материал по теме (компьютерная графика)ЗАДАНИЕ (исходный чертеж)Выполненный чертеж поршня загружать сюдаВилкаВкладышВыполненный чертеж поршня загружать сюдаЛекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.Лекция 2 Сечения.Лекция 3 Сложные разрезы.Лекция 4 Виды изделий. Разъемные и неразъемные соединения. Выполнение сборочных чертежей.Лекция 5 Выполнение эскизов деталей машин.Лекция 6 Деталирование чертежа общего вида.Курс лекций Инженерная графика презентацияТеоретический материал—-ГОСТы, которые Вам помогутГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа № 3 ЭСКИЗЛекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.Лекция 2 Сечения.Лекция 3 Сложные разрезы.Лекция 4 Виды изделий. Разъемные и неразъемные соединения. Выполнение сборочных чертежей.Лекция 5 Выполнение эскизов деталей машин.Лекция 6 Деталирование чертежа общего вида.Курс лекций Инженерная графика презентацияТеоретический материал——-ГОСТы, которые Вам помогутВыполненные графические работы и эскизы загружать сюдаСодержание работыРазъемные и неразъемные соединения (теория)Методические указанияВарианты (согласно списку в журнале *у старосты*)Исходный чертежПример выполнения сборочного чертежа «Привод»Пример выполнения спецификации «Привод»Пример выполнения чертежа «Корпус»Пример выполнения спецификации «Корпус»Пустые листы спецификацииВыполненные чертежи по заданию «Разъемные и неразъемн. ..» загружаем сюдаТеоретический материал——Методические указания (Эскиз)Выполненные эскизы загружать сюдаПоследовательность выполнения работыТеоретический материал——Образец (пример)Задания по вариантамВыполненный чертеж железобетонной конструкции загружать сюдаЗанятие 13:45 27.05.2020Занятие 13:45 20.05.2020Занятие 15:25 15.05.2020Теоретический материал по теме (компьютерная графика)ВилкаВкладышВыполненные чертежи Вилки и Вкладыша загружать сюдаМетодические указания к работеИсходные файлыВыполненную работу загружать сюдаТеоретический материал по теме (компьютерная графика)ВилкаВкладышВыполненные чертежи Вилки и Вкладыша загружать сюдаМетодические указания к работеИсходные чертежи -Выполненную работу загружать сюдаЗАДАНИЕ (инженерная графика)Теоретический материал (инженерная графика)Задание № 1 загружать сюдаЗадание № 2 загружать сюдаЗадание № 3 загружать сюдаЗадание № 4 загружать сюдаТеоретический материал (компьютерная графика)Деталь № 1Деталь № 2Деталь № 3Деталь № 1 загружать сюдаДеталь № 2 загружать сюдаДеталь № 3 загружать сюдаЗанятия 1-4 (16. 06.2020 15:25 — 21:50)Занятия 5-6 (20.06.2020 13:45 — 16:55) ЭКЗАМЕНТеоретический материал Начертательная геометрияУказания к выполнению графических работРешения задачОтправка выполненных заданийТеоретический материал Начертательная геометрияУказания к выполнению графических работРешения задачОтправка выполненных заданийЧертеж для занятия 13.11.2020ЗАДАНИЯ-Теоретический материал по теме (компьютерная графика)* Выполненные чертежи (1 файлом) загружать сюдаКонтроль выполнения ЗАДАНИЙ

Skip Accessibility

(always?)

Skip Statistics

Расчет ветровой нагрузки на ферму крыши согласно IS 875-2015

27 апреля 2022 г. 24 октября 2020 г.

В этой статье мы объясняем расчет ветровой нагрузки на ферму крыши в соответствии с пересмотренными нормами 875-2015. Объяснены все этапы расчета ветровой нагрузки с решенным примером. Так что читайте статью до конца и комментируйте, если что-то не так в этой статье.

Содержание

Ступени стропильной фермы Расчет ветровой нагрузки в соответствии с 875-2015.

Шаг-1: Угол фермы крыши

Угол фермы крыши = tan ^-1 ( Высота/(Размах/2))

Базовый ветер 02 (V b )

Определение базовой скорости ветра на странице № 6 или 51 IS 875 часть-3-2015 по местонахождению.

Шаг 3: Расчет давления ветра

1. Расчетная скорость ветра (V _z ):

0007

V _z = V _b × K ₁ ×K ₂ × K ₃ × K ₄

Where,

V _b = Basic wind speed
K ₁ = Коэффициент риска
K ₂ = Коэффициент шероховатости и высоты местности
K ₃ = Фактор топографии
K ₄ = Коэффициент важности для циклонического региона

= ОЧИЧЕСКИЙ СПОСКИ 875 Часть 3

Базовая скорость ветра на высоте 10 м для некоторых важных городов Индии согласно части 3 875 2015 года приведена в таблице ниже.

9011 м/с .

0094

City/Town	Basic Wind Speed	City/Town	Basic Wind Speed
Agra	47m/s	Kanpur	47m/s
Ахемадабад	39 м/с	Кохима	44 м/с
Ajmer	47m/s	Kolkata	50m/s
Almora	47m/s	Kozhikode	39m/s
Amritsar	47m/s	Kurnool	39m/s
Asansol	47m/s	Lakshadeep	39m/s
Aurangabad	39m/s	Lucknow	47m/s
Bahraich	47m/s	Ludhiyana	47m/s
Bengaluru	33m/s	Madurai	39m/s
Barauni	47m/s	Mandi	39m/s
Bareilly	47m/s	Mangalore	39m/s
Bhatinda	47m/s	Moradabad	47m/s
Bhilai	39m/s	Mumbai	44m/s
Bhopal	39m/s	Mysore	33m/s
Bhubaneshwar	50m/s	Nagpur	44m/s
Bhuj	50m/s	Nainital	47m/s
Bikaner	47m/s	Nashik	39m/s
Bokaro	47m/s	Nellore	50m/s
Chandigarh	47m/s	Panjim	39m/s
Chennai	50m/s	Patiala	47m/s
Coimbatore	39m/s	Patna	47m/s
Cuttack	50m/s	Punducherry	50m/s
Darbhanga	55m/s	Port Blair	44m/s
Darjeeling	47 м/с	Pune	39M/S
Dheradun	47M/S		39M/S	101103	39m/S /S	14/S /S	4/S 9010/S /S	4/S /S 9010/S 9010/S	Delhi	47m/s	Rajkot	39m/s
Durgapur	47m/s	Ranchi	39m/s
Gangtok	47 м/с	Roorkee	39 м/с
Guwahati	50 м/с 0111111111111111111111111111111111111111011011111111111111111111111111111111010101011111111111010 гг.0108
Gaya	39m/s	Shimla	39m/s
Gorakhpur	47m/s	Srinagar	39m/s
Hyderabad	44m/s	Surat	44m/s
Imphal	47m/s	Tiruchirappalli	47m/s
Jabalpur	47m/s	Trivandrum	39m/s
Jaipur	47m/s	Udaipur	47m/s
Jamshedpur	47m/s	Vadodara	44m/s
Jhansi	47m/s	Varanasi	47m/s
Jodhpur	47m/s	Vijayawada	50m/s
Vishakapatnam	50m/s

Find K ₁

K ₁ получен из стр. № 7, таблица-1, IS 875 часть-3 2015
K1 зависит от класса и срока службы конструкции.

Найти K ₂

K ₂ зависит от категории местности и высоты конструкции.
Категория местности определяется на основе местности расположения сооружения.
K ₂ получен по сравнению с Таблица 2, стр. № 8, IS 875 Часть 3 2015

Найти K ₃

K ₃ Получен из. стр. № 8, IS 875 часть-3 2015.

Найти K ₄

K _{4 получено} Из пункта № 6.3.4, страница № 8, 875 Часть 3 2015.
для госпиталей , Schools
для госпиталей , Schools
для госпиталей , Schools
. , укрытия от циклонов, K ₄ 1,30.
Для промышленных конструкций К ₄ равен 1,15.
Все остальные конструкции, K ₄ 1,00.

2. Расчетное давление ветра:
P _D = K _D × K _A × K _C × P _Z
, где,
P _Z = Давление с ветром
P _Z = ветровый давление
P _{8. _z ²}
K _d = коэффициент направленности ветра
K _a = коэффициент усреднения по площади.
K _c = комбинированный коэффициент.
Найти K _d
K _d берется из п. 7.2.1 стр. 9, IS 875 часть-3 2015. № 10, IS 875 часть-3 2015.
Ка зависит от притока .
Площадь притока = расстояние или шаг × подъем
Find K _c
K _c получен из пункта № 7. 3.3.13 9002 , страница №16, IS 875 часть-3 2015 .
Этап-4: Ветровая нагрузка на отдельные элементы
Ветровая нагрузка на отдельные элементы определяется по формуле, приведенной в МС 875 ч. 3 п. 7.3.1 стр. 10.
F = ( C _PE — C _PI) A × P _D
Где,
C _PE = Коэффициент внешнего давления
C _PI = Коэффициент внутреннего давления
A = СОЗВОДИТ блок облицовки
P _d = design wind pressure
Find C _pi
C _{pi is obtained} from clause 7.3.2, page no 11, IS 875 part 3 2015.
C _pi зависит от площади отверстия в конструкции.
Найти C _PE
C _PE Получен из пункта 7.3.3, Page № 11, 875 Часть 3 2015.
C _PE также получайте Таблицу 6. , IS 875 часть-3 2015.
Решаемый пример расчета ветровой нагрузки по ГОСТ 875-2015
Система кровли промышленного навеса состоит из ферм, расположенных на расстоянии 6 м друг от друга. Пролет стропильной фермы 18 м, высота 3 м. Уровень карнизов 7 м над землей. Предположим подходящую конфигурацию фермы. Тень расположена на равнинной местности с малонаселенной застройкой. Проницаемость сарая менее 20%. Подготовьте конструктивный макет промышленного стального сарая подходящей конфигурации. Определить силы ветра на ферму. Расположение Ченнаи.
. Данные:
Расстояние: 6M
SPAN = 18M
Восстание = 3M
Высота = 7M
Террена: плоская местность с Sparsely Gopulated
Shed Sheds менее 20%. Решение:
Предположим, что ферма Howe типа для пролета 18 м.
Шаг-1: Угол фермы крыши
Угол фермы крыши = tan ^-1 ( Подъем/(Размах/2))
= tan ^-1 (3/(18/2))
= 18,43
Шаг 2: Определение базовой скорости ветра (V _b )
Для Ченнаи базовая скорость ветра составляет 50 м/с от страницы №51, IS 875 часть-3 2015.
Этап-3: Расчет ветрового давления
Непосредственное нахождение К ₁ , К ₂ , К _3,-35 ИС К 7 _{9 из 9 9 . Для нахождения этого коэффициента объяснено выше по шагам.}
К ₁ = 1
K ₂ = 1
K ₃ = 1
K ₄ = 1.15
V _z = V _b × K ₁ ×K ₂ × K ₃ × K ₄
= 50 × 1 × 1 × 1 × 1.15
= 57.5m/s
Design Wind Pressure:
P _d = K _d ×K _a × K _c × P _z
Прямой поиск K _д, К _а, К _с из ИС 875 часть-3. Для нахождения этого коэффициента объяснено выше по шагам.
K _d = 0.9
K _a = 0.92 (getting this by interpolation between 10 and 25)
K _c = 0. 9
P _z = 0.6 × V _z ²
= 0,6 × 57,5 ²
=1983,75 Н/м2
P _d = K _d ×K _a × K _c × P _z
= 0.9 × 0.92 × 0.9 × 1983.75
= 1478.29 N/m2
= 1.478 KN/m2
Design wind pressure is less чем 0,7 × p _Z
= 0,7 × 1983,75
= 1388,62 (N/M2) Следовательно,
Step-4: ветровая нагрузка на отдельные члены
F = (C _PE –C. _pi ) A × P _d
Найти C 9(0,5)) / 8)
= 7,115 M2
Следовательно,
A × P _D _{= 7,115 × 1,478}
= 10,52 КН
Расчет ветровой нагрузки.
Силы, действующие на гравитационную плотину | Компоненты | Критерии проектирования
Каковы роли инженера-строителя в строительстве
Трещины в бетоне | Типы | 7 основных причин | Средства правовой защиты | РРТ
Débouchage canalisation Montpellier-SOS-Débouchage 34
Sans frais de déplacement autour de Montpellier dans un rayon de 30 km
06. 66.87.59.99
Vraiment plus un service, d’d’désa on qualité ils une Heure à déboucher mes Toilettes qui avaient débordées. Des personnes vraiment très gentilles qui sont venus à 22h régler mon problème et qui n’ont pas lâché l’affaire jusqu’à ce que ce soit résolu, plus d’une heure et demi plus tard. Vraiment un grand merci
Je suis particulièrement satisfait de l’intervention du technicien de débouchage 34. Благодать за настойчивость и пугливость, il a réussi à régler notre problème. Il est rester jusqu’à minuit, il n’a rien lacher pour aller au bout de son Professionalnalisme. Браво Луи. Поздравление с сыном-покровителем лучших работодателей.
Appel pour un débouchage le matin et вмешательство dès l’après-midi, très réactif et professionalel. De très bons conseils, très efficace et une gentillesse, редкий chez les dépanneurs de nos jours. Surtout avec de jeunes Adultes comme nous, qui rantrons dans le monde de l’indépendance. Je recommande vivement et rappellerai pour sûr! Житель данс уне дом коммуна авек plusieurs студии, ноус пенсии дие ноус авион causé le bouchon данс ла канализации. Étant notre première expérience avec les services de dépannage nous avions eu peur de nous faire arnaquer. Mais pas du tout. Dès l’appel, le prix était déjà fixé. Et très amical, il nous a directement mit en confiance. Il nous a bien expliqué que ce n’était pas de notre faute mais celui du réseau qui a plus de 50 ans. Il nous a ensuite montré et expliqué en détail le problème et plusieurs façons pour pouvoir le régler. Il ensuite était très raisonnable sur le prix. Rien à redire, j’en parlerais tout autour de moi et donnerais leur nom quand on me requireera si je connais de bons plombiers.
L’intervenant était tres gentil, respectueux et donne des conseils volontiers. J’ai appelé le matin pour un débouchage des canalisations, j’ai eu une вмешательство dans l’après-midi. Le rapport qualité prix est plus que правильный. Aucun сожаление, je les recontacterai pour sûr!
Tarik a été au top, реактивный, сердечный, профессиональный и проблемный в 1 час! Je recommande absolument, et merci! 🙂
Серьезный труд, правильный и профессиональный результат. Je ne peux que recommander.
Трес профессионал, ils connaissent très bien leur domaine.
Au top⭐️⭐️⭐️
Канализация Débouchage Montpellier et ses alentours
Devis Бесплатное вмешательство и срочное вмешательство в отношении RDV 7J/7 et 24/24 sans majoration
Plombier, un déboucheur avec tout le matériel adapteré
Dépannage Rapide et dans l’heure
Eviers, lavabos, душ, baignoire, WC, égout.
Полная диагностика и взаимопонимание: определение проблемы, локализация бушона, определение уровня пенте
Прозрачность, бесплатно
Professionnel du Дебушаж Монпелье
Demander conseil à votre artisan Plombier Montpellier
Débouchage canalisation à votre domicile dans l’heure qui suivent votre appel.
Intervention d’un camion pompe haute pression à prix intéressant, pour le curage, le nettoyage de vos install sanitaire sur Montpellier
Дебушаж мануэль
Демонтаж санитарного сифона
Ручная помпа или механическая помпа
Гидрокураж Débouchage высокого давления
Система высокого давления без химикатов
Полная сетка для канализации
Видео осмотр канализации
Инспекция с камерой высокого разрешения на 100 м
ENTREPRISE DÉBOUCHAGE MONTPELLIER
Vous avez un bouchon ? Nous avons la решение!
Depuis 2004, nous proposons nos services de débouchage canalisation à Montpellier aux particulier et Professionalsnels qui souhaitent benéficier d’un service professional et de de qualité.
Toute l’équipe de DEBOUCHAGE 34 à Montpellier vous garantit toujours:
Быстрое вмешательство: nous intervenons dans l’heure qui suit votre appel téléphonique
Общая доступность и прозрачность: вы можете связаться с нами в течение 24 часов в течение 24 часов и 7 дней в течение 7 дней, если вы хотите, чтобы канализация была закрыта
Des tarifs qui défient toute concurrence: nous proposons des prix très avantageux , n’hésitez pas à requireer votre devis бесплатно
24h/24 et 7j/7
sans majoration
Pas de frais
de déplacements
Artisans Qualifiés
et Agréés
Service & Appel Technicien
Avis vérifiés де нет клиентов
ТАРИФЫ DEBOUCHAGE CANALISATION MONTPELLIER
Туалетные наборы
Сифон
Душ/беньюар
Лав-Вассель
Эвакуация
Машина для умывания
Pour ce forfait nous utilisons selon votre install un déboucheur révolver base pression, un furet mecanique (professionnel).
Канализация Nettoyage
Дебушаж
Детартраж
Лекарство
Camion débouchage haute pression
Оценка
Grâce à notre véhicule, nous pouvons intervenir dans les lieux inaccessibles pour les camions d’assainissement. Nous disposons d’un furet de 100 mètres, d’une puissance de 350 bar.
Сос дебушаж канализация Монпелье
Plombier Débouchage Pas cher
Туалет, Lavabo, Evier, Douche, Tout a l’egout…
Канализация камеры осмотра
Камион Помпе Монпелье
Информационное исследование
Вмешательство 24H/24 et 7J7 без мажорации де тарифа Авангард 20H
Служба проверки клиентов
Une tres grande reactivité.
Невероятная эффективность (непригодные для использования кухня/столовая).
Une cordialité vraie malgré la hardé du travail.
Des prix fixs et tres corrects.
Bref, je recommande les yeux fermés et je reviendrais si besoin, même si j’espère que ce ne sera pas trop vite!
PAUL LEBACC Положительные аспекты: вежливость, качество связи, реактивностьhttps://g.page/thplomberie34?gm – google
J’ai eu besoin d’un plombier pour une fuite de ma chaudière ainsi que l’entretien qui n’avait pas été fait depuis un определенных темп. J’ai choisi TH Plomberie au vu des commentaires élogieux et franchement je n’ai pas été déçue: Reactivité, compétence et prix correctes, gentillesse en plus, rien à redire
Мари Мишель Положительные аспекты: пунктуальность, качество, качество связи, реактивностьhttps://g.page/thplomberie34?gm – google
Le souhait comme tous de trouver le bon artisan qui pratique des prix raisonnables. Celui dont les gestes sont sûrs, образец профессионализма. Son seul soucis, Que le résultat soit au delà de vos attentes. Et bien monsieur, merci et encore merci de posséder toutes ces qualités. C’est rassurant pour l’avenir de pouvoir compter sur vous…. »
ab bouferrou Положительные аспекты: Оперативность, Качество, Раппорт, качество-цена, Реактивностьhttps://g.page/thplomberie34?gm – google
PLOMBIER DEBOUCHAGE CANALISATION MONTPELLIER
Vous constatez des problèmes d’evacuation au niveau de vos équipements sanitaires?
Equipes de Plombier debouchage Montpellier, travaillent en permanence dans le but d’intervenir et de mettre fin à tous vos ennuis.
Le débouchage des canalisations est un travail sale, long et malodorant que vous préférez ne pas faire vous-même. Заместитель слушателя по поводу серьезной проблемы, il vaut mieux faire appel à une entreprise de débouchage professionalnel.
Plomberie Depannage, канализация Монпелье 24:34
Un tuyaux engorgée ou bouchée est un problème courant en plomberie .
Pour résoudre les problèmes de refoulement d’eau et de mauvaises odeurs, faites appel à nos services.
Qu’il s’agisse d’evacuation, d’éviers, de WC ou de tout autre système d’eau, notre équipe intervient pour réparer vos appareils sanitaires.
L’équipe de débouchage 34 используйте автомобиль высокого давления 4×4. Grâce à leur expérience, ils peuvent recommander la meilleure solution pour le problème ciblé.
SOS DÉBOUCHAGE MONTPELLIER
Plombier d’urgence 24h/24 et 7 jours/7 sur Montpellier

L’équipe plombier Montpellier travaillent en permanence dans le but d’intervenir et de mettre fin à tous vos ennuis et vos problèmes d ‘Assainissement afin de vous satisfaire par une perfecte qualité de service, n’hésitez pas à nous contactez en cas ou vous aurez besoin de nos excelences prestations.
Avant l’intervention, nous diagnostiquons l’équipement sanitaire bouché afin de déterminer les причины набухания. Nous pouvons procéder à une инспекционное видео для устранения аномалий. Nous Effectuons ensuite le débouchage des conduits obstrués. La Maîtrise техника и le matériel исполнительских sont nos atouts.
Entreprise de debouchage canalisations Montpellier
Des canalisations engorgées peuvent ralentir l’écoulement de l’eau et provoquer des mauvaises odeurs. Dès que vous constatez ces signes, faites aussitôt appel à nous pour inspecter le réseau et déterminer l’origine des problèmes. Nous pouvons intervenir à temps pour éviter l’engorgement total de vos canalisations. Nous ferons en sorte que vous disposiez d’un réseau Performant.
Установка револьверного ключа, механическая установка (профессиональная).
Débouchage Montpellier
Garantie d’une Qualité de prestation de très haut niveau ainsi que la compétivité des délais d’evention 24h/24 D’ -et de ro -réalisation de opération elle soit l’origine des bouchons представляет dans vos tuyaux.
Les Experts de notre équipe représentent des points forts qui nous permettent de fournir des prestations rapide et en urgence 24h/24 et 7j/7.
Disponible 24h/24 et 7j/7 , en Urgence ou sur rendez-vous rapide – nos tarifs sont clairs et notre service de débouchage de canalisation fiable et quicke.
SOS Débouchage Montpellier
NOS NERSTESE PRESTATIONS DE Dégorement Canalisation à Montpellier Sont Disponibles à votre veu n ‘importe où vous êtes à montpellier
1317 où vous êtes à montpellier
où vous êtes à Montpellier
où vous à Montpellier
. , Castelnau Le Lez , Assas, Teyran, Pérols, Laverune, Castrie, Clapiers, Vendargues, Mauguio, Fabregues , Jacou,
58559 9125. équipes de Plombiers débouchages travaillent en permanency dans le but d’intervenir et de mettre fin à tous vos ennuis et vos problemes de plomberie afin de vous satisfaire par une perfecte qualité Débouchage canalisation sur Montpellier et de Degorgement canalisation , n’hésitez pas à nous contactez en cas ou vous aurez besoin de nos excelences prestations.
Nos équipes de Plombiers spécialiste du débouchage canalisations a Montpellier travaillent 24/24 dans le but d’intervenir et de mettre fin à tous vos ennuis et vos problemes de канализация .
Afin de vous satisfaire par une превосходное качество обслуживания Dégorgement , n’hésitez pas à nous contactez en cas ou vous aurez besoin de nos prestations avec nos camions de débouchage haute pression .
ВИДЕОКАНАЛИЗАЦИЯ ИНСПЕКЦИИ
Основные санитарные и канализационные системы sont frequemment bouchés malgré l’intervention d’un Professionalnel? Il peut y avoir une anomalie dans votre réseau d’égouts.
Специализированная компания по нападению на канализацию в Монпелье, с инспекционным видео на мобильную камеру с обзором на 360° по кругу. Nos techniciens effectuent un pré-nettoyage sous pression pour une meilleure visibilité.
Камион высокого давления
Канализация Détarrage
Détection fuite d’eau
Dé-racinage des tuyaux.
Видео осмотра
Пломбери.
Покушение.
10 лет опыта
Деви бесплатно без помолвки
вынос 7j/7
Быстрое вмешательство
Ремесленники Plombiers Reconnus
Быстрое вмешательство
Персональные советы
Канализация Débouchage Montpellier haute pression
Дегоржаж для полной канализации
Pour toute urgence de canalisations intérieures ou extérieures bouchées, DEBOUCHAGE 34 intervient chez vous 24h/24 et 7j/7 sur Montpellier et ses environs 30 kms .
Коммюнике по жалобам на тарифы, предназначенное для рассмотрения апелляционных жалоб.
Канализация Débouchage, Туалет Débouchage – Débouchage tout à l’égout – Проходная камера – Канализация Video – Plombier débouchage – Канализация bouchée 9Глава 12 в главе рассматриваются вопросы, связанные с определением членов силы внутри моста и связанные с ними напряжения. Начальный обсуждение сосредоточено на общем анализе фермы, а затем подразделы касаются компонентов системы перекрытий и моста крепление. В главе 13 обсуждаются вопросы, связанные со сравнением расчетные напряжения с допускаемыми напряжениями.
Тяжелые деревянные фермы ведут себя совсем иначе, чем более обычные, тяжелые стальные фермы. Элементы деревянных ферм в основном подвергаются осевым усилиям, как и во всех ферменных конструкциях, но они также подвержены значительным дополнительным нагрузкам от изгиба и поперечные силы. Статическая нагрузка стержня способствует некоторому сдвигу и реакция на изгиб, но балки перекрытия в точках промежуточных панелей и элементы, непрерывные через соединения, также создают внутренний сдвиг силы. Последним и основным источником этих неосевых сил является присущая многим традиционным деревянным столярным изделиям эксцентричность схемы подключения. В отличие от стальных ферм, где соединения изложен, чтобы включить теоретическую точку пересечения для члена центроиды, тем самым сводя к минимуму эксцентриситеты, тяжелая деревянная ферма столярные изделия часто не предусматривают общей точки. Оригинал строители сделали это по ряду веских причин. Традиционная столярка включает удаление материала по крайней мере с одного члена в каждом соединении создать связь с другим участником в этом суставе. Этот представляет собой неизбежный компромисс в качестве члена. Искусство проектирования и детализации традиционных деревянных столярных изделий заключается в смягчение и балансировка пагубного воздействия удаления древесины волокна от различных вовлеченных членов. Один классический способ сбалансировать ущерб состоит в том, чтобы разбросать различных участников или ввести некоторые незначительные эксцентричности при связях между более чем двумя членами. Проектировщики тяжелых деревянных ферм распределяют повреждения и создают лучшая структура, одна с более прочными соединениями между двумя элементами на время, растянутое по длине хотя бы одного из связанных члены.
Стальные фермы в значительной степени произошли от деревянных ферм особенно способами, которые не только упростили конструкцию, но и также в формах, упрощающих анализ и проектирование тяжелых фермы. Соединения в стальных фермах, идеализированные с их теоретические рабочие точки (то есть, где центроиды и силы членов параллельны), могут быть проанализированы только для осевых сил и рассчитаны соответственно. Даже строгие компьютерные аналитические методы, включающие местный изгиб, вызванный собственным весом элемента и незначительной собственной эксцентриситеты — в сочетании с осевыми силами — еще обычно привести к уровням напряжения, приемлемым для той же самой конструкции. Соблазн проводить более сложные современные анализы без реализуя какое-либо конкретное преимущество, демонстрирует оригинальное Преимущество стальных ферм в том, что они легко анализируются только осевые силы.
Другой способ описать это так: тяжелые деревянные фермы могут быть более точно смоделированы как кадры. Анализ кадров обычно осуществляется с помощью современного программного обеспечения. К сожалению, классические методы анализа рук распределения моментов и виртуальные работа почти прошла. Оценка тяжелых деревянных компонентов и конструкции при сочетаниях нагрузок и переменной продолжительности могут быть трудоемко и утомительно, даже с помощью современных методы. Кроме того, во многих случаях непреодолимая сложность типичный вывод компьютерного анализа может привести к несоответствующим упрощение или рационализация. Вдумчивый аналитик может сделать вывод, что допущения, сделанные в ходе моделирования тяжелая деревянная рама/ферма для компьютерного анализа может ввести неопределенности находятся в пределах разрешения предполагаемого полученные результаты.
Чтобы проиллюстрировать это, на рис. 89 приведен пример кадра соединения дуги Берра. Обратите внимание, как диагонали пересекают стойки на значительном расстоянии вниз от верхнего пояса. Несмотря на то что беспорядок различных элементов скрывает это, та же геометрия существует внизу постов. Это сильно отличается от обычная металлическая ферма с шарнирным соединением.
Рис. 89. Типичное эксцентриковое соединение в деревянная ферма (Браунс-Ривер-Бридж, Уэстфорд, штат Вирджиния, до недавнего реабилитация).
По этим причинам часто бывает хорошей идеей для современного аналитик, чтобы вернуться к основам анализа фермы и исследовать поведение конструкции деревянной фермы только на основе осевых сил, предполагая, что ферма имеет теоретические и концентрические рабочие точки. Учитывая относительно простые результаты этого крупномасштабного анализа, особенности отдельных элементов, подвергаемых более крупным комбинациям различные силы и напряжения могут быть наложены для конкретных изучение.
Например, конфигурация деревянной фермы, запатентованная полковником Стивен Лонг в 1830 году собрал из всех деревянных компонентов, с главные диагонали и фишки в каждой панели. Вертикали Длинные фермы подвергаются осевым растягивающим усилиям и значительным изгибающие напряжения из-за внецентренной нагрузки по диагоналям относительно расположения хордовых сил. Длинная ферма может быть довольно быстро проанализированы ручными методами, используя метод разрезы или метод соединений, если аналитик также готов временно пренебречь действием счетчиков.
Конечно, есть место и для более тонкого анализа, но базовый анализ крытого моста не должен быть особенно трудный или сложный.
Упрощенный анализ ферм
Как обсуждалось выше, тяжелые деревянные фермы часто можно анализировать адекватно, используя упрощенную модель конструкции. типовая продольная ферма крытого моста обычно строится с элементы хорды одинаковой глубины и размера по всему пролету. Данный эта призматическая компоновка, определяющая максимальную хордовую силу, может быть так же просто, как оценить моменты в середине пролета и учесть мост как простая и однопролетная конструкция. С этими упрощая предположения, максимальная хордовая сила для статически определенная ферма — это просто осевой момент в пролете, деленное на расстояние по вертикали между элементом пояса центроиды.
Другое упрощение, которое может быть очень полезным при оценке крытые мостовые фермы связаны с использованием пластинчатой балки аналогия. Продольные фермы можно идеализировать как глубокие балки. с большими отверстиями в паутине. В рамках этой упрощенной модели Силы полки в идеализированной плоской балке представляют собой хорду сил. Свойства сечения заменителя плоской балки: определяется по площадям и вертикальным расстояниям между различные элементы хорд и теорема о параллельных осях. Хотя это простое упрощение пластинчатой балки, оно тем не менее вполне достаточен хотя бы для предварительного оценка тяжелой деревянной фермы.
Уточненный анализ фермы
Когда более точное решение кажется оправданным при анализе древесины фермы, может быть принят компьютеризированный подход. Самый распространенный современный программное обеспечение использует метод конечных элементов. Это программное обеспечение может использовать сложные отдельные элементы для моделирования различных компонентов в деревянная ферма. Отдельные элементы могут быть размером с один элемент фермы или может быть размером с кубик, используемый в настольной игре. Как правило, чем меньше по размеру (и больше по количеству) элементов, тем точнее и точнее будет анализ. Пока этот анализ по своей сути не сложен и предлагается в все более удобные версии, тем не менее он остается имеет решающее значение для правильного моделирования условий поддержки и подключения поведение. Именно связи могут сделать компьютерную модель такой сложный.
Например, решетчатые элементы фермы Town обходят каждый другой, с двумя или тремя штифтами в однократном сдвиге между слоями доски на каждом перекрестке. Точный способ смоделировать это состоит в том, чтобы обе доски проходят через двойной узел в каждом стыке, а затем ввести фиктивный член между двумя узлами доски. этот манекен Элемент имитирует пружинное соединение между двумя досками. Аналитик должен правильно попытаться смоделировать связь привязки с срезной элемент и вращательные пружины, делая разумное предположение о жесткость рисунка штифта.
Поскольку эти сложные модели могут быстро стать подавляющее, даже для сегодняшнего оборудования, это все еще довольно распространено использовать структурную симметрию и готовить модели только частей всего моста, может быть, половины или четверти конструкции. Тогда становится особенно важным смоделировать опору условия должным образом на искусственных внутренних интерфейсах. Дальше, легко запутаться относительно симметричного, асимметричные и антисимметричные условия нагружения.
На рисунках 90 и 91 изображен трехмерный компьютер. Моделирование городского моста с решетчатыми фермами. Рисунок 90 демонстрирует полная стержневая модель конструкции в ненагруженном состоянии. На рис. 91 изображено аналогичное трехмерное изображение, искаженное от Эффект загрузки. На момент написания этой работы в середине 1990-х гг. считалось, что это компьютерное моделирование было самым сложным когда-либо предпринимались для крытого моста.
Рисунок 90. Трехмерное изображение компьютерное моделирование-без нагрузки. Обратите внимание на короткие поперечные элементы у пересечения ферменных решеток, изображающие туннель соединители.
Рисунок 91. Трехмерное изображение компьютерная симуляция-искаженная от нагрузки.
Следующий шаг в оценке достоверности любого теоретического анализ включает в себя сравнение результатов компьютерного моделирования с измеренным поведением реальной конструкции при фактических нагрузки. Одна простая проверка включает сравнение (1) измеренные отклонения в конструкции в определенных местах, в то время как конструкция загружена транспортным средством известного веса и конфигурация против (2) предсказанной компьютерной модели прогибов в одних и тех же точках и при одних и тех же нагрузках. Однако, даже если прогибы выгодно отличаются, это не гарантирует что фактические силы в конструкции равны компьютерным прогнозы для одних и тех же сил. Тензометрические датчики использовались для длительное время для измерения напряжений и сил в металлоконструкциях. Они также использовались, хотя и реже, при установлении структурная реакция в бетонных конструкциях. Тензодатчик замеры на полноразмерных элементах тяжелых деревянных мостов не распространены; тем не менее, возможно, что будущая работа в этом области позволит сравнивать компьютерные прогнозы и полевые проверка.
По многим из этих причин проектировщики и аналитики должны тщательно обдумайте, стоит ли пытаться провести уточненный анализ структура. Это медленный процесс и может быть дорогостоящим. Тем не менее, изысканный компьютерный анализ может быть очень полезным и целесообразным в некоторых экземпляры, такие как:
Окончательный проект проекта реабилитации после первоначального работать с использованием более простых методов анализа.
Оценка элементов, которые, как представляется, находятся в серьезном бедствии и для которых базовые методы анализа не могут обеспечить достаточная уверенность.
Подготовка к полевым нагрузочным испытаниям.
Комбинированная ферма и арка Анализ
Наиболее распространенным типом ферм крытого моста, сохранившимся до сих пор, является который поддерживается арками Burr, комбинация, обобщенная как ферма шкворня с наложенной аркой. Есть взаимосвязей по пролету сооружения, между аркой на с обеих сторон зажатой фермы, часто состоящей из одного болт в двойном сдвиге на каждой стойке через арки. Следовательно две фермы и арки разделяют общую нагрузку на мост. Общие вопросы: «Какая часть собрания несет какую долю от этой общей нагрузки? Выдерживает ли каждый из них половину нагрузки? Если не, сколько нагрузки какого типа приходится на каждый элемент, и почему?»
Некоторые считают, что первоначальные строители предназначали ферму для поддержки вся приложенная нагрузка, т. е. арки обеспечивают только сжатие устойчивость к продольному изгибу фермы. Другие считают, что ферма предназначался для поддержки только статической нагрузки, а арка там была для поддержки живой загрузки. Любое утверждение может быть поддержано.
Решение для распределения нагрузки внутри этого типа конструкции без компьютер утомительный и не особенно практичный. Однако, используя компьютерная программа разумна только при тщательном выполнении. Много Арочные конструкции с заусенцами демонстрируют значительные повреждения в местах крепления болтами. взаимосвязи между арками и стропильными стойками, указывающие тот или иной элемент недостаточно силен, чтобы нести предполагаемая доля нагрузки. Если соединение искажено или не удается, то жесткостные свойства самого соединения должны быть тщательно отобраны и смоделированы для компьютерного анализа имеют какое-то реальное значение.
Чтобы еще больше усложнить ситуацию, классическая дуга Burr включает в себя компоненты, которые опираются на опоры моста. Это вводит проблема, связанная со стабильностью абатмента при сопротивлении значительные толчки. Если опоры смещаются под арки’ тяга, затем тяга ослабляется, и на элемент фермы воздействуют перераспределяются. Есть и другие модифицированные арочные конструкции Burr в арка которого не поддерживается упорным блоком на абатменте но вместо этого заканчивается на нижнем хорде. Если соединение между арками и нижним поясом достаточно, арка может быть считается «привязанным». Однако, если анкерное соединение не удается, арка не может предложить большую поддержку нагрузки для конструкции, но имеет тенденцию вносят вклад только в плоскостную жесткость на изгиб и внеплоскостные устойчивость к изгибу.
Эта комбинация деревянной фермы с соединенными арочными элементами вероятно, одна из самых сложных поддерживающих систем противостоящие инженерам крытого моста. Тщательный осмотр, осмотр, и исследование ряда таких структур указывают на множество изменчивость, что делает обобщения нецелесообразными. Один очень критический и сложное допущение моделирования связано с жесткостью соединение между арками и фермой. В любом случае каждый из этих мостов заслуживает тщательного рассмотрения и оценки. Пример тяжелой деревянной арки Берра с зажатой фермой показана на цифра 92. На рис. 93 представлен пример деревянной фермы с легкая асимметричная арка. Непонятно, что, если есть, помощь, которую эта арка оказывает ферме.
Рисунок 92. Тяжелая деревянная арка Burr-Wehr Бридж, округ Лихай, Пенсильвания.

Рис. 93. Только прикрепленная легкая дуга на внутреннюю часть моста фермы Солсбери-центр, Херкимер округ, штат Нью-Йорк.
Влияние балочных балок
Как указано в главе 7 в разделе «Болистерные балки», подпорные балки часто настолько прочны, что могут обеспечить некоторые опора фермы за лицевой стороной устоя (см. рис. 94), тем самым эффективно сокращая теоретический диапазон ферма. На рис. 95 показан пример бетонной опоры.
Рис. 94. Большая поперечная балка, опирающаяся на подшипниковые блоки-Hall Bridge, Rockingham, VT.
Рис. 95. Валик из Бетон-Виллидж или Большой вихревой мост, Уэйтсфилд, ВТ.
Консервативный подход к этой ситуации состоит в том, чтобы пренебречь влияние валика и продолжите анализ, как если бы подпорки не было. Однако в некоторых случаях такой анализ может свидетельствовать о необходимости усиления или замены элементов фермы. В В этом случае, возможно, целесообразно дополнительно рассмотреть возможность пользу этого элемента. Каждая установка этого типа элемента будут уникальными, и общие практические правила недоступны.
Расчет систем перекрытий, как правило, проще, чем для ферм системы, но результаты все равно могут быть разочаровывающими, потому что результаты часто указывают на то, что компоненты пола могут быть перенапряжены, когда они способны выдерживать ежедневную нагрузку без видимое бедствие. Поскольку крытые мосты поставляются с рядом конфигурации напольной системы, в следующих разделах обсуждаются отдельные компоненты более распространенных конфигураций, найденных в самые крытые мосты.
Балки перекрытий
Поперечные балки перекрытий, соединяющие продольные фермы, являются основными элементами, участвующими в поддержке транспортного средства нагрузки и передачи динамических нагрузок на эти фермы. инициал дилемма в их анализе заключается в установлении длины пролета для балка пола. Для тех балок перекрытий, которые опираются на ферму конфигурация с несколькими хордами, можно выбрать самую короткую расстояние между самыми внутренними поясами и минимизировать напряжения изгиба в балке перекрытия или выберите максимальное расстояние между крайними хорды и будьте осторожны с напряжениями балки перекрытия. Некоторые аналитики постарайтесь установить разумную длину подшипника на каждой опоре и используйте центры этих несущих областей, чтобы задать пролет балки перекрытия. Хотя это разумно, оно в значительной степени зависит от точного опорные поверхности на балках и идеально ровных поверхностях и плоские на вершинах нижних поясов фермы. Всегда есть исключения из любого правила, но хорошим обобщением является использование расстояние между центрами ферм как теоретическое длина поддерживаемого пролета для балки перекрытия. Начиная с этого предположения, результаты могут быть оценены позже для их чувствительность к скромным теоретическим изменениям в поддержке расположение.
Следующая проблема при оценке балок перекрытий связана с распределение осей нагрузки на эти балки (обратите внимание, силы нагрузки и сопутствующие напряжения редко бывают значительными в традиционные мосты). Спецификации AASHTO предлагают конкретные рекомендации по продольному коэффициенту распределения нагрузки в зависимости от от типа палубной системы, пролетающей между балками перекрытий. Стол 3.23.3.1 «Распределение колесных нагрузок в поперечных балках» (ААШТО Стандартные спецификации ), обеспечивает ряд значения от S/4 для обычной системы продольных палубных досок до S/5 для мостовидного протеза с накладками из гвоздей или клея, 150 мм (6 дюймов) или более толщиной ^[2] .
Поскольку результаты могут быть переменными, это распределение нагрузки значение было предметом интенсивных дебатов среди инженеров-мостостроителей. в течение длительного периода, и исследования по этой теме продолжаются. Ан аналитическая оценка любой балки перекрытия может означать, что ее грузоподъемность — определенное количество тонн, хотя балка перекрытия имеет успешно поддерживает транспортные средства с нагрузкой на ось значительно большие суммы в течение длительного времени. точность коэффициентов распределения нагрузки AASHTO составляет всего один способствует разрыву между теоретическим анализом и реальным опыт.
Специалисты по крытым мостам должны знать о проблеме факторов распределения и рекомендуется держать в курсе любых будущие улучшения рекомендаций AASHTO по нагрузке на ось для поперечные балки перекрытий.
В стальных или бетонных балках перекрытий изгибающие напряжения часто контролируют допустимая допустимая постоянная нагрузка сверх тех пределов, которые возникают при сдвиге напряжения, но сдвиг является важной проблемой в любой конструкции из дерева и следует проверить. Напомним, что спецификации древесины NDS (как обсуждается в разделе «Поперечное усилие» в Главе 3 NDS), позволяют аналитик, чтобы пренебречь любыми сосредоточенными нагрузками (колесами), которые расположены в пределах глубины балки опоры балки. Загружается близко к можно предположить, что опоры проходят непосредственно через жесткие опоры, не вызывая поперечных касательных напряжений. Подраздел 13.6.5.2, «Фактическое напряжение», в AASHTO Стандарт Спецификации автомобильных мостов позволяют пренебрегают, если в пределах трехкратной глубины луч. ^[2] Это важное отличие для тех, связаны с крытыми мостами.
Строители часто делали надрезы на нижней стороне этих балок перекрытий в опора балки для вставки балок или выравнивания верхних поверхностей слегка меняющиеся балки для поддержки их на слегка неровных поверхностях. Также была уменьшена форма верхних углов некоторых балок перекрытий, особенно те, которые проникли в веб-компоненты города решетчатая ферма. Спецификации NDS содержат рекомендации по обработка надрезов на нижней поверхности, так как они связаны с уменьшением дееспособность членов. Коэффициент напряжения сдвига NDS функционально наказывает за надрез-удаление половины луча учетверяет, а не удваивает напряжение сдвига. это просто способ учета концентрации касательных напряжений в углах выемки. NDS ограничивает глубину любой нижней выемки до четверть толщины луча. Касательные напряжения в балках перекрытий с верхом угловые сокращения и высшие метки могут быть проанализированы с помощью традиционное использование механики материалов. Британский лесной кодекс также предлагает некоторые рекомендации по максимально допустимому верхнему надрезу и рекомендует конусы; эти темы рассматриваются очень легко в Американские рекомендации по проектированию деревянных конструкций.
Ни спецификации NDS, ни большинство других традиционных справочники содержат много указаний по армированию пола балки, подвергшиеся значительным надрезам и которые, поэтому проявляют сопутствующие высокие напряжения сдвига. Немного современные книги по деревянному строительству упоминают вертикальный через болты и боковые пластины. Другое решение состоит в том, чтобы просто использовать более крупный балка пола. Усиление области надреза может быть гораздо более экономичное решение. Однако надлежащие методы и аналитические проблемы в этих схемах армирования в торцевых вырезах не получили широкого распространения. обнародовано. ^[7]
Теоретическая несущая способность поперечных балок перекрытий регулярно ниже, чем их способность к изгибу, но разрушения при сдвиге в балках перекрытий встречаются редко. Отсюда, как и в случае со спором включая соответствующий коэффициент распределения нагрузки на балку перекрытия анализ, оценка прочности на сдвиг в тяжелых деревянных балках перекрытий обсуждают уже много лет. Приложение в NDS Спецификации описывают двухлучевую теорию того, почему деревянные балки которые разделились на два отдельных члена, могут продолжать нести значительная нагрузка. ^[3] Сноски к дополнению к NDS из допустимых напряжений отмечают, что касательное напряжение увеличивается с надежно меньшая проверка — в два раза больше табличных значений без проверки. Это отражает тот факт, что касательное напряжение был сокращен больше, чем любой другой тип стресса за последнее столетие. Это в первую очередь отражает влияние камерной сушки на размеры пиломатериалы. Относительно тонкие элементы при воздействии некоторых иногда суровые режимы печи, склонны к большим расколам или чеки на концах, где древесина сохнет быстрее всего. Эти конечные проверки совпадают с наиболее типичным местом для максимальных касательных напряжений в простых балках с равномерным нагружением. Просто уменьшить допустимое напряжения сдвига, чтобы покрыть эти несчастные повреждения печи, не существенно влияет на размерную конструкцию пиломатериала, но может быть имеет большое значение в более тяжелых деревянных конструкциях. Разумно утверждают, что большие, выдержанные бревна с вертикальными сердцевинами, если любые, можно предположить, что они имеют минимальные проверки на концах. Аналитики должны быть довольны принятием этого допустимого увеличения касательные напряжения. Однако спецификации AASHTO и NDS не все же уточненные текущие руководящие принципы. Исследования продолжаются в этом область.
Еще одна проблема, заслуживающая особого внимания в отношении балок перекрытий. прогибы временной нагрузки. Спецификации AASHTO указывают ограничения прогиба элементов деревянного пола в подразделе 13.4, «Отклонение.»h ^[2] Во многих случаях теоретическое оценка прогиба динамической нагрузки покажет, что балка перекрытия может иметь достаточную прочность на сдвиг и изгиб, чтобы удовлетворять текущим требованиям спецификации, но не будет удовлетворять текущему прогибу методические рекомендации. Хотя этот вопрос прогиба не получил много внимание в современной литературе, это обычная ситуация и один что требует вдумчивого рассмотрения.
Распределительные балки
Как упоминалось ранее в главе 5 настоящего руководства, некоторые системы полов моста были оснащены лонжеронами подвешены под поперечными балками перекрытия и соединены с ними. Эти в данном руководстве элементы обозначены как распределительные балки, потому что они добавляются, чтобы сделать пол жестче и укрепить его за счет уменьшения нагрузка на любую одиночную балку перекрытия. Они делают это, увеличивая тенденция распределять точечную нагрузку в продольном направлении, среди более лучи. Общее соединение между распределительными и перекрытиями представляет собой тяжелый U-образный болт для прижатия распределительной балки к днищу балок перекрытия с U-образным болтом на каждой второй балке перекрытия. Следовательно, когда ось автомобиля пересекает мост, она отклоняет балку пола который, в свою очередь, толкает распределительную балку вниз, тем самым вытягивая соседние балки перекрытий вниз таким образом, чтобы распределить нагрузку на более чем одна балка перекрытия. Это своего рода тяжелые подвесные стрингеры. Распределительные балки часто строятся из нескольких части вертикальных планок. Это упростило установку, а позволяя установщику расположить отдельные стыковые соединения в шахматном порядке сделать распределительный пучок достаточно равномерным по всей длине пролет моста. Рисунок 96 показан пример распределительной балки системы (обратитесь к рисунку 45 для другого примера).
Рис. 96. Распределительная балка Worral’s Бридж, Рокингем, штат Вирджиния.
Надлежащий аналитический анализ этой довольно сложной системы пола является сложной задачей и может быть разочаровывающим. Нужно тщательно моделировать соединение между балкой перекрытия и распределительной балкой, чтобы обеспечить правильное отношение, когда во многих случаях установка расшатываются из-за усадки или износа древесины. Свободное соединение может значительно снизить теоретическую мощность предполагаемого помощник. Эта система наложения сетки с ее поперечной нагрузкой, кажется, заслуживает компьютерного анализа для оценки распределения нагрузки между разные элементы. Это имеет смысл только тогда, когда система пола с опорными продольными фермами. Тяжелые фермы меньше, чем абсолютно жесткие под динамической нагрузкой и их прогибы еще больше усложняют поведение системы решетчатого пола. Этот явление довольно обычное, когда аналитики сталкиваются со своими первыми тяжелыми деревянный ферменный мост. Компоненты взаимодействуют до такой степени, и настолько сложными способами, что компьютерная модель может очень быстро становятся слишком большими и сложными для разумного анализа.
Спецификации AASHTO не относятся к этим дистрибутивам. лучи. Оценка распределительных балок, установленных на 24 мостах было проведено в рамках общегосударственного исследования 75 крытых мостов в Вермонт. Это исследование пришло к выводу, что следует пренебрегать любым потенциальным преимущества распределительных балок из-за часто наблюдаемого неплотное соединение с балками перекрытий.
Хотя соединения слишком слабы для распределения балки, чтобы предложить очевидную пользу для моста, эти соединения по-прежнему способны удерживать распределительные балки и, таким образом, налагают штраф за статическую нагрузку на несущую способность балки перекрытия. Потенциальное преимущество подвешенного статического груза, помогающего демпфировать вибрации в системе пола достаточно эзотеричны, чтобы бросить вызов многим дальнейший анализ. Соответственно, отчет Вермонта, наконец, рекомендуется снять распределительные балки во время строительства моста. следующая реабилитация. Кроме того, модификации деталей подключения не были достаточно надежными, чтобы рекомендовать их сохранение. Окончательно, потому что большинство этих членов были добавлены во время середина 20 ^-й-й век, они не имеют существенного исторического важности, поэтому их удаление не должно касаться исторических защитники.
Исходя из этого обсуждения, распределительные балки не рекомендуются для новых крытых мостов или при восстановлении существующих крытых мосты. Далее их следует снимать с мостов во время последующие реабилитационные проекты.
Стрингеры
Анализ является относительно обычным для систем настила пола, которые включают слой продольных стрингеров. Длина поддержки обычно принимается за межцентровое расстояние между несущие поперечные балки перекрытия. Руководство по динамической нагрузке распределяется по отдельным стрингерам, предоставляется AASHTO в Таблица 3. 23.1, «Распределение колесных нагрузок в продольных балках» из Стандартные спецификации . ^[2] Эта нагрузка коэффициент распределения зависит от толщины и состава материала настила между стрингерами. Пока там является свидетельством того, что коэффициенты распределения AASHTO для таких стрингеров также консервативны, стрингеры в аутентичных крытых мостах часто имеют большую теоретическую грузоподъемность, чем опорный пол лучи.
Хотя изгибающие напряжения традиционно контролируют способность стрингеры, напряжения сдвига также должны быть проверены. Как и в случае с поперечная балка перекрытия, спецификации NDS позволяют провести анализ для сдвига, чтобы пренебречь любой динамической нагрузкой в пределах теоретической глубины стрингера от опоры, а спецификации AASHTO позволяют пренебрегать грузами транспортных средств в пределах трехкратной глубины стрингер.
Настил
Очень широкий выбор конфигураций деревянного настила, крытые мосты затрудняют обобщение этой темы, хотя несколько типов настилов достаточно распространены, чтобы упомянуть конкретно. Продольный настил, проходящий между поперечными балки перекрытий могут быть плоскими и очень тяжелыми дощатыми конструкциями, доски с ламинированным гвоздем по краю или панели из клееного бруса. ААШТО спецификации обеспечивают руководство по этому распределению нагрузки и опорных пролетов в этих типах настила в подразделе 3.25, «Распределение колесных нагрузок на деревянный настил». ^[2] Проблемы, связанные как с изгибными, так и с сдвиговыми напряжениями, аналогичны те, которые обсуждались выше для стрингеров и пола лучи.
Еще одной сложностью при оценке деревянного настила является довольно распространенные жертвенные беговые доски поверх основных настил. Хотя спецификации AASHTO не предлагают никаких руководство относительно воздействия этих досок, рекомендуется что структурный вклад этих обычно легких досок пренебрегать при анализе системы пола.
Анализ растяжек мало описан в текстах. Больше всего бодрит установлен в крытых мостах, чтобы помочь сохранить структуру выровненной и для противодействия силам, которые могут перестроить участников. Главным сила, уводящая мост от прямой и отвесной, является боковой ветровая нагрузка.
Многие классические и базовые тексты по проектированию строительных конструкций обсуждают анализ силы в системах ветровой жесткости, используемых в стали через фермы. ^[14,15] Для основного однопролетного строения, горизонтальная ветровая нагрузка делится поровну между нагрузкой против верхний пояс и нагрузка на нижний пояс. Ветровые нагрузки применяемые на уровне нижнего аккорда, передаются напрямую и продольно к упорам, через нижнюю боковую систему (или сама дека, как диафрагма). Большинство напольных палуб могут обеспечить достаточная боковая нагрузка без дополнительной системы крепления, при условии, что есть хорошие соединения с фермой. Ветер однако нагрузка, приложенная к верхнему уровню пояса, также должна путешествовать назад и вниз к абатментам с помощью некоторых средств, которые часто бывают не очень прочными и жесткими.
Существует два способа определения приложенных ветровых нагрузок верхнего уровня. перенесены наружу и вниз к абатментам. Разница в основном в том, передаются ли боковые нагрузки вниз на уровень палубы а затем к абатментам, или они переносятся на на верхний уровень, а затем сразу вниз, либо на устои или портал. Первый вариант анализа – оценка ветра нагрузка на уровне верхнего пояса, собирающаяся к концам пролет, а затем передается вниз к опорам через очень тяжелое портальное обрамление. Боковая нагрузка накапливается вдоль пролет, сильно нагружающий торцевые панели подвесной Х-системы. Много существующие системы крепления верхнего уровня могут нести нагрузки на мост заканчивается, но достаточно лишь очень редкого портала хорошо детализированы и усилены, чтобы справиться с этой концентрированной вертикальной перенос нагрузки. Чтобы этот несущий механизм работал как по назначению, система концевой качающейся рамы должна быть особенно хорошо связаны и детализированы. В зависимости от деталей подключения используемых для этого типа системы, силы расчалки можно рассматривать быть только растяжением-сжатием или только сжатием, что еще больше усложняет конструкция этой очень тяжелой схемы обрамления портала.
Другим вариантом анализа является оценка ветровой нагрузки применяется на уровне верхнего аккорда как переносимый немедленно до уровня настила на каждой промежуточной качающейся раме или ферме вертикально в точках панели. Это позволяет избежать создания большого и сосредоточенная боковая сила на концах моста. Этот сценарий создает меньшую силу на любой заданной раме качания, которая требует меньше каждого из них, но одни и те же проблемы преобладают в отношении растяжения-сжатия или только компрессионные суставные детали в брекетах.
Принимая во внимание эти две совершенно разные схемы поперечного распределения нагрузки, размеры распорок, соединения, интервалы и детали сильно различаются в зависимости от исторические крытые мосты. В большинстве случаев крепление существующий мост можно обосновать аналитически, и тем самым улучшения могут не понадобиться. Но в других случаях улучшения может быть указано как совершенно необходимое из-за неадекватного размеры и/или детали.

Материал для навесов прозрачный: Зачем нужна прозрачная крыша и 5 лучших материалов для нее

Программа для создания интерьера мансарды с наклонными стенами: Программа для дизайна интерьера квартиры и дома

2 сентября, 2020 alexxlab

Как сделать правильно обрешетку: Как сделать обрешетку крыши своими руками

Содержание Обрешетка под сайдинг: пошаговая инструкцияОбрешетка под сайдинг из дерева своими рукамиМеталлическая обрешетка под сайдинг из металлопрофиляОбрешетка для цокольного сайдингаМонтаж обрешетки под виниловый сайдинг на утеплитель пенополистиролКак сделать обрешетку фронтона под сайдингМонтаж обрешетки вокруг окон и дверей под сайдингНужна ли обрешетка на ОСБ под сайдинг каркасного домаВидео о том, как сделать обрешетку под сайдинг (пошаговая […]

Читать далее

20 мая, 1978 alexxlab

Хромовый цвет фото: Цвет Ral 6020 Хромовый зелёный в каталоге цветовой палитры

Содержание какой это оттенок, с какими красками сочетать в дизайнеЦвет хром — что под этим понимается, как выглядитМатовые и глянцевые оттенки хромированного цвета, как сочетать с другими цветамиПрименение хромированного эффекта в дизайнеГостинаяСпальняКухняВаннаяПрихожаяОсобенности применения в интерьереМебельДвериШторы, текстиль и другой декорИспользование при отделке помещенийПотолок, пол и стеныПримеры интерьеров с хромированными элементамиВидео: Декоративное хромированиеХромированные диски — основные методы […]

Читать далее

6 марта, 2020 alexxlab

Краска по металлу жаростойкая – какую жаростойкую краску выбрать для печки из металла, высокотемпературная, жаропрочная, чем покрасить металлическую печь

Содержание какую жаростойкую краску выбрать для печки из металла, высокотемпературная, жаропрочная, чем покрасить металлическую печьВыбираем краску для печиНемного о разновидностях жаростойких красокКак правильно выбратьРасцветкаРасфасовкаКакую огнеупорную краску выбрать для печиПодготавливаем поверхность для покраскиСамодельная огнеупорная краскаВыбираем краску для кирпичной печи в банеТермостойкая краска по металлу для печей — обзор огнеупорной, жаростойкой эмали, рекомендации по выборуТоп-5 термостойких красок […]

Читать далее

Расчет плоских ферм: Расчет ферм с примерами решения и образцами выполнения

Расчет плоских ферм: Расчет ферм с примерами решения и образцами выполнения

Расчет ферм с примерами решения и образцами выполнения

Расчет плоских ферм

Расчет ферм

Error

Расчет ветровой нагрузки на ферму крыши согласно IS 875-2015

Débouchage canalisation Montpellier-SOS-Débouchage 34

ENTREPRISE DÉBOUCHAGE MONTPELLIER

ТАРИФЫ DEBOUCHAGE CANALISATION MONTPELLIER

PLOMBIER DEBOUCHAGE CANALISATION MONTPELLIER

SOS DÉBOUCHAGE MONTPELLIER

Plombier d’urgence 24h/24 et 7 jours/7 sur Montpellier

Entreprise de debouchage canalisations Montpellier

Débouchage Montpellier

SOS Débouchage Montpellier

ВИДЕОКАНАЛИЗАЦИЯ ИНСПЕКЦИИ

Упрощенный анализ ферм

Уточненный анализ фермы

Комбинированная ферма и арка Анализ

Влияние балочных балок

Балки перекрытий

Распределительные балки

Стрингеры

Настил

Previous Post

Материал для навесов прозрачный: Зачем нужна прозрачная крыша и 5 лучших материалов для нее

Next Post

Программа для создания интерьера мансарды с наклонными стенами: Программа для дизайна интерьера квартиры и дома

Добавить комментарий Отменить ответ

Расчет плоских ферм: Расчет ферм с примерами решения и образцами выполнения

Расчет плоских ферм: Расчет ферм с примерами решения и образцами выполнения

Расчет ферм с примерами решения и образцами выполнения

Расчет плоских ферм

Расчет ферм

Error

Расчет ветровой нагрузки на ферму крыши согласно IS 875-2015

Débouchage canalisation Montpellier-SOS-Débouchage 34

ENTREPRISE DÉBOUCHAGE MONTPELLIER

ТАРИФЫ DEBOUCHAGE CANALISATION MONTPELLIER

PLOMBIER DEBOUCHAGE CANALISATION MONTPELLIER

SOS DÉBOUCHAGE MONTPELLIER

Plombier d’urgence 24h/24 et 7 jours/7 sur Montpellier

Entreprise de debouchage canalisations Montpellier

Débouchage Montpellier

SOS Débouchage Montpellier

ВИДЕОКАНАЛИЗАЦИЯ ИНСПЕКЦИИ

Упрощенный анализ ферм

Уточненный анализ фермы

Комбинированная ферма и арка Анализ

Влияние балочных балок

Балки перекрытий

Распределительные балки

Стрингеры

Настил

Previous Post

Материал для навесов прозрачный: Зачем нужна прозрачная крыша и 5 лучших материалов для нее

Next Post

Программа для создания интерьера мансарды с наклонными стенами: Программа для дизайна интерьера квартиры и дома

Related Articles

Как сделать правильно обрешетку: Как сделать обрешетку крыши своими руками

Хромовый цвет фото: Цвет Ral 6020 Хромовый зелёный в каталоге цветовой палитры

Краска по металлу жаростойкая – какую жаростойкую краску выбрать для печки из металла, высокотемпературная, жаропрочная, чем покрасить металлическую печь

Добавить комментарий Отменить ответ