Расчет элементов: Калькулятор расчета алиментов онлайн 2020

В 1869 г. Д. И. Менделеев вывел периодический закон, доказывающий периодическую зависимость свойств элементов от заряда атомного ядра. Ученый создал периодическую систему химических элементов, представив ее в виде таблицы, в которой разместил химические элементы по мере возрастания атомной массы. Стоит заметить, что химические элементы в современной таблице расположены по возрастанию числа протонов в ядре атома, что отображает атомный номер элемента. В таблице он записан над символом элемента, его атомная масса записана под символом. Атомная масса химических элементов может быть нецелым числом, т.к. это средневзвешенная величина от всего количества изотопов элемента, имеющихся в природе. Таблица состоит из групп, периодов и рядов. Горизонтальные строки таблицы — периоды (от 1 до 7), вертикальные столбцы называются группами, обозначаются римскими цифрами (0 и дальше от I до VIII) и буквами (А, Б). Римский номер столбца обозначает количество валентных электронов у элементов данной группы. Каждая группа, кроме 0 и VIII, делятся на главную и под главную подгруппы. В главных с увеличением порядкового номера возрастают и металлические свойства элементов. В начале каждого периода, кроме первого, стоит элемент с сильно выраженными металлическими свойствами. С увеличением порядкового номера, равного положительному заряду ядра его атома, нарастают неметаллические свойства, а металлические — ослабевают. Предпоследний элемент периода имеет сильно выраженные неметаллические свойства (галоген), последним элементом является инертный газ. Каждый период имеет не одинаковое количество элементов, если в I-м периоде их 2, то во II-м и III-м по 8 элементов в каждом, следующие два IV и V периоды имеют по 18 элементов, VI — 32, а VII — 17. Последний период является не завершенным. Три первых, малых, периода имеют 1 горизонтальный ряд, остальные, большие периоды имеют по 2 горизонтальных ряда каждый — четный и нечетный. 14 элементов, имеющих сходные с лантаном (порядковый номер 53) химические свойства, выделены под основной таблицей. Представлены в отдельной таблице и элементы, схожие с актинием.

Чтобы рассчитать параметры химического элемента из периодической таблицы, воспользуйтесь онлайн калькулятором.

Калькулятор расчета параметров химических элементов из таблицы Менделеева

Расчет элементов конструкций цельного сечения

Элементами деревянных конструкций называют доски, бруски, брусья и бревна цельного сечения с размерами, указанными в сортаментах пилёных и круглых материалов. Они могут являться самостоятельными конструкциями, например, балками или стойками, а также стержнями более сложных конструкций. Усилия в элементах определяют общими методами строительной механики. Проверка прочности и прогибов элемента заключается в определении напряжений в сечениях, которые не должны превышать расчетных сопротивлений древесины, а также его прогибов, которые не должны превосходить предельных, установленных нормами проектирования. Деревянные элементы рассчитывают в соответствии со СНиП II-25-80.

Растянутые элементы

На растяжение работают нижние пояса и отдельные раскосы ферм, затяжки арок и других сквозных конструкций. Растягивающее усилиеN действует вдоль оси элемента и во всех точках его поперечного сечения возникают растягивающие напряжения σ, которые с достаточной точностью считаются одинаковыми по величине.

Древесина на растяжение работает почти упруго и показывает высокую прочность. Разрушение происходит хрупко в виде почти мгновенного разрыва. Стандартные образцы при испытаниях на растяжение имеют вид «восьмерки».

Как видно из диаграммы растяжения древесины без пороков, зависимость деформаций от напряжений близка к линейной, а прочность достигает 100 МПа.

Однако прочность реальной древесины при растяжении, учитывая ее значительные колебания, большое влияние пороков и длительности нагружения значительно ниже: для неклееной древесины I сорта R_р=10 МПа, для клееной древесины влияние пороков уменьшается, поэтому R_р=12 МПа. Прочность растянутых элементов в тех местах, где есть ослабления снижается в результате концентрации напряжений у их краев, т.е. вводится коэффициент условия работы m₀=0,8. Тогда получается расчетное сопротивление R_р=8 МПа. Проверочный расчет растянутых элементов производится по формуле:

σ, где

–площадь рассматриваемого поперечного сечения, причем ослабления, расположенные на участке длиной 20 см. считаются совмещенными в одном сечении. Для подбора сечений пользуются этой же формулой, но относительно искомой (требуемой) площади .

Сжатые элементы

На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм. В сечениях элемента от сжимающего усилияN, действующего вдоль его оси, возникают почти одинаковые по величине сжимающие напряжения σ (эпюра прямоуголная).

Стандартные образцы при испытании на сжатие имеют вид прямоугольной призмы с размерами, указанными на рис. 2.

Древесина работает на сжатие надежно, но не вполне упруго. Примерно до половины предела прочности рост деформаций происходит по закону близкому к линейному, и древесина работает почти упруго. При росте нагрузки увеличение деформаций все более опережает рост напряжений, указывая на упруго-пластический характер работы древесины.

Разрушение образцов без пороков происходит при напряжениях, достигающих 44 МПа, пластично, в результате потери устойчивости ряда волокон, о чем свидетельствует характерная складка. Пороки меньше снижают прочность древесины, чем при растяжении, поэтому расчетное сопротивление реальной древесины при сжатии выше и составляет для древесины 1 сорта R_с=14÷16 МПа, а для 2 и 3 сортов эта величина немного ниже.

Расчет на прочность сжатых элементов производится по формуле:

σ, где

R_с – расчетное сопротивление сжатию.

Аналогичным образом рассчитываются и сминаемые по всей поверхности элементы. Сжатые стержни, имеющие большую длину и не закрепленные в поперечном направлении должны быть, помимо расчета на прочность, рассчитаны на продольный изгиб. Явление продольного изгиба заключается в том, что гибкий центрально-сжатый прямой стержень теряет свою прямолинейную форму (теряет устойчивость) и начинает выпучиваться при напряжениях, значительно меньших предела прочности. Проверку сжатого элемента с учетом его устойчивости производят по формуле:

σ, где

–расчетная площадь поперечного сечения,

φ – коэффициент продольного изгиба.

принимается равной:

1. При отсутствии ослаблений =,

2. При ослаблениях, не выходящих на кромки, если площадь ослаблений не превышает 25% , =,

3. То же, если площадь ослаблений превышает 20% , =4/3,

1. При симметричных ослаблениях, выходящих на кромки =,

При несимметричном ослаблении, выходящем на кромки, элементы рассчитывают как внецентренно сжатые.

Коэффициент продольного изгиба φ всегда меньше 1, учитывает влияние устойчивости на снижение несущей способности сжатого элемента в зависимости от его расчетной максимальной гибкости λ.

Гибкость элемента равна отношению расчетной длины l₀ к радиусу инерции сечения элемента:

; .

Расчетную длину элемента l₀ следует определять умножением его свободной длины l на коэффициент μ₀:

l₀=l μ₀, где

коэффициент μ₀ принимается в зависимости от типа закрепления концов элемента:

— при шарнирно закрепленных концах μ₀=1;

— при одном шарнирно закрепленном, а другом защемленном μ₀=0,8;

— при одном защемленном, а другом свободном нагруженном конце μ₀=2,2;

— при обоих защемленных концах μ₀=0,65.

Гибкость сжатых элементов ограничивается с тем, чтобы они не получились недопустимо гибкими и недостаточно надежными. Отдельные элементы конструкций (отдельные стойки, пояса, опорные раскосы ферм и т.п.) должны иметь гибкость не более 120. Прочие сжатые элементы основных конструкций – не более 150, элементы связей – 200.

При гибкости более 70 (λ>70) сжатый элемент теряет устойчивость, когда напряжения сжатия в древесине еще невелики и она работает упруго.

Коэффициент продольного изгиба (или коэффициент устойчивости), равный отношению напряжения в момент потери устойчивости σ_кр к пределу прочности при сжатии R_пр, определяют по формуле Эйлера с учетом постоянного отношения модуля упругости древесины к пределу прочности:

, где

А=3000 – для древесины,

А=2500 – для фанеры.

При гибкостях, равных и меньших 70 (λ≤70) элемент теряет устойчивость, когда напряжения сжатия достигают упругопластической стадии и модуль упругости древесины понижается. Коэффициент продольного изгиба при этом определяют с учетом переменного модуля упругости по упрощенной теоретической формуле:

, где

=0,8 – коэффициент для древесины;

=1 – коэффициент для фанеры.

При подборе сечения используют формулу расчета на устойчивость, предварительно задаваясь величиной λ и φ.

Изгибаемые элементы

В изгибаемых элементах от нагрузок, действующих поперек продольной оси, возникают изгибающие моменты М и поперечные силы Q, определяемые методами строительной механики. Например, в однопролетной балке пролетом l от равномерно-распределенной нагрузки q возникают изгибающие моменты и поперечные силы .

От изгибающего момента в сечениях элемента возникают деформации и напряжения изгиба σ, которые состоят из сжатия в одной части сечения и растяжения в другой, в результате элемент изгибается.

Диаграмма как и для сжатия, примерно до половины, имеет линейное очертание, затем изгибается, показывая ускоренный рост прогибов.

=80 МПа – предел прочности чистой древесины на изгиб при кратковременных испытаниях. Разрушение образца начинается с появления складок в крайних сжатых волокнах и завершается разрывом крайних растянутых. Расчетное сопротивление изгибу по СНиП II-25-80 рекомендуется принимать таким же, как и при сжатии, т.е. для 1 сорта R_и=14 МПа – для элементов прямоугольного сечения высотой до 50 см. Брусья с размерами сечения 11 – 13 см. при высоте сечения 11 – 50 см. имеют меньше перерезанных волокон при распиловке, чем доски, поэтому их прочность повышается до R_и=15 МПа. Бревна шириной свыше13 см. при высоте сечения 13 – 50 см. совсем не имеют перерезанных волокон, поэтому R_и=16 МПа.

Расчет прочности по нормальным сечениям элементов прямоугольного профиля (три типа задач)

12 мая 2016 г.

Изгибу подвергаются железобетонные плиты и балки, которые могут быть как самостоятельными конструкциями, так и входить в состав сложных конструкций и сооружений (ребристые плиты, подпорные стены, рыбо-, судопропускные шлюзы, перегораживающие сооружения и др.). При одиночном армировании рабочая арматура расположена только в растянутой зоне. 

Расчет по прочности нормальных сечений к продольной оси элементов прямоугольного сечения сводится к решению следую­щих задач: 

1. подбор такого поперечного сечения, которое соответствует тре­буемой прочности, т.е. определение требуемой площади сече­ния растянутой арматуры при заданных внешних усилиях, клас­сах бетона и стали, предварительно назначенных размерах се­чения элемента; 
2. определение требуемой площади сечения растянутой арматуры и недостающего размера сечения элемента при заданных вне­шних усилиях, классах бетона и арматуры, предварительно на­значенных проценте армирования сечения и одном из размеров поперечного сечения элемента; 
3. проверка прочности заданного сечения элемента, заключающа­яся в сопоставлении заданного внешнего изгибающего момен­та с внутренним, соответствующим предельному состоянию рас­сматриваемого сечения элемента. 

Рассмотрим изгибаемый элемент прямоугольного поперечного сечения с одиночной арматурой (рис. ниже) в момент, когда в растя­нутой и сжатой зонах сечения, проходящего через трещину, одно­временно наступает предельное состояние.  

К расчету изгибаемых элементов с одиночным армированием

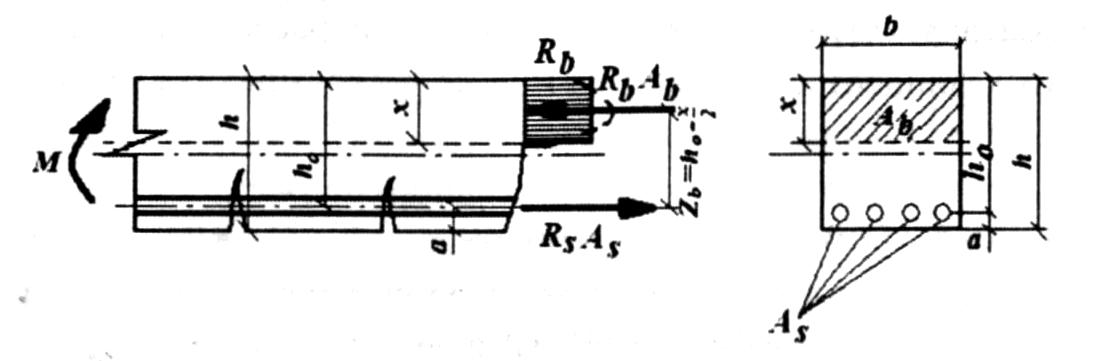
Чтобы составить условие прочности нормального сечения, от­делим часть балки и покажем внутренние усилия, обеспечивающие равновесие этой части балки.

В сжатой зоне бетона

R_bA_b = R_bbx

а в растянутой зоне

R_sA_s = R_s1A_s1 + R_s2A_s2 +…+R_snA_sn

Плечо этих сил Z_b = h₀— 0,5х.

В расчетном предельном состоянии при разрушении элемента по случаю 1, составляются 2 условия прочности: относительно цен­тра тяжести растянутой арматуры

M ≤ M_b = R_bbx(h_o-0,5x)

или относительно центра тяжести сжатой зоны бетона

M ≤ M_s = R_sA_s(h_o-0,5x)

Из этих уравнений очевидно, что М_b=M_s т. е. предельные внут­ренние усилия в обеих зонах сечения одинаковы:

R_bbx = R_sA_s

Основные уравнения прочности прямоугольных сечений изги­баемых элементов выше, справедливы при высоте сжатой зоны х меньше граничной высоты x_R, т. е. когда соблюдается усло­вие x ≤ h₀ ξ_R

Условие выше справедливо только при ξ = х / h₀ ≤ ξ_R , где ξ_R — граничное значение относительной высоты сжатой зоны, вычисля­ется по формуле

В зависимости  w = α — 0,008R_b — характеристика сжатой зоны бетона.

Коэффициент:

α = 0,85 — для тяжелого бетона;

α = 0,8 — для легкого и поризованного бетона;

α = 0,75-0,8 — для мелкозернистого.

Напряжения в арматуре σ_sr принимаются в зависимости от класса арматуры. Напряжения σ_sr u = 500 МПа при γ_b2 < 1 и σ_sr u = 400 МПа при γ_b2 ≥ 1.

При решении задачи 1-го типа из уравнения выше определяют высоту сжатой зоны

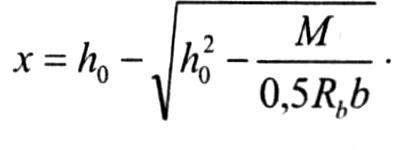
Подставляя полученное значение «x» в формулу выше, вычис­ляют площадь A_s (сечения арматуры растянутой зоны)

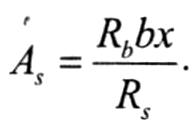
По полученной величине A_s по сортаменту подбирают количе­ство стержней, их диаметр и размещают арматуру в растянутой зоне сечения.

При решении задач 2-го типа определяют относительную вы­соту сжатой зоны бетона

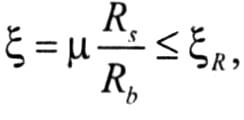
по таблице ниже находят коэффициент φ =А₀ = α_m и вычисляют полез­ную (рабочую) высоту h₀

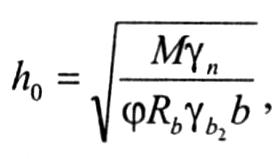
а дальше ведут расчет по 1 типу. Граничную относительную высоту сжатой зоны ξ_R определяют по формуле выше или по таблице ниже.

Коэффициенты для расчета железобетонных изгибаемых элементов прямоугольного сечения 

ξ (θ)	ζ (δ)	А0 (αm)	ξ (θ)	ζ (δ)	А0 (αm)
0,01	0,995	0,010	0,36	0,820	0,295
0,02	0,990	0,020	0,37	0,815	0,301
0,03	0,985	0,030	0,38	0,810	0,308
0,04	0,980	0,039	0,39	0,805	0,314
0,05	0,975	0,048	0,40	0,800	0,320
0,06	0,970	0,058	0,41	0,795	0,326
0,07	0,965	0,067	0,42	0,790	0,332
0,08	0,960	0,077	0,43	0,785	0,337
0,09	0,955	0,085	0,44	0,780	0,343
0,10	0,950	0,095	0,45	0,775	0,349
0,11	0,945	0,104	. 0,46	0,770	0,354
0,12	0,940	0,113	0,47	0,765	0,359
0,13	0,935	0,121	0,48	0,760	0,365
0,14	0,930	0,130	0,49	0,755	0,370
0,15	0,925	0,139	0,50	0,750	0,375
0,16	0,920	0,147	0,51	0,745	0,380
0,17	0,915	0,155	0,52	0,740	0,385
0,18	0,910	0,164	0,53	0,735	0,390
0,19	0,905	0,172	0,54	0,730	0,394
0,20	0,900	0,180	0,55	0,725	0,399
0,21	0,895	0,188	0,56	0,720	0,403
0,22	0,890	0,196	0,57	0,715	0,408
0,23	0,885	0,203	0,58	0,710	0,412
0,24	0,880	0,211	0,59	0,705	0,416
0,25	0,875	0,219	0,60	0,700	0,420
0,26	0,870	0,226	0,61	0,695	0,424
0,27	0,865	0,233	0,62	0,690	0,428
0,28	0,860	0,241	0,63	0,685	0,432
0,29	0,855	0,248	0,64	0,680	0,435
0,30	0,850	0,255	0,65	0,675	0,439
0,31	0,845	0,262	0,66	0,670	0,442
0,32	0,840	0,269	0,67	0,665	0,446
0,33	0,835	0,275	0,68	0,660	0,449
0,34	0,830	0,282	0,69	0,655	0,452
0,35	0,825	0,289	0,70	0,650	0,455

Значения граничной относительной высоты сжатой зоны нормального сечения

Класс арматуры	А240	А300	А400	А500	В500
ξR	0,612	0,577	0,531	0,493	0,502

Решение задачи 3-го типа сводится к определению:

• величины сжатой зоны бетона

x = R_sA_sγ_s / R_bbγ_b2

• изгибающего момента, воспринимаемого сжатой зоной бетона

M_bc = R_bbx γ_b2 (h₀ — 0,5x) ≥ М

• изгибающего момента по арматуре

М_s = R_sA_sγ_s(h₀ — 0,5x) ≥ М

Эти три типа задач легко решаются с помощью таблиц.

Расчет грантовых элементов | Управление ресурсами | Финансирование Международная ассоциация развития

Формулы расчета элемента гранта (pdf)

Практическое упражнение для расчета элемента гранта
Это позволяет пользователям вводить конкретную информацию о ссуде по данному ссуде для расчета элемента ссуды.

Определение

«Льготность»

Степень льготности займа измеряется его «элементом гранта». Элемент гранта определяется как разница между номинальной стоимостью ссуды (номинальной стоимостью) и суммой дисконтированных будущих платежей по обслуживанию долга, которые должны быть произведены заемщиком (приведенная стоимость), выраженной в процентах от номинальной стоимости ссуды.Всякий раз, когда процентная ставка, взимаемая за кредит, ниже ставки дисконтирования, приведенная стоимость долга меньше его номинальной стоимости, а разница отражает (положительный) грантовый элемент кредита.

«Льготный период»

Определяется как интервал между датой обязательства и датой первого платежа основной суммы (DAC, OECD).

«Интервал»

Определяется как «интервал между датой обязательства и первой датой погашения минус интервал между двумя последовательными погашениями» (DAC, OECD).

Ставка дисконтирования

Ставки дисконтирования используются МВФ и Всемирным банком для двух основных целей в контексте долговой политики для стран с низким уровнем дохода (LIC):

• (i) оценить льготность ссуды (калькулятор «элемент гранта») при осуществлении Политики Банка по предоставлению займов на непредвиденных условиях и политики Фонда по ограничению задолженности; и
• (ii) для расчета приведенной стоимости долга в контексте структуры приемлемости долга LIC (DSF).

11 октября 2013 года исполнительные советы Фонда и Банка приняли новую упрощенную методологию, устанавливающую единую фиксированную унифицированную ставку дисконтирования для расчета грантового элемента отдельных займов. Он заменяет предыдущую систему ставок дисконтирования, основанную на специфических для валюты «коммерческих процентных ставках» (CIRR), которые были дополнительно дифференцированы в зависимости от срока погашения.

Новая ставка дисконтирования установлена ​​на уровне 5 процентов и будет рассчитываться только на основе стоимости кредита в долларах США.

,

Рассчитать баланс элементов

Здесь показано, как рассчитать баланс элементов в диаграмме рождения, чтобы определить, есть ли у вас доминирующий или слабый элемент.

Большинство карт рождения имеют довольно равномерную комбинацию элементов, что означает, что у них есть несколько планет (и асцендент), разбросанных по знакам всех четырех элементов. Однако, если у вас есть пять или более в одном элементе, вы чаще всего будете идентифицировать себя с этим доминирующим элементом, независимо от элемента вашего знака Солнца.С другой стороны, если у вас полностью отсутствует элемент или если у вас есть только одна или две планеты в одном элементе, результат будет немного другим. Отсутствие элемента (или слабого элемента, как, например, наличие 1 — 2 отсчетов) означает, что характеристики, обозначенные слабым элементом, вам нелегки. Это делает практически невозможным функционирование в режиме слабого элемента. Но, по иронии судьбы, люди с недостатком элемента обычно реагируют, компенсируя эти недостающие качества, и в итоге они ведут себя так, как будто у них этот элемент силен в их графике.Но им никогда не бывает легко. Две точки элемента указывают на незначительный недостаток; От нуля до одной точки может указывать на заметный недостаток, если в остальной части графика не существует компенсации.

Интересно отметить общий баланс элементов, но для полного портрета необходимо изучить весь график. Все всегда зависит от остальной части графика.

Обратите внимание, что существуют конкретные компенсации для слабого или недостающего элемента, которые иногда могут привести к уравновешиванию человека, если в диаграмме есть компенсации.Однако компенсации не устраняют недостаток. Вместо этого они увеличивают желание вести себя как определенный элемент, не предоставляя навыка для этого. Некоторые из этих компенсаций перечислены в интерпретациях ниже.

Наличие доминирующего или самого слабого элемента будет заметно в общем характере, но элемент каждого правителя куспида Дома покажет характер человека в сфере жизни, обозначенной каждым Домом.

Вот ключ, чтобы показать вам, какой элемент имеет каждый знак.Вы также можете использовать этот печатный лист , чтобы помочь вам.

Огонь	Земля	Air	Вода
Овен	Козерог	Весы	Рак
Лев	Телец	Водолей	Скорпион
Стрелец	Дева	Близнецы	Рыбы

Инструкция по расчетам — для оценки баланса элементов

Дайте 2 очка каждому из следующих элементов:

• элемент знака Солнца
• элемент знака Луны

Дайте 1 очко каждому из следующих элементов:

• элемент Восходящего Знака (Асцендент)
• элемент знака мизинца (М.C.)
• элемент знака Меркурия
• элемент знака Венеры
• элемент знака Марса
• элемент знака Юпитера
• элемент знака Сатурна

Добавьте дополнительное очко за каждое из следующего:

Если один из вышеперечисленных находится в 29-й степени любого знака, разделяет точку между этим элементом и элементом следующего знака, поскольку она находится так близко к 0 ° следующего знака. Так что дайте каждому элементу в этом случае пол-очка.Всего должно быть 13 баллов. Теперь подсчитайте баллы за каждый элемент.

Элемент является доминирующим, если он получает 5 или более очков, но 5 не так уж плохо. Наличие 6 или более очков является чрезмерно доминирующим.

Элемент слаб (или отсутствует), если он получает ноль баллов или 1 балл. Кроме того, если у него есть 2 или более точек, но они оказываются на более отдаленных планетах, таких как Нептун и Плутон, то считают этот элемент слабым.

Вот описания и интерпретации наличия Доминирующего Элемента или Слабого Элемента (или Недостатка Элемента):

Доминирующий огонь
Доминирующий воздух
Доминирующая земля
Доминирующая вода

Слабая (или нехватка) Огонь
Слабая (или нехватка) Воздух
Слабая (или нехватка) Земля
Слабая (или нехватка) Вода

Чтобы узнать больше о Элементах , см. Астрологический Урок 7: Элементы, Качества и Полярности .Ниже приведены интерпретации наличия Доминирующего Элемента и Слабого Элемента (Недостатка Элемента).

,

Java — Как сделать вычисления с элементами списка массивов.? Переполнение стека

1. Товары
2. Клиенты
3. Случаи использования

1. Переполнение стека Публичные вопросы и ответы
2. Команды Частные вопросы и ответы для вашей команды
3. предприятие Частные вопросы и ответы для вашего предприятия
4. работы Программирование и связанные с ним технические возможности карьерного роста
5. Талант Нанимать технический талант
6. реклама Связаться с разработчиками по всему миру

,

Конечно-элементные вычисления — Большая Химическая Энциклопедия Для описания унаследованного напряженного состояния сварного шва используются результаты моделирования методом конечных элементов. Был проведен ряд расчетов методом конечных элементов для моделирования пошаговых остаточных напряжений, а также их перераспределения в результате термообработки и эксплуатации [3]. Решения для эталонных геометрий сварного шва собраны в базе данных. При необходимости (несколько вариантов ремонта) моделирование выполняется для этого конкретного случая.[Стр.196]

Все численные расчеты неизбежно связаны с ошибками округления. Эта ошибка увеличивается с увеличением числа вычислений в процедуре решения. Следовательно, на практике последовательные уточнения сетки, которые увеличивают число вычислений конечных элементов, не обязательно приводят к более точным решениям. Однако можно предположить теоретическую ситуацию, когда ошибка округления устранена. В этом случае последовательное уменьшение размера элементов в сетке должно повысить точность решения конечных элементов.Поэтому, используя элемент «ПК» с достаточными порядками интерполяции и непрерывности, на пределе (то есть, когда размеры элемента стремятся к нулю), точное решение должно быть получено. Это было показано, что это верно для линейных эллиптических задач (Strang и Fix , 1973), где достигается оптимальная сходимость, если выполняются следующие условия … [Pg.33]

Простейшим случаем моделирования жидкости является метод, известный как вычислительная динамика жидкости. Эти вычисления моделируют жидкость как континуум, который имеет различные свойства вязкости, числа Рейнольдса и т. д.Затем поток этой жидкости моделируется с использованием численных методов, таких как вычисление методом конечных элементов, для определения свойств системы, как это предсказывается уравнением Навье-Стокса. Эти методы, как правило, являются областью инженерного сообщества и не будут обсуждаться здесь. [Pg.302]

На рисунке 21 показаны результаты конечно-элементного расчета напряжения от катода к различным точкам анода для анодной конструкции с внутренним металлическим проводником, как на рис.20. [Pg.541]

Как упомянуто в разделе 21.4.1, сообщалось о существовании промежуточной фазы с немного более жестким модулем, чем у матрицы Мббера, которая была определена методом конечных элементов. Автор сообщил, что вокруг CB имеются две фазы: одна практически сопоставима со связанной МББЭ, стекловидная фаза толщиной 2 нм (GH-фаза), другая — некроссированная непокрытая толщина 10 нм (SH-фаза). Промежуточные области в этой области обычно наблюдаются вокруг областей CB, и модуль Юнга этой области также был выше.Таким образом, существует вероятность того, что SH-фаза впервые наблюдалась непосредственно в реальном пространстве. [Pg.602]

Рис. 50. (a) Первичное распределение потенциала, окружающее электрод в форме диска. (Перепечатано с разрешения ссылки 47. Copyright 2004 John Wiley Sons.) (B) Конечно-элементный расчет 2D первичного потенциального профиля вблизи электрода с регулярным периодическим контактом с электролитом.

Контурная диаграмма

— это линии постоянного потенциала, за которыми следуют вертикальные линии текущий путь.[Pg.594]

Рисунок 54. Измеренный (а) и смоделированный (б) эффект смещения электродов, (а) Полное сопротивление ячеек и шаровых ячеек симметричной ячейки LSC / редкоземельного элемента церия / LSC с номинально идентичной пористой LSC x = 0,4) электроды, измеренные при температуре 750 ° С на воздухе в зависимости от геометрии ячейки. (b) Расчет методом конечных элементов полного сопротивления ячеек и половин ячеек симметричной ячейки с идентичными электродами R-C, предполагая смещение двух рабочих электродов (d), равное толщине электролита (L)….

000203068013242.png» alt=»Figure 54. Measured (a) and simulated (b) effect of electrode misalignment, (a) Total-cell and balf-cell impedances of a symmetric LSC/rare-earth-doped ceria/LSC cell with nominally identical porous LSC x= 0.4) electrodes, measured at 750 °C in air based on tbe cell geometry shown. (b) Finite-element calculation of tbe total-cell and half-cell impedances of a symmetric cell with identical R—C electrodes, assuming a misalignment of the two working electrodes (d) equal to the thickness of the electrolyte (L). …» />

Рис. 9.12. Точность аналитического выражения. Сравнение уравнения (9.30) с конечно-элементным вычислением Карра (1988). (Воспроизведено с Чена, 1992, с разрешения.) …

Рис.8.9. Напряженные поля в конце траншеи, вытравленной в 15f

Самый высокий уровень группировки в иерархии называется доменом. Этот термин обычно используется в вычислениях конечных элементов для обозначения различных областей задачи, где могут быть разные физические свойства или определяющие уравнения. В этом смысле мы используем этот термин. Поскольку в двух пространственных областях, например, в газе и на реактивной поверхности, может происходить принципиально различный химический состав реакции, удобно разделить расчет на области.[Pg.447]

Рис. 5a-c Значения главных напряжений для прямоугольных стержней, нагруженных по их длине при растяжении силами, приложенными к четырем углам. (Расчеты методом конечных элементов в плоской деформации), соотношение сторон изотропного материала 5 b Соотношение сторон изотропного материала 10 c Анизотропный материал (E / G), n = 15,1, соотношение сторон 10 (обратите внимание, что рисунки выполнены не в масштабе). (Из ссылки 16) … [стр.91]

Рис. 6. Деформация растяжения вдоль направления нагрузки на поверхности (вверху) и в центре (внизу) в прямоугольном стержне, нагруженном по его длине силами на его четырех углах.(Конечно-элементные расчеты в плоской деформации). Анизотропный материал (E / G) 1 2 = 15,1. Соотношение сторон 40/3 …

M.F. Horstemeyer и др. Микромеханические расчеты методом конечных элементов температуры и влияния конфигурации пустот на рост и коалесценцию пустот. Int J. Plasticity 16, 979-1015 (2000) … [Pg.127]

Рис. 14. Гипотетическое двухзеренное с микроэлектродами (а) и квадратными электродами по бокам (б).(d) Распределение плотности тока в плоскости границы зерен образца из 24 зерен и эскиз границ зерен, для которых построено распределение плотности тока (c). Параметры, используемые в расчетах методом конечных элементов dms = 1/5 Lg, wgb = 10 3 Lg и p b = 105 phvSk для всех границ зерен. Пики из-за числовых ошибок. Вследствие вычислительных причин рассматриваемая плоскость является не самой плоскостью границы зерен, а плоскостью на расстоянии 0,052 от границ зерен.

Поэтому давайте вместо этого рассмотрим более практичный случай распределения третичного тока. Исходя из зависимости числа Вагнера от наклона поляризации, мы можем предсказать, что труба, катодно защищенная от плотности тока вблизи плотности катодного тока, ограниченного массопереносом, будет иметь более равномерное распределение тока, чем труба, работающая под управлением переноса заряда.Конечно, плотность катодного тока не может превышать ограниченное значение массопереноса в любом месте на трубе, как сказано в главе 4. Рассмотрим трубу с катодной защитой на входе с цинковым анодом в нейтральной морской воде (4). Поскольку реакция восстановления кислорода ограничена массопереносом, число Вагнера велико для трубы с катодной защитой (рис. 12а), и прогнозируется относительно равномерное распределение тока. Однако, если проводимость раствора снижается, распределение тока станет менее равномерным.Конечно-элементные расчеты и экспериментальные подтверждения (рис. 12б) подтверждают качественные результаты числа Вагнера (4). [Pg.200]

Не было предпринято никаких попыток всесторонне обсудить модели, основанные на конечно-элементных расчетах или других численных анализах. Обсуждались только некоторые результаты Schmauder и McMeeking10 для поперечной ползучести степенных материалов. Основная причина того, что такие анализы, как правило, были опущены, заключается в том, что они, как правило, встречаются в литературе по небольшому числу конкретных проблем, и мало что сделано для обеспечения всеобъемлющих результатов для диапазона параметров, которые были бы технически интересны, ,то есть, объемные доли арматуры от нуля до 60%, пропорции армирования от 1 до 106 и т. д. Внимание в этой главе ограничивалось случаями, когда можно было бы представить всеобъемлющие результаты. Почти во всех случаях это означает, что для использования были доступны только приблизительные модели. [Pg.329]

Ошибки являются результатом упругой и пластической природы самих керамических частиц. Несколько других авторов [81,82] вычислили распределение давления в цилиндрических матрицах и других формах, используя конечно-элементные численные методы.Борцмейер [81] включил когезию, упругую и пластическую деформацию частиц в расчеты методом конечных элементов для более сложных геометрий, как показано в … [Pg.665]

Влияние различных типов прослойки на термоупругие остаточные напряжения может быть проанализирован из расчетов методом конечных элементов для двумерной геометрии, при условии идеального соблюдения и без учета какой-либо реактивности между компонентами. [Pg.70]

Первая часть статьи посвящена разработке образца с надрезом и анализу полученного коэффициента интенсивности напряжений для расчета методом конечных элементов.Вторая часть посвящена практической подготовке образцов. В третьей части рассказывается об эволюции ударной вязкости и анализе полей вершины трещины со скоростью нагружения для ПММА и ПК. Влияние радиуса надреза также учитывается. [Стр.29]

Во-первых, распределения упругих напряжений образцов без надреза получают из анализа методом конечных элементов. Для образца без надреза PI несоответствие между конечным элементом и аналитическим результатом очень мало (около 0.01%), что подтверждает правильность расчета методом конечных элементов с точки зрения точности через сетку и тип используемого элемента. Поэтому аналогичный расчет проводится для образца без надреза G1, где отношение пролета к высоте меньше. Несовпадение максимальных напряжений в нижней и верхней частях балки между расчетами методом конечных элементов и аналитическим решением составляет 0,74% при растяжении и 0,79% при сжатии (и остается постоянным при дальнейшем уточнении сетки). Эта оценка распределения напряжения затем используется для следующей оценки коэффициента интенсивности напряжения.[Стр.30]

Рис.2. Сравнение SIF одиночного надреза при чистом изгибе (Ki) и из расчета методом конечных элементов конфигурации без зазоров G1 (Ki). Различные значения x представляют увеличение от центра, нормализованное по внутреннему диапазону.

Было установлено, что формула (6) приводит к лучшим результатам даже для очень коротких трещин.В этом сравнительно-теоретическом анализе прогиб d в формулах (5) — (7) взят из расчетов методом конечных элементов. [Pg.519]

В настоящей статье метод граничных конечных элементов представлен как метод граничной дискретизации для численного исследования концентраций межфазных напряжений в композитных ламинатах. В отличие от классического метода граничных элементов, формулировка элементов основана на конечных элементах, что позволяет избежать необходимости фундаментального решения. Сравнительные результаты расчетов методом конечных элементов показывают хорошее согласие как для эффекта свободного края ламината, так и для примера концентраций напряжений вблизи трещин в композитных ламинатах.[Pg.539]

Рис. 3.8. Две различные собственные функции для квантового загона, полученные с помощью двумерного вычисления конечных элементов (любезно предоставлено Harley Johnson).

Численный расчет двумерных форм равновесия. Чтобы выйти за рамки относительной простоты набора форм, рассматриваемых в представленном выше анализе, необходимо прибегнуть к численным процедурам.В качестве предварительного к численным результатам, которые будут рассмотрены ниже и которые требуются при столкновении со всей сложностью как произвольных вариаций формы, так и полной упругой анизотропии, мы отмечаем серию расчетов с конечными элементами, которые были сделаны (Jog et al. 2000 ) для более широкого класса геометрий, чем те, которые рассматривались Джонсоном и Каном. Представленный выше анализ был основан на способности извлекать аналитические описания как поверхностных, так и упругих энергий для ограниченного класса геометрий.Более общие геометрии противостоят аналитическому описанию, и, следовательно, упругая часть проблемы (как минимум) должна быть решена путем использования численных методов. [Pg.534]

В качестве дополнительного подхода метод среднего поля используется в сочетании с методом конечных элементов для исследования УЖГ. Чтобы сравнить прогнозы с периодическим моделированием элементарной ячейки, часть FGM делится на девять подуровней. Каждый из них состоит из двух биквадратичных 8-узловых плоских элементов по толщине, и только один элемент используется в горизонтальном направлении.Части чистого глинозема и чистого никеля моделируются тремя и 12 элементами соответственно. В каждом подслое объемные доли фаз постоянны. Кроме того, центральный подслой можно разделить на полуподслой с металлической матрицей и керамической матрицей. Свойства конкретного материала на мезоструктурном уровне в рамках расчета методом конечных элементов описываются с помощью констант … [Pg.76]

Результаты периодической элементарной ячейки прямо сопоставимы с предсказаниями IMT, поскольку оба подхода представляют та же матрица / микроструктура типа включения.Однако такие сравнения должны проводиться осторожно, поскольку некоторые предположения, касающиеся расчетов с использованием конечных элементов, не эквивалентны для подходов с расширенной элементарной ячейкой и настоящего метода среднего поля. Анализ напряжений в плоскости моделей элементарной ячейки не учитывает ограничения в неплоском направлении. Напротив, в рамках настоящей композиции IMT включения трехмерно заключены в матричный материал. В отличие от моделей элементарных ячеек плоского напряжения учитывается ограничение в неплоскостном направлении.Соответственно, эти прогнозы обозначаются как полное внутреннее ограничение. Чтобы преодолеть это внутреннее ограничение, чтобы смоделировать модель плоского напряжения, предположим -… [Pg.78]

---

,

Previous Post

Биозащита древесины своими руками – Пропитка для дерева от влаги и гниения, выбираем антисептики для дерева для наружных работ | Журнал Дока | Деревянные материалы и их применение в строительстве

Next Post

Приспособление для заточки ножей своими руками: Приспособления для заточки ножей своими руками: чертежи, видео – Приспособление для заточки ножей своими руками – чертежи, пошаговая инструкция

Related Articles

19 июня, 2020 alexxlab

Ендова верхняя ендова нижняя фото – что это такое (фото), монтаж соединения двух ендов на скате (верхняя и нижняя), устройство обрешетки и стропил

Содержание Ендова верхняя и нижняя фото — Портал о стройкеЧто такое ендоваТипы ендовКакой материал выбратьВидео: внутреннее устройство ендовыМонтаж ендовы своими рукамиВидео: монтаж нижней ендовы с выходом на скатСоветы специалистов7. Устройство ендов ☛ СТэПЕндова верхняя ендова нижняя фото — Сайт о дачеЧто такое ендова и ее видыХарактеристики ендовы ОндулинГде и как устанавливается ендова Ондулин?Плюсы использования ендовы ОндулинКак рассчитать нужное […]

Читать далее

2 февраля, 1970 alexxlab

С 8 профлист размеры: Профнастил С8-1150 со склада с доставкой — купить по цене производителя

Содержание Характеристики профлиста С-8. Что нужно о нём знать?Как выглядит профнастил С-8?Что означает маркировка профлиста С-8?Каковы технические характеристики профнастила С-8?Из стали какой толщины изготавливают профлист С-8?Какой вид профнастила С-8 лучше: с полимерным покрытием или без него? В каких покрытиях изготавливается профлист С-8?Каковы преимущества профнастила С-8?В статье упоминаются категории:В статье упоминаются товары:размеры листа, технические характеристики, весТехнология […]

Читать далее

21 декабря, 1970 alexxlab

Укладка гибкой черепицы своими руками: Технология монтажа гибкой черепицы (мягкой кровли) своими руками: пошаговая инструкция

Содержание Монтаж мягкой черепицы своими руками, инструкция, фото, видеоКровельный пирог для мягкой черепицыГидроизоляцияОбрешеткаНастилТехнология настила кровли из мягкой черепицыУсиление свесаУкладка гидроизоляционного ковраПодкладочный коверФронтонная (торцевая) планкаРазметка скатаЕндовный коверПримыкание к кирпичной трубеВывод круглых трубСтартовая полосаМонтаж мягкой рядовой черепицыОформление ендовыОформление фронтона Установка конькаРебра и перегибыКак укладывать гибкую черепицу крышу. Мягкая кровля своими руками – монтаж мягкой черепицы. Подготовительный этап к монтажу […]

Читать далее

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт