Расчет балки на изгиб сопромат – Расчет балок на прочность он-лайн. Расчет балки на изгиб. Расчет балки. Шаг 1. Количество узлов.

Задачи на изгиб | ПроСопромат.ру

Проектный и проверочный расчеты. Для балки с построенными эпюрами внутренних усилий  подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность  балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано:

Покажем балку с построенными эпюрами Q и М

Согласно эпюре изгибающих моментов опасным является сечение С, в котором М_С=М_max=48,3кНм.

Условие прочности по нормальным напряжениям для данной балки имеет вид σ_max=M_C/W_X

Определим необходимое расчетное значение осевого момента сопротивления сечения:

Для сечения в виде двух швеллеров согласно сортаменту прокатной стали принимаем два швеллера №20а, момент инерции каждого швеллера I_x=1670см⁴, тогда осевой момент сопротивления всего сечения:

Перенапряжение (недонапряжение) в опасных точках  посчитаем по формуле: Тогда получим недонапряжение:

Теперь проверим прочность балки, исходя из условия прочности по касательным напряжениям. 

Условие прочности по касательным напряжениям имеет вид:

Для швеллера №20 а:  статический момент площади S_x1=95,9 см³, момент инерции сечения I_x1=1670 см⁴, толщина стенки d₁=5,2 мм, средняя толщина полки t

Для поперечного сечения из двух швеллеров:

S_x= 2S_x1=2·95,9=191,8 см³,

I_x=2I_x1=2·1670=3340 см⁴,

b=2d₁=2·0,52=1,04 см.

Определяем значение максимального касательного  напряжения:

τ_max=48,9·10³·191,8·10⁻⁶/3340·10⁻⁸·1,04·10⁻²=27МПа.

Как видно, τ_max <τ_adm

Следовательно, условие прочности выполняется.

Проверяем прочность балки по энергетическому критерию.

Из рассмотрения эпюр Q и М следует, что опасным является сечение С, в котором действуют M_C=M_max=48,3 кНм и Q_C=Q_max=48,9 кН.

Проведем анализ напряженного состояния в точках сечения С 

Схема сечения балки и эпюры напряжений для анализа напряженного состояния

Определим нормальные и касательные напряжения на нескольких уровнях (отмечены на схеме сечения)

Уровень 1-1: y_1-1=h₁/2=20/2=10см.

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 2−2: y_2-2=h₁/2−t₁=20/2−0,97=9,03см.

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 3−3: y_3-3=h₁/2−t₁=20/2−0,97=9,03см.

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 4−4:    y_4-4=0.

Нормальные и касательные напряжения:(в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 5−5:

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 6−6:

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

 Уровень 7−7:

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

В соответствии с выполненными расчетами эпюры напряжений σ, τ, σ₁, σ₃, τ_max и τ_min представлены на рис. Схема сечения балки и эпюры напряжений для анализа напряженного состояния

Анализ этих эпюр показывает, что в сечении балки опасными являются точки на уровне 3-3 (или 5-5), в которых: 

Используя энергетический критерий прочности, получим

Из сравнения эквивалентного и допускаемого напряжений следует, что условие прочности также выполняется  

 (135,3 МПа<150 МПа).

prosopromat.ru

Расчет на прочность | ПроСопромат.ру

Задача 1

В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.

Требуется:

а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,

б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.

Решение

а) Для определения σ_(К), τ_(К) и _maxσ,_maxτ потребуется знать величины осевого момента инерции всего сечения I_Н.О., осевого момента сопротивления W_Н.О., статического момента отсечённой части  и статического момента половины сечения S_max:

Тогда:

б) Проверка прочности:

— по условию прочности нормальных напряжений:

— по условию прочности касательных напряжений:

Задача 2

В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.

где 

Тогда

где:

Тогда

Задача 3

Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.

Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:

(1)          ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,

откуда 

(2)          ∑М(А) = F·2 – М + В·6 — (q·6)·3 =0,

откуда 

Iучасток   

∑М(С) = М(z₁) +F·z₁=0,

ММ(z₁) = —F·z₁= — 30 ·z₁ —

– уравнение прямой.

При z₁ = 0:      М = 0,

z₁ = 2:      М =- 60 кНм.

∑у= — F — Q(z₁) = 0,

Q(z₁) = — F = -30 кН – постоянная функция.

II участок     

откуда

— уравнение параболы.

При z₂=0:     М = 0,

z₂=3м:  М = 30 · 3 – 5 · 3² = 90 — 45 = 45кНм,

z₂=6м:  М = 30 · 6 – 5 · 6² = 180 — 180 = 0.

∑у= Q(z₂) — q·z₂ + B= 0,

Q(z₂) = q·z₂ — B= 10·z₂ – 30 – уравнение прямой,

при  z₂ = 0:     Q = -30,

        z₂ = 6м:     Q = 10·6 – 30 = 30.

Определение аналитического максимума изгибающего момента второго участка:

из условиянаходим :

И тогда

Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.

Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.

В данном случае максимальный момент по модулю М = 60кНм

откуда: :

а) сечение круглой формы d=?

б) сечение прямоугольной формы при h/b = 2:

тогда

Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:

Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:

— для круглого сечения 

— для прямоугольного сечения 

Воспользуемся этими формулами. Тогда

— для балки круглого сечения при :

— для балки прямоугольного сечения

Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:

А_{прямоугольного} = 865,3см² < А_{круглого} = 1218,6см², следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.

Задача 4

Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа. 

Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:

(1)              ∑М(А) = – М₁– F  ·2 — (q·8)·4 + М₂ + В·6 =0,

откуда 

(2)      ∑М(В) = – М₁– А · 6 + F · 4 + (q·8)·2 + М₂ =0,

откуда 

Проверка:

∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.

∑М(С) = М(z₁) — М₁=0,

М(z₁) = М₁= 40 кНм – постоянная функция.   

∑у= — Q(z₁) = 0,

Q(z₁) = 0.

II участок 

— парабола.

Приz₂=0:       М = 40 кНм,

z₂=1м:    М = 40 + 104 – 10=134кНм,

z₂=2м:    М = 40+ 104 · 2 – 10 · 2² = 208 кНм.

∑у=А — q·z₂ — Q(z₂) = 0,

Q(z₂) =А— q·z₂ = 104 –  20·z₂  – уравнение прямой,

при  z₂ = 0:       Q = 104кН,

        z₂ = 6м:    Q = 104 – 40 = 64кН.

III участок

— парабола.

Приz₃=0:       М = 24+40=-16 кНм,

z₃=2м:    М = 24 + 136·2 — 10 (2+2)² = 24 + 272 – 160 = 136кНм,

z₃=4м:    М = 24 + 136·4 – 10 (2+4)² = 24 + 544 – 360 = 208 кНм.

∑у=В — q(2+z₃ ) + Q(z₃) = 0,

Q(z₃) =- В + q(2+z₃ ) = -136 + 20 (2+z₃ )   – уравнение прямой,

при  z₃ = 0:        Q = -136 + 40 = — 94кН,

        z₃ = 4м:     Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.

IV участок

— парабола.

z₄=0:       М = 0кНм,

z₄=1м:    М = – 10кНм,

z₄=2м:    М = — 40кНм.

∑у=- q·z₄ + Q(z₄) = 0,

Q(z₄) =q·z₄ = 20·z₄  – уравнение прямой.

Приz₄ = 0:       Q = 0,

        z₄ = 2м:     Q = 40кН.

Проверяем скачки в эпюрах:

а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М₂=24, приложенному в этом месте.

б) В эпюре Q три скачка:

первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,

второй – под силой F=80кН и равен ей (64+16=80кН),

третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)

Наконец, проектируем двутавровое сечение.

Подбор его размеров производится из условия прочности по нормальным напряжениям :

В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления W_х нет. Есть № 40^а с W_х=1190 см³ и № 45^а с W_х=1430 см³

Попробуем  меньший из них. Если принять двутавр № 40^а, у которого W_х=1190 см³ , то наибольшее напряжение в опасном сечении будет:

и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.

Поэтому приходится принимать ближайший больший размер двутавра, а именно №45^а, у которого W_х=1430 см³. В этом случае балка будет работать с недонапряжением:

что меньше [σ]=160МПа на  

Итак, принимается двутавр №45^а, у которого: W_х=1430 см³, I_х=32240см⁴, I_х: S_х=38,6см, d=11,5мм.

Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :

Это условие прочности выполняется, даже с избыточным запасом.

Задача 5

Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).

Решение 

1.Определение опорных реакций 

∑М(А) = F · 2 + М₁ — М₂— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М₁— М₂ – А · 8 + q·6·1 =0,Проверка:

∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.

2.Построение эпюр изгибающих моментов и поперечных сил.

I участок

∑М(С) = М(z₁) + F·z₁=0,

М(z₁) = — F·z₁= -20·z₁.

При z₁=0:     М = 0,

        z₁=2м:  М = – 40кНм,

∑у= — F— Q(z₁) = 0,

Q(z₁) = — 20кН.

II участок

        z₂=0:      М = — 20 – 40 = -60 кНм,

z₂=4м:   М = 200 — 20 – 120 = 200 — 140 = 60кНм.

∑у=- F + А — Q(z₂) = 0,

Q =- F + А= -20+50=30кН.

III участок

— парабола.

Приz₃=0:      М = — 20·4= — 80 кНм,

z₃=2м:   М = 210·2 — 20·(2+2)² = 420 – 320 = 100кНм,

z₃=4м:   М = 210·4 – 20 · (2+4)² = 840 – 720 = 120кНм.

∑у= Q(z₃) + В — q·(2+z₃) = 0,

Q(z₃) = — В + q·(2+z₃) = — 210 + 40·(2+z₃) – уравнение прямой.

Приz₃ = 0:       Q = -130кН,

        z₃ = 4м:     Q = 30кН.

Q(z₀) = — 210 + 40·(2+z₀) = 0,

— 210 + 80 + 40·z₀ = 0,

40·z₀ = 130,

z₀ =3,25м,

IV участок

парабола.

Приz₄=0:      М = 0 кНм,

z₄=1м:   М = – 20кНм,

z₄=2м:   М = — 80кНм.

∑у=- q·z₄ + Q(z₄) = 0,

Q(z₄) =q·z₄ = 40·z₄  – уравнение прямой,

        z₄ = 0:        Q = 0,

        z₄ = 2м:     Q = 80кН.

3. Подбор сечений (опасное сечение по σ: |_maxМ|=131,25кНм,

опасное сечение по τ: |_maxQ|=130кН).

Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)

Принимаем: В=0,24м,

                         Н=0,48м.

Проверяем по τ:

Вариант 2. Деревянное круглое

Принимаем d=0,45м,

Проверяем по τ:

Вариант 3. Чугун : ([σ_Р]=30МПа, [σ_с]=120МПа, [τ]=15МПа)

Принимаем b=0,19м, тогда h=0,38м, d=0,076м.

Проверка по τ:

b(у)= b — d= 0,19 — 0,076 = 0,114м

Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).

по сортаменту W_х=953см³. Это №40: I_x=19062см⁴, S_х=545см³, d=0,83см.

Проверка по τ:

Вариант 5. Сталь, круглая труба

Принимаем D=0,22м   →  d = 0,6·D =0,132м.

Проверка по τ:

Вариант 6. Сталь, прямоугольная труба  

b₁= b — 2t = b — 2·0,1b = 0,8b,

h₁= h — 2t  = 0,8h,

Принимаем b=0,13м, h=0,26м.

Проверка по τ:

Кстати: какое из сечений стальной балки выгодней по расходу материала?

Двутавр —  А = 72,6см² = 72,6·10^-4 = 0,00726м²,

круглая труба –

прямоугольная труба — 

Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.

prosopromat.ru

Изгиб | ПроСопромат.ру

При выводе формулы для вычисления нормальных напряжений рассмотрим такой случай изгиба, когда внутренние силы в сечениях балки приводятся только к изгибающему моменту, а поперечная сила оказывается равной нулю. Этот случай изгиба носит название чистого изгиба. Рассмотрим средний участок балки, подвергающийся чистому изгибу.

В нагруженном состоянии балка прогибается так,что ее нижние волокна удлиняются,а верхние укорачиваются.

Поскольку часть волокон балки растягивается, а часть сжимается, причем переход от растяжения к сжатию происходит плавно, без скачков, в средней части балки находится слой, волокна которого только искривляются, но не испытывают ни растяжения, ни сжатия. Такой слой называют нейтральным слоем. Линия, по которой нейтральный слой пересекается с поперечным сечением балки, называется нейтральной линией или нейтральной осью сечения. Нейтральные линии нанизаны на ось балки. Нейтральная линия — это линия, в которой нормальные напряжения равны нулю.

Линии, проведенные на боковой поверхности балки перпендикулярно оси, остаются плоскими при изгибе. Эти опытные данные позволяют положить в основу выводов формул гипотезу плоских сечений (гипотеза Бернулли). Согласно этой гипотезе сечения балки плоские и перпендикулярные к ее оси до изгиба, остаются плоскими и оказываются перпендикулярными изогнутой оси балки при ее изгибе.

Допущения для вывода формул нормального напряжения: 1)   Выполняется гипотеза плоских сечений.   2)   Продольные волокна друг на друга не давят (гипотеза о ненадавливании) и, следовательно, каждое из волокон находится в состоянии одноосного растяжения или сжатия.  3)   Деформации волокон не зависят от их положения по ширине сечения. Следовательно, и нормальные напряжения, изменяясь по высоте сечения, остаются по ширине одинаковыми.   4)   Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости.   5)   Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков.   6)   Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.

Рассмотрим балку произвольного сечения, но имеющую ось симметрии.Изгибающий момент представляет собой результирующий момент внутренних нормальных сил, возникающих на бесконечно малых площадках и может быть выражен в интегральном виде:  (1), где y — плечо элементарной силы относительно оси х

Формула (1) выражает статическую сторону задачи об изгибе прямого бруса, но по ней по известному изгибающему моменту нельзя определить нормальные напряжения, пока не установлен закон их распределения. 

Выделим на среднем участке балки и рассмотрим участок  длиной dz, подвергающийся изгибу. Изобразим его в укрупненном масштабе.

К выводу формул при изгибе: а) участок балки до деформации; б) участок балки после деформации

Сечения, ограничивающие участок dz, параллельны друг другу до деформации, а после приложения нагрузки повернутся вокруг своих нейтральных линий на угол . Длина отрезка волокон нейтрального слоя при этом не изменится и будет равна:, где  -это радиус кривизны изогнутой оси балки. А вот любое другое волокно, лежащее ниже или выше нейтрального слоя, изменит свою длину. Вычислим относительное удлинение волокон, находящихся от нейтрального слоя на расстоянии у. Относительное удлинение — это отношение абсолютной деформации к первоначальной длине ,тогда:

 Сократим на и приведем подобные члены, тогда получим:(2) Эта  формула выражает геометрическую сторону задачи о чистом изгибе: деформации волокон прямо пропорциональны их расстояниям до нейтрального слоя. 

Теперь перейдем к напряжениям, т.е. будем рассматривать физическую сторону задачи. в соответствии с допущением о ненадавливании волокон используем закон Гука при осевом растяжении-сжатии:, тогда с учетом формулы (2) имеем (3),т.е.  нормальные напряжения при изгибе по высоте сечения распределяются по линейному закону. На крайних волокнах нормальные напряжения достигают максимального значения, а в центре тяжести сечения равны нулю. Подставим  (3) в уравнение (1) и вынесем за знак интеграла дробь  как постоянную величину, тогда имеем. Но выражение  — это осевой момент инерции сечения относительно оси х  — I_х. Его размерность см⁴, м⁴

Тогда ,откуда (4) ,где — это кривизна изогнутой оси балки, а — жесткость сечения балки при изгибе.

Подставим полученное выражение кривизны (4) в выражение (3) и получим формулу для вычисления нормальных напряжений в любой точке поперечного сечения: (5) 

Т.о. максимальные напряжения возникают в точках, наиболее удаленных от нейтральной линии. Отношение  (6) называют осевым моментом сопротивления сечения. Его размерность см³, м³. Момент сопротивления характеризует влияние формы и размеров поперечного сечения на величину напряжений.

Тогда максимальные напряжения:  (7)

Условие прочности при изгибе: (8)

При поперечном изгибе действуют не только нормальные, но и касательные напряжения,т.к. имеется поперечная сила. Касательные напряжения усложняют картину деформирования, они приводят к искривлению поперечных сечений балки, в результате чего нарушается гипотеза плоских сечений. Однако исследования показывают, что искажения, которые привносят касательные напряжения, незначительно влияют на нормальные напряжения,подсчитанные по формуле (5). Таким образом ,при определении нормальных напряжений в случае поперечного изгиба теория чистого изгиба вполне применима.

Нейтральная линия. Вопрос о положении нейтральной линии. 

При изгибе отсутствует продольная сила, поэтому можно записать Подставим сюда формулу нормальных напряжений (3) и получим Так как модуль продольной упругости материала балки не равняется нулю и изогнутая ось балки имеет конечный радиус кривизны, остается положить, что  этот интеграл представляет собой статический момент площади поперечного сечения балки относительно нейтральной линии-оси х , и, поскольку он равен нулю, то нейтральная линия проходит через центр тяжести сечения.

Условие  (отсутствие момента внутренних сил относительно силовой линии) даст или с учетом (3) . По тем же соображениям (см. выше) . В подынтегральном выражении — центробежный момент инерции сечения относительно осей х и у  равен нулю, значит, эти оси являются главными и центральными и составляют прямой угол. Следовательно, силовая и нейтральная линии пр  прямом изгибе взаимно перпендикулярны. 

Установив положение нейтральной линии, несложно построить эпюру нормальных напряжений по высоте сечения. Ее линейный характер определяется уравнением первой степени.

Характер эпюры σ для симметричных сечений относительно нейтральной линии, М<0

prosopromat.ru

Построение эпюр при изгибе для балки

Привет! Вы находитесь на сайте – sopromats.ru, проекте о сопромате и не только! Это новая статья из серии – «сопромат для чайников», в которой я расскажу о построении эпюр при изгибе для балки. Как обычно, буду писать просто и по делу. Здесь я не буду спамить специфическими фразами из сопромата и рассматривать сложные примеры. Будем учиться на простейшей балке. Ну что же давайте начнем учиться!

Сколько можно нарисовать эпюр при изгибе для балок?

Для простого изгиба, который будем рассматривать в этой статье, можно нарисовать всего две эпюры. Одна именуется как эпюра поперечных сил, другая зовется эпюрой изгибающих моментов. Одна показывает распределение внутренних сил внутри элемента, работающего на изгиб, другая моментов. Если хотите, можете изучить больше информации по этим силовым факторам в следующих материалах:

• Как построить эпюру поперечных сил? Здесь вы можете найти полное досье на поперечную силу: кто такая, зачем нужна и как обозначается. Тут же можно почитать подробную инструкцию по построению эпюры этой величины. В статье рассказано про 3 методики расчета и построения.
• Как построить эпюру изгибающих моментов? В этом материале можно узнать много всего об изгибающем моменте. Например, зачем он нужен и как определяется, как обозначается и в чем измеряется. А также подробнейшим образом изучить методики построения эпюры этой величины, 3-мя способами.

Если Вам лень читать эти статьи, то ничего. Это нормально 🙂 Просто хотел пропиарить немного эти материалы, не зря же я их писал…В этой статье, для чайников, мы, итак, научимся строить эти эпюры, но только одним методом.

Подготовительные работы

Для того, чтобы построить эпюры, первым делом вычертите расчетную схему, с указанием всех нагрузок и размеров:

После этого нужно определить реакции опор. Без них дальше никуда. Если Вы не умеет этого делать, обязательно прочтите этот урок про расчет реакций опор для чайников. Здесь же сразу приведу результат вычислений:

Расчет и построение эпюр

Для расчета эпюр сначала нужно наметить участки, на которых эпюра будет либо постоянна, либо меняться по одному закону. Опознать эти участки достаточно просто. Границами участков служат те места, где прикладываются нагрузки (сосредоточенные силы и моменты, в том числе реакции опор). Если на балку действует распределенная нагрузка, то границы – это ее начало и конец. В нашем случае, как видите, 2 участка, каждый по 2 метра:

Рассматриваем произвольное сечение первого участка, которое обзовем буквой – С. Оно будет находится на расстоянии z1 от левого торца балки. И относительного него будем записывать законы, по которым меняются поперечные силы и изгибающие моменты на этом участке:

Записываем уравнение для поперечной силы

Поперечная сила будет равняться сумме всех сосредоточенных сил, находящихся слева от сечения (или справа). Мы будем подсчитывать все, что находится слева, т.к. там меньше нагрузки. В уравнении поперечной силы, все внешние нагрузки нужно учитывать с учетом правила знаков: если сила, относительно рассматриваемого сечения, поворачивает ПО часовой стрелке, то в уравнение она пойдет с ПЛЮСОМ (и наоборот).

В рассматриваемом примере, реакция RA поворачивает ПО часовой стрелке, и уравнение получится такое:

Причем, как видно, эта зависимость справедлива для любого сечения на первом участке, тем самым поперечная сила в пределах этого участка постоянна и равна – 5 кН. Откладываем это значение на графике:

Эпюры заштриховываются перпендикулярно нулевой линии и на каждом участке проставляются знаки поперечной силы.

Записываем уравнение для изгибающего момента

Что касается изгибающего момента, то тут в уравнении нужно учесть сумму моментов, находящихся по одну сторону от сечения. Реакция RA, относительно сечения С создает момент RA·z1. Напомню, что момент – это сила, умноженная на плечо. Где плечо – это расстояние от силы до центра момента (в этом случае, центр – это рассматриваемое сечение). В уравнении моментов, все моменты нужно учитывать с учетом правила знаков: если момент силы, стремится растянуть нижние волокна, то в уравнении будем записывать его со знаком «+». И наоборот.

Придерживаясь этого правила, будем откладывать эпюры изгибающих моментов со стороны РАСТЯНУТЫХ волокон. Что практикуется у инженеров-строителей. У механиков, другие правила, они рисуют эти эпюры со стороны сжатых волокон. Кстати, что такое растянутое и сжатое волокно? Покажу на нашем же примере:

Как видно, сила RA, при повороте, стремится растянуть нижние волокна, поэтому в уравнение будем записывать момент этой силы со знаком плюс:

Анализируя это уравнение, видим, что изгибающий момент будет меняться по линейному закону и зависеть от координаты z1. И чтобы рассчитать и построить эпюру на этом участке достаточно подставить в уравнение координаты начала участка z1=0 и конца z1=2 м. После чего отложить эти точки на графике и соединить прямой линией:

Эпюры для второго участка балки

С учетом всех вышеописанных рекомендаций, я думаю Вы сами теперь сможете построить эпюры для второго участка. Подробно комментировать уже не буду, приведу сразу решение и окончательные эпюры для этой балки:

Сегодня мы рассмотрели урок по построению эпюр для простой балки. Однако, много нюансов по расчету и построению я не рассказал, т.к. все это уместить в одном уроке, довольно сложно и не всем это нужно, статья ведь для чайников! Если Вы хотите прокачать свой знания, в этих вопросах, обязательно прочитайте эти материалы о эпюрах. Здесь можно найти подробные статьи о поперечной силе, о изгибающем моменте. Где я рассказывал о 3-х методиках расчета, причем один из них, даже проще, чем мы рассматривали в данной статье. С помощью которого можно устно рисовать эти эпюры. Также там можно посмотреть, как учитывать моменты и распределенные нагрузки при расчете эпюр и какие особенности есть по построению при действии данных видов нагрузок.

Спасибо за внимание! Если Вам понравилась статья, да и сайт в целом, добавляйте его в свои закладки, чтобы иметь быстрый доступ к нему, а также подписывайтесь на наши соц. сети, делитесь этой статьей с друзьями и т.д. Буду благодарен 🙂

sopromats.ru

Расчёт балки бесплатно онлайн

Закрыть

Примечание. Иллюстрации в отчёте сформированы шириной в 420px (диалог «Настройки»).

Исходные данные

L = 10м; q = 12кН/м; M = 15кН·м; F = 19кН.

Рис. 1. Исходная схема

Расчёт

Рис. 2. Схема реакций

Рис. 3. Эпюра Qy, кН (поперечная сила)

Рис. 4. Эпюра Mx, кН·м (изгибающий момент)

1. Определение реакций опор

Составим уравнения статического равновесия.

∑F_y = -q·7м — F + Y_A + Y_B = 0;

∑M_A = -q·7м·3.5м + M — F·10м + Y_B·7м = 0.

Решение уравнений статики даёт следующие значения реакций:

Y_A = 36кН;

Y_B = 67кН.

2. Построение эпюр внутренних силовых факторов

Участок №1 (0 ≤ z₁ ≤ 7м)

Q_y = Y_A — q·z₁;

при z₁ = 0; Q_y = 36кН.

при z₁ = 7м; Q_y = -48кН.

M_x = Y_A·z₁ — q·z₁²/2;

при z₁ = 0; M_x = 0.

при z₁ = 3м; M_x = 54кН·м.

при z₁ = 7м; M_x = -42кН·м.

Участок №2 (0 ≤ z₂ ≤ 3м)

Q_y = F = 19кН.

M_x = M — F·z₂;

при z₂ = 0; M_x = 15кН·м.

при z₂ = 3м; M_x = -42кН·м.

Закрыть

sopromat.ueuo.com

Расчет балок онлайн. Примеры расчета

Расчет балки различается в зависимости от того, является она статически определимой, либо статически неопределимой. На сайте производится расчет любых балок, но подробное решение расписывается только для статически определимых балок, не имеющих промежуточных шарниров.

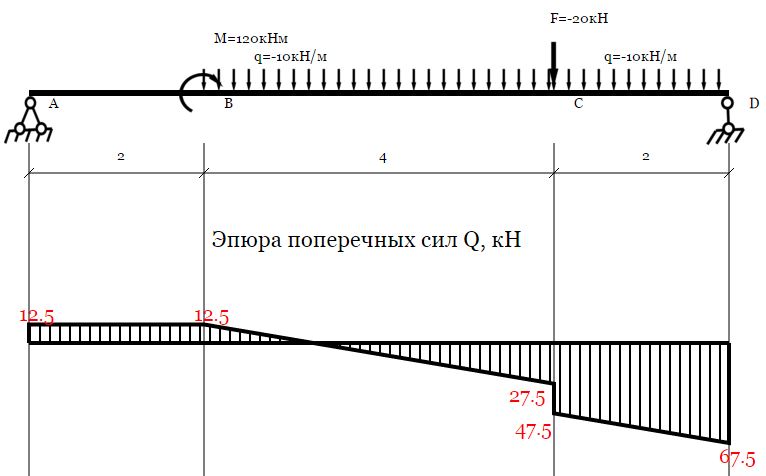
Балка на двух опорах. Построение эпюр

Для этого типа балок сервис позволяет определить и подробно расписывает:

• реакции опор
• эпюры поперечных сил и изгибающих моментов (эпюры Q и M)
• подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
• строятся эпюры нормальных и касательных напряжений
• по уравнениям метода начальных параметров вычисляются прогибы и углы поворота. Записываются и сами уравнения метода начальных параметров по участкам.

Посмотреть пример »

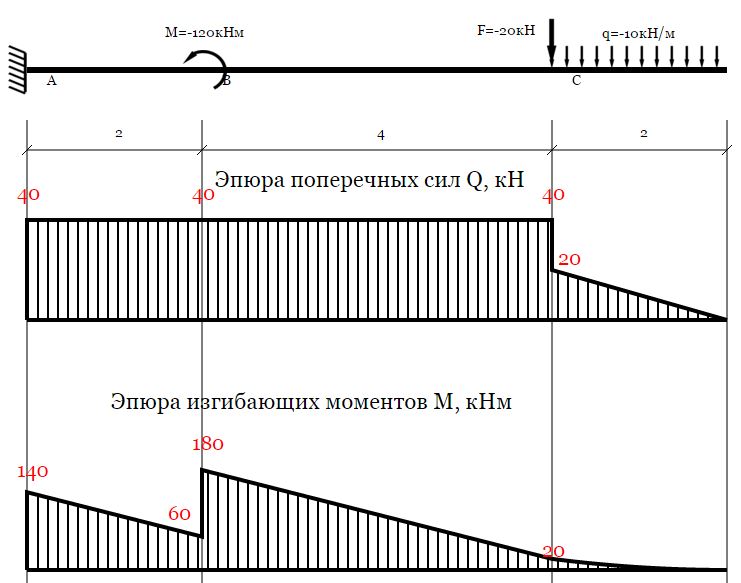
Консольная балка. Построение эпюр.

Для этого типа балок сервис позволяет определить и подробно расписывает:

• построение эпюр поперечных сил и изгибающих моментов
• подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
• строятся эпюры нормальных и касательных напряжений
• вычисляются прогибы и углы поворота.

Посмотреть пример »

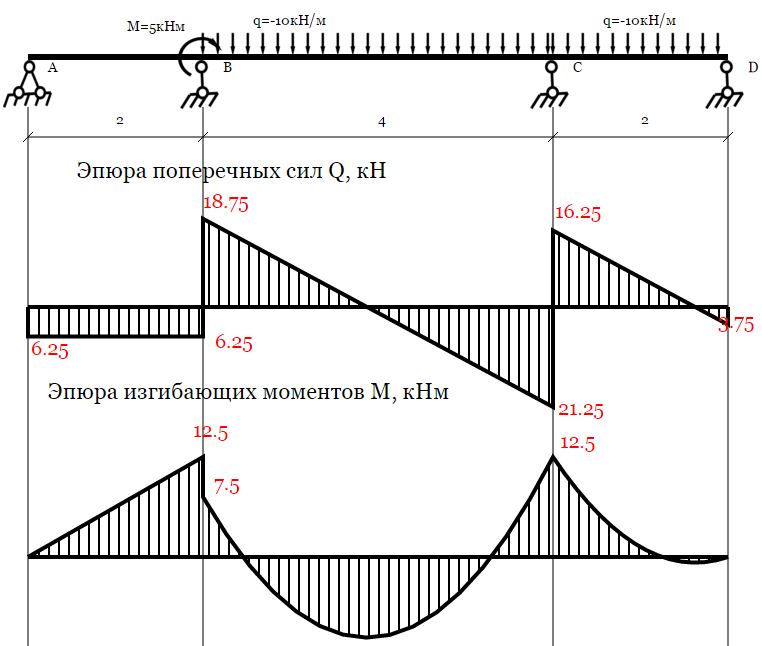
Статически неопределимая балка. Подбор сечения.

Для такого типа балок Вы можете получить

• только результаты расчета — (эпюры Q и M).

Естественно, по этим эпюрам можно легко найти реакции опор. Подробный ход расчета не расписывается, но, имея результаты, Вы легко можете проверить все промежуточные итоги своего расчета.

Посмотреть пример »

Балка с промежуточными шарнирами

Расчет балки с промежуточными шарнирами Вы должны производить, скорее всего, методом построения поэтажной схемы. Сервис, опять же, дает только конечный результат, но его наличие, естественно, очень упрощает проверку промежуточных этапов решения заданий.

Посмотреть пример »

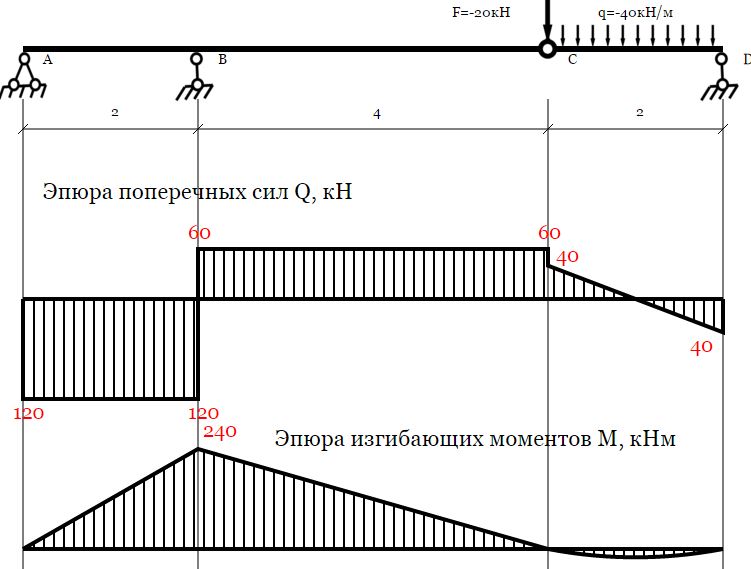
sopromat.xyz

Расчет балки

Подробный ход решения — расчет балки, построение эпюр

Заменим распределенную нагрузку равнодействующей

Q₁ = 6·2 = 12кН

Составим уравнения равновесия для определения реакций опор

Σ M_A = + P · 2 + M + Q1 · 3 — R_E · 6= + 12 · 2 + 8 + 12 · 3 — R_E · 6=0

Σ M_E = — P · 4 + M — Q1 · 3 + R_A · 6= — 12 · 4 + 8 — 12 · 3 + R_A · 6=0

Из этих уравнений находим реакции опор

R_A = 12.67кН.

R_E = 11.33кН.

Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений

На участке AB: (0 ≤ z₁ ≤ 2 м )

Q(z₁) = + R_A = + 12.67 = 12.667 кН

M(z₁) = + R_A · z = + 12.67 · z

M(0) = 0 кНм

M(2) = 25.333 кНм

На участке BC: (2 ≤ z₂ ≤ 4 м )

Q(z₂) = + R_A — P — q₁·(z — 2) = + 12.67 — 12 — 6·(z — 2)

Q(2) = 0.667 кН

Q(4) = -11.333 кН

M(z₂) = + R_A · z — P·(z — 2) — q₁·(z — 2)²/2 = + 12.67 · z — 12·(z — 2) — 6·(z — 2)²/2

M(2) = 25.333 кНм

M(4) = 14.667 кНм

Поскольку поперечная сила на участке пересекает ноль при z = 2.11 м, в этой точке будет экстремум на эпюре M

M(2.11) = 25.4 кНм

На участке CD: (4 ≤ z₃ ≤ 5 м )

Q(z₃) = + R_A — P — Q₁ = + 12.67 — 12 — 12 = -11.333 кН

M(z₃) = + R_A · z — P·(z — 2) — Q₁·(z — 3) = + 12.67 · z — 12·(z — 2) — 12·(z — 3)

M(4) = 14.667 кНм

M(5) = 3.333 кНм

На участке DE: (5 ≤ z₄ ≤ 6 м )

Q(z₄) = + R_A — P — Q₁ = + 12.67 — 12 — 12 = -11.333 кН

M(z₄) = + R_A · z — P·(z — 2) + M — Q₁·(z — 3) = + 12.67 · z — 12·(z — 2) + 8 — 12·(z — 3)

M(5) = 11.333 кНм

M(6) = 0 кНм

Максимальный момент в балке составляет M_max = 25.4 кНм. По этому значению подбираем сечение балки.

Условие прочности при изгибе σ = M_max / W ≤ [σ]

Отсюда, минимально необходимый момент сопротивления вычисляем по формуле W_min=M_max / [σ]

Понравились наши онлайн-расчетчики — поделитесь с друзьями   

sopromat.xyz