Прогиб консольной балки: Балки консольные — Прогибы при

Лабораторная работа № 9

ОПРЕДЕЛЕНИЕ ПРОГИБА И УГЛА ПОВОРОТА СЕЧЕНИЯ КОНСОЛЬНОЙ БАЛКИ ПРИ ПРЯМОМ ИЗГИБЕ

Цель работы: определить опытный путем величину прогиба и углов поворота сечения балки и сравнить их с величинами полученными путем теоретических расчетов.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Под воздействием внешних сил балка деформируется, ее продольная ось искривляется. Изогнутую часть балки называют упругой линией.

Деформация балки при изгибе характеризуется двумя величинами: прогибом У_х и углом поворота сечения q_х.

На рис.13 показана консольная балка, нагруженная на свободном конце сосредоточенной силой.

θ_x

Рис. 13.

Произведем теоретический расчет величин прогибов и углов поворота сечения при нагрузке Р.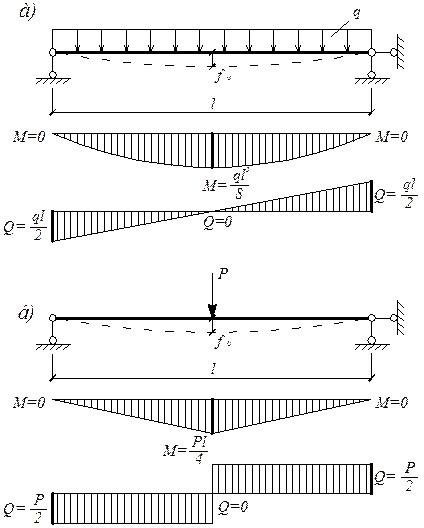

Для этого воспользуемся дифференциальным уравнением изогнутой оси балки.

y»Еj_z=M(x)

в нашем случае

y»Ej_z=-P(l-x)

Интегрируем дважды данное уравнение

Определим произвольные постоянные. Для этого рассмотрим опорное сечение: при х=0, у=0 и у’=0, откуда С=0 ; D=0 ;

Тогда

,

.

где у — прогиб в направлении, перпендикулярном к оси балки

х — расстояние сечения до заделки

Р — сила, приложенная к свободному концу

l — длина балки

E — модель упругости материала балки

I_z — осевой момент инерции поперечного сечения балки относи­тельно нейтральной оси

Приборы и оборудование

При исследовании изгиба консольной балки используется установка СМ-7Б, которая состоит из следующих составных частей: литого стола, к которому неподвижно прикреплен исследуемый образец, двух колонн, стяжки, гиревого подвеса и набора грузов.

Исследуемый образец представляет собой балку прямоугольного сечения размером ( 10 50 ) мм, выполненную из пружинной стали 60С2.

Вдоль балки перемещается подвеска, а также стержень для измерения углов поворотов. Подвеска и стержень могут быть зафиксированы при помощи винтов на исследуемой балке в любой точке ее длины.

Определение прогибов и углов поворота сечений образца производится с помощью индикаторов часового типа, которые крепятся в индикаторных стойках.

ПОРЯДОК ПРОВЕДЕНИЯ ИСПЫТАНИЙ.

1. Ознакомиться с установкой.

2. Произвести измерения поперечного сечения образца.

3. Установить индикаторы в местах в соответствии с выбранной схемой.

4. Подвесить гиревой подвес и записать начальные показания индикаторов.

5. Приложить расчетную нагрузку, добавляя его по 1,5 кг и отсчитывая показания по индикаторам.

Прогиб фиксируется непосредственно по шкале индикатора, а для определения угла поворота следует учесть, что перемещение стержня индикатора связано с углом поворота q и длиной рычага а.

Если S — перемещение измерительного стержня индикатора, то по причине малости углов ,

S=a q или

6. Испытание повторить 3 раза и вычислить среднее значение, которое принимается как расчётное.

7. Результаты испытаний занести в таблицу.

8. Вычислить теоретическое значение прогиба и угла поворота в принятом сечении.

9. Определить процент расхождения между величинами, полученными опытным путем и вычисленными теоретически по формулам :

;

Составление отчета

Должен содержать:

1. Эскиз балки с указанием размеров;

2. Таблицу с результатами измерений;

3. Теоретические вычисления прогибов и углов поворота;

4. Вычисление процента расхождения между опытными и теоретическими результатами.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется упругой линией балки, дифференциальное урав­нение упругой оси?

2. В чем заключаются деформации балок при изгибе?

3. Вычислить максимальный прогиб консольной балки с нагрузкой на конце.

4. Для этой же балки вычислить максимальный угол попорота попе­речного сечения.

5. Во сколько раз изменится прогиб балки, если нагрузку уменьшить в два раза?

Рис. 14. Варианты схемы опытов при испытании консольной балки

ОПРЕДЕЛЕНИЕ ПРОГИБА СТУПЕНЧАТОЙ БАЛКИ

Требуется определить прогиб свободного конца консольной бал­ки, состоящей из двух участков разной жесткости. Так как балка на отдельных участках имеет постоянную жесткость, можно исполь­зовать способ Мора Максвелла с применением правила Верещагина.

 

 

Рисунок 7.1

 

По правилу Верещагина искомый прогиб получается в результате «перемножения эпюр» по участкам:

Δ_E = Σ , (7. 1)

Здесь ω_P – площадь участка грузовой эпюры;

M_IC – ордината единичной эпюры под центром тяжести гру­зовой эпюры;

EJ – жесткость при изгибе па этом участке.

 

В отличие от балки постоянной жесткости разбивка на участки здесь определяется не только видом единичной эпюры, но еще и требованием постоянства жесткости на каждом участке. В нашем случае участков четыре: АВ, ЕС, CD и DE.

На рисунке 7.1 приведены грузовое и единичное состояние балки и построены соответствующие эпюры изгибающих моментов. Гру­зовая эпюра построена «расслоенной» – отдельно от каждой издействующих нагрузок (М и Р).

Жесткость на участке АС – 2EJ, на участке СЕ – EI.

Грузовая эпюра разбита на три части (площадь четвертой ча­сти – на участке DE – равна нулю).

Площади грузовых эпюр:

ω_P⁽¹⁾ = ·0,6²·P·ℓ² = 0,18 P·ℓ²,

ω_P⁽²⁾ = – 0,4·Pℓ·ℓ = – 0,4 P·ℓ²,

ω_P⁽³⁾ = – 0,4·Pℓ·0,6 ℓ = – 0,24 P·ℓ².

Соответствующие центрам тяжести этих площадей ординаты единичной эпюры:

M_IC1 = – 1,8 ℓ;

M_IC2 = – 1,5 ℓ;

M_IC1 = – 0,7 ℓ.

Итак,

Δ_E = Σ = + + + = (–0,162 + 0,300 + 0,168) = 0,306

 

ЛИТЕРАТУРА

1. Дарков А. В., Шпиро Г. С.Сопротивление материалов, М., 1965 и 1975 гг.

2. СмирновА. Ф.и др. Сопротивление материалов, 1975.

3. Феодосьев В. И.Сопротивление материалов, М., 1974.

4. Беляев Н. М.Сопротивление материалов, М., 1976.

5.Сборник задач по сопротивлению материалов под редакцией В. К. Качурина, М., 1972.

6. УманскийА. А.Сборник задач по сопротивлению материалов, М., 1973

7Миролюбов И. Н. и др.Пособие к решению задач по сопротивлению материалов, М., 1962.

8. Писаренко Г. С. и др.Справочник по сопротивлению материалов, Киев, 1975.

9. Любошиц М. И., Ицкович Г.М. Справочник по сопротивлению мате­риалов, Минск, 1969.

СОДЕРЖАНИЕ

 

1. К ЗАДАЧЕ № 1 СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ ШАР­НИРНО — СТЕРЖНЕВАЯ СИСТЕМА ………………………………………………………………………….. 3

1.1. Выражение усилии и напряжений в стержнях через силу Q. …. 3

1.2. Определение грузоподъемности системы по способу допускаемых напряжений 6

1.3. Определение грузоподъемности системы по способу допускаемых нагрузок 7

1.4. Сравнение результатов………………………………………………………….. 7

2. .. К ЗАДАЧЕ № 2. СТАТИЧЕСКИ НЕОПРЕДЕ­ЛИМАЯ СТЕРЖНЕВАЯ СИСТЕМА 8

2.1 Определение величины сил H₀ и 3·H₀, при которых зазор закроется…………………. 9

2. 2. Определение реакции основания в нижнем сечении среднего стержня при H = 100 кН (10 тс). 11

2.3 Определение усилий и напряжений в крайних стержнях при заданной величине сил . 15

2.4 Установим, на сколько градусов надо охладить средний стержень, чтобы реакция основания в нижнем сечении среднего стержня при заданных силах обратилась в нуль 16

3. .. К ЗАДАЧЕ №3. КРУЧЕНИЕ СТЕРЖНЯ КРУГЛО­ГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 17

3.1 Определение неизвестного момента X (М_к)………………………….. 17

3.2 Построение эпюры крутящих моментов……………………………….. 19

3.3 Определение диаметра вала………………………………………………….. 19

3.4 Построение эпюры углов закручивания……………………………….. 21

4. .. К ЗАДАЧЕ № 4. ГЕОМЕТРИЧЕСКИЕ ХАРАК­ТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ 22

4.1 Определение положения центра тяжести. ……………………………… 25

4.2 Определение моментов инерции относительно центральных осей X и Y 26

4.3 Определение величин главных центральных моментов инерции ……………………. 26

4.4 Определение направления главных центральных осей…………. 27

5. К ЗАДАЧЕ № 5. СТАТИЧЕСКИ ОПРЕДЕЛИМАЯ БАЛКА27

5.1 Пример «а»………………………………………………………………………… 29

5.2 Пример «б»……………………………………………………………………….. 33

6. К ЗАДАЧЕ № 6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ ВАЛКА. 38

7. К ЗАДАЧЕ № 7. ОПРЕДЕЛЕНИЕ ПРОГИБА СТУПЕН­ЧАТОЙ БАЛКИ 47

ЛИТЕРАТУРА…………………………………………………………………….. 49

 

ГАНЕЛИН ИОСИФ НАУМОВИЧ

 

ЗАХАРОВ ВЯЧЕСЛАВ МИХАЙЛОВИЧ

 

 

СТРОИТЕЛЬНАЯ МЕХАНИКА

 

 

М Е Т О Д И Ч Е С К И Е У К А З А Н И Я

 

к выполнению контрольных работ по сопротивлению материалов для студентов заочной формы обучения строительных специальностей.

Часть1. Простые деформации

 

Объем 2,6 Тираж 25 Заказ ….. Бесплатно Формат A1

Брянская государственная инженерно-технологическая академия. 241037 г. Брянск, ул. Станке Димитрова, 3, редакционно-издательский отдел.

 

 

Отпечатано: лаборатория кафедры «Сопротивление материалов и строительная механика» БГИТА.

 

 

---

Выбор начала координат балки — Теория и решение задач

При составлении универсальных уравнений метода начальных параметров (МНП) за начало координат (НК) выбирается крайнее левое либо правое сечение балки при этом желательно, что бы оно располагалось на опоре.

Эта рекомендация несколько упрощает последующие расчеты. Дело в том, что на опорах некоторые перемещения отсутствуют, следовательно, соответствующие начальные параметры (угол наклона сечения θ₀ и прогиб y₀ балки в начале координат) будут равны нулю.

Рассмотрим это на следующих примерах:

Консольная балка

В жесткой заделке консольной балки исключены любые перемещения сечений.

Поэтому в случае выбора начала координат на опоре оба начальных параметра равны нулю, в то время как при выборе за НК противоположного сечения возникнет необходимость дополнительных расчетов углового перемещения и прогиба балки в начале координат.

Балка на шарнирных опорах

В шарнирно-неподвижных опорах исключены только линейные перемещения, поэтому в случае выбора на данной схеме НК справа (на опоре) нулю будет равен только прогиб балки в начале координат.

Балка без крайних опор

В данном случае оба крайних сечения балки могут иметь как линейные, так и угловые перемещения, поэтому при выборе начала координат балки рекомендуем обратить внимание на положение распределенной нагрузки.

Если ее действие начинается от одного из крайних сечений, то за НК следует принять противоположное ему (в этом случае не придется продлевать и добавлять компенсирующую распределенную нагрузку).

В других случаях в качестве начала координат для уравнений МНП можно выбирать любое из крайних сечений балки.

Пример расчета методом начальных параметров >
Краткая теория по сопромату >
Примеры решения задач >

Определить угол поворота и прогиб сечения В консольной балки

Пример задачи 5.15

Определить угол поворота и прогиб сечения В консольной балки (в долях от жесткости сечения

), рис. 5.28.

Решение

Эпюра изгибающих моментов от заданной нагрузки (грузовая эпюра

) показана на рис. 5.28, а.

Для определения прогиба в сечении В к свободной от заданной нагрузки балке (вспомогательное состояние) в названном сечении прикладывается вспомогательная единичная сосредоточенная сила (F = 1) и строится эпюра изгибающих моментов — единичная эпюра

(рис. 5.28, б). Единичная сила направляется произвольно, т. е. в положительном или отрицательном направлении оси У.

Аналогичная операция производится для определения угла поворота сечения. Только в качестве вспомогательной единичной силы выступает единичный вспомогательный момент (М = 1), направляемый произвольно относительно оси X. Эпюра от единичного момента

показана на рис. 5.28, в.

На рис. 5.28, б и в схема балки и единичные эпюры совмещены. Заметим, что балка имеет один расчетный участок как для

,

так для

и что единичные эпюры прямолинейны и имеют вид треугольника или прямоугольника, а грузовая — криволинейна и имеет сложное очертание.

Для определения перемещений по способу Верещагина используются эпюры изгибающих моментов (грузовые и единичные). От одних из них берутся площади эпюр (

), из других — ординаты (у) под центром тяжести первых. Поскольку грузовая эпюра имеет криволинейное очертание, площадь должна браться с этой эпюры.

Для проведения расчета эпюра

сложного очертания делится на простые фигуры: прямоугольник (от момента М) площадью

и параболический треугольник (от нагрузки q) площадью

На выделенных простых фигурах отмечаются их центры тяжести (см. табл. 5.1).

На единичных эпюрах отмечаются ординаты у, лежащие под центром тяжести составляющих частей грузовой эпюры

. В данном примере ордината определяется как

Для определения углов поворота сечений ординаты берутся из единичной эпюры

:

Прогиб в сечении В по формуле (5.12):

Все слагаемые в выражении прогибов положительны, так как площади

и ординаты у лежат по одну сторону от оси эпюры. Положительные значения означают, что прогиб происходит в направлении единичной силы, т. е. вниз.

Угол поворота сечения В

В полученном выражении слагаемые отрицательны, так как площади

и ординаты у лежат по разную сторону от оси эпюры. Отрицательное значение означает, что поворот сечения происходит в направлении, противоположном направлению единичного момента, т. е. по ходу часовой стрелки (рис. 5.28, г).

Эпюра прогибов показана на рис. 5.28, г.

Таким образом, перемещения на свободном конце балки (в долях от жесткости сечения)

(по ходу часовой стрелки), (вниз).

Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:

Примеры решения задач по сопротивлению материалов

Дополнительные задачи которые вам будут полезны:

Расчет балки онлайн с расчетом на прочность и построение эпюр онлайн с решением. —  

Расчет балки

Подробный ход решения — расчет балки, построение эпюр

Заменим распределенную нагрузку равнодействующей

Q₁ = 6·2 = 12кН

Составим
уравнения равновесия для определения реакций опор

Σ M_A = + P · 2 + M + Q1 · 3 — R_E · 6= + 12 · 2 + 8 + 12 · 3 — R_E · 6=0

Σ M_E = — P · 4 + M — Q1 · 3 + R_A · 6= — 12 · 4 + 8 — 12 · 3 + R_A · 6=0

Из этих уравнений находим реакции опор

R_A = 12. 67кН.

R_E = 11.33кН.

Записываем уравнения поперечных сил и изгибающих моментов на
участках балки
, используя метод сечений

На участке AB: (0 ≤ z₁ ≤ 2 м )

Q(z₁) = + R_A = + 12.67 = 12.667 кН

M(z₁) = + R_A · z = + 12.67 · z

M(0) = 0 кНм

M(2) = 25.333 кНм

На участке BC: (2 ≤ z₂ ≤ 4 м )

Q(z₂) = + R_A — P — q₁·(z — 2) = + 12. 67 — 12 — 6·(z — 2)

Q(2) = 0.667 кН

Q(4) = -11.333 кН

M(z₂) = + R_A · z — P·(z — 2) — q₁·(z — 2)²/2 = + 12.67 · z — 12·(z — 2) — 6·(z — 2)²/2

M(2) = 25.333 кНм

M(4) = 14.667 кНм

Поскольку поперечная сила на участке пересекает ноль при z = 2.11 м, в этой точке будет экстремум на эпюре M

M(2.11) = 25.4 кНм

На участке CD: (4 ≤ z₃ ≤ 5 м )

Q(z₃) = + R_A — P — Q₁ = + 12. 67 — 12 — 12 = -11.333 кН

M(z₃) = + R_A · z — P·(z — 2) — Q₁·(z — 3) = + 12.67 · z — 12·(z — 2) — 12·(z — 3)

M(4) = 14.667 кНм

M(5) = 3.333 кНм

На участке DE: (5 ≤ z₄ ≤ 6 м )

Q(z₄) = + R_A — P — Q₁ = + 12.67 — 12 — 12 = -11.333 кН

M(z₄) = + R_A · z — P·(z — 2) + M — Q₁·(z — 3) = + 12.67 · z — 12·(z — 2) + 8 — 12·(z — 3)

M(5) = 11. 333 кНм

M(6) = 0 кНм

Максимальный момент в балке составляет M_max = 25.4 кНм. По этому значению
подбираем сечение балки.

Условие прочности при изгибе σ = M_max / W ≤ [σ]

Отсюда, минимально необходимый момент сопротивления вычисляем по формуле W_min=M_max / [σ]

Расчет опорных реакций балки на двух опорах онлайн

Расчет выполняется по следующей методике:

1. Заменяем распределенную нагрузку ее равнодействующей, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка L, на котором она действует: Fq = q*L.

2. Обозначаем опоры. Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно-неподвижную и одну шарнирно-подвижную опоры.

3. Освобождаемся от опор и заменяем их действие на балку реакциями.

Реакции опор при такой нагрузке будут только вертикальными.

4. Составляем уравнения равновесия вида:
M_A = 0; M_B = 0,

Моментом силы относительно точки называется произведение этой силы на плечо — кратчайшее расстояние от этой точки приложения силы (в общем случае — до линии действия силы).

5. Выполним проверку решения. Для этого составим уравнение равновесия:
Y = 0,

Если оно удовлетворено, то реакции найдены правильно, а если нет, но в решении допущена ошибка.

6. Строим эпюру поперечных сил Q_x. Для этого определяем значения поперечных сил в характерных точках.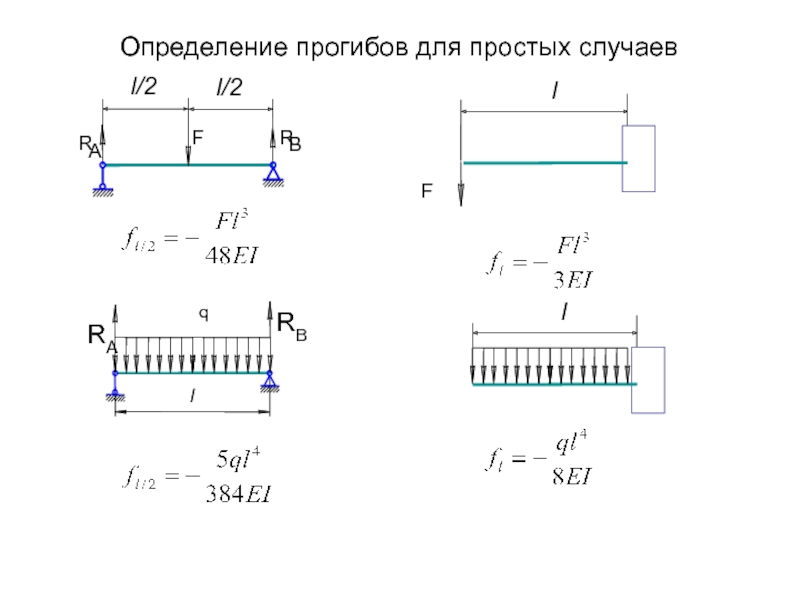 Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот.

В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно Q_лев и Q_прав.

Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правилам:

а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии;

б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.

Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Q_x.

7. Строим эпюру изгибающих моментов М_x. Для этого определяем изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против — отрицательным (со знаком «минус»), а для правой части наоборот.

В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее. Изгибающие моменты в этих точках обозначаются соответственно М_лев и М_прав. В точках приложения сил определяется одно значение изгибающего момента.

Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами:

а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией;

б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.

Пример решения балки:

Построение эпюр усилий онлайн

Інструкція.

Программа позволяет определить опорные реакции и построить эпюры внутренних усилий для двухопорной и консольной балки.

Дальнейшие инструкции будут приведены на примере балки на двух опорах.

1. Выберите условия крепления концов балки. Возможны варианты — свободный, шарнир и жесткое. В нашем примере левый и правый конец стержня не имеют креплений, поэтому выбираем вариант «свободный».

Если по ошибке был выбран другой вариант, нажимаем на кнопку «Новая схема».

2. Указываем длину балки и координаты опор. Длина балки равна «13», а координаты опор от левого конца балки, в соответствии к опоры A — «2» и к опоре B — «11».

3. Указываем нагрузку.
Выбираем количество сосредоточенных моментов — «2». В таблице вводим значения моментов и их координаты от левого конца балки. M₁=40, a₁=6 и M₂=-20, a₂=13
(момент который вращается против часовой стрелки — положительный, по — отрицательный).
Выбираем количество сосредоточенных сил — «2». В таблице вводим значение сил и их координаты. F₁=9, b₁=0
и F₂=6. 93, b₂=9 (сила направленная вниз — положительная, вверх — отрицательная).
Выбираем количество равномерно распределенной нагрузки — «1». В таблице вводим значение РРН, координаты начала
и конца РРН. q₁=12, c₁=2 та d₁=8 (РРН направлена вниз — положительная, вверх — отрицательная).

4. Нажимаем на кнопку «Построить эпюры». После нажатия определяются опорные реакции и строятся эпюры усилий. Если нужно определить усилия в произвольном сечении, введите координату в форму. Если нужно, задайте точность
расчета и выберите правое или левое сечение.

Скриншот к примеру:

Скриншот к примеру (эпюра поперечных сил):

Скриншот к примеру (эпюра изгибающих моментов):

Онлайн расчет статически неопределенной балки

Расчет выполняется методом сил

Канонические уравнения метода сил:

Где коэффициенты системы определяются:

Принцип ввода данных, рассмотрим с помощью следующего примера:

1. Задание длины (12м) и условий закрепления стержня. Левый конец стержня свободен, а правый — жестко закрепленный. Задаем координаты опор (отсчет ведется от левого конца стержння). Первая опора имеет координату 2м, вторая — 7м.

2. Задаем нагрузки, использовав соответствующие правила знаков:

3. В случае, если жесткость балки переменная, задайте необходимые пропорции (нажмите на кнопку «Изменить жесткость»):

4. Для начала расчета нажмите на кнопку «Построить эпюры».

Для расчета балок используется следующая основная система (ОС). Выбрать ОС невозможно.

Решение системы уравнений:

Опорные реакции:

Расчет онлайн для разнотипных балочных конструкций.

Строительство зданий – сложная работа, требующая точных расчетов и качественного выполнения работы. Основным материалом в строительстве жилых домов является древесина. Несущие конструкции изготавливаются из этого материала. Рассмотрим способы расчета балки онлайн.

Разновидности перекрытий

Назначение:

1. Межэтажные.
   Прочное, надежное перекрытие. Между двумя материалами складываются звуко- и теплоизоляционные наполнители.
2. Чердачное.
   Является частью стропильной конструкции крыши. Чердак оборудован изоляцией от шума и пара.
3. Цокольное.
   Выносят высокие нагрузки. Делаются с теплоизоляцией.

Балки бывают двух видов:

1. цельные;
2. клееные.

Слабым звеном монолитных балок является ограниченная длина. Не могут быть больше 5 метров.

Преимуществами клееных балок над цельными являются:

• перекрытие больших пролетов;
• легкость установки;
• маленькая масса;
• длительная эксплуатация;
• пожароустойчивые;
• не деформируются.

Каким образом определяется длина балки?

Обычно размещаются параллельно самой маленькой стене. Размеры зависят от материалов, из которых изготавливаются блоки и от общего объема материала. Для крепления используют металлические крепежи (кронштейны, уголки, пластинки с перфорацией, плитки). Если применяете один из этих видов крепежа, то длина балки должна соответствовать пролету комнаты.

Также балки могут быть частью стропильных элементов. Конструкция опирается на мауэрлат. Данный способ увеличивает длину исходного материала на метр.

Советы для правильного расчета:

1. Учитывайте глубину введения материалов в стену. Глубина вхождения для стен из кирпича составляет от 150 мм для балок из бруса и 100 мм для досок. В домах из дерева – от 70 мм.
2. Длина балки составляет минимум 6 м.

Инструкция для подсчета:

1. замерьте пролет;
2. выберите закрепляющие элементы;
3. рассчитайте влияющую нагрузку;
4. подберите шаг и сечение.

При строительстве можно выпустить балки наружу на 31- 60 см. Таким образом, формируется свес крыши.

Определение действующей нагрузки

В жилом помещении имеется два дверных пролета. Обычно отличаются по размерам, но в квадратной комнате могут быть одинаковыми.

Перемычки укладывают в более коротком проеме ,длиной 3-4 метра. По стандарту, стороны должны соотноситься в пропорции семь к пяти. Так исключается деформация. Если не соблюдать этих пропорций, балки прогнутся. Возможный деформация – два см на четыре метра.

Для устранения провисания бруса, изготовьте снизу на несколько см, при этом придав форму арки.

Прогиб можно рассчитать по формуле f(нор)= L/200

L –длина пролета,

200 – расстояние на единицу погружения дерева.

Нагрузка на любую конструкцию определяется по нескольким формулам.

Первая – геометрическая характеристика сечения стержнями:

W≥M/R . M – время относительно нейтральной оси сечения балки или другого твердого тела,

R – рассчитываемое сопротивление, которое нужно взять из справочника исходя из основы.

Для стержней прямоугольной формы формула выглядит так:

W_Z =b∙ h 2/6,

b – ширина балки,

h – высота.

Перекрытие во многих случаях является кровлей и полом следующего и предшествующего этажей. Объединяйте, учитывая нагрузку мебели на поверхности. Если неправильно распределить, появляется риск разрушения конструкций. Не следует применять уж очень широкий шаг промеж балками и отказываться от лагов. Учитывайте, что пространство между основами зависит от толщины досок. Если имеются лаги, то расстояние посередине должно составлять метр.

Совет! Предусмотрите массу утеплителя. Цокольное перекрытие, длиной 1 м2, весит 100 килограммов. Увеличивает вдвое одну и ту же массу опилкобетон. Керамзит еще тяжелее.

Выяснение сечения и шага балки

1. Параметры балок строго регламентированы. Так, соразмерность – 1:1:4. Широта – с 5 до 21 сантиметра, высота – от 10 до 31 сантиметра. Учитывайте утеплитель! Бревна перекрытия должны иметь диаметр от 11 до 31 сантиметра.
2. Установочный шаг – примерно 30–120 сантиметров. При каркасном строении шаг соответствует дистанции промеж твердыми основами.

Требования, предъявляемые к конструкциям:

• влагосодержание материала – максимум 15%;
• нельзя использовать испорченную древесину, то есть синюшную, поражённую грибком, насекомыми, грызунами;
• обработка антисептическим составом;
• размерное отношение – 7:5 для брусьев;
• чем больше высота лаг, тем больше нагрузка, выдерживаемая балкой;
• для ровного перекрытия сделайте подъем ярусов;
• брусья и бревна замените досками, уложенными на ребро, если укладка интенсивная.

Онлайн калькулятор для расчета деревянных балок

Высота балки (мм)
Ширина балки (мм)
Материал древесины
Пролет (м)
Шаг балок (м)

Произвести расчет балки возможно самостоятельно: рассчитать нагрузки, воздействующие на перекрытие по формулам и параметрам или воспользоваться онлайн калькулятором. Также можно выбрать подходящую конструкцию, исходя из имеющихся условий.

Бесплатный Калькулятор Луча | Изгибающий момент, Калькулятор поперечной силы и прогиба

Добро пожаловать в наш бесплатный онлайн калькулятор изгибающего момента и диаграммы силы сдвига, который может генерировать реакции, Диаграммы силы сдвига (SFD) и диаграммы изгибающих моментов (BMD) консольной балки или опертой балки. Используйте этот калькулятор балок, чтобы определить реакции на опорах, нарисуйте диаграмму сдвига и момента для балки и рассчитайте прогиб стали или дерево луч. Бесплатный онлайн лучевой калькулятор для генерации реакций, расчет прогиба стальной или деревянной балки, составление диаграмм сдвига и момента для балки. Это бесплатная версия нашей полной SkyCiv. Beam Software. Доступ к нему можно получить в любом из наших Платные аккаунты, который также включает программное обеспечение для полного структурного анализа.

Используйте интерактивную рамку выше для просмотра и удаления длины луча, поддерживает и добавляет нагрузки. Любые сделанные изменения автоматически перерисовывают диаграмму свободного тела любым простым или консольным лучом.. Калькулятор реакции луча и расчеты изгибающего момента будут запущены, как только «Решить» нажата кнопка и автоматически сгенерирует диаграммы моментов сдвига и изгиба. Вы также можете нажать отдельные элементы этого калькулятора луча LVL, чтобы редактировать модель.

Калькулятор пролета луча легко рассчитает реакции на опорах. Умеет рассчитывать реакции на опорах для консольных или простых балок.. Это включает в себя расчет реакций для балки кантилевера, который имеет реакцию изгибающего момента, а также х,у сил реакции.

Вышеуказанный калькулятор балок со стальной балкой — это универсальный инструмент для расчета конструкций, используемый для расчета изгибающего момента в алюминии., деревянная или стальная балка. Его также можно использовать в качестве калькулятора грузоподъемности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Может вместить до 2 различные сосредоточенные точечные нагрузки, 2 распределенные нагрузки и 2 моменты. Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками. (UDL), треугольные распределенные нагрузки или трапециевидные распределенные нагрузки. Все нагрузки и моменты могут иметь как восходящее, так и нисходящее направление по величине., которые должны быть в состоянии учитывать наиболее распространенные ситуации анализа пучка. Расчет изгибающего момента и силы сдвига может занять до 10 секунд, чтобы появиться и, пожалуйста, обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, Диаграмма силы сдвига и диаграмма изгибающего момента балки.

Одна из самых мощных функций использует его в качестве калькулятора отклонения луча (или калькулятор смещения луча). Это может быть использовано для наблюдения расчетного отклонения балки с простой опорой или балки кантилевера. Возможность добавлять формы и материалы раздела, это делает его полезным в качестве калькулятора для деревянных балок или в качестве калькулятора для стальных балок для LVL-лучей или I-лучевой конструкции. На данный момент, эта функциональность доступна в SkyCiv Beam который имеет гораздо больше функциональных возможностей для древесины, конструкция из бетона и стальных балок.

SkyCiv предлагает широкий спектр программного обеспечения для анализа и проектирования облачных вычислений для инженеров. Как постоянно развивающаяся технологическая компания, мы стремимся к инновациям и стимулированию существующих рабочих процессов, чтобы сэкономить время инженеров в их рабочих процессах и проектах.

Расчет балки на прогиб — онлайн калькулятор

Онлайн калькулятор по определению прогиба балки.

Для расчета вам необходимо:


1. Выбрать форму поперечного сечения

2. Выбрать материал (при использовании металлических балок — можно использовать сортамент)

3. Выбрать необходимую расчетную схему

4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)

5. Указать геометрические размеры, указанные на картинках

6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)

Из возможных поперечных сечений в данном онлайн калькуляторе выбраны само часто встречающиеся сечения: круг, труба, двутавр, швеллер, уголок, прямоугольник, квадрат и профильная труба.

В расчет входят такие материалы как дерево, сталь, железобетон, алюминий, медь и стекло.

Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка и заделка-свободный конец.

После того, как прогиб балки рассчитается – появится кнопка Подробнее, нажав на которую, можно узнать площадь сечения рассчитываемого элемента, его массу, распределенную нагрузку от собственного веса и момент инерции заданного сечения).

Зная значение длины пролета балки по СП 20.13330.2016 «Нагрузки и воздействия» для таких конструкций как балка, ферма, ригель, прогон, плита, настил покрытий и перекрытий, рассчитывается предельный прогиб, который можно сравнить с получившимся прогибом и принять решение о сечении вашей конструкции (для уменьшения прогиба в 1-ую очередь надо увеличивать высоту сечения).

При расчете балки программа уже учитывает собственный вес.

Помимо того, что Вы рассчитаете балку на прогиб, нужно ее проверить и на прочность здесь .

Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие
строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.

Последние изменения:

— Добавлен расчет предельного прогиба балки

— Добавлена возможность загружения балки сосредоточенной силой

— Исправлены графические замечания с расположением швеллера

— Добавлен расчет таврого сечения

— Исправлено положение прямоугольного сечения

— Добавлена возможность поворота швеллера

— Добавлена возможность ввода своих значений модуля упругости и плотности материала

— Исправлено отображение толщины стенки и полки швеллера

Калькулятор отклонения балки

КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ УЧАСТНИКОВ
Калькулятор	Определение
	Расчет элементов сжатия (продольного изгиба)
ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГНОЗА
	Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами
	Балка с простой опорой и сосредоточенной нагрузкой в ​​любой точке
	Просто поддерживаемая балка с двумя Точечные нагрузки
	Балка с простой опорой и частично распределенной промежуточной нагрузкой
	Балка с простой опорой и двумя частично распределенными промежуточными нагрузками
	Балка с простой опорой и моментом
	Балка с простой опорой и двумя моментами
КАНТИЛЬВЕРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГНОЗА
	Консольная балка с множественными точечными / распределенными нагрузками и моментами
	Консольная балка с одинарной нагрузкой
	Распределенная нагрузка консольной балки
	Консольная балка с одним моментом
КАЛЬКУЛЯТОРЫ ПРОБЕГА ФИКСИРОВАННОЙ ЛУЧИ
	Фиксированный -Фиксированная балка с множественными точечными / распределенными нагрузками и моментами
	Фиксированная — фиксированная балка с одинарной нагрузкой
	Фиксированный — Неподвижная балка с распределенной нагрузкой
	Фиксированная — фиксированная балка с одним моментом

Калькулятор отклонения балки

Этот калькулятор отклонения балки поможет вам определить максимальное отклонение балки для балок с простой опорой и консольных балок, несущих простых конфигураций нагрузки . Вы можете выбрать один из нескольких типов нагрузки, которые могут воздействовать на балку любой длины по вашему желанию. Величина и расположение этих нагрузок влияют на то, насколько балка изгибается. В этом калькуляторе отклонения балки вы узнаете о различных формулах отклонения балки , используемых для расчета отклонений балок с жесткой опорой и балок консольных балок. Вы также узнаете, как модуль упругости балки и момент инерции ее поперечного сечения влияют на расчетный максимальный прогиб балки.

Что такое прогиб балки и изгиб балки

В строительстве мы обычно используем каркасные конструкции , которые удерживаются на месте фундаментом в земле. Эти каркасные конструкции подобны каркасам зданий, домов и даже мостов. В кадре мы называем вертикальное обрамление колонн , а горизонтальные балки . Балки — это длинные элементы конструкции, которые несут нагрузки, создаваемые горизонтальными плитами конструкций, включая перекрытия и крыши.

Когда балки несут слишком тяжелые для них нагрузки, они начинают гнуться. Мы называем величину изгиба балки , прогиб балки . Отклонение балки — это вертикальное смещение точки вдоль центра тяжести балки. Мы также можем рассматривать поверхность балки как опорную точку, если нет изменений в высоте или глубине балки во время изгиба.

Как рассчитать максимальный прогиб балки

Мы снабдили наш калькулятор прогиба балки формулами, которые инженеры и студенты-инженеры используют для быстрого определения максимального прогиба, который будет испытывать конкретная балка из-за нагрузки, которую она несет.Однако эти формулы могут решать только простые нагрузки и их комбинацию. Мы составили для вас таблицы этих формул, как показано ниже:

Формулы прогиба балок без опоры

Формулы отклонения консольной балки

Метод наложения

Для расчета максимального прогиба балки с комбинацией нагрузок мы можем использовать метод наложения . Метод наложения утверждает, что мы можем приблизительно оценить полное отклонение балки, сложив вместе все отклонения, вызванные каждой конфигурацией нагрузки.Однако этот метод дает нам лишь приблизительное значение фактического максимального прогиба. Расчет сложных нагрузок потребует от нас использования так называемого метода двойного интегрирования .

Жесткость балки

Для расчета прогиба балки необходимо знать жесткость балки и величину силы или нагрузки, которые могут повлиять на изгиб балки. Мы можем определить жесткость балки, умножив модуль упругости балки , E , на ее момент инерции , I .Модуль упругости зависит от материала балки. Чем выше модуль упругости материала, тем больше прогиб может выдержать огромные нагрузки, прежде чем достигнет предела разрушения. Модуль упругости бетона составляет 15-50 ГПа (гигапаскалей), а у стали — около 200 ГПа и выше. Эта разница в значениях модуля упругости показывает, что бетон может выдерживать лишь небольшой прогиб и трескается быстрее, чем сталь.

Вы можете узнать больше о модуле упругости, воспользовавшись нашим калькулятором напряжений.С другой стороны, чтобы определить момент инерции для определенного поперечного сечения балки, вы можете воспользоваться нашим калькулятором момента инерции. Момент инерции представляет собой величину сопротивления материала вращательному движению. Момент инерции зависит от размеров поперечного сечения материала.

Момент инерции также зависит от оси вращения материала. Чтобы лучше понять эту концепцию, давайте рассмотрим поперечное сечение прямоугольной балки шириной 20 см и высотой 30 см.Используя формулы, которые вы также можете увидеть в нашем калькуляторе момента инерции, мы можем вычислить значения момента инерции этого поперечного сечения следующим образом:

Iₓ = ширина * высота³ / 12
= 20 * (30³) / 12
= 45000 см⁴

Iᵧ = высота * ширина³ / 12
= 30 * (20³) / 12
= 20,000 см⁴

Обратите внимание на два значения момента инерции. Это потому, что мы можем рассматривать изгиб балки по вертикали (по оси x, то есть Iₓ) или по горизонтали (по оси y, то есть Iᵧ).Поскольку мы учитываем отклонение балки при вертикальном изгибе, для расчетов всегда нужно использовать Iₓ . Полученные нами значения говорят нам о том, что балку труднее изгибать при вертикальной нагрузке и легче изгибать при горизонтальной нагрузке. Эта разница в значениях момента инерции является причиной того, что мы видим балки в этой конфигурации, в которой ее высота больше, чем ее ширина.

Понимание формул прогиба балки

Теперь, когда мы знаем концепции модуля упругости и момента инерции, мы можем теперь понять, почему эти переменные являются знаменателями в наших формулах отклонения балки.Формулы показывают, что чем жестче балка, тем меньше будет ее прогиб. Однако, изучив наши формулы, мы также можем сказать, что длина балки также напрямую влияет на прогиб балки. Чем длиннее балка, тем больше она может изгибаться и тем больше может быть прогиб.

С другой стороны, нагрузки

влияют на отклонение балки двумя способами: направление отклонения и величина отклонения . Нисходящие нагрузки склонны отклонять балку вниз.Нагрузки могут быть в виде точечной нагрузки, линейного давления или моментной нагрузки. Формулы в этом калькуляторе ориентированы только на нисходящие или восходящие направления для точечной нагрузки и распределенных нагрузок. Распределенные нагрузки аналогичны давлению, но учитывают только длину балки, а не ширину балки. Формулы в этом калькуляторе также учитывают момент или крутящий момент нагрузки как по часовой стрелке, так и против часовой стрелки. Просто проконсультируйтесь по направлениям стрелок на соответствующем изображении формулы, чтобы выяснить, в каком направлении имеется положительное значение нагрузки.

Пример расчета прогиба балки

Для примера расчета прогиба балки рассмотрим простую деревянную скамью с ножками на расстоянии 1,5 метра друг от друга в их центрах. Допустим, у нас есть доска из восточной белой сосны толщиной 4 см и шириной 30 см, которая служит сиденьем для этой скамейки. Мы можем рассматривать это сиденье как балку, которая отклоняется, когда кто-то садится на скамейку. Зная размеры этого сиденья, мы можем вычислить его момент инерции, как в нашем примере выше.Поскольку нам нужно рассчитать Iₓ, его момент инерции будет:

Iₓ = ширина * высота³ / 12
= 30 * (4³) / 12
= 160,0 см⁴ или 1,6x10⁻⁶ м⁴

Сосна восточная белая имеет модуль упругости 6800 МПа (6,8x10⁹ Па) , что является значением, которое мы получили из Справочника по древесине. Вы также можете легко получить значение модуля упругости для других материалов, таких как сталь и бетон, в Интернете или в местной библиотеке.Теперь, когда мы знаем эти значения, давайте рассмотрим нагрузку, которую будет нести этот стенд. Предположим, что ребенок 400 N сидит в центре скамейки. Теперь мы можем рассчитать прогиб сиденья скамейки из-за точечной нагрузки в его центре:

δₘₐₓ = P * L³ / (48 * E * I)
δₘₐₓ = (400 Н) * (1,5 м) ³ / (48 * 6,8x10⁹ Па * 1,6x10⁻⁶ м⁴)
δₘₐₓ = 0,002585 m = 2,5850 мм

Это означает, что многоместное сиденье прогнется примерно на 2.6 миллиметров на от исходного положения, когда ребенок сидит посередине скамейки.

Если вы нашли эту тему интересной и хотели бы узнать больше о прочности материалов, вам также может понравиться наш калькулятор запаса прочности. Вы также можете воспользоваться нашим конвертером силы, если хотите изучить различные единицы измерения точечных нагрузок и расчета сил.

Калькулятор балок: реакции опор, изгибающий момент, напряжения

Этот онлайн-калькулятор балки рассчитывает силы и моменты , , , в двух подшипниках (= опорные реакции), а также углы наклона статически определенных или
статически неопределимые балки.Кроме того, поперечная сила , изгибающий момент , , напряжение изгиба и
отклонение может быть определено в желаемом месте. Изгибающий момент, поперечная сила и прогиб как функция длины x показаны.
графически в виде двух диаграмм . Расчет максимального изгибающего момента , максимального напряжения изгиба ,
максимальное отклонение и соответствующее положение также возможно.

Подшипники могут быть выполнены в виде неподвижного подшипника, подвижного подшипника, фиксированного зажима или свободного конца. В качестве нагрузки, равной нагрузки или точечной нагрузки, или их комбинации, или треугольной нагрузки.
(влево или вправо) можно выбрать.

* Чтобы ввести эти значения, выберите в разделе «Поперечное сечение A» -> «Другие профили» -> «Собственный профиль».

** Модуль упругости вводится автоматически при выборе материала и может быть изменен в любой момент; подходящих значений вы можете найти, например, в википедии.

Осторожно:

Для профилей с отверстием только I, W и максимальное напряжение изгиба правильно рассчитываются с помощью дополнительных функций. Для других значений выберите профиль без отверстия!

С помощью этого калькулятора можно рассчитать опорные силы как статически определенных, так и статически неопределенных систем. Возможны следующие комбинации:

Страница создана в августе 2019 года. Последнее изменение: 24 октября 2020 года.

Калькулятор для инженеров — изгибающий момент и поперечное усилие для балки с простой опорой

Избранные ссылки

Калькулятор преобразования напряжения
Расчет главного напряжения, максимального напряжения сдвига и их плоскостей

Калькулятор для анализа подвижной нагрузки
Для определения абсолютного макс. Б.М. из-за движущихся грузов.

Калькулятор преобразования напряжения
Расчет главного напряжения, максимального напряжения сдвига и их плоскостей

Калькулятор момента инерции
Расчет момента инерции плоских сечений e.грамм. швеллер, уголок, тройник и др.

Калькулятор железобетона
Расчет прочности железобетонной балки

Калькулятор распределения моментов
Решение неопределенных балок

Калькулятор прогиба и уклона
Расчет прогиба и уклона свободно опертой балки для многих случаев нагружения

Калькулятор фиксированной балки
Инструмент для расчета изгибающего момента и поперечной силы для фиксированной балки для многих случаев нагружения

Калькулятор BM и SF для консоли
Расчет SF и BM для консоли

Калькулятор прогиба и наклона консоли
Для многих случаев нагружения консоли

Вычислитель выступающей балки
Для SF и BM многих случаев нагружения выступающей балки

Дополнительные ссылки

Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства

Научные статьи
Исследования, диссертации и диссертации

Небоскребы мира
Высокие здания мира

Предстоящие конференции
Список конференций, семинаров и практикумов по гражданскому строительству

Профиль инженеров-строителей
Познакомьтесь с выдающимися инженерами-строителями

Профессиональные общества
Всемирные профессиональные общества инженеров-строителей

Продолжайте посещать, чтобы получать обновления или присоединяйтесь к нашему списку рассылки, чтобы получать обновления

Поищите на нашем сайте больше…

Расскажите о нас своим друзьям

Другие полезные ссылки

Калькулятор изгибающего момента и поперечной силы

Bendingmomentdiagram.com — это бесплатный онлайн-калькулятор, который генерирует диаграммы изгибающего момента (BMD) и диаграммы поперечного усилия (SFD) для большинства простых балок. Калькулятор полностью настраивается для работы с большинством балок; эта функция недоступна в большинстве других калькуляторов. Программное обеспечение работает на базе SkyCiv, предлагая мощное программное обеспечение для структурного анализа и проектирования в облаке.

Инструмент полностью функциональный, поэтому посетите наше Бесплатное программное обеспечение Beam, чтобы начать работу! Он будет работать со всеми опорными, определяющими балками и способен воспринимать точечные нагрузки, сосредоточенные моменты и распределенные нагрузки. Кроме того, его можно легко настраивать и настраивать, чтобы вы могли создавать свои собственные лучи. Это чрезвычайно точный инструмент и, в отличие от современных калькуляторов, очень удобный. Это чрезвычайно полезный инструмент для студентов университетов, колледжей и старшеклассников, которым утомительно приходится перерисовывать BMD и SFD для заданий и практических / учебных вопросов.

У нас также есть Учебная страница, которая поможет студентам университетов с расчетами, ожидаемыми в их инженерной степени, а также школьникам. Эти студенты могут научиться рассчитывать и создавать диаграммы поперечной силы и изгибающего момента, и мы понимаем, что процесс анализа балки иногда может быть трудным, поэтому мы предоставили простое пошаговое руководство по расчету диаграмм изгибающего момента и поперечной силы. Включены простые уравнения и формулы изгибающего момента, которые хорошо помогают в ваших расчетах.Существуют также примеры и генераторы случайных балок, которые позволят вам поэкспериментировать с тем, как различные нагрузки влияют на расчет балки, а также на поперечную силу и изгибающий момент балки.

Схема

Bending Moment Diagram разработана командой SkyCiv Engineering, которая предлагает пакеты для студентов и профессионалов, которые предоставляют пользователям доступ к разнообразному программному обеспечению для проектирования конструкций для выполнения работы. Все учетные записи основаны на подписке, поэтому вы можете ежемесячно оплачивать программное обеспечение по мере необходимости! Больше никаких проблем с установкой, загрузкой или лицензированием!

Калькулятор деревянных балок | Какой размер мне нужен?

Рассчитайте размер, необходимый для балки, фермы или заголовка, изготовленных из No.2 сосны или LVL. Охватывает любой пролет и любую нагрузку с высокой точностью. Дважды проверьте себя с помощью этих диаграмм. Работает только с равномерно распределенными нагрузками.

Есть два разных типа нагрузок. Это либо внешняя, либо внутренняя нагрузка. Другими словами, он будет либо на внешней стене, либо где-то внутри. Нагрузка на внешнюю стену с чистыми пролетными фермами составляет ровно половину нагрузки на каждую стену. Например, если размер здания составляет 24 x 24 дюйма, и в нем есть фермы, а нагрузка на крышу будет составлять 30 фунтов снеговой нагрузки, а потолок без хранилища будет таким.Это будет вдвое больше нагрузки на внешние стены по сравнению со зданием с центральной стеной. Калькулятор учитывает все это. Вам нужно только выбрать все применяемые нагрузки.

Большинство внутренних балок должны учитывать нагрузку на крышу. Если есть какие-либо вопросы по другому поводу, вам следует обратиться к поставщику или инженеру. Этот калькулятор соответствует 90% приложений в Международной книге кодов жилищного строительства 2012 года.

Здравый смысл

По моему опыту никогда не использовать балку меньше двухслойной 2 x 8.Независимо от того, что говорят спецификации. Эти небольшие области обычно представляют собой дверные проемы внутри, и людей учат, что эти области являются самым надежным местом в доме в случае возникновения чрезвычайной ситуации.

Подшипник

Согласно кодам IRC 2012 года любая балка, балка или коллектор никогда не должны иметь наклон менее 1 1/2 дюйма. Что-нибудь 5 ‘и выше мы всегда как минимум вдвое калечим. На более длинных пролетах балке может потребоваться гораздо больше места для опоры, как указано в этой таблице.

Крепление

Балки, состоящие из более чем одного слоя, необходимо скреплять вместе гвоздями или болтами.Код IRC 2012 года требует минимум 32 ″ O.C. в шахматном порядке с использованием гвоздя размером не менее 3 ″ на 120 ″. На собственном опыте мы научились использовать гвоздь с пазом размером не менее 3 1/4 дюйма x 131 дюйм в столбике из четырех на каждую ногу вниз по ламинату.

Единственный случай, когда вам когда-либо понадобится использовать болты, будет, если материал будет иметь такие серьезные деформации, как плохая «чашка», которую невозможно преодолеть гвоздями.

Онлайн калькулятор луча

| Калькулятор изгибающего момента и силы сдвига выступающей балки

NEWS | ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ | ЛИСТ

Бесплатный онлайн-калькулятор предназначен для расчета величины поперечной силы и изгибающего момента в точке свисающей балки, несущей равномерно распределенную нагрузку (UDL), или точечной нагрузки в любой точке по длине.

Он даже обеспечивает количество наивысшего изгибающего момента, в котором его местоположение появляется. Калькуляторы соответствуют установленным формулам для поперечной силы и изгибающего момента нависающей балки и предложены преподавателями колледжа.

В случае объединения нагрузок можно применить закон суперпозиции для вычисления результирующих величин.

Примеры нагрузки для выступающей балки: калькулятор предлагает результаты для поперечной силы и изгибающего момента на части выступающей балки, вероятно, по отношению к точечной нагрузке на пролете.Вычисленные величины можно использовать для набросков изгибающего момента и поперечной силы.

Калькулятор также можно использовать для определения ординат диаграммы линий влияния для зданий.

Равномерная нагрузка на балку: калькулятор предлагает результаты для поперечной силы и изгибающего момента на части выступающей балки, вероятно, в отношении равномерно распределенной нагрузки на участке пролета. Пожалуйста, сделайте ссылку на представление и введите количество нагрузки и пролеты в форму, представленную ниже, а затем нажмите «Рассчитать».

Предполагается, что все восходящие рабочие нагрузки положительны, а нисходящие — отрицательны.

Онлайн-калькуляторы изгибающего момента и поперечной силы выступающей балки.

Прочтите следующий видеоурок, чтобы получить дополнительную информацию.

Лектор: Параг Пал

.

Мост Форт Бридж

Вечером 28 декабря 1879 года во время жестокого шторма несколько пролетов стоечно-балочного моста, соединявшего берега залива Ферт-оф-Тей, обрушились в воду, унеся с собой 70 жизней. Репутация его проектировщика была погублена, и его планы по строительству нового моста на этой же железнодорожной линии пошли прахом.

Теперь эту задачу поставили перед инженерами Джоном Фаулером и Бенджамином Бейкером. Им предстояло спроектировать мост через Ферт-оф-Форт и вернуть доверие пассажиров железной дороги. Сделать это можно было лишь при условии, что конструкция не только зарекомендует себя прочной на деле, но и будет выглядеть таковой.

Осмотрев предполагаемые места постройки и изучив русло реки, инженеры приняли решение построить мост в районе деревень Норт-Куинсферри и Саут-Куинсферри, находящихся на расстоянии 2,5 километра друг от друга. Примерно две трети этого пространства занимала водная гладь залива. И снова перед инженерами встал ключевой вопрос: как строить? От идеи стоечно-балочной конструкции отказались довольно быстро: глубина залива местами достигает 67 метров, и это делало возведение опор невозможным. Подвесной железнодорожный мост был недостаточно надежным, да и выглядел бы он легковесно.

В конце концов проектировщики остановились на конструкции, состоящей из трех огромных консольных балок и двух подвесных секций меньшего размера. Центральную консольную балку планировали установить на маленьком островке Инчгарви, южную — настолько близко к центральной, насколько позволит глубина. На таком же расстоянии от центральной балки, как южная, предстояло разместить и северную балку.

Консольная балка — это горизонтальная балка, прикрепленная к опоре только одним концом. В мостостроении две консольные балки монтируются навстречу друг другу и выступают в роли опор для навесной конструкции между ними. Пример с мостом Британия инженера Стефенсона показал, как, увеличивая толщину обычной балки, можно уменьшить ее прогиб. Так как наибольший прогиб приходится на середину балки, именно там толщина ее сечения должна быть максимальной. На мосту через Ферт-оф-Форт для поддержания равновесия и усиления конструкции два рукава консольной балки закреплены на каждой из опор в противоположном друг от друга направлении. Вместе они образуют большую и очень прочную балку. Опоры моста находятся в центре этой балки, поддерживая самую массивную ее часть, на которую направлена основная нагрузка. Чем дальше от опоры, тем меньше нагрузка на балку, прогиб уменьшается, поэтому металлические детали консолей можно сделать тоньше. Три консольные балки моста Форт- бридж соединены между собой при помощи подвесных секций. В результате получается одна сквозная балка на нескольких опорах. Подвесные пролеты крепятся к консолям специальными шарнирами, благодаря чему нагрузка передается на опоры моста.

Два рукава консольных балок или ферм моста в центре крепятся на конструкцию, опирающуюся на четыре массивных опоры. Из этих двенадцати опор шесть строились на такой глубине, что для этого потребовалось использовать пневматические кессоны — специальные устройства для работы под водой. Кессоны представляли собой цилиндры из кованого железа 18 метров в диаметре и около 18 метров в высоту. К месту стройки их привезли в разобранном виде, собрали на берегу, а затем отбуксировали к месту назначения и затопили. Рабочая камера на дне кессона соединялась с верхней платформой тремя шахтами: две из них использовались для транспортировки строительных материалов, а третья — для перевозки рабочих. Доступ в каждую из шахт осуществлялся через воздушный шлюз. Воду из рабочей камеры вытесняли, закачивая в нее сжатый воздух.

Таким образом, люди могли достаточно безопасно трудиться на дне залива. По мере того как они вынимали со дна рыхлую илистую породу и отправляли ее наверх, пространство поверх кессона заполняли бетоном. Вес кессона постепенно увеличивался, и он медленно погружался все глубже в морской грунт. Как только кессон достигал твердой породы, строители поднимались наверх, а рабочую камеру заполняли бетоном. После того как были построены все опоры, на них установили массивные стальные конструкции. Пять труб, сходящиеся на каждой несущей опоре, приклепаны к ней и друг к другу. Как и в случае с виадуком Гараби, для большей устойчивости детали моста внизу более мощные.

Таким образом, нагрузка от ветра, а также от проходящих поездов передается через консольные фермы трем огромным, сложным по конструкции металлическим башням моста, основные трубы которых имеют 3,5 метра в диаметре. Установка опор и монтаж башен заняли больше половины времени, потребовавшегося для возведения всего моста. Луцию Фабрицию, руководившему строительством моста Фабричо, такой размах пришелся бы по вкусу!

Фаулер и Бейкер спроектировали воистину грандиозное сооружение, перед которым бессильна природная стихия. Масштаб конструкции настолько велик, что проезжающий по мосту поезд кажется игрушечным. Ее мощь и основательность действовали успокаивающе даже на самых скептически настроенных пассажиров. Однако творение двух инженеров оказалось очень дорогостоящим, и его крайне редко пытались копировать. Единственный консольный мост, превосходящий по длине Форт бридж, — это построенный в 1919 году Квебекский мост.

Дэвид Маколи. Как это построено: от мостов до небоскребов.
Иллюстрированная энциклопедия

Прокатная балка онлайн

Момент сопротивления слишком большой, возможны большие перенапряжения! Перенапряжение должны быть не более 5%! Скорее всего нужного профиля в сортаменте (ГОСТ 8239-72) нет, попробуйте найти ГОСТ 26020-83.

Значение опорных реакций (положительная — направлена вниз, отрицательная — вверх):

R_A= кН

R_B= кН

Значение усилий в произвольном сечении:

Координата x= 2345678910СправаСлева

Значение эпюры Q при x= м: кН

Значение эпюры M при x= м: кН·м

Значение эпюры при x= м: кН·м²·рад

Значение эпюры при x= м: кН·м³

Начальные параметры:

кН

кН·м

кН·м²·рад

кН·м³

Максимальные значения усилий:

Подбор поперечного сечения.

Нужный момент сопротивления:

_тр см ³

Из таблицы сортамента (ГОСТ 8239-72) принимаем двутавр №, с такими геометрическими характеристиками:

см⁴;    см³;    см³.

Размеры сечения:

мм;    мм;    мм;    мм.

Полная проверка прочности балки.

а) По максимальным нормальным напряжением (сечение при м).

МПа

% — недонапряжение. перенапряжение.

б) По максимальным касательным напряжением (сечение при м).

МПа

% — недонапряжение. перенапряжение.

Вычисляем статический момент полки двутавра относительно центральной оси :

см³,

касательное напряжение в точке стыка полки и стенки:

МПа.

в) Главные напряжения проверяем в (сечение при м, СправаСлева).

Усилия в сечении: кН·м,   кН.

Определяем нормальное и касательное напряжение в точке стыка полки и стенки двутавра:

МПа;

МПа.

По четвертой теории прочности:

МПа

% — недонапряжение. перенапряжение.

Определяем касательное напряжение на нейтральной оси:

МПа.

Эпюра поперечных сил:

Определить максимум на эп. Q

Эпюра изгибающих моментов:

Определить максимум на эп. M

Эпюра углов поворота:

Определить максимум на эп. EIφ

Эпюра прогибов:

Определить максимум на эп. EIw

Прогиб балки

, Расс Эллиот Благодарности : Существует ряд стандартных работ, касающихся принципов отклонения балки. Особенно хорошее изложение, на котором основаны приведенные здесь уравнения, содержится в Механика материалов (четвертое издание SI) Дж.М. Гира и С.П. Тимошенко, Стэнли Торнса, ISBN 0 7487 3998 X. Следует сделать ссылку на эта работа для вывода уравнений. Введение Прогиб пружинной балки зависит от ее длины, формы поперечного сечения, материала, места приложения отклоняющей силы и того, как балка поддерживается. Уравнения, приведенные здесь, относятся к однородным, линейно упругим материалам, в которых вращение балки невелико. В следующих примерах рассматриваются только нагрузки, действующие в одной точке или отдельных точках — точка приложения силы F на диаграммах предназначена для обозначения рожкового блока модели локомотива (или буксы транспортного средства), способного перемещаться вертикально. в рупорной направляющей и действуя против силы пружинной балки, прикрепленной к локомотиву или основным шасси транспортного средства или переносимых ими.Доля общего веса, действующего на каждую ось локомотива или транспортного средства, будет зависеть от положения его центра тяжести по отношению к оси (или точек крепления уравновешивающих балок шасси, если они используются). Приложение к модели локомотивных рожковых блоков Как видно из уравнений, толщина материала ( h или d ) очень важна, и, следовательно, увеличивающиеся размеры в диапазоне доступных гитарных струн делают их очень привлекательными для использования в качестве пружинные балки.Также существует значительная разница в прогибе балки для данной силы, в зависимости от того, как она поддерживается и фиксируется, а также от того, поддерживается ли она только на одном конце или на обоих концах. Предполагается, что конструкция должна быть основана на заданном прогибе рогового блока, а затем определить, какая длина, толщина и стиль балки наиболее подходят для конкретной силы, которая должна поддерживаться каждой осью. Для локомотивов, вес которых составляет от 4 до 6 граммов на тонну прототипа, массы, поддерживаемые каждым отдельным роговым блоком локомотива, вероятно, будут находиться в диапазоне от 30 до 60 граммов (что соответствует загрузке прототипа от 14 до 20 тонн на тонну). ось). Выбор значения отклонения Для разумной гусеницы с мелким масштабом 4 мм рекомендуемое значение прогиба рогового блока, δ , при конечной нагрузке локомотива составляет 0,5 мм. Приведенная выше рекомендация, как известно, является чрезмерно упрощенным и, возможно, неверным предположением о том, каким должно быть расчетное значение прогиба, и вызвала серьезные споры. Приветствуется любой опыт применения этой рекомендации в реальной практике моделирования шасси — цель этой статьи — начало обсуждения, а не его заключение.Щелкните здесь для первоначального изучения вопросов по этому вопросу. Момент инерции, I Момент инерции прямоугольного сечения I = bh 3 ∕ 12 где h — размер в плоскости изгиба, т. Е. По оси, по которой действует изгибающий момент Момент инерции круглого сечения I = π r 4 ∕ 4 = π d 4 ∕ 64 , где r и d — радиус и диаметр соответственно Все приведенные ниже уравнения содержат I , момент инерции балки, который является константой, определяемой формой и толщиной поперечного сечения балки.Момент инерции не зависит от длины или материала балки. Здесь рассматриваются только прямоугольные и круглые цельные сечения. Пояснения к схемам прогиба и обозначениям На схемах показаны два типа опор: фиксированная и простая. На неподвижной опоре балка удерживается жестко, а угловой прогиб в точке крепления равен нулю. На простой опоре балка может скользить по опоре и вращаться в соответствии с силой, приложенной к балке. L = длина балки a = промежуточная длина балки δ = прогиб балки F = сила (т. Е. Доля веса локомотива, которому оказывает сопротивление букса) E = модуль Юнга I = момент инерции балки Уравнения и диаграммы прогиба Примечание к схемам и уравнениям .Приведенные здесь диаграммы были перевернуты по сравнению с их обычным представлением в учебниках, чтобы отразить их применение для моделей локомотивов и букс транспортных средств. Тем не менее, хотя уравнения для отклонения были согласованы с их описанием в учебниках, нормальное соглашение о знаках (+ или — для обозначения отклонений по вертикальной оси y от опорной линии балки) было проигнорировано, поскольку мы здесь обеспокоены. только с абсолютной величиной прогиба балки. Концевая нагрузка на консольную балку с одиночной фиксированной опорой δ = FL 3 ∕ 3 EI Это уравнение также следует использовать для отклонения уравнительной балки, вращающейся вокруг фиксированной оси и опирающейся на два рупорных блока по обе стороны от оси поворота. Двойные нагрузки на балку с двумя простыми опорами (примеры применения этой конфигурации) Это может быть применено для двух роговых блоков, прижимающихся к одной балке. Прогиб на расстоянии a от соседней опоры составляет: δ = Fa 2 (3 L -4 a ) ∕ 6 EI Свисающая нагрузка на балку, ограниченная двумя простыми опорами δ = Fa 2 ( L + a ) ∕ 3 EI Промежуточная / центральная нагрузка на балку с одной фиксированной и одной простой опорой Прогиб на длине a от неподвижной опоры составляет: δ = Fa 3 ( L — a ) 2 (4 L — a ) ∕ 12 EIL 3 Для нагрузки в центре балки, подставив в приведенное выше уравнение a = L the 2 , прогиб составит: δ = 3.5 FL 3 ∕ 384 EI Центральная нагрузка на балку с двумя неподвижными опорами δ = FL 3 ∕ 192 EI При нагрузке в центре отклонение на расстоянии a от фиксированной опоры (где a меньше чем или равно L ∕ 2 ) составляет: δ = Fa 2 (3 L -4 a ) ∕ 48 EI Промежуточная нагрузка на балку с двумя неподвижными опорами Прогиб на расстоянии a от неподвижной опоры составляет: δ = 2 Fa 3 ( L — a ) 2 ∕ 3 EI (2 а + L ) 2 Значения модуля Юнга, E Бериллий медный 124 ГПа 1 Латунь, твердость 70/30 117.2 ГПа Латунь неуточненная от 96 до 110 ГПа Нейзильбер 132,5 ГПа (127 ГПа 1 ) Бронза фосфористая, 5%, твердая 131,8 ГПа Фосфорно-бронзовая (92% Cu / 8% Sn или CuSn8) 111 ГПа 1 Сталь, малоуглеродистая или инструментальная 212 ГПа Сталь мягкая, низкоуглеродистая 210 ГПа Сталь мягкая (закаленная) 201.4 ГПа Сталь нержавеющая 215,2 ГПа (190 ГПа 1 ) Сталь инструментальная (закаленная) 203,2 ГПа Следует отметить, что это теоретические значения. Типичное значение для стальной гитарной струны можно принять как 205 ГПа. Значения, указанные для фосфористой бронзы, различаются: кажется, что они будут зависеть от того, является ли материал «пружинным» или «экстрапружинным» типом фосфористой бронзы 92% Cu / 8% Sn. обычно используется в переключателях с защелкой. 1 Шигли, Отдел машиностроения, 1980, McGraw Hill Примечания к агрегатам и размерам 1 Па = 1 Н · м -2 = 10 -6 Н · мм -2 = 10 -6 кг · м · с -2 · мм -2 = 1 г · мм -1 · с -2 Для получения силы F в приведенных выше уравнениях следует умножить массу на гравитационную постоянную г (9.81 м · с -2 , или, что нам удобнее, 9810 мм · с -2 ) Размеры модуля Юнга E составляют ML -1 T -2 Размеры усилия F составляют L 2 ML -1 T -2 = MLT -2 Размеры момента инерции I составляют L 4 © Расс Эллиотт , впервые опубликовано 19 апреля 2000 г .; небольшая редакционная правка, август 2001 г .; уравнение для промежуточной нагрузки на балку с двумя фиксированными опорами исправлено, и уравнение прогиба для промежуточной / центральной нагрузки на балку с одной фиксированной и одной простой опорой повторно выражено, январь 2005 г .; Диаграмма для свисающей нагрузки на балку, ограниченную двумя простыми опорами, пересмотрена 8 октября 2009 г .; Уравнение промежуточной нагрузки на балку с двумя неподвижными опорами исправлено, 30 декабря 2010 г.

% PDF-1.3 % 790 0 объект> эндобдж xref 790 87 0000000016 00000 н. 0000003638 00000 н. 0000002077 00000 н. 0000003742 00000 н. 0000003768 00000 н. 0000003814 00000 н. 0000004206 00000 н. 0000004286 00000 п. 0000004366 00000 н. 0000004446 00000 н. 0000004526 00000 н. 0000004606 00000 н. 0000004686 00000 н. 0000004766 00000 н. 0000004846 00000 н. 0000004926 00000 н. 0000005006 00000 н. 0000005086 00000 н. 0000005166 00000 н. 0000005246 00000 н. 0000005326 00000 н. 0000005405 00000 н. 0000005484 00000 н. 0000005563 00000 н. 0000005642 00000 п. 0000005721 00000 н. 0000005800 00000 н. 0000005879 00000 п. 0000005958 00000 н. 0000006037 00000 н. 0000006116 00000 п. 0000006195 00000 н. 0000006274 00000 н. 0000006353 00000 п. 0000006432 00000 н. 0000006511 00000 н. 0000006590 00000 н. 0000006669 00000 н. 0000006748 00000 н. 0000006827 00000 н. 0000006906 00000 н. 0000006985 00000 п. 0000007064 00000 н. 0000007143 00000 н. 0000007222 00000 н. 0000007301 00000 п. 0000007380 00000 н. 0000007459 00000 н. 0000007538 00000 н. 0000007616 00000 н. 0000007694 00000 п. 0000007772 00000 н. 0000008144 00000 н. 0000012271 00000 п. 0000012850 00000 п. 0000013048 00000 н. 0000013549 00000 п. 0000019289 00000 п. 0000019998 00000 п. 0000020324 00000 п. 0000020906 00000 п. 0000027647 00000 н. 0000028472 00000 п. 0000028889 00000 п. 0000028957 00000 п. 0000029405 00000 п. 0000030554 00000 п. 0000030916 00000 п. 0000031438 00000 п. 0000032252 00000 п. 0000032281 00000 п. 0000032366 00000 п. 0000032798 00000 п. 0000033385 00000 п. 0000034526 00000 п. 0000034622 00000 п. 0000034714 00000 п. 0000035389 00000 п. 0000036044 00000 п. 0000036678 00000 п. 0000036774 00000 п. 0000037386 00000 п. 0000038153 00000 п. 0000038785 00000 п. 0000039357 00000 п. 0000039385 00000 п. 0000003444 00000 н. трейлер ] >> startxref 0 %% EOF 792 0 obj> поток xb«b`tg`

Фототермическая спектроскопия отклонения кантилевера | EPJ Techniques and Instrumentation

1.

Thundat T, Warmack RJ, Chen GY, Allison DP: Отклонения консолей сканирующего силового микроскопа, вызванные температурой и окружающей средой. Appl Phys Lett 1994, 64: 2894–2896. 10.1063 / 1.111407

ADS Статья Google Scholar

2.

Gimzewski JK, Gerber C, Meyer E, Schlittler RR: Наблюдение химической реакции с помощью микромеханического датчика. Chem Phys Lett 1994, 217: 589–594.10.1016 / 0009-2614 (93) E1419-H

ADS Статья Google Scholar

3.

Baller MK, Lang HP, Fritz J, Gerber C, Gimzewski JK, Drechsler U, Rothuizen H, Despont M, Vettiger P, Battiston FM, Ramseyer JP, Fornaro P, Meyer E, Güntherodt HJ: искусственный нос на основе кантилевера. Ультрамикроскопия 2000, 82: 1–9. 10.1016 / S0304-3991 (99) 00123-0

Артикул Google Scholar

4.

Фриц Дж., Баллер М.К., Ланг Х.П., Ротуйзен Х., Веттигер П., Мейер Э., Гюнтеродт Х.Дж., Гербер С., Гимжевски Дж. Наука 2000, 288: 316–318. 10.1126 / science.288.5464.316

ADS Статья Google Scholar

5.

Chen GY, Thundat T, Wachter EA, Warmack RJ: Адсорбционное поверхностное напряжение и его влияние на резонансную частоту микрокантилеверов. J Appl Phys 1995, 77: 3618–3622. 10.1063 / 1.359562

ADS Статья Google Scholar

6.

Thundat T, Chen GY, Warmack RJ, Allison DP, Wachter EA: Обнаружение паров с помощью резонирующих микрокантилеверов. Anal Chem 1995, 67: 519–521. 10.1021 / ac00099a006

Артикул Google Scholar

7.

Cherian S, Thundat T: Определение вызванного адсорбцией изменения жесткости пружины микрокантилевера. Appl Phys Lett 2002, 80: 2219–2221. 10.1063 / 1.1463720

ADS Статья Google Scholar

8.

Wachter EA, Thundat T: Микромеханические датчики для химических и физических измерений. Rev Sci Instrum 1995, 66: 3662–3667. 10.1063 / 1.1145484

ADS Статья Google Scholar

9.

Hsieh MD, Zellers ET: Пределы распознавания для простых смесей паров, определенные с помощью набора микросенсоров. Anal Chem 2004, 76: 1885–1895. 10.1021 / ac035294w

Артикул Google Scholar

10.

Then D, Vidic A, Ziegler C: Высокочувствительная автоколебательная консольная решетка для количественного и качественного анализа смесей органических паров. Приводы Sens B 2006, 117: 1–9. 10.1016 / j.snb.2005.07.069

Статья Google Scholar

11.

Zhao W, Pinnaduwage LA, Leis JW, Gehl AC, Allman SL, Shepp A, Mahmud KK: Идентификация и количественная оценка компонентов в тройных паровых смесях с использованием электронного носа на основе микроэлектромеханической системы. J Appl Phys 2008, 103: 104902. 10.1063 / 1.2921866

ADS Статья Google Scholar

12.

Jin C, Kurzawski P, Hierlemann A, Zellers ET: Оценка многопозиционных датчиков для определения смесей органических паров. Anal Chem 2008, 80: 227–236. 10.1021 / ac0715120

Артикул Google Scholar

13.

Jin C, Zellers ET: Пределы распознавания для бинарных и тройных паровых смесей, определенные с помощью массивов с несколькими датчиками. Anal Chem 2008, 80: 7283-7293.10.1021 / ac8008912

Артикул Google Scholar

14.

Barnes JR, Stephenson RJ, Welland ME, Gerber C, Gimzewski JK: Фототермическая спектроскопия с фемтоджоульной чувствительностью с использованием микромеханического устройства. Природа 1994, 372: 79–81. 10.1038 / 372079a0

ADS Статья Google Scholar

15.

Wachter EA, Thundat T, Oden PI, Warmack RJ, Datskos PG, Sharp SL: Дистанционное оптическое обнаружение с помощью микрокантилеверов. Rev Sci Instrum 1996, 67: 3434–3439. 10.1063 / 1.1147149

ADS Статья Google Scholar

16.

Li G, Burggraf LW, Baker WP: Фототермическая спектроскопия с использованием многослойного кантилевера для химического обнаружения. Appl Phys Lett 2000, 76: 1122–1124. 10.1063 / 1.125988

ADS Статья Google Scholar

17.

Дацкос П.Г., Раджич С., Сепаниак М.Дж., Лаврик Н., Типпл С.А., Сенесак Л.Р., Дацкоу I: Химическое обнаружение на основе индуцированных адсорбцией и фотоиндуцированных напряжений в устройствах микроэлектромеханических систем. J Vac Sci Technol B 2001, 19: 1173–1179. 10.1116 / 1.1387082

Артикул Google Scholar

18.

Аракава Е.Т., Лаврик Н.В., Раджич С., Дацкос PG: Обнаружение и дифференциация биологических видов с использованием микрокалориметрической спектроскопии. Ультрамикроскопия 2003, 97: 459–465. 10.1016 / S0304-3991 (03) 00074-3

Артикул Google Scholar

19.

Wig A, Arakawa ET, Passian A, Ferrell TL, Thundat T: Фототермическая спектроскопия Bacillus anthracis и Bacillus cereus с микрокантилеверами. Приводы Sens B 2006, 114: 206–211. 10.1016 / j.snb.2005.04.029

Статья Google Scholar

20.

Krause AR, Van Neste C, Senesac L, Thundat T, Finot E: Обнаружение следов взрывчатых веществ с использованием спектроскопии фототермического отклонения. J Appl Phys 2008, 103: 094906. 10.1063 / 1.21

ADS Статья Google Scholar

21.

Ким С., Ли Д., Лю Х, Ван Несте С., Чон С., Тундат Т: Молекулярное распознавание с использованием безрецепторной наномеханической инфракрасной спектроскопии на основе квантового каскадного лазера. Sci Rep 2013, 3: 1111.

ADS Google Scholar

22.

Багери М., Чае И., Ли Д., Ким С., Тундат Т: Селективное обнаружение физадсорбированных углеводородов с использованием фототермической спектроскопии отклонения кантилевера. Приводы Sens B 2014, 191: 765–769. 10.1016 / j.snb.2013.10.078

Статья Google Scholar

23.

Lee D, Kim S, Van Neste CW, Lee M, Jeon S, Thundat T: Фотоакустическая спектроскопия поверхностно адсорбированных молекул с использованием наноструктурированной матрицы связанных резонаторов. Нанотехнологии 2014, 25: 035501. 10.1088 / 0957-4484 / 25/3/035501

ADS Статья Google Scholar

24.

Хан MF, Kim S, Lee D, Schmid S, Boisen A, Thundat T: Наномеханическая идентификация жидких реагентов в микрофлюидном канале. Лабораторный чип 2014, 14: 1302–1307. 10.1039 / c3lc51273h

Артикул Google Scholar

25.

Ли Д., Ким С., Чхэ И., Чон С., Тандат Т: Микрокантилеверы из TiO2 с рисунком Наноуэлла для калориметрического химического зондирования. Appl Phys Lett 2014, 104: 141903. 10.1063 / 1.4870535

ADS Статья Google Scholar

26.

Пристера Ф, Халик М, Кастелли А., Фредерикс У: Анализ взрывчатых веществ с помощью инфракрасной спектроскопии. Anal Chem 1960, 32: 495–508. 10.1021 / ac60160a013

Артикул Google Scholar

27.

Lewis IR, Daniel NW Jr, Griffiths PR: Интерпретация рамановских спектров нитросодержащих взрывчатых материалов. часть i: частота групп и членство в структурных классах. Appl Spectrosc 1997, 51: 1854–1867.10.1366 / 0003702971939686

ADS Статья Google Scholar

28.

Макашир П.С., Куриан Э.М.: Спектроскопические и термические исследования 2,4,6-тринитротолуола (ТНТ). J Therm Anal Cal 1999, 55: 173–185. 10.1023 / A: 1010152626354

Артикул Google Scholar

29.

Макашир П.С., Куриан Э.М.: Спектроскопические и термические исследования тетранитрата пентаэритрита (ТЭН). Propell Explos Pyrot 1999, 24: 260–265. 10.1002 / (SICI) 1521-4087 (199908) 24: 4 <260 :: AID-PREP260> 3.0.CO; 2-I

Артикул Google Scholar

30.

Beal RW, Brill TB: Колебательное поведение группы –NO2 в энергетических соединениях. Appl Spectrosc 2005, 59: 1194–1202. 10.1366 / 000370205774430873

ADS Статья Google Scholar

31.

Yoon S, Son J, Lee W, Lee H, Lee CW: Прогноз содержания битума в нефтеносном песке на основе измерения FT-IR. J Ind Eng Chem 2009, 15: 370–374. 10.1016 / j.jiec.2008.11.005

Статья Google Scholar

32.

Довбешко Г.И., Гридина Н.Ю., Круглова Е.Б., Пащук О.П.: FTIR-спектроскопические исследования повреждений нуклеиновых кислот. Таланта 2000, 53: 233–246. 10.1016 / S0039-9140 (00) 00462-8

Артикул Google Scholar

33.

Ким С., Ли Д., Тундат Р., Багери М., Чон С., Тандат Т: Фототермическая спектроскопия отклонения кантилевера. ECS Trans 2013, 50: 459–464. 10.1149 / 05012.0459ecst

Артикул Google Scholar

34.

Матео-Марти Э., Брионес С., Роман Э., Бриан Э, Прадье С.М., Мартин-Гаго JA: Самособирающиеся монослои пептидных нуклеиновых кислот на золотых поверхностях: спектроскопическое исследование. Langmuir 2005, 21: 9510–9517. 10.1021 / la050366v

Артикул Google Scholar

35.

Liao W., Wei F, Liu D, Qian MX, Yuana G, Zhaoa XS: FTIR-ATR обнаружение белков и малых молекул посредством конъюгации ДНК. Приводы Sens B 2006, 114: 445–450. 10.1016 / j.snb.2005.06.021

Статья Google Scholar

36.

Lai J, Perazzo T, Shi Z, Majumdar A: Оптимизация и повышение производительности микромеханических термодатчиков высокого разрешения. Приводы Sens A 1997, 58: 113–119. 10.1016 / S0924-4247 (96) 01401-X

Артикул Google Scholar

Измерение изгиба балки кантилевера методом оптического рычага и его приложение к поверхностным напряжениям

Консольные балки, как микроскопические, так и макроскопические, используются в качестве датчиков в самых разных областях применения.Система оптических рычагов обычно используется для определения отклонения и, следовательно, профиля кантилевера под нагрузкой. Чувствительность оптического рычага должна быть откалибрована, и это обычно достигается приложением известной нагрузки или отклонения к свободному концу кантилевера. Когда операция измерения включает в себя другой тип нагрузки или комбинацию типов нагрузок, калибровка и полученные на ее основе значения прогиба становятся недействительными. Здесь мы разрабатываем основное уравнение, которое позволяет получить истинное отклонение кантилевера просто путем измерения кажущегося прогиба для равномерно распределенных нагрузок и нагрузок конечным моментом.Эти нагрузки имеют отношение к равномерной адсорбции или наложению материала на кантилевер или к приложению поверхностного напряжения к кантилеверу и должны помочь экспериментаторам, использующим оптический рычаг, например, в атомно-силовом микроскопе, для измерения отклонений кантилевера в большом количестве. зондирования приложений. Затем мы применяем эту обработку для экспериментальной оценки поверхностного напряжения. Получены три формы уравнения Стони, которые связывают кажущееся отклонение с поверхностным напряжением, которое справедливо как для макроскопических, так и для микроскопических экспериментов.Также представлен анализ ошибок, возникающих из-за неправильного моделирования условий нагружения кантилевера, применяемого в настоящее время в экспериментах. Показано, что опубликованные в литературе значения поверхностного напряжения в микроскопических экспериментах обычно на 9% меньше их истинного значения. Для макроскопических экспериментов мы демонстрируем, что добавленная масса пленки или покрытия обычно преобладает над измеряемым прогибом и должна быть учтена точно, если необходимо провести измерения поверхностного напряжения.Кроме того, в сообщаемых измерениях обычно используется форма уравнения Стони, которая ошибочна, что приводит к завышению оценки поверхностного напряжения более чем в 5 раз.

Пьезорезистивные кантилеверы для АСМ, превосходящие стандартное отклонение оптического луча при формировании топографических изображений с низким уровнем шума.

Бинниг, Г., Куат, К. Ф. и Гербер, К. Атомно-силовой микроскоп. Phys. Rev. Lett. 56, 930–933 (1986).

ADS CAS Статья Google Scholar

Мейер, Г.& Амер, Н. М. Новый оптический подход к атомно-силовой микроскопии. Прил. Phys. Lett. 53, 1045–1047 (1988).

ADS Статья Google Scholar

Alexander, S. et al. Атомно-силовой микроскоп с атомным разрешением, реализованный с помощью оптического рычага. J. Appl. Phys. 65, 164–167 (1989).

ADS CAS Статья Google Scholar

Фукума, Т., Кимура, М., Kobayashi, K., Matsushige, K. & Yamada, H. Разработка малошумящего датчика отклонения кантилевера для атомно-силовой микроскопии с частотной модуляцией в различных средах. Rev. Sci. Instrum. 76, 053704 (2005).

ADS Статья Google Scholar

Эннинг Р. Высокочастотная атомно-силовая микроскопия. Кандидатская диссертация, Высшая техническая школа Цюрихского университета, Швейцария, факультет машиностроения и технологического проектирования (2011 г.).

Итон, П.И Вест П. Атомно-силовая микроскопия. Гл. 6.6.3, 135–137 (Oxford University Press, 2010).

Li, M., Tang, H. X. & Roukes, M. L. Сверхчувствительные кантилеверы на основе NEMS для измерения, сканирования зонда и приложений с очень высокой частотой. Nat. Nanotechnol. 2. С. 114–120 (2007).

ADS CAS Статья Google Scholar

Кодера, Н., Ямамото, Д., Исикава, Р. и Андо, Т. Видеоизображение шагающего миозина V с помощью высокоскоростной атомно-силовой микроскопии.Nature 468. С. 72–76 (2010).

ADS CAS Статья Google Scholar

Brugger, J., Buser, R.A. & Rooij, N. F. de. Микро-зонд атомной силы со встроенным емкостным считывающим устройством. J. Micromechanics Microengineering 2, 218–220 (1992).

ADS CAS Статья Google Scholar

Blanc, N. Сканирующая силовая микроскопия в динамическом режиме с использованием емкостных сенсоров микроизготовления.J. Vac. Sci. Technol. В 14, 901–905 (1996).

CAS Статья Google Scholar

Forsen, E. et al. Сверхчувствительный датчик массы, полностью интегрированный с дополнительной схемой металл-оксид-полупроводник. Прил. Phys. Lett. 87, 043507 (2005).

ADS Статья Google Scholar

Ким, С. Дж., Оно, Т. и Эсаши, М. Емкостной резонансный датчик массы с обнаружением частотной демодуляции на основе резонансного контура.Прил. Phys. Lett. 88, 053116 (2006).

ADS Статья Google Scholar

Verd, J. et al. Монолитный датчик массы, изготовленный по традиционной технологии с разрешением аттограммы в условиях воздуха. Прил. Phys. Lett. 91, 013501 (2007).

ADS Статья Google Scholar

Tortonese, M., Barrett, R.C. и Quate, C.F. Атомное разрешение с помощью атомно-силового микроскопа с использованием пьезорезистивного детектирования.Прил. Phys. Lett. 62, 834–836 (1993).

ADS CAS Статья Google Scholar

Линнеманн Р., Готсалк Т., Хаджийски Л. и Рэнджлоу И. В. Характеристика кантилевера со встроенным датчиком отклонения. Тонкие твердые пленки 264, 159–164 (1995).

ADS CAS Статья Google Scholar

Jumpertz, R., Hart, A. v. D., Ohlsson, O., Зауренбах Ф. и Шелтен Дж. Пьезорезистивные датчики на кантилеверах АСМ с атомным разрешением. Микроэлектрон. Англ. 41–42, 441–444 (1998).

Артикул Google Scholar

Thaysen, J., Boisen, A., Hansen, O. & Bouwstra, S. Зонд для атомно-силовой микроскопии с пьезорезистивным считыванием и высокосимметричным мостом Уитстона. Датчики Актуаторы, Физ. 83, 47–53 (2000).

CAS Статья Google Scholar

Ю., Х., Тайсен, Дж., Хансен, О. и Бойзен, А. Оптимизация чувствительности и шума в пьезорезистивных кантилеверах. J. Appl. Phys. 92, 6296–6301 (2002).

ADS CAS Статья Google Scholar

Yoshikawa, G. et al. Обнаружение паров на уровне ниже ppm с помощью пьезорезистивных датчиков с матрицей микрокантилеверов. Нанотехнологии 20, 015501 (2009).

ADS Статья Google Scholar

Кукла, Дж.C. & Pruitt, B.L. Широкополосные пьезорезистивные датчики силы со встроенным тепловым срабатыванием. J. Micromechanics Microengineering 22, 095012 (2012).

ADS Статья Google Scholar

Тосолини, Дж., Скарпони, Ф., Каннистраро, С. и Баузеллс, Дж. Распознавание биомолекул с использованием пьезорезистивных наномеханических датчиков силы. Прил. Phys. Lett. 102, 253701 (2013).

ADS Статья Google Scholar

Bausells, J.Пьезорезистивные кантилеверы для наномеханического зондирования. Микроэлектрон. Англ. 145, 9–20 (2015).

CAS Статья Google Scholar

Ито Т. и Шуга Т. Разработка датчика силы для атомно-силовой микроскопии с использованием тонких пьезоэлектрических пленок. Нанотехнологии 4, 218–224 (1993).

ADS CAS Статья Google Scholar

Ли, Дж. Х. и др. Иммуноанализ простатоспецифического антигена (ПСА) с использованием сдвига резонансной частоты пьезоэлектрического наномеханического микрокантилевера.Биосенс. Биоэлектрон. 20, 2157–2162 (2005).

ADS CAS Статья Google Scholar

Карабалин Р.Б. и др. Пьезоэлектрические наноэлектромеханические резонаторы на основе тонких пленок нитрида алюминия. Прил. Phys. Lett. 95, 103111 (2009).

ADS Статья Google Scholar

Ivaldi, P. et al. Пьезоэлектрические кантилеверы на основе пленки AlN толщиной 50 нм для гравиметрического обнаружения.J. Micromechanics Microengineering 21, 085023 (2011).

ADS Статья Google Scholar

Клеланд, а. Н. и Роукс, М. Л. Изготовление высокочастотных механических резонаторов нанометрового масштаба из объемных кристаллов Si. Прил. Phys. Lett. 69, 2653–2655 (1996).

ADS CAS Статья Google Scholar

Экинчи, К. Л., Хуанг, X. М. Х. и Роукс, М.L. Сверхчувствительное наноэлектромеханическое обнаружение масс. Прил. Phys. Lett. 84, 4469–4471 (2004).

ADS CAS Статья Google Scholar

Johansson, A., Blagoi, G. & Boisen, A. Полимерные консольные биосенсоры со встроенным считывающим устройством. Прил. Phys. Lett. 89, 173505 (2006).

ADS Статья Google Scholar

Шнайдер А., Ибботсон Р.Х., Данн, Р. Дж. И Хук, Э. Массивы микрокантилеверов SU-8 со встроенными пьезорезистивными датчиками для параллельных приложений АСМ. Микроэлектрон. Англ. 88, 2390–2393 (2011).

CAS Статья Google Scholar

Арлетт, Дж. Л., Мэлони, Дж. Р., Гудлевски, Б., Мулунех, М. и Роукс, М. Л. Самочувствительные микро- и нанокантилеверы с разрешением по силе в масштабе Аттоньютона. Nano Lett. 6. С. 1000–1006 (2006).

ADS CAS Статья Google Scholar

Сяо-мэй, Ю., Xing-liu, J., Thaysen, J., Hansen, O. & Boisen, A. Шум и чувствительность в пьезорезистивных кантилеверах из поликремния. Китайская физ. 10, 918–923 (2001).

ADS Статья Google Scholar

Вильянуэва, Г., Боселлс, Дж., Монтсеррат, Дж. И Перес-Мурано, Ф. Пьезорезистивные кантилеверы из поликремния для определения межмолекулярных сил. в 2005 Испанской конф. Электронные устройства, Proc. 2005, 495–498 (2005).

Артикул Google Scholar

Катрагадда, Р., Wang, Z., Khalid, W., Li, Y. & Xu, Y. Консоли из парилена, интегрированные с пьезорезисторами из поликристаллического кремния для измерения поверхностных напряжений. Прил. Phys. Lett. 91, 083505 (2007).

ADS Статья Google Scholar

Кале, Н. С., Наг, С., Пинто, Р. и Рао, В. Р. Изготовление и характеристика полимерного микрокантилевера с инкапсулированным поликремниевым пьезорезистором CVD с горячим проводом. J. Microelectromechanical Syst.18, 79–87 (2009).

CAS Статья Google Scholar

Шехават, Г., Тарк, С.-Х. И Дравид, В. П. Микрокантилеверы со встроенными МОП-транзисторами для измерения отклонения в биомолекулярных датчиках. Science 311, 1592–1595 (2006).

ADS CAS Статья Google Scholar

Бреннинг, Х. Т. А. и др. Одноэлектронный транзистор на зонде атомно-силового микроскопа.Nano Lett. 6, 937–941 (2006).

ADS CAS Статья Google Scholar

Коппинен П. Дж., Ливонен Дж. Т., Альског М. и Маасилта И. Дж. Измерение деформации с помощью субмикронных туннельных переходов Al-AlO (x) -Al. Rev. Sci. Instrum. 81, 023901 (2010).

ADS CAS Статья Google Scholar

Тосолини, Г., Вильянуэва, Г., Перес-Мурано, Ф. и Боселлс, Дж.Кремниевые микрокантилеверы с обнаружением MOSFET. Микроэлектрон. Англ. 2010. Т. 87. С. 1245–1247.

CAS Статья Google Scholar

Huth, M. et al. Осаждение, индуцированное сфокусированным электронным пучком: перспектива. Beilstein J. Nanotechnol. 3, 597–619 (2012).

CAS Статья Google Scholar

Хансен О. и Бойзен А. Шум в пьезорезистивной атомно-силовой микроскопии.Нанотехнологии 10, 51–60 (1999).

ADS Статья Google Scholar

Парк С.-Дж., Долл Дж. К. и Прюитт Б. Л. Характеристики пьезорезистивного кантилевера — Часть I: Аналитическая модель чувствительности. J. Microelectromech. Syst. 2010. Т. 19. С. 137–148.

Артикул Google Scholar

Долл, Дж. К. и Прюитт, Б. Л. Конструкция сканирующих зондов с пьезорезистивным и пьезоэлектрическим контактным режимом.J. Micromechanics Microengineering 20, 095023 (2010).

ADS Статья Google Scholar

Минн, С. К., Маналис, С. Р. и Куэйт, К. Ф. Усовершенствование сканирующей зондовой микроскопии. Гл. 2.7, 42 (Springer, США, 1999).

Сарид Д. Сканирующая силовая микроскопия. Гл. 3.7, 46 (Oxford University Press, 1994).

Батт, Х.-Дж. И Яшке М. Расчет теплового шума в атомно-силовой микроскопии.Нанотехнологии 6, 1–7 (1995).

ADS Статья Google Scholar

Фукума Т. и Джарвис С. П. Разработка атомно-силового микроскопа с частотной модуляцией жидкость-среда с малошумящим датчиком отклонения для кантилеверов различных размеров. Rev. Sci. Instrum. 77, 043701 (2006).

ADS Статья Google Scholar

Bruker Nano Surfaces Division, Брошюра по атомно-силовому микроскопу Bruker MultiMode 8 (2011 г.) Доступно по адресу: https: // www.bruker.com/fileadmin/user_upload/8-PDF-Docs/SurfaceAnalysis/AFM/Brochures/B072-RevC0-MultiMode_8-Brochure__LoRes_.pdf (дата обращения: 26 августа 2015 г.).

Гарсия, Р. и Перес, Р. Методы динамической атомно-силовой микроскопии. Серфинг. Sci. Реп. 47, 197–301 (2002).

ADS Статья Google Scholar

Гарсия, Р. и Сан-Пауло, А. Притягивающие и отталкивающие режимы взаимодействия зонд-образец в атомно-силовой микроскопии в режиме постукивания.Phys. Ред. B 60, 4961–4967 (1999).

ADS Статья Google Scholar

Кокавец Дж., Хорват З. Л. и Мехлер А. Динамические свойства атомно-силового микроскопа с контролем добротности. Прил. Phys. Lett. 85, 3232–3234 (2004).

ADS CAS Статья Google Scholar

Adams, J. D. et al. Модернизация высокоскоростной визуализации для стандартного сканирующего атомно-силового микроскопа с использованием небольших кантилеверов.Rev. Sci. Instrum. 85, 093702 (2014).

ADS Статья Google Scholar

Гиссибл, Ф. Дж. Атомное разрешение на Si (111) — (7 × 7) с помощью бесконтактной атомно-силовой микроскопии с датчиком силы на основе кварцевого камертона. Прил. Phys. Lett. 76, 1470–1472 (2000).

ADS CAS Статья Google Scholar

Enning, R. et al. Высокочастотный датчик для атомно-силовой микроскопии оптического отклонения луча.Rev. Sci. Instrum. 82, 043705 (2011).

ADS Статья Google Scholar

Баргатин, И., Майерс, Э. Б., Арлет, Дж., Гудлевски, Б. и Роукс, М. Л. Чувствительное обнаружение наномеханического движения с использованием пьезорезистивного понижающего микширования сигнала. Прил. Phys. Lett. 86, 133109 (2005).

ADS Статья Google Scholar

Fantner, G.E. et al. Использование самодействующих и самочувствительных кантилеверов для визуализации биологических образцов в жидкости.Нанотехнологии 20, 434003 (2009).

CAS Статья Google Scholar

Aeschimann, L. et al. Матрицы сканирующих зондов для биологических наук и нанобиологии. Микроэлектрон. Англ. 83, 1698–1701 (2006).

CAS Статья Google Scholar

Nečas, D. & Klapetek, P. Gwyddion: программное обеспечение с открытым исходным кодом для анализа данных SPM. Cent. Евро. J. Phys.2012. Т. 10. С. 181–188.

Google Scholar

Gutsmann, T. et al. Силовая спектроскопия коллагеновых волокон для исследования их механических свойств и структурной организации. Биофиз. J. 86, 3186–3193 (2004).

ADS CAS Статья Google Scholar

Эксперимент по измерению прогиба консольной балки

Введение

1.Краткое описание
Пластиковое оптическое волокно прикреплено к балке (консольной) для контроля ее отклонения. Изменение силы света оптического волокна отслеживается с помощью светозависимого резистора (LDR) и базовой схемы делителя напряжения. Выходной сигнал LDR непрерывно измеряется ADC-16, и эта простая система может обеспечить мониторинг отклонения луча в реальном времени с помощью ПК.

2. Чему пытается научить эксперимент
Эксперимент подчеркивает потенциальную возможность использования оптического волокна в качестве датчика для отслеживания в реальном времени отклонения конструкции.Студенты также получат практический опыт построения базовой электрической схемы на основе простых устройств, таких как светозависимый резистор (LDR), считывание значений резисторов, принцип делителей напряжения и закон Ома.

3. Требуются предварительные знания
Студенты должны иметь представление о том, как оптическое волокно передает свет через свою сердцевину, а также о принципе полного внутреннего отражения (TIR) ​​и о влиянии чрезмерного изгиба на передачу света в этих световодах. СМИ.Во-вторых, учащиеся должны иметь представление о функции светозависимого резистора, принципах делителей напряжения и закона Ома.

4. Целевая группа
Этот эксперимент подходит для студентов, изучающих углубленную физику, и служит простым введением в практическое использование оптических, электронных и оптоэлектронных устройств.

Необходимое оборудование

• Оборудование для регистрации данных
• Светозависимый резистор (LDR)
• Светодиод (LED)
• резистор 1 кОм
• Паяльник
• А усилитель напряжения / сигнала (опция)
• 2 х 1.Батарейки 5 В (для питания светодиода) и 2 батареи по 9 В (для цепи делителя)
• Волоконно-оптические разъемы (многомодовые разъемы SMA)
• Оптоволоконный датчик
• Гибкая балка (например, пластиковая линейка)
• Клей быстрого отверждения

Предупреждение по безопасности: Хотя в целом работа с большинством маломощных светодиодов безопасна, по соображениям безопасности не смотрите прямо на светодиоды, когда они горят. Паяльник следует использовать только под присмотром.

Экспериментальная установка

На рисунке 1 показана экспериментальная установка для эксперимента.

Рисунок 1: Экспериментальная установка

Рисунок 1a: Схема делителя напряжения (в базовой схеме на Рисунке 1)

Экспериментальные схемы для испытаний на трехточечный изгиб и растяжение показаны на рисунке 4.Для питания светоизлучающего диода использовался стандартный источник напряжения. Детектор и система сбора данных состояла из светозависимого резистора (LDR) и недорогой коммерческой системы сбора данных от Pico Technology, которая автоматически регистрирует изменения напряжения на LDR в качестве интенсивность света варьируется. Система сбора данных предлагает аналого-цифровое преобразование (АЦП) с разрешением до 16 бит и до 8 входных каналов. Разрешающая способность системы АЦП позволяет обнаруживать изменения напряжения до 40 мВ в электрическом сигнале.Частота дискретизации 2 выборки данных в секунду будет достаточной для целей эксперимента. Данные с оптического волокна автоматически собирались компьютером и отображались графически в реальном времени.

Схема луча с привязанным оптоволоконным датчиком показана на рисунке 2. Подробности будут приведены в следующем разделе.

Рисунок 2: Схема образца пучка с волоконно-оптическим датчиком

При правильной настройке эксперимента балка должна изгибаться вокруг своего центра с нагрузкой, приложенной к центру опор, как показано на рисунке 3, где W — приложенная нагрузка, dctr — центральное отклонение.

Рисунок 3: Правильная установка балки

Проведение эксперимента

1. Прикрепите оптоволоконный датчик к балке (например, пластиковую линейку) с помощью суперклея или другого доступного клея и подождите, пока он высохнет. Убедитесь, что соединение надежно и что датчик не отклеивается, когда образец луча изгибается.
2. Подключите оптические разъемы к обоим концам оптического волокна и подключите их к светодиоду и LDR соответственно.Убедитесь, что они надежно соединены, чтобы свести к минимуму любые нежелательные изменения сигнала напряжения из-за потерь в соединении и шума окружающей среды.
3. Осторожно наденьте балку на опоры. Балку также можно закрепить на одном конце и освободить другой конец, как в консольной балке, в качестве альтернативной системы поддержки показанной.
4. Убедитесь, что PicoLog показывает выходное напряжение, чтобы убедиться в правильности настройки и готовности к началу испытания на отклонение луча.
5. Отрегулируйте масштаб оси Y графика в PicoLog для получения оптимального изображения.Если у вас есть усилитель сигнала, вы также можете настроить уровень напряжения, подаваемого на АЦП.
6. Медленно сделайте небольшое отклонение балки и наблюдайте за изменением уровня напряжения, отображаемым PicoLog. Сигнал увеличился или уменьшился при применении отклонения? В зависимости от чувствительности волокна можно ожидать изменения напряжения не менее 100 мВ для отклонения 10 мм при использовании показанной установки.
7. Теперь отпустите отклонение и наблюдайте за изменением уровня напряжения, показанным PicoLog.Что происходит с сигналом? Возвращается ли сигнал к исходному значению сигнала?
8. Теперь попробуйте с разной степенью отклонения и понаблюдайте за изменениями сигнала напряжения. Что вы заметили?

Вопросы

1. Не могли бы вы объяснить, как работает схема, обеспечивающая пропорциональный выходной сигнал при изменении интенсивности света оптоволоконного датчика?
2. Как вы думаете, что произойдет с сигналом напряжения, если луч будет отклонен вверх, а не вниз, как это делалось ранее?

Дальнейшее изучение

Динамический мониторинг с использованием оптоволоконных датчиков:
Важным аспектом мониторинга реальных инженерных сооружений является выполнение динамического анализа вибрирующих конструкций.Оптоволоконные датчики, основанные на вышеупомянутой системе, представляют собой рентабельный метод контроля динамической системы. В качестве дальнейшего исследования луч, использованный в вышеупомянутом эксперименте, может подвергаться непрерывному отклонению с помощью кулачка, прикрепленного к двигателю, обеспечивая постоянную скорость отклонения луча при отслеживании выходного сигнала оптического волокна. Другие типы АЦП, поставляемые Pico Technology Ltd, могут быть более подходящими для динамического мониторинга. Обратитесь в Pico Technology за советом.

Колебания консольных балок:

Колебания консольных балок:

Колебания консольных балок:

Отклонение, частота и использование в исследованиях

Для: Dr.Негахбан

EngrM 325H

Скотт Уитни

23 апреля 1999 г.

Введение

Измерение свойств тонкой пленки затруднено по сравнению с сыпучие материалы. Один из методов определения модуля упругости тонкого фильм взят из частотного анализа консольной балки. Прямая, горизонтальная консольная балка под действием вертикальной нагрузки деформируется в кривую.Когда это сила снимается, балка вернется в первоначальную форму; тем не мение, его инерция будет удерживать луч в движении. Таким образом, балка будет вибрировать на его характерные частоты. Если на луч напыляется тонкая пленка, изменится жесткость на изгиб. Это изменение вызывает частоту колебаний сдвинуть. Если сдвиг частоты измерен, пленки модуль упругости можно рассчитать.

Установка тонкой консольной балки

Балки, изучаемые в этой статье, представляют собой длинные, тонкие консольные балки.Фигура 1 ниже показана такая балка. Один конец балки закреплен, а другой конец свободен. Начало координатной оси находится на фиксированном конце, точка А . Типичная балка, использованная в этом исследовании, имеет длину L, = 30 мм, Вт = 5 мм шириной и т = 0,5 мм толщиной. Материал балки необходимо выбрать так что его жесткость отличается от жесткости тонких пленок, так что частотный сдвиг значительный. В данном исследовании использовались пленки оксида цинка (около Толщиной 5 м), поэтому хорошая подложка — алюминий.

Рисунок 1: Изученная типовая консольная балка

Прогиб консольной балки

Если свободный конец консольной балки подвергается точечной нагрузке, P , луч отклонится в кривую. См. Рисунок 2 ниже. Чем больше нагрузка, тем больше прогиб, (x) .

Рисунок 2: Прогиб консольной балки под нагрузкой на неподвижном конце

Предполагая, что балка претерпевает небольшие отклонения, находится в линейно-упругой области и имеет однородное поперечное сечение, следующие уравнения могут быть использовал (Гир, стр.602).

Кривизна балки ,, равна второй производной прогиба

Кривизна также может быть связана с изгибающим моментом, M , и жесткость на изгиб, EI, где E — модуль упругости балки, а I — момент инерции. Изгибающий момент в балке можно связать с поперечной силой, В , и боковая нагрузка на балку q .Таким образом, (1а, б, в) Для нагрузки, показанной на рисунке 2, распределенная нагрузка, поперечная сила и изгибающий момент составляет: Таким образом, решение уравнения (1a) есть

(2а)

На свободном конце балки смещение составляет: (2b) Колебания балок

-Определение уравнений

Когда сила P снимается со смещенной балки, балка вернется к своей первоначальной форме.Однако инерция балки вызовет луч, чтобы вибрировать вокруг этого исходного местоположения. Предполагая, что эластичный модуль, инерция и площадь поперечного сечения ( A ) постоянны вдоль длина балки, уравнение для этой вибрации (Volterra, стр. 310)

(3) где линейная массовая плотность балки. Уравнение (3) лучше всего решается разделением переменных (Аткинс, стр. A29). Предположим, что смещение можно разделить на две части, одна зависит от положения, а другая от времени. (х, t) = X (x) f (t) (4) где X не зависит от времени, а f не зависит от положения. Тогда уравнение (3) принимает вид

Деление уравнения (3) на X (x) f (t) : (5) Поскольку левая часть уравнения (5) не меняется при изменении t , правая часть должна быть постоянной. Аналогично, поскольку правая половина уравнения (5) не изменяется при изменении x , левая половина должна быть постоянной.Поскольку каждая сторона постоянна, уравнение (4) действительно и метод может использоваться разделение переменных. Обозначим эту постоянную. Можно показать, что это реальная величина, и что — собственные частоты балки.

Уравнение (5) теперь можно записать в виде двух дифференциальных уравнений (Вольтерра, п. 311),

(6а, б) где (6c) Чтобы решить уравнение (6a), следующие граничные условия для консольная балка необходима

Эти граничные условия исходят от опор консольной балки.Неподвижный конец должен иметь нулевое смещение и нулевой наклон из-за зажима. Свободный конец не может иметь изгибающий момент или усилие сдвига.

Общее решение уравнения (6a) представляет собой линейную комбинацию тригонометрических уравнения (Вольтерра, стр.312)

(7) Используя первое граничное условие, можно найти C ₁ => Взяв первую производную уравнения (7) и используя вторую границу состояние, C ₃ можно найти

=> Старшие производные уравнения (7) и остальные граничные условия дайте (8а) (8b)

Уравнения (8a) и (8b) можно объединить, чтобы получить

(9) Таким образом, для консольной балки уравнение (7) сводится к

(10)

Согласно Volterra, p.312, константы C _n равны произвольный. Однако для динамического решения смещения быть равным статическому решению (в момент времени t = 0), C ₂ должно быть равно ½. С этим значением для C ₂ , X _n (0) = 0 и X _n (L) = 1 .

Подстановка уравнения (9) в (8a) или (8b) приведет к определению частоты уравнение для консольной балки,

(11) Частотное уравнение может быть решено для постоянных: k _n L ; первые шесть показаны ниже на рисунке 3 (примечание, k _n = 0 игнорируется, поскольку это означает, что полоса находится в состоянии покоя, поскольку = 0).Эти константы вместе с уравнением (6c) можно использовать для нахождения естественного частоты консольной балки.

Рисунок 3: Константы колебаний консольной балки. Обратите внимание, поскольку cosh ( x ) большой, когда x большой, k _n L требуется быть найденным с высокой точностью.

Для каждой частоты существует характерная вибрация (Вольтерра, п. 319)

(12) где A _n зависит от начальной позиции в момент времени t = 0, и B _n зависит от начальной скорости.В этом исследовании, балка начинает вибрировать при смещении и в состоянии покоя. Таким образом, B _n = 0 а также (13) Начальное смещение, (x, 0) , было найдено выше, уравнение (2a). Уравнение (13) можно решить аналитически с помощью компьютерной математической программы,

-Примеры режимов вибрации

Типичные значения A _n и частоты (для используемых лучей в этом исследовании) показаны на Рисунке 3 выше.Обратите внимание, что только первый несколько режимов вибрации имеют значительно большие значения для постоянной А _№ . Таким образом, колебательными модами более высокого порядка можно пренебречь. Чтобы получить полное смещение консольной балки, просто сложите все смещения, найденные в уравнении (12) для каждой моды. Ниже на Рисунке 4 показано смещение, вызываемое каждой модой при т = 0; также включен полное начальное смещение балки. От этих перемещений это очевидно, что даже третья характеристическая мода мало влияет на полное перемещение балки.

Рисунок 4: Начальное смещение, вызванное каждой модой.

Со временем каждая мода будет колебаться вокруг нулевого смещения. линии с частотой, указанной на рисунке 3 выше. На рисунке 5 ниже показано эта вибрация для первых двух режимов, более высокие моды действуют аналогично. В общее движение луча сложное; каждая характеристическая мода колеблется с разного размера, формы и частоты.

Следующие файлы можно загрузить для просмотра анимации первого несколько режимов и полная вибрация консольной балки.Чтобы просмотреть их, необходимо загрузить Lotus Screencam Player: Scplayer.exe

Общее движение: 325Htot.exe
1-й режим: 325h2st.exe
2-й режим: 325h3nd.exe
3-й режим: 325h4rd.exe
4-й режим: 325h5th.exe

На рисунке 6 ниже показаны показания пьезоэлектрического датчика, расположенного возле закрепленного конца балки; этот датчик показывает взаимодействие каждого режим вибрации.Также показана вибрация, предсказанная из уравнения (12). в этом месте. Фактические и прогнозируемые сигналы почти идентичны; основное различие между ними — демпфирование (как вязкое, так и Кельвина-Фойгта) колебаний высших порядков в реальном сигнале.

Рисунок 5: Колебания первых двух характерных мод; другие режимы вибрировать аналогично. Время t в микросекундах.

Рисунок 6: Сигнал ZnO от вибрирующей консольной балки по сравнению с теоретические колебания.

Измерение модуля упругости для тонких пленок

-Причина использования частотного анализа

Если консольная балка покрыта напылением тонкой пленки, то изгиб изменится жесткость. Изменение жесткости напрямую повлияет на частоту колебаний балок. Таким образом, модуль упругости пленки может быть определяется из этого сдвига частоты. См. Рисунок 7 для схематического рисунка. напыленного пучка; индекс s относится к подложке, а f относится к фильму.Обратите внимание, высота пленки сильно преувеличена, поскольку .

Рисунок 7: Распылитель консольной балки, покрытый тонкой пленкой

Теоретически жесткость можно определить по неподвижной балке. под нагрузкой, P , см. уравнения (2a, b). Предположим, что жесткость на изгиб был увеличен добавлением тонкой пленки к лучу. Тогда, если предположить, что нагрузка была постоянной, прогиб на свободном конце уменьшится.Для Типичная балка, описанная выше, это изменение смещения чрезвычайно мало. Например, алюминиевая балка с начальным смещением (на свободном конце) 0,55 мм будет иметь начальное смещение 0,49 мм при относительно толстый (8 м) ZnO фильм. Изменение 0,06 мм слишком мало, чтобы его можно было измерить обычным инструменты и более тонкая пленка ZnO (1 м) даст неизмеримую разницу в смещении. Таким образом, стационарный измерения модуля упругости пленок затруднены, если не невозможно.

Однако тот же луч, покрытый ZnO, будет иметь свою основную частоту, сдвиг с 329,7 Гц на 342,0 Гц. Любой осциллограф можно использовать для измерения колебания балок, см. рисунок 6 выше. Если будет взято достаточно точек данных, преобразование Фурье сигнала может измерять частотные сдвиги, даже если малая как 0,2 Гц. Следовательно, сдвиг частоты может быть известен с помощью высокая точность, и можно рассчитать модуль упругости пленок.

-Определение уравнений

Все уравнения, полученные в предыдущих разделах (1-13), все еще могут применяется к двухкомпонентной балке при изменении нескольких постоянных: EI заменяется на E _s I _s + E _f I _f и исправлено как показано ниже.Заявленные ранее предположения все еще должны выполняться: небольшие прогибы, линейно-упругие и однородное поперечное сечение. Последний Из этого предположения следует, что толщина пленки не может меняться вдоль луча (сложная делать при напылении покрытия длинных балок).

Линейная массовая плотность балки с покрытием теперь равна

Центр масс, а также инерция балки с покрытием сместятся

Уравнение (6c) используется для измерения модуля упругости пленки. от сдвига частоты.(14)

(15)

Поскольку амплитуды более высоких мод колебаний настолько малы, см. Рис. 4 уравнение (15) решается с использованием основной частоты n = 1.

Заключение

Из-за небольшого размера тонких пленок обычные методы измерения их свойства часто не работают. Эти свойства тонкой пленки могут отличаться. от свойств сыпучего материала. Поэтому альтернативные методы измерения должны быть развиты.Вибрация консольных балок — один из таких методов.