Определите угол: Угол — Википедия – Углы треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Определение угла | Треугольники

Что такое угол? Введём определение угла.

Определение.

Угол — это геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.

Лучи называются сторонами угла, а их общее начало — вершиной угла.

Например, вершина угла BAC — точка A, стороны — лучи AB и AC.

Знак угла — ∠ — представляет собой уменьшенное изображение угла.

Запись «∠ABC» читают как «угол ABC».

Угол можно назвать одной или тремя буквами. Если буква одна, то это — вершина угла. Если букв три, то вершина вершина должна стоять посередине, а по бокам — точки, лежащие на сторонах угла:

∠B или ∠ABC или ∠CBA.

Другой способ определить угол: по названию лучей — сторон угла.

∠(a; b) — угол, стороны которого — лучи a и b.

Обозначают угол дужкой.

Два угла называются равными, если они могут быть совмещены так, что совпадут их соответствующие стороны и вершины.

 

∠BAC=∠MNK.

Равные углы обозначают равным количеством дужек.

Единицы измерения углов — градусы и радианы.

1 градус (1º) равен 1/180 доле развёрнутого угла.

Градусную меру угла измеряют с помощью транспортира.

1 радиан — величина центрального угла, опирающегося на дугу окружности, равной её радиусу.

Наглядное представление об угле в 1 радиан можно получить, если отрезать кусок нити длиной, равной радиусу окружности, и приложить эту нить к окружности. Центральный угол, опирающийся на полученную дугу, — это и есть угол в один радиан:

 

∠ABC=1 радиану

 

1 радиан ≈ 57º,   π радиан=180º.

Основные свойства измерения углов:

Каждый угол имеет определённую градусную меру, большую нуля.

Развёрнутый угол равен 180 градусам.

Градусная мера угла равна сумме градусных мер углов, на которые они разбиваются любым лучом, проходящим между его сторонами.

 

Иногда угол определяют как часть плоскости, заключённую между двумя лучами с общим началом.

В тех случаях, когда угол рассматривают как меру поворота луча вокруг его начала до заданного положения, величина угла может принимать любые значения, в зависимости от направления поворота как положительные, так и отрицательные.

Как определить натуральную величину угла

Чтобы определить натуральную величину угла, нужно перевести его в положение, в котором его стороны будут параллельны плоскости проекции. Наиболее рациональный путь решения данной задачи – использовать способ вращения вокруг линии уровня. Более трудоемкими вариантами являются метод замены плоскостей проекций и параллельное перемещение.

Задача

Приведенный ниже пример иллюстрирует нахождение угла между пересекающимися прямыми m и n способом вращения вокруг фронтали.

Последовательность построений:

1. В произвольном месте чертежа проводим фронталь f. Она пересекает прямые m и n в точках 1 и 2. Определяем их недостающие проекции.
2. Через точку K» проводим перпендикуляр к f». На пересечении этого перпендикуляра с фронталью находится проекция центра вращения O». По линии связи определяем положение т. O’.
3. Находим величину радиуса R поворота точки K. Для этого перпендикулярно O»K» откладываем отрезок K»K₀ = y_k – y_o. Таким образом, R равен O»K₀ – гипотенузе прямоугольного треугольника O»K»K₀.
4. Проводим дугу радиусом R до её пересечения с перпендикуляром O»K» в точке K»₁
   . Соединяем K»₁ c точками 1» и 2». Натуральная величина угла между прямыми m и n равна углу ϕ при вершине K»₁.

Более подробную информацию о методе вращения вокруг линии уровня, который мы здесь использовали, вы можете найти на следующей странице.

Определение угла между скрещивающимися прямыми

Углом между скрещивающимися прямыми называют плоский угол, стороны которого параллельны данным прямым. На изображении, приведенном ниже, прямые e и d скрещивающиеся и друг с другом не пересекаются. Чтобы найти угол между ними, выполним ряд графических построений:

Описание решения

• На любом свободном месте чертежа отмечаем точку S. Располагаем её произвольно (проекции S» и S’ показаны на рисунке).
• Через точку S проводим прямые a и b так, чтобы они были параллельны e и d. В нашем случае a||e, b||d соответственно.
• Строим горизонталь h, которая будет играть роль оси вращения. Перпендикулярно h’ из точки S’ проводим прямую. Она пересекает h’ в т. O’ – горизонтальной проекции центра вращения.
• Определяем радиус поворота R как гипотенузу треугольника O’S’S₀. При этом катет S’S₀ равен разности удаления точек S» и O» от горизонтальной плоскости.
• Находим т. S’₁ на пересечении дуги радиуса R с прямой S’O’. Соединяем S’₁ c точками 1′ и 2′, которые своего положения не меняют. Угол ϕ при вершине S’₁ искомый. Задача решена.

Похожие задачи:

Угол между пересекающимися прямыми: определение, примеры нахождения

Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.

Что такое угол между пересекающимися прямыми

Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.

Определение 1

Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.

Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.

Допустим, нам известно, что один из углов равен α. В таком случае угол, который является вертикальным по отношению к нему, тоже будет равен α. Чтобы найти оставшиеся углы, нам надо вычислить разность 180°-α. Если α будет равно 90 градусам, то все углы будут прямыми. Пересекающиеся под прямым углом линии называются перпендикулярными (понятию перпендикулярности посвящена отдельная статья).

Взгляните на рисунок:

Перейдем к формулированию основного определения.

Определение 2

Угол, образованный двумя пересекающимися прямыми – это мера меньшего из 4-х углов, которые образуют две эти прямые.

Из определения нужно сделать важный вывод: размер угла в этом случае будет выражен любым действительным числом в интервале (0, 90]. Если прямые являются перпендикулярными, то угол между ними в любом случае будет равен 90 градусам.

Как найти угол между пересекающимися прямыми на плоскости

Умение находить

Определение угол общее значение и понятие. Что это такое угол

Понятие угла, которое происходит от латинского слова angŭlus, относится к фигуре геометрии, которая образована из двух линий, которые пересекаются друг с другом на одной поверхности. Можно также сказать, что угол образован двумя лучами, которые имеют одну и ту же вершину.

Углы могут быть измерены в разных единицах : полугодовая степень и радиан являются наиболее частыми измерениями. Согласно этому измерению углы классифицируются по-разному.

Если мы помещаем себя в поле шестигранных градусов, то прямой угол, например, составляет 90 °. Если угол составляет менее 90 °, но больше 0 °, он классифицируется как острый . С другой стороны, если он измеряет более 90 ° и менее 180 °, его называют тупым углом .

Единицей, которая впервые преподается в школе, является шестнадцатеричная оценка по полу, поскольку ее легче понять: с помощью измерительного инструмента, такого как транспортир, мы должны определить угол раскрытия и присвоить ему соответствующее значение аналогичным образом. к тому, что мы делаем при измерении протяженности объекта в сантиметрах. Тем не менее, радиан является гораздо более полезным и используется преимущественно в научной среде.

Чтобы выполнить измерение угла в радианах, мы должны продолжить его дугу до завершения воображаемого круга, в центре которого находится вершина первого; Другими словами, мы можем думать о торте, в котором не хватает порции, это угол измерения. Значение 1 радиан эквивалентно дуге, длина которой, в свою очередь, равна длине радиуса рассматриваемой окружности; половина окружности равна π (pi) радиан, а 2π радиан — полная окружность. Чтобы преобразовать значение в шестнадцатеричных градусах в радианы, нужно умножить его на пи и разделить на 180.

Нулевой угол, плоский угол, вогнутый угол и полный угол — некоторые из наиболее распространенных типов. Также, принимая другие характеристики, мы можем говорить о смежных углах, дополнительных углах, дополнительных углах, внешних углах, внутренних углах и телесных углах .

В области развития компьютерной графики, которая охватывает различные виды современных развлечений, таких как кино и видеоигры, концепция ракурса является одной из наиболее актуальных, поскольку она возникает в различных ситуациях: с точки зрения камеры. направление, в котором перемещается объект, вращение различных частей анимированной модели, столкновения между двумя объектами (например, землей и персонажем или двумя персонажами) и влияние ветра на сцену таковы. только несколько примеров.

В отличие от других операций, таких как сложение и умножение, вычисление, необходимое для определения значения угла, относительно требовательно для процессора, а также для вычисления квадратного корня, и поэтому программисты должны находить «экономичные» методы для избежать перегрузки во время выполнения; Очень распространенным решением является вычисление всех необходимых значений во время загрузки программы, чтобы составить список, к которому можно без проблем обращаться.

За пределами геометрии идея угла часто используется для обозначения угла или угла : «Я думаю, мы могли бы поставить новую библиотеку под этим углом», «Ваза бабушки сияет в углу столовой. ».

Угол, с другой стороны, является перспективой или точкой зрения . Говорят, что человек наблюдает реальность в соответствии с особым и особенным взглядом, известным как ракурс: «С моей точки зрения, опыт — это самая важная вещь для успешного выполнения такого рода задач».

Угол между прямыми

Определение угла между прямыми

Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.

Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

Если две прямые заданы уравнениями с угловым коэффициентом

y = k₁x + b₁,
y = k₂x + b₂,

то угол между ними можно найти, используя формулу:

tg γ = k₁ — k₂1 + k₁·k₂

Если знаменатель равен нулю (1 + k₁·k₂ = 0), то прямые перпендикулярны.

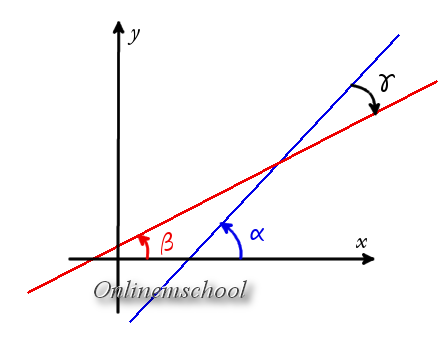Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX

tg α = k₁
tg β = k₂

Соответственно легко найти угол между прямыми

γ = α — β

tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k₁ — k₂1 + k₁·k₂

Угол между прямыми через направляющие векторы этих прямых

Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано параметрически

x = l t + ay = m t + b

то вектор направляющей имеет вид {l; m}

Если уравнение прямой задано как

A x + B y + C = 0

то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m

то вектор направляющей имеет вид {l; m}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}

Угол между прямыми через векторы нормалей этих прямых

Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано как

A x + B y + C = 0

то вектор нормали имеет вид {A; B}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то вектор нормали имеет вид {1; -k}

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

sin φ = |a · b||a| · |b|

Примеры задач на вычисления угла между прямыми на плоскости

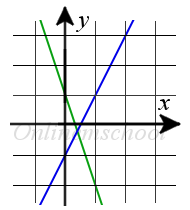Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ = k₁ — k₂1 + k₁·k₂ = 2 — (-3)1 + 2·(-3) = 5-5 = 1

Ответ. γ = 45°

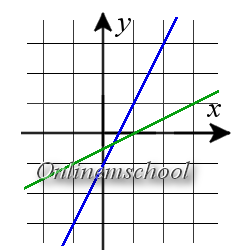Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}

cos φ = |1 · 2 + 2 · 1|1² + 2² · 2² + 1² = 45 · 5 = 0.8

Ответ. φ ≈ 36.87°

Пример 3 Найти угол между прямыми 2x + 3y = 0 и x — 23 = y4.

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2x + 3y = 0 => y = -23x   (k₁ = -23)

x — 23 = y4 => y = 43x — 83   (k₂ = 43)

tg γ = k₁ — k₂1 + k₁·k₂ = -23 — 431 + (-23)·43 = -631 — 89 = 18

Ответ. γ ≈ 86.82°

Угол между прямыми в пространстве

Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m = z — z₀n

то направляющий вектор имеет вид {l; m; n}

Если уравнение прямой задано параметрически

x = l t + ay = m t + bz = n t + c

то направляющий вектор имеет вид {l; m; n}

Пример 4. Найти угол между прямыми x = 2t + 1y = tz = -t — 1 и x = t + 2y = -2t + 1z = 1.

Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0|2² + 1² + (-1)² · 1² + (-2)² + 0² = 06 · 5 = 0

Ответ. φ = 90°

Пример 5 Найти угол между прямыми x — 23 = y4 = z — 35 и -x — 22 = 1 — 3y = 3z — 52.

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.

Преобразуем второе уравнение к каноническому вид.

-x — 22 = x — 2-2

1 — 3y = 1 + y-1/3 = y — 1/3-1/3

3z — 52 = z — 5/32/3

Получено уравнение второй прямой в канонической форме

x — 2-2 = y — 1/3-1/3 = z — 5/32/3

{-2; -13; 23} — направляющий вектор второй прямой.

cos φ = 3·(-2) + 4·(-13) + 5·233² + 4² + 5² · (-2)² + (-13)² + (23)² = -6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49 = -450 · 41/9 = 12582 = 682205

Ответ. φ ≈ 74.63°

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Вписанные и центральные углы

      Определение 1. Центральным угломназывают угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Рис. 1

      Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Рис. 2

      Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

      Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.

Теоремы о вписанных и центральных углах

Фигура	Рисунок	Теорема
Вписанный угол		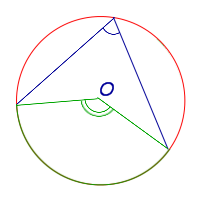Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанный угол		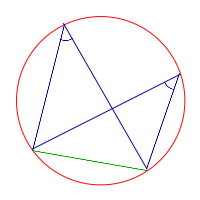Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Вписанный угол		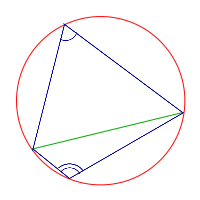Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды
Вписанный угол		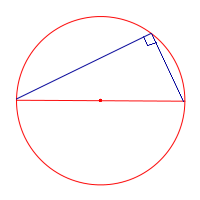Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Окружность, описанная около прямоугольного треугольника		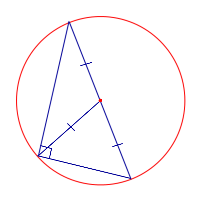Середина гипотенузы прямоугольного треугольника является центром описанной около этого треугольника окружности. Посмотреть доказательство

Вписанный угол

Теорема: Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство

Теорема: Вписанные углы, опирающиеся на одну и ту же дугу равны.

Теорема: Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Теорема: Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды

Теорема: Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Окружность, описанная около прямоугольного треугольника

Теорема: Середина гипотенузы прямоугольного треугольника является центром описанной около этого треугольника окружности. Посмотреть доказательство

Теоремы об углах, образованных хордами, касательными и секущими

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами		Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство
Угол, образованный секущими, которые пересекаются вне круга		Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство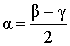
Угол, образованный касательной и хордой, проходящей через точку касания		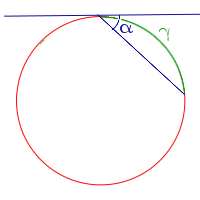Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство
Угол, образованный касательной и секущей		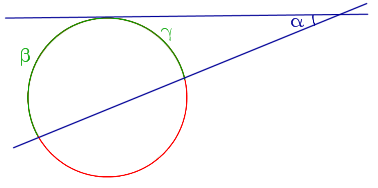Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство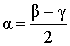
Угол, образованный двумя касательными к окружности		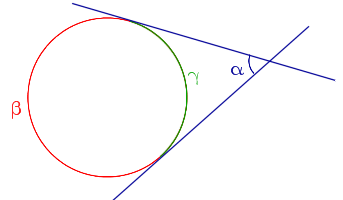Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство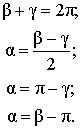

Угол, образованный пересекающимися хордами хордами

Формула:

Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство

Угол, образованный секущими секущими, которые пересекаются вне круга

Формула: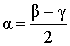

Теорема Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Угол, образованный касательной и хордой хордой, проходящей через точку касания

Формула:

Теорема Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство

Угол, образованный касательной и секущей касательной и секущей

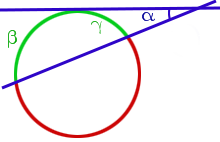Формула: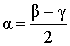

Теорема Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Угол, образованный двумя касательными касательными к окружности

Формулы: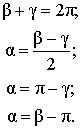

Теорема Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Доказательства теорем об углах, связанных с окружностью

      Теорема 1. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

      Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является диаметром окружности диаметром окружности, и центральный угол AOC (рис. 5).

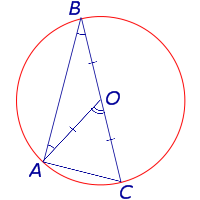
Рис. 5

      Так как отрезки AO и BO являются радиусами окружности радиусами окружности, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является внешним углом треугольника AOB, то справедливы равенства

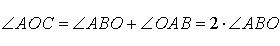
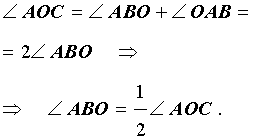
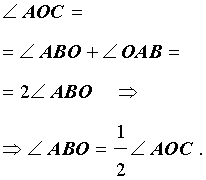
      Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

      Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

Рис. 6

      В этом случае справедливы равенства

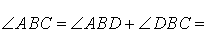
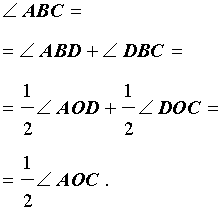
и теорема 1 в этом случае доказана.

      Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

Рис. 7

      В этом случае справедливы равенства

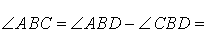
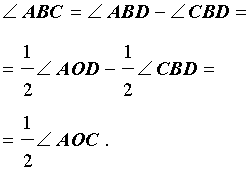
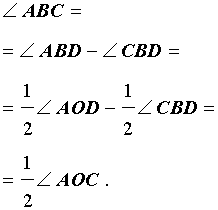
что и завершает доказательство теоремы 1.

      Теорема 2. Величина угла, образованного пересекающимися хордами хордами, равна половине суммы величин дуг, заключённых между его сторонами.

      Доказательство. Рассмотрим рисунок 8.

Рис. 8

      Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – внешний угол треугольника BED, а углы CDB и ABD являются вписанными углами, то справедливы равенства

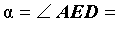
что и требовалось доказать.

      Теорема 3. Величина угла, образованного секущими секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

      Доказательство. Рассмотрим рисунок 9.

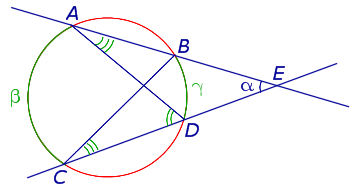
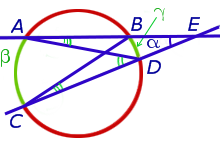
Рис. 9

      Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – внешний угол треугольника ADE, а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

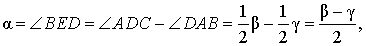
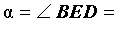
что и требовалось доказать.

      Теорема 4. Величина угла, образованного касательной и хордой касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

      Доказательство. Рассмотрим рисунок 10.

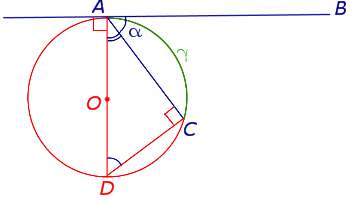
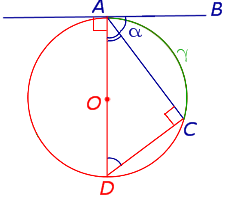
Рис. 10

      Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр, проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

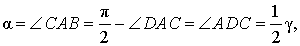
что и требовалось доказать

      Теорема 5. Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.

      Доказательство. Рассмотрим рисунок 11.

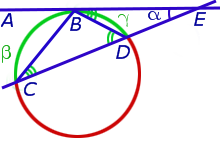
Рис. 11

      Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – внешний угол треугольника DBE, а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB, в силу теоремы 4, равны. Поэтому справедливы равенства

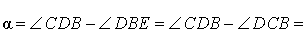
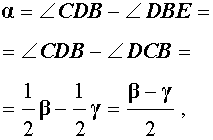
что и требовалось доказать.

      Теорема 6.Величина угла, образованного двумя касательными к окружности касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами.

      Доказательство. Рассмотрим рисунок 12.

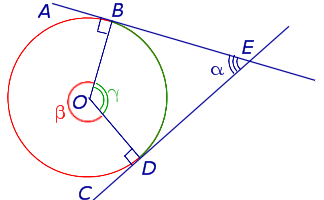
Рис. 12

      Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что углы BOD и BED в сумме составляют   π радиан. Поэтому справедливо равенство

α = π – γ .

      Далее получаем

что и требовалось доказать.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Определение угол общее значение и понятие. Что это такое угол

Понятие угла, которое происходит от латинского слова angŭlus, относится к фигуре геометрии, которая образована из двух линий, которые пересекаются друг с другом на одной поверхности. Можно также сказать, что угол образован двумя лучами, которые имеют одну и ту же вершину.

Углы могут быть измерены в разных единицах : полугодовая степень и радиан являются наиболее частыми измерениями. Согласно этому измерению углы классифицируются по-разному.

Если мы помещаем себя в поле шестигранных градусов, то прямой угол, например, составляет 90 °. Если угол составляет менее 90 °, но больше 0 °, он классифицируется как острый . С другой стороны, если он измеряет более 90 ° и менее 180 °, его называют тупым углом .

Единицей, которая впервые преподается в школе, является шестнадцатеричная оценка по полу, поскольку ее легче понять: с помощью измерительного инструмента, такого как транспортир, мы должны определить угол раскрытия и присвоить ему соответствующее значение аналогичным образом. к тому, что мы делаем при измерении протяженности объекта в сантиметрах. Тем не менее, радиан является гораздо более полезным и используется преимущественно в научной среде.

Чтобы выполнить измерение угла в радианах, мы должны продолжить его дугу до завершения воображаемого круга, в центре которого находится вершина первого; Другими словами, мы можем думать о торте, в котором не хватает порции, это угол измерения. Значение 1 радиан эквивалентно дуге, длина которой, в свою очередь, равна длине радиуса рассматриваемой окружности; половина окружности равна π (pi) радиан, а 2π радиан — полная окружность. Чтобы преобразовать значение в шестнадцатеричных градусах в радианы, нужно умножить его на пи и разделить на 180.

Нулевой угол, плоский угол, вогнутый угол и полный угол — некоторые из наиболее распространенных типов. Также, принимая другие характеристики, мы можем говорить о смежных углах, дополнительных углах, дополнительных углах, внешних углах, внутренних углах и телесных углах .

В области развития компьютерной графики, которая охватывает различные виды современных развлечений, таких как кино и видеоигры, концепция ракурса является одной из наиболее актуальных, поскольку она возникает в различных ситуациях: с точки зрения камеры. направление, в котором перемещается объект, вращение различных частей анимированной модели, столкновения между двумя объектами (например, землей и персонажем или двумя персонажами) и влияние ветра на сцену таковы. только несколько примеров.

В отличие от других операций, таких как сложение и умножение, вычисление, необходимое для определения значения угла, относительно требовательно для процессора, а также для вычисления квадратного корня, и поэтому программисты должны находить «экономичные» методы для избежать перегрузки во время выполнения; Очень распространенным решением является вычисление всех необходимых значений во время загрузки программы, чтобы составить список, к которому можно без проблем обращаться.

За пределами геометрии идея угла часто используется для обозначения угла или угла : «Я думаю, мы могли бы поставить новую библиотеку под этим углом», «Ваза бабушки сияет в углу столовой ».

Угол, с другой стороны, является перспективой или точкой зрения . Говорят, что человек наблюдает реальность в соответствии с особым и особенным взглядом, известным как ракурс: «С моей точки зрения, опыт — это самая важная вещь для успешного выполнения такого рода задач».