Несущая способность металлической балки — Доктор Лом. Первая помощь при ремонте
Несущая способность однопролетной металлической балки при равномерно распределенной нагрузке и шарнирном закреплении на опорах
1. Например, мы в качестве балок ддя перекрытия помещения размерами 4 на 6 метров использовали 4 профильных трубы сечением 100х100 мм с толщиной стенки 5 мм. Тогда длина пролета балки составит l = 4 м, а шаг балок 6/5 = 1.2 м. Согласно сортаменту для квадратных профильных труб момент сопротивления такой металлической балки составит Wz = 54.19 см3.
2. Расчетное сопротивление стали следует уточнять у производителя, ну а если оно точно не известно, то можно принимать наименьшее из возможных, т.е. R = 2000 кг/см2.
3. Тогда максимальный изгибающий момент, который может выдержать такая балка:
M = WzR = 54.19·2000 = 108380 кгсм или 1083.8 кгм.
4. При пролете 4 м максимальная распределенная нагрузка на погонный метр составляет:
q = 8M/l2 = 8·1083.8/42 = 541.9 кг/м.
5. При шаге балок 1.2 м (расстоянии между осями балок) максимальная плоская равномерно распределенная нагрузка на квадратный метр составит:
q = 541.9/1.2 = 451.6 кг/м2 (сюда входит и вес балок).
Вот и весь расчет.
Несущая способность однопролетной металлической балки при действии сосредоточенных нагрузок и шарнирном закреплении на опорах
Если на металлические балки перекрытия сверху уложены сначала лаги, а потом уже делается перекрытие по лагам, то на такие металлические балки будет действовать не одна равномерно распределенная нагрузка, а несколько сосредоточенных. Впрочем перевести сосредоточенные нагрузки в эквивалентную равномерно распределенную совсем не сложно — достаточно просто разделить значение равномерно распределенной нагрузки, которую мы уже определили, на коэффициент перехода.
Например, если мы по металлическим балкам уложили лаги через каждые 0.5 метра, то есть всего 4/0.5 +1 = 9 лаг — сосредоточенных нагрузок. При этом крайние лаги можно вообще в расчет не брать и тогда количество сосредоточенных сил будет = 7, а коэффициент перехода от сосредоточенных нагрузок к эквивалентной равномерно распределенной составит γ = 1.142.
Тогда максимальная равномерно распределенная нагрузка, которую может выдержать данная металлическая балка, составит:
q = 451.6/1.142 = 395.4 кг/м2
Конечно же металлические балки могут быть и многопролетными или иметь жесткое закрепление на одной или двух опорах, т.е. быть статически неопределимыми. В таких случаях изменится только формула определения максимального изгибающего момента (см. расчетные схемы для статически неопределимых балок), но весь алгоритм расчета останется таким же.
Определение несущей способности железобетонной балки
Определение несущей способности ж/б балки без арматуры в сжатой зоне
Дано:
железобетонная балка длиной 4.5 м, высотой h = 30 см, шириной b = 240 мм из бетона марки М300, что соответствует классу В22.5. Балка армирована арматурой класса А-III (A400), двумя стержнями диаметром 18 мм снизу. В качестве крупного заполнителя использовался гранитный щебень (в итоге имеем тяжелый бетон)
Требуется определить:
какую равномерно распределенную нагрузку выдержит такая балка при условии шарнирного закрепления на опорах.
Решение:
Алгоритм расчета в этом случае выглядит следующим образом: сначала определяется высота сжатой зоны бетона, затем — значение момента, а после этого можно определить значение нагрузки. Ну а теперь подробнее:
1. Определение пролета балки
Так как длину опорных участков балки желательно принимать не менее h/2, то в нашем случае расчетный пролет составит l = 4.5 — 0.3 = 4.2 метра.
2. Определение прочностных характеристик
Расчетное сопротивление арматуры растяжению мы можем сразу принять по соответствующей таблице Ra = 3600 кг/см2. В таблицах расчетное сопротивление бетона класса В22.5 не приводится. Однако ничего не мешает нам определить это значение интерполированием:
Rb = (11.5 + 14.5)/2 = 13 МПа или 13/0.0981 = 132.5 кг/см2
а с учетом различных коэффициентов, учитывающих возможную длительность действия нагрузки, повторяемость нагрузок, условия работы бетона и др. мы для надежности примем Rb = 132.5·0.8 = 106 кг/см2.
Два стержня арматуры диаметром 18 мм имеют площадь Аs = 5.09 см2. Это можно определить как непосредственно из формулы А = пd2/4, так и по таблице.
3. Определение относительной высоты ho
Если ho нам не известно, то из конструктивных соображений в данном случае защитный слой бетона а ≥ 1.8 см, соответственно h
4. Определение высоты сжатой зоны бетона
Согласно формуле 220.6.5 высота сжатой зоны у составляет
(6.5)
тогда
у = 3600·5.09/(106·24) = 7.2024 ≈ 7.2 см
Заодно определим, находится ли данное значение в пределах допустимого
у/ho ≤ ξR
7.2/27 = 0.267 < ξR = 0.531 (для арматуры класса А400)
5. Определение максимального значения момента
Так как согласно формуле 220.6.3
M < Rbbу (h0 — 0,5у)
То значение момента составит
М < 106·24·7.2(27 — 0.5·7.2) = 428613.12 кгс·см
т.е. максимально допустимое значение изгибающего момента составит M = 4286 кгс·м
6. Определение равномерно распределенной нагрузки
Так как
М = ql2/8
то
q = 8M/l2 = 8·4286/4.22 = 1943.46 кг/м
Т.е. имеющаяся балка при условии того, что при ее проектировании и изготовлении были соблюдены все конструктивные и технологические требования может выдерживать нагрузку до 1943 кг/м. Если на балку будут действовать одна или несколько сосредоточенных сил, то заключительная часть расчета будет несколько другой. Тем не менее часто сосредоточенную нагрузку или нагрузки можно привести к эквивалентной равномерно распределенной.
А если в сжатой зоне сечения также имеется арматура и ее влияние на прочность хочется учесть, то алгоритм расчета при этом не меняется, лишь немного усложняются формулы:
Определение несущей способности ж/б балки с арматурой в сжатой зоне
Например у рассчитанной выше балки имеется арматура в сжатой зоне — 2 стержня арматуры диаметром 12 мм. Площадь сечения сжимаемой арматуры составит А’s = 2.26 см2. Расстояние от верха балки до центра тяжести сжатой арматуры примем равным a’ = 3 см. Расчетное сопротивление сжатию составляет Rsc = 3600 кг/см2
При наличии арматуры в сжатой зоне формула для определения высоты сжатой зоны примет следующий вид:
(282.5)
тогда
у = 3600(5.09 — 2.26)/(106·24) = 4 см
так как у нас у/ho < ξR, то значение максимального изгибающего момента мы будем производить по следующей формуле:
M < Rbby(hо — 0,5у) +RcsA’s(ho — a’) (281.5.2)
M < 106·24·4(27 — 2) + 3600·2.26(27 — 3) = 254400 + 193536 = 447936 кгс·см
Таким образом максимально допустимое значение момента составит примерно М = 4479 кгс·м, т.е. примерно на 4.5% больше, чем при расчете без учета арматуры в сжатой зоне. Соответственно и значение максимально допустимой нагрузки также увеличится на 4.5% или в 1.045 раза и составит
q = 1943.46·1.045 = 2031 кг/м
Вот собственно и весь расчет. При этом стоит ли при расчете учитывать наличие арматуры в сжатой зоне сечения или нет — решать вам.
Несущая способность — балка — Большая Энциклопедия Нефти и Газа, статья, страница 1
Несущая способность — балка
Cтраница 1
Несущая способность балки будет исчерпана, когда напряжения достигнут предела текучести по всему сечению. [1]
Несущая способность балки будет исчерпана после образования второго пластического шарнира на опоре В, так как балка станет геометрически изменяемой. [2]
Несущая способность балки будет исчерпана, когда напряжения достигнут предела текучести по всему сечению. В этом случае От / граст т гсж и нейтральная ось делит площадь сечения пополам. Так как площадь стенки швеллера 36 — 0, 75 27 еж2 больше половины сечения 53, 4 / 2 26, 7 см2, то нейтральная ось проходят по площади стенки на расстоянии х от верхнего края. [3]
Несущая способность балок в общем случае изгиба при расчете их по методу расчетных предельных состояний обычно определяется по тем же формулам, что и при чистом изгибе. Касательные напряжения при этом могут вычисляться по методу, изложенному выше. [4]
Несущая способность балки, усиленной шпренгелем, должна проверяться на сочетаниях нагрузок, действующих на балку в момент установки шпренгеля ( усилия от натяжения и фактическая нагрузка) и на максимально возможную нагрузку после усиления. [5]
Несущая способность балки должна удовлетворять большему из двух указанных условий, обеспечивающих несущую способность усиленной конструкции по моменту и поперечной силе. [7]
Несущую способность балки
Несущую способность балки не-обходимо сопоставлять с величиной критического момента МКр, при котором наступает потеря устойчивости. Если Мкр меньше несущей способности, тогда М [ из уравнения ( 91) ] является решающим. [11]
Увеличение несущей способности балки при предварительном напряжении может быть оценено следующим образом. Сила Р создает в нижнем поясе напряжение т — aR, где a — коэффициент; R — расчетное сопротивление. [13]
Чем определяется несущая способность балки. [14]
После этого несущая способность балки исчерпана. [15]
Страницы: 1 2 3 4
3.2 Проверка несущей способности балки
А. Проверка прочности балки
Проверку на прочность выполняют по следующим формулам /1/:
в
сечениях с 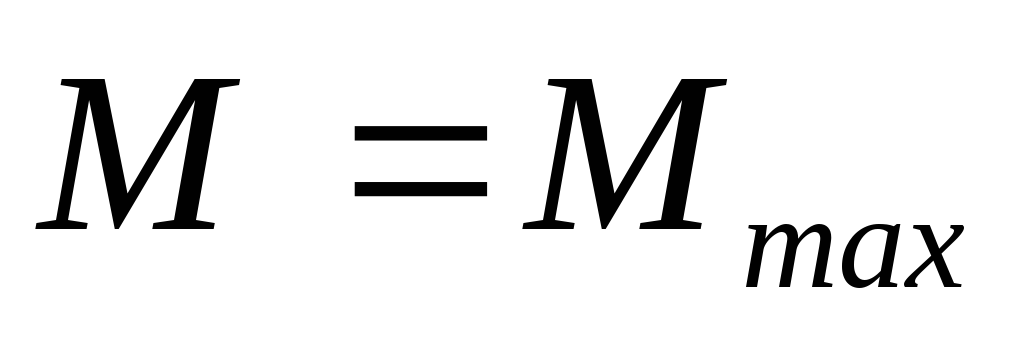
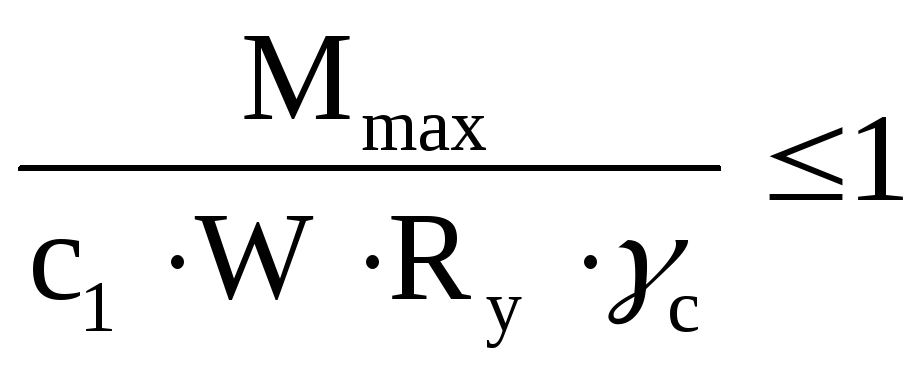 ;
(3.6)
;
(3.6)
в
сечениях с 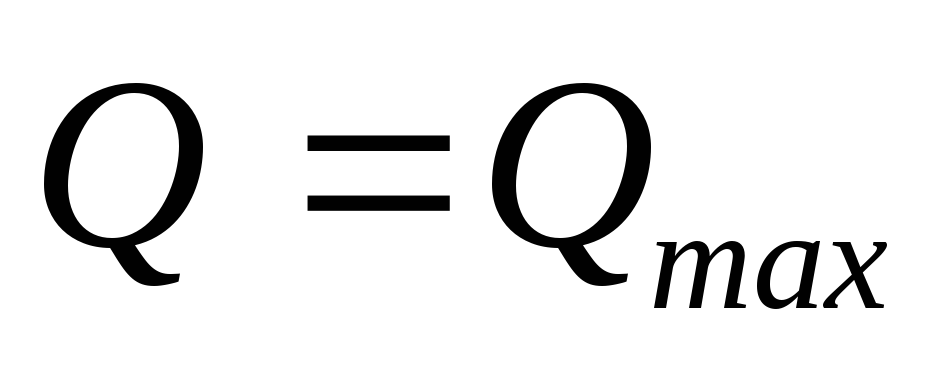
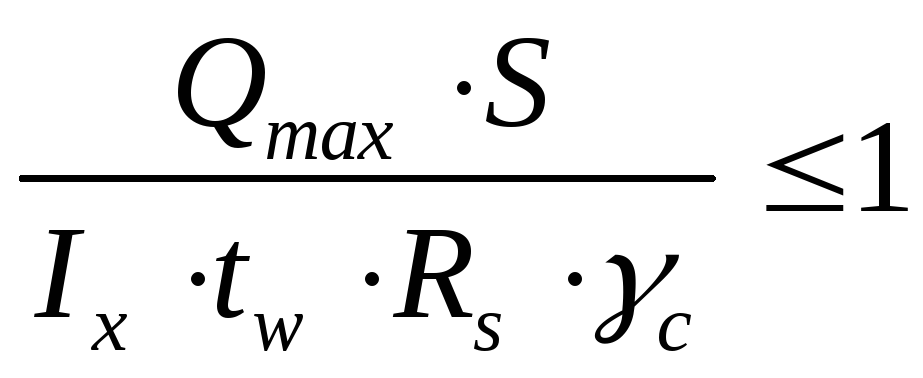 .
(3.7)
.
(3.7)
где  — наибольшая поперечная сила на опоре;
— наибольшая поперечная сила на опоре;
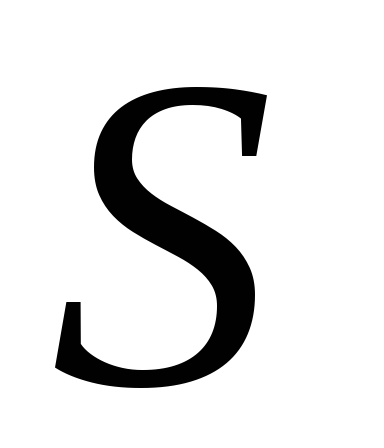 и
и  — статический момент и момент инерции
сечения;
— статический момент и момент инерции
сечения;
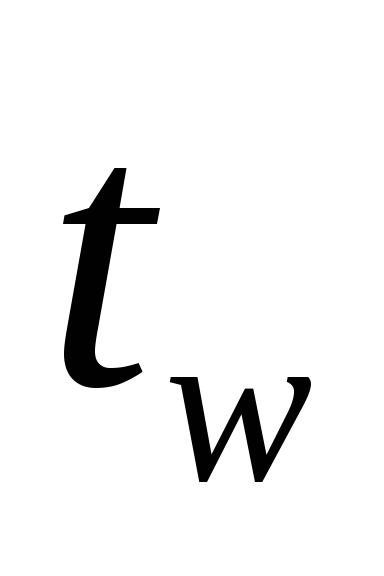 —
толщина стенки балки;
—
толщина стенки балки;
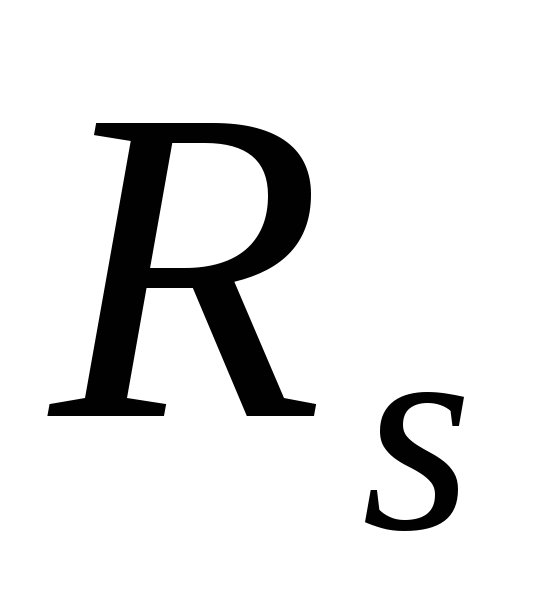 —
расчетное сопротивление стали сдвигу;
определяется по формуле [4]
—
расчетное сопротивление стали сдвигу;
определяется по формуле [4]
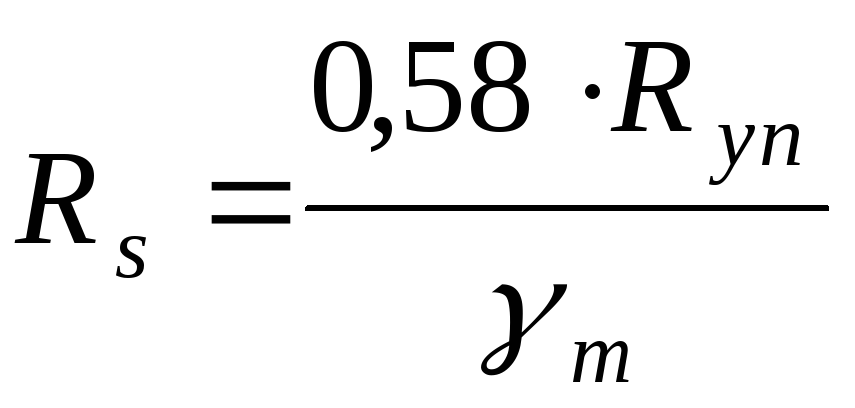 ,
(3.8)
,
(3.8)
где 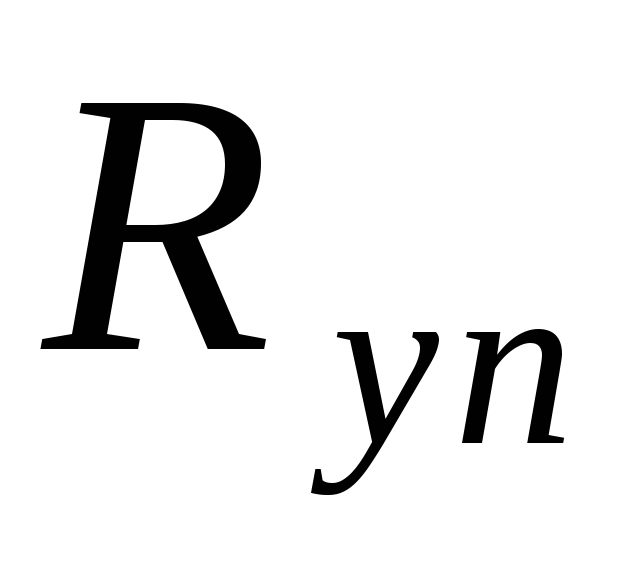 — предел текучести стали, принимаемый
равным значению предела текучести по
государственным стандартам и техническим
условиям на сталь; принимается по таблице
2.6;
— предел текучести стали, принимаемый
равным значению предела текучести по
государственным стандартам и техническим
условиям на сталь; принимается по таблице
2.6;
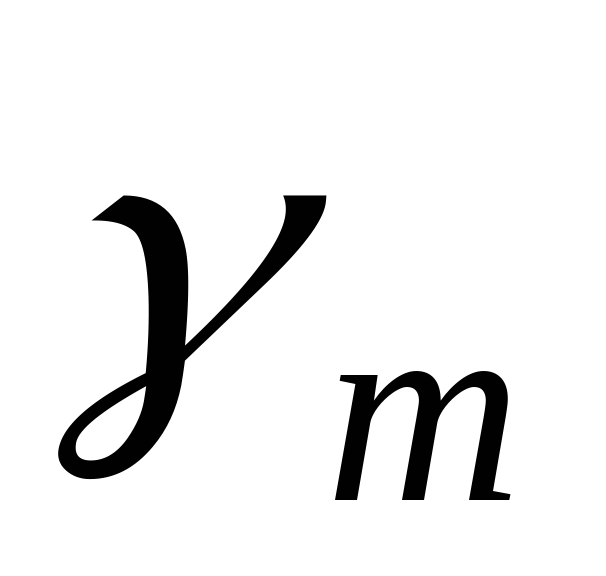 —
коэффициент надежности по материалу
проката [4].
—
коэффициент надежности по материалу
проката [4].
При
сопряжении балок в одном уровне балки
настила прикрепляются к поперечным
ребрам жесткости главных балок болтами,
что несколько ослабляет сечение стенки.
В этом случае значение касательного
напряжения, определенное по формуле
(3.9), следует умножать на коэффициент  ,
вычисляемый по формуле [1]
,
вычисляемый по формуле [1]
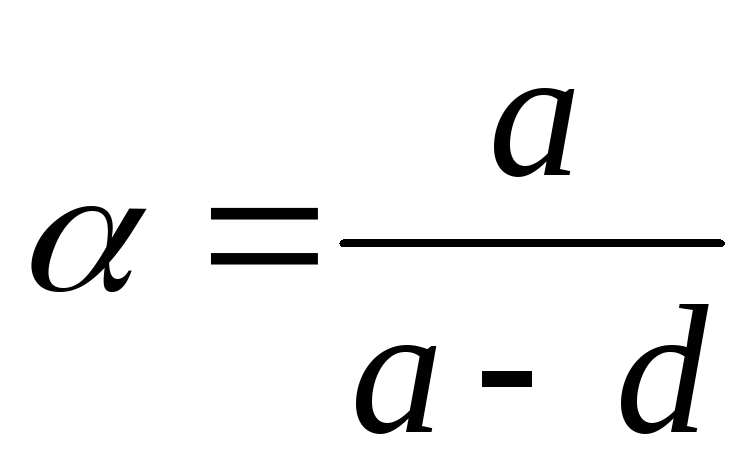 ,
(3.9)
,
(3.9)
где  —
шаг отверстий;
—
шаг отверстий;
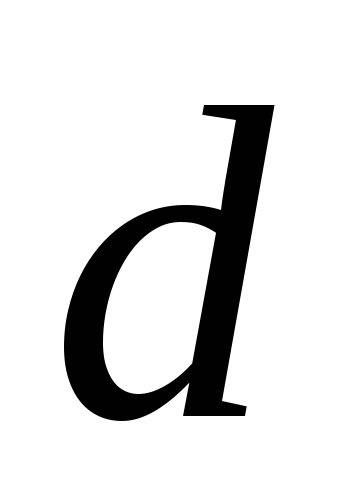 —
диаметр отверстия.
—
диаметр отверстия.
Таблица 3.4 — Значения коэффициента надежности по материалу
Государственный стандарт или технические условия на прокат |
|
ГОСТ27772-88, ТУ 14-1-3023-80 | 1,025 |
ГОСТ27772-88 (стали С590, С590К), ГОСТ380-88** (для круга и квадрата размерами, отсутствующими в ТУ 14-1-3023-80), ГОСТ19281-89, ГОСТ10705-80*, ГОСТ10706-76*, ГОСТ19281-89 [для круга и квадрата с пределом текучести до 380 МПа], ТУ14-1-1308-75 (сталь 14Г2АФ) | 1,05 |
ГОСТ19281-89 [для круга и квадрата с пределом текучести свыше 380 МПа и размерами, отсутствующими в ТУ 14-1-3023-80], ГОСТ8731-87, ТУ 14-3-567-76 | 1,1 |
ГОСТ8731-87, ТУ 14-3-829-79, ТУ 14-3-567-76, ТУ 14-1-1308-75, ТУ 14-1-1772-76 | 1,15 |
Б. Проверка общей устойчивости
Общая устойчивость балки обеспечена настилом, опирающимся на ее сжатый пояс.
В. Проверка местной устойчивости
Местную устойчивость прокатных балок не проверяют, поскольку она обеспечена большими толщинами элементов, что связано с технологией прокатки.
3.3 Проверка жесткости балки
Проверка второго предельного состояния ведется путем определения прогиба балки от действия нормативных нагрузок при допущении упругой работы материала. Для однопролетной балки, нагруженной равномерно распределенной нагрузкой, проверка деформативности производится по формуле [2]
 ,
(3.10)
,
(3.10)
где 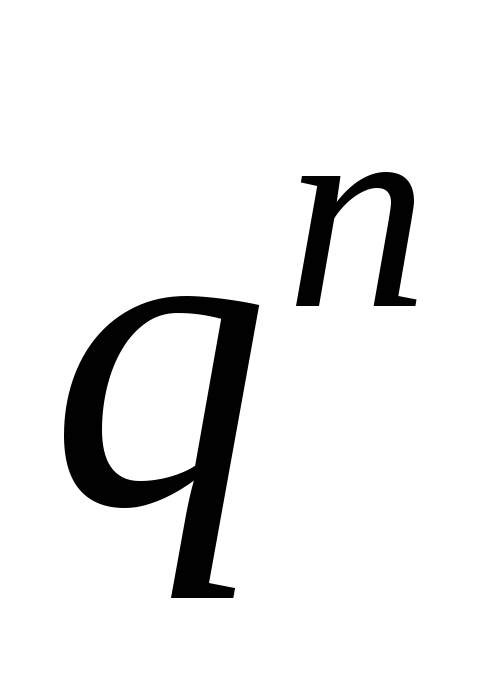 — действительное значение расчетной
погонной нагрузки на балку; определяется
по формуле (3.4) с учетом значений,
соответствующих выбранной балке настила;
— действительное значение расчетной
погонной нагрузки на балку; определяется
по формуле (3.4) с учетом значений,
соответствующих выбранной балке настила;
 —
длина балки настила;
—
длина балки настила;
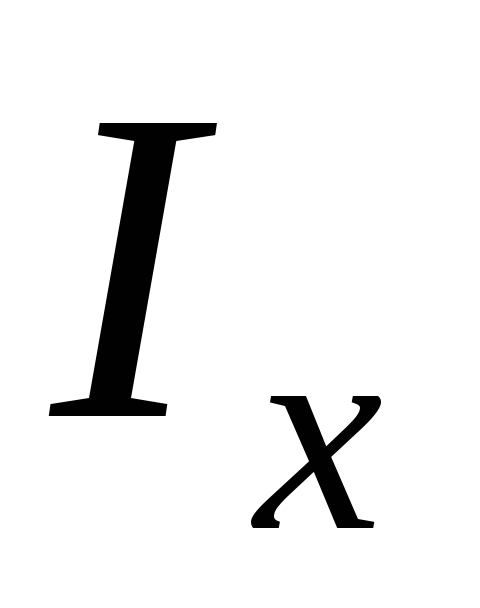 —
табличное значение момента инерции
выбранной балки настила относительно
оси х — х.
—
табличное значение момента инерции
выбранной балки настила относительно
оси х — х.
Полученный относительный прогиб является мерой жесткости балки и не должен превышать нормативного, зависящего от назначения балки [4], т.е.
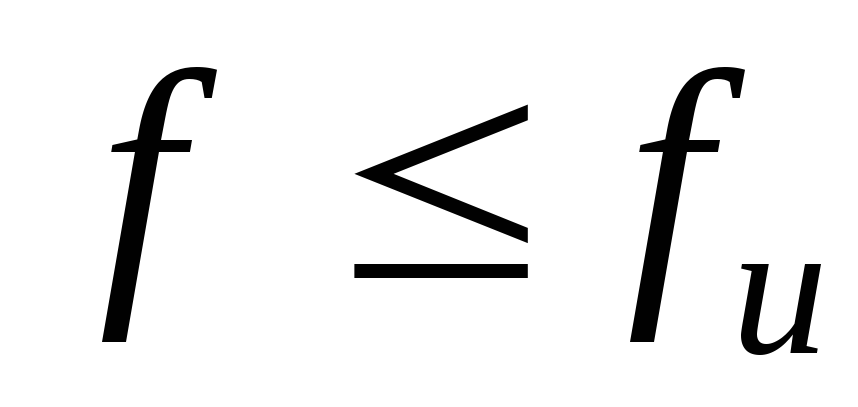 ,
(3.11)
,
(3.11)
где 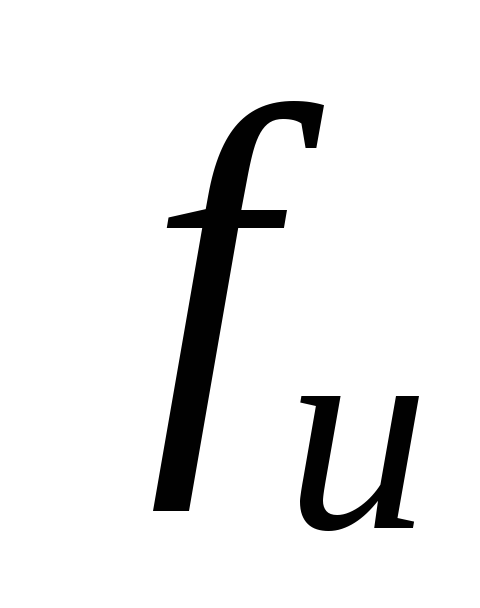 — предельный прогиб, устанавливаемый
нормами; для балок настила [4],
— предельный прогиб, устанавливаемый
нормами; для балок настила [4],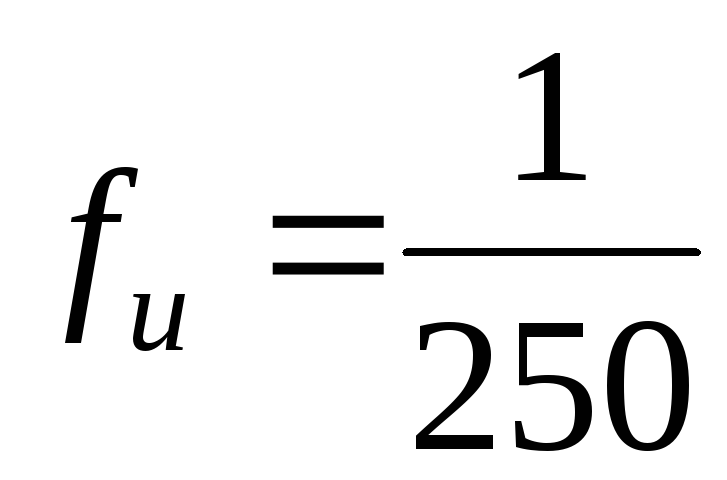 .
.
Если проверка по формуле (3.11) не удовлетворяется, то следует увеличить сечение балки, взяв менее прочный материал, или допустить недоиспользование прочности балки, что менее выгодно.