Строительная механика
— — 19- —
Брянская Государственная инженерно-технологическая академия
Кафедра сопротивления материалов и строительной механики
Утверждены научно-методическим советом академии.
Протокол № .
от “ ” “ ” 20 г.
М Е Т О Д И Ч Е С К И Е У К А З А Н И Я
к выполнению контрольной работы «Расчет фермы» для студентов заочной формы обучения строительных специальностей.
Брянск 2008
Составитель: доцент, к.т.н. В.М. Захаров
Рецензент: доцент, к.т.н., зав. кафедрой СК БГИТА С.Г. Парфенов
Рекомендованы учебно-методической комиссией строительного факультета
Протокол № от « ” “ ” 20 г.
В В Е Д Е Н И Е
В методических указаниях к выполнению контрольной работы «Расчет фермы» приводятся основные теоретические положения и дается пример расчета простых ферм на действие заданной внешней нагрузки.
1 ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ О РАСЧЁТЕ ФЕРМ НА ПОСТОЯННУЮ НАГРУЗКУ
1.1 Понятие о ферме
Ф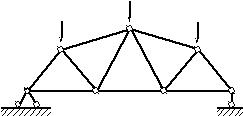 ермой
называется геометрически неизменяемая
система, составленная из прямых стержней,
шарнирно связанных между собой (рисунок
1). Геометрические оси стержней пересекаются
в центре шарнира. Нагрузка прикладывается
в узлах. В стержнях ферм возникают только
продольные силы (изгибающие моменты и
поперечные силы равны нулю).
ермой
называется геометрически неизменяемая
система, составленная из прямых стержней,
шарнирно связанных между собой (рисунок
1). Геометрические оси стержней пересекаются
в центре шарнира. Нагрузка прикладывается
в узлах. В стержнях ферм возникают только
продольные силы (изгибающие моменты и
поперечные силы равны нулю).
Рисунок 1 Ферма
1.2 Определение усилий в стержнях ферм
1.2.1 Способ вырезания узлов
При этом способе последовательно вырезают узлы, содержащие два неизвестных усилия (рисунок 2) и составляют два уравнения равновесия (ΣX = 0 и ΣY= 0) (Рисунок 3).
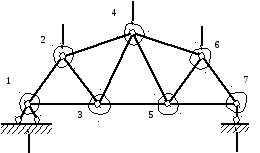
Рисунок 2 Последовательность вырезания узлов
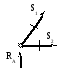
ΣY=0 => определяем S1 ;
ΣX=0 => определяем S2 ;
Рисунок 3 Узел 1
1 .2.2
Способ моментных точек
.2.2
Способ моментных точек

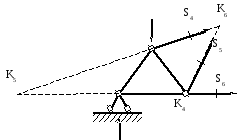
Рисунок 4 Способ моментных точек
При этом способе рассекают ферму на две части так, чтобы при этом перерезанными оказались три её стержня, направления осей которых не пересекаются в одной точке (рисунок 4). Направления осей трёх таких перерезанных стержней пересекаются попарно в трёх точках, не лежащих на одной прямой.
Составляя последовательно уравнения моментов всех сил (внешних и внутренних), действующих на отсечённую часть фермы, относительно этих трёх точек, будем каждый раз получать уравнение с одним неизвестным, представляющим собой усилие в рассечённом стержне, не проходящим через рассматриваемую точку пересечения стержней.
Таким образом, для определения усилия в каком-либо стержне необходимо разрезать ферму так, чтобы в разрез кроме данного стержня попали ещё два других (оси которых не сходятся с ним в общей точке), после чего из уравнения моментов относительно точки пересечения осей этих двух стержней можно легко определить усилие в заданном стержне.
Точка пересечения осей двух стержней, относительно которой составляется уравнение моментов, называется моментной.
1 .2.3
Способ проекций
.2.3
Способ проекций
Рисунок 5 Способ проекций
При этом способе рассекают ферму на две части так, как и в способе моментных точек, но если два стержня из трёх рассеченных параллельны друг другу (рисунок 5). Рассматривают равновесие отсечённой части. Составляя уравнение проекций на ось, перпендикулярную этим двум стержням, определяют усилие в третьем стержне.
ΣY=0 => определяем S5;
2. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ УСИЛИЙ В СТЕРЖНЯХ ФЕРМ
При построении линий влияния усилий в стержне фермы необходимо провести сечение так, чтобы сечение проходило через три стержня, включая интересующий нас.
Так как единичный груз при перемещении проходит через сечение, необходимо рассмотреть два основных случая: груз слева от сечения и груз справа от сечения, а, кроме того, рассмотреть прохождение груза через рассеченную панель. В силу вышесказанного линия влияния усилия в стержне фермы, как правило, состоит из трех прямых: левой – когда груз находится слева от рассеченной панели, правой – когда груз находится справа от рассеченной панели и переходной– когда груз находится над рассеченной панелью (переходит с левой части на правую). В некоторых случаях переходная прямая совпадает с левой (или правой) прямой.
Покажем порядок построения линии влияния
усилия в стержне фермы на примере л.в.
усилия 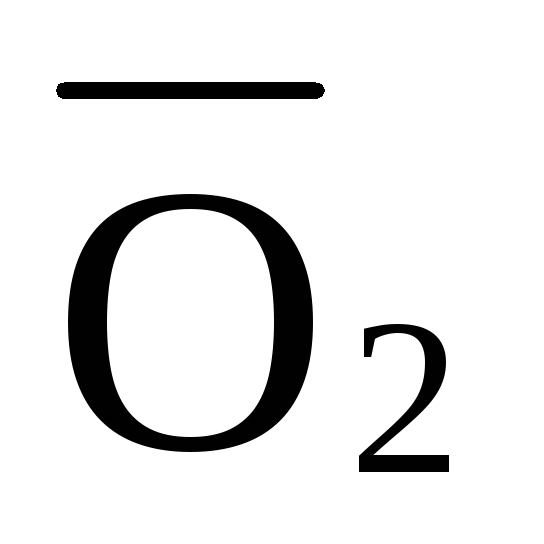 .
Езда поверху.
.
Езда поверху.
Сечение 1-1. Рассеченная
панель – (C-D)
(при езде поверху).Моментная
точка -KO(на пересечении двух оставшихся в сечении
стержней —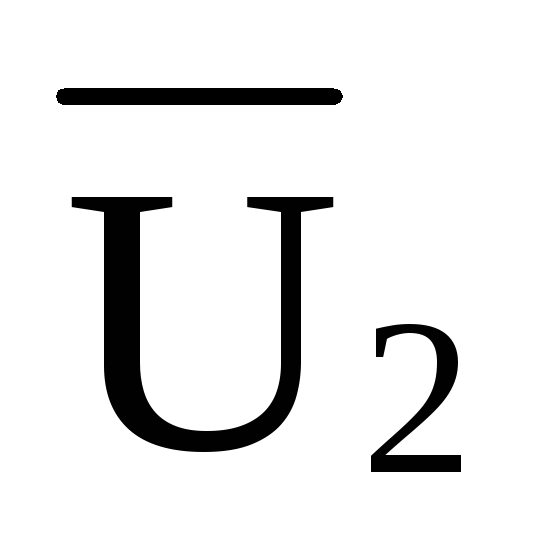
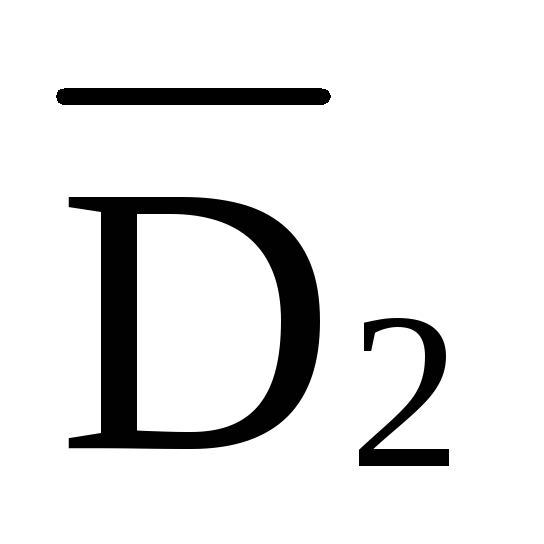 ).
).Рассмотрим два основных случая: груз слева от сечения и груз справа от сечения.
Г руз
слева Груз справа
руз
слева Груз справа
Рассматриваем правую часть Рассматриваем левую часть
Σ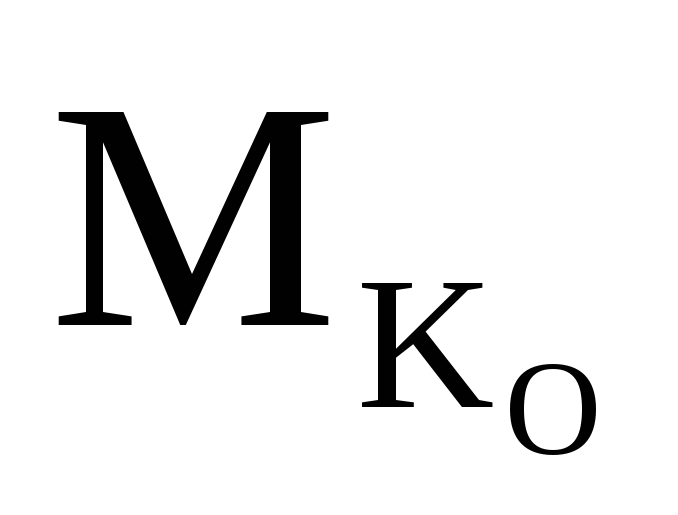 =
0 Σ
=
0 Σ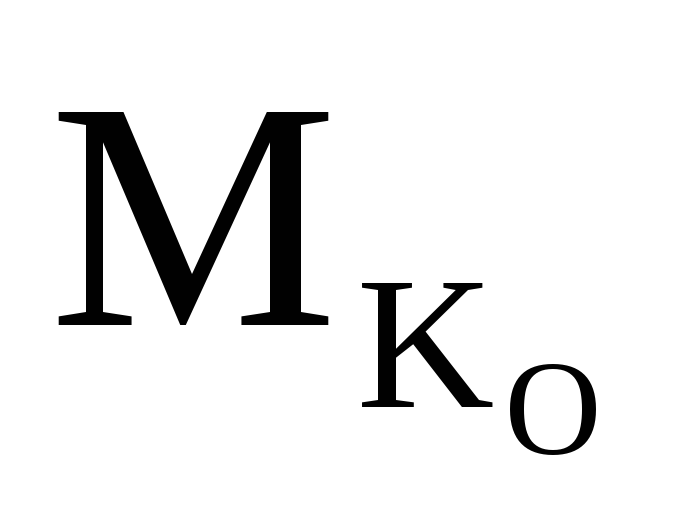 =
0
=
0
— 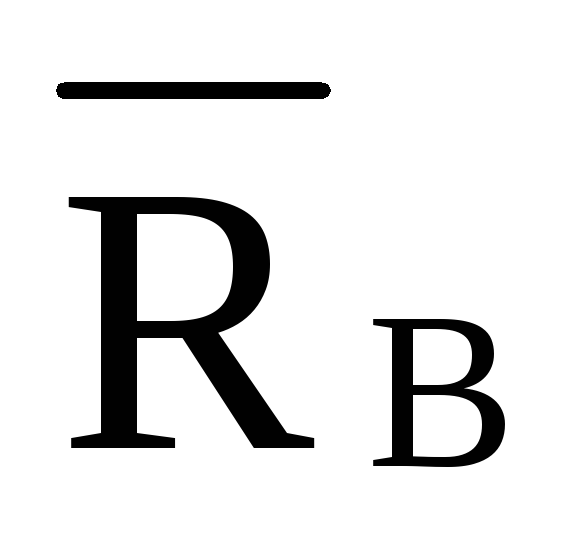
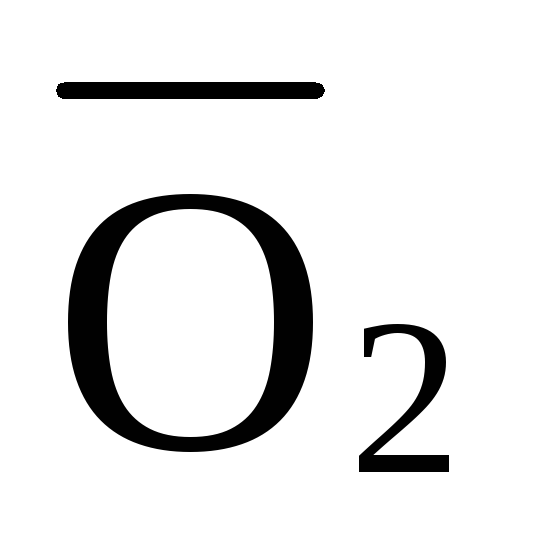 ·
ho =0
·
ho =0 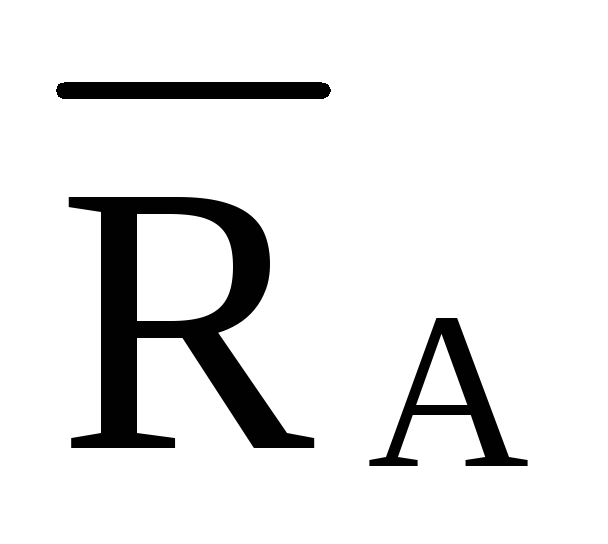 ·
ao +
·
ao + 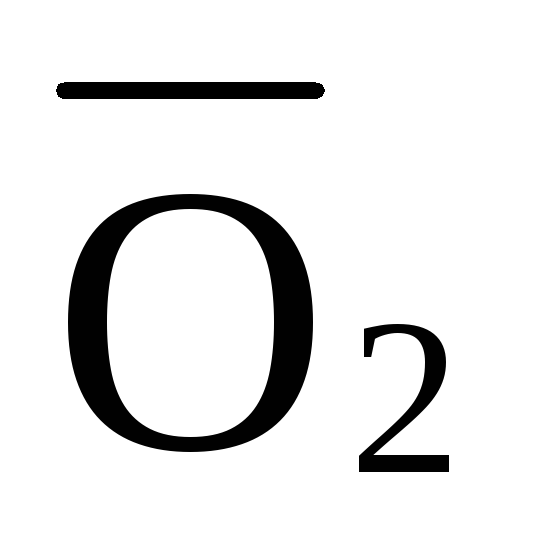 ·
ho =0
·
ho =0 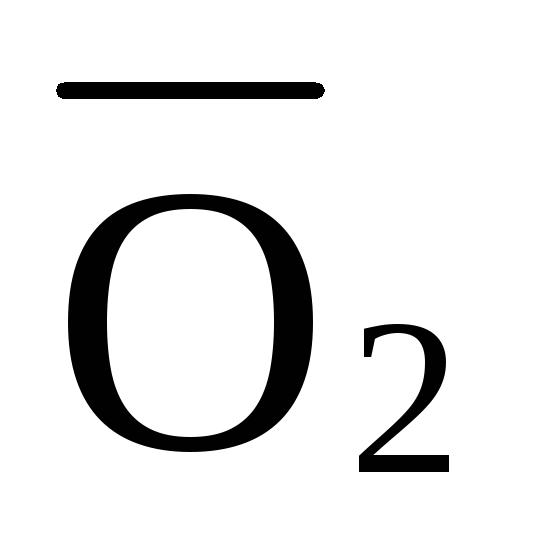 =-
=-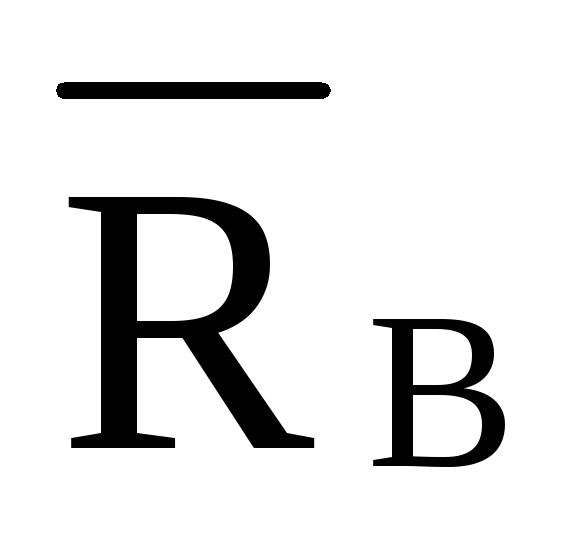 ·
bo /
ho
·
bo /
ho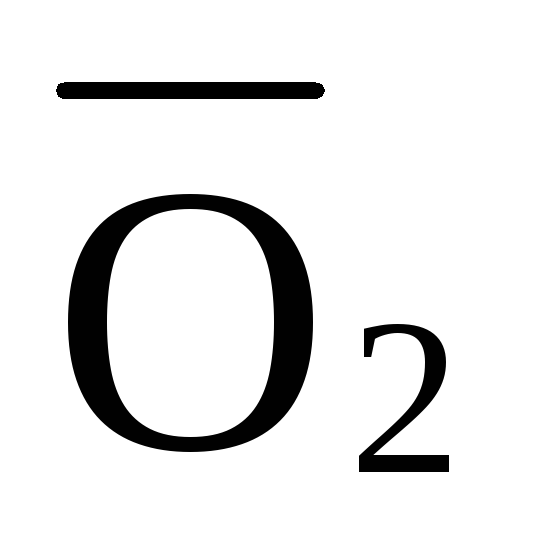
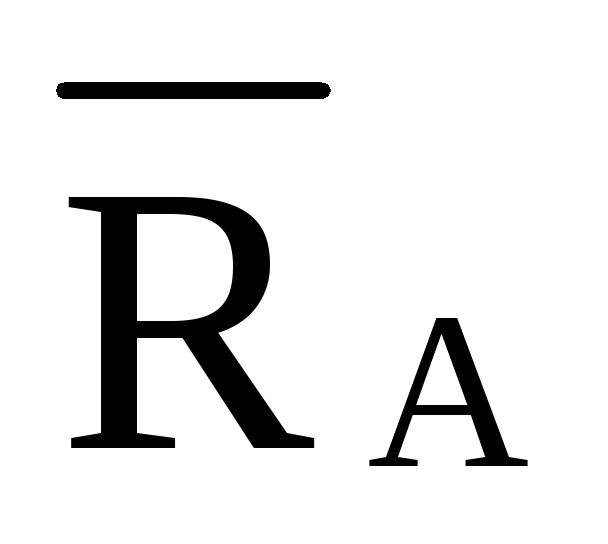 ·
ao /ho
·
ao /ho л.в. 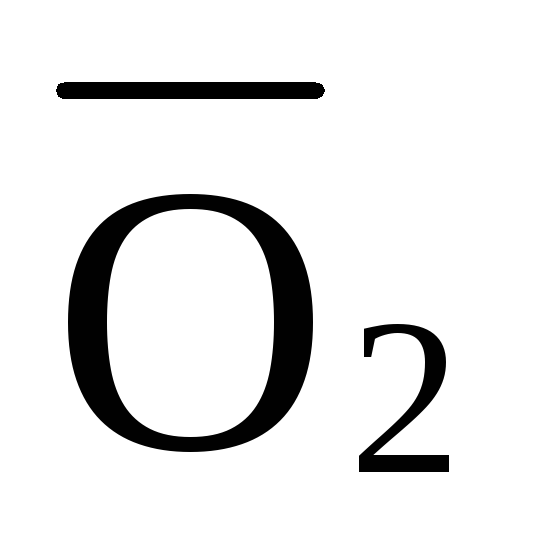 =-(bo / ho)
· л.в.
=-(bo / ho)
· л.в.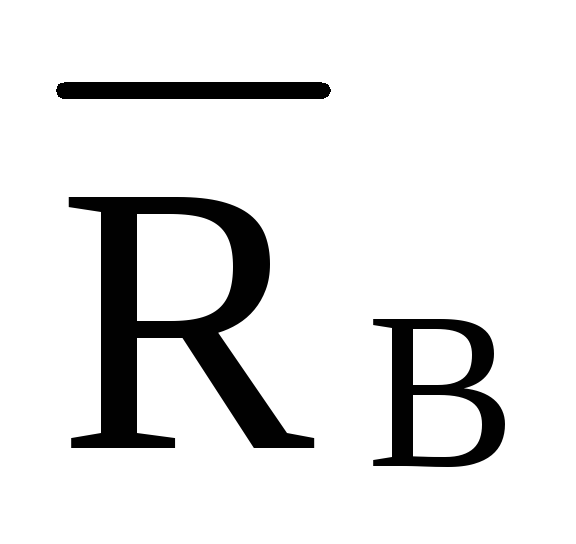 л.в.
л.в. 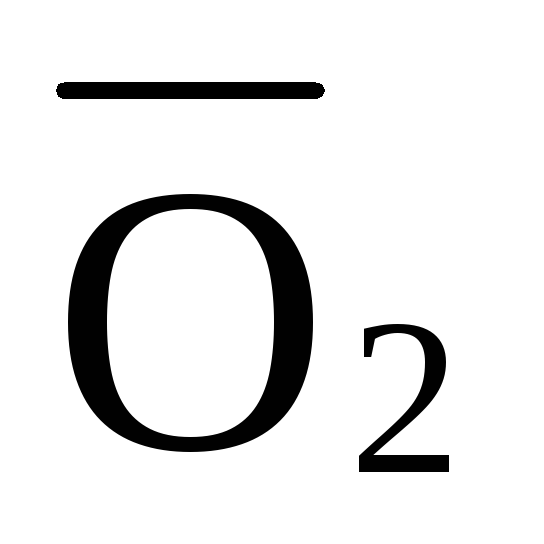 =-
(ao /ho) ·
л.в.
=-
(ao /ho) ·
л.в. 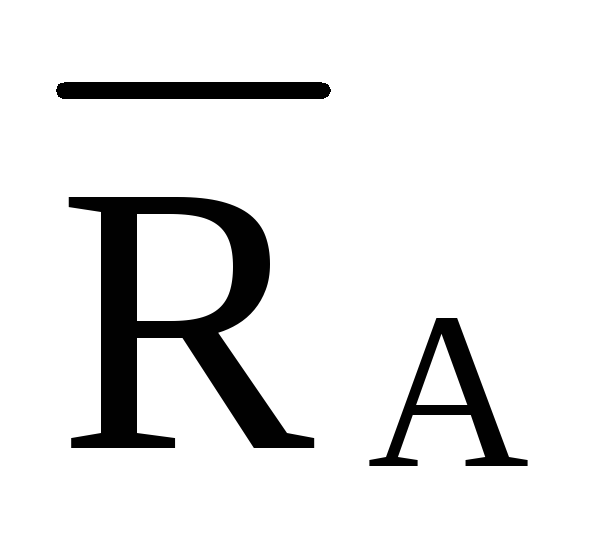
Левая прямая Правая прямая
Слева от рассеченной панели (от узла C) заштриховываем левую прямую. Справа от рассеченной панели (от узлаD) заштриховываем правую прямую.
П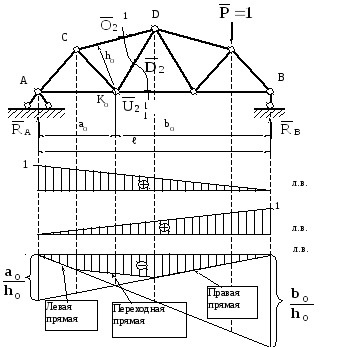 од
рассеченной панелью (между узламиCиD) соединяем ординаты
на левой прямой (под узломC)
и на правой прямой (под узломD)
– получаем переходную прямую
од
рассеченной панелью (между узламиCиD) соединяем ординаты
на левой прямой (под узломC)
и на правой прямой (под узломD)
– получаем переходную прямую
Рисунок 6 Построение л. в. усилий в стержнях фермы
Фермы — Строительная механика
Внутренние усилия в стержнях ферм посредством способа моментной точки определяют по формуле:

где М – момент сил, расположенных на одной из отсеченных частей фермы, относительно моментной точки;
r – плечо усилия N относительно моментной точки.
Из формулы очевидно, что при увеличении r внутреннее усилие N будет снижаться. Достичь увеличения r можно за счет повышения высоты фермы. Из конструктивных особенностей раскосы фермы располагают под углом 45̊ к стойкам и поясам, т.е. увеличение высоты фермы приводит к увеличению длины панелей (поскольку высота фермы с параллельными поясами должна быть равна длине панели) (рис. 1, а). Соответственно это приводит к увеличению массы всей конструкции и экономия материала на стержнях фермы за счет снижения в них, действующих усилий, может оказаться ниже его расхода на сооружение.
Увеличить высоты фермы можно за счет введения в состав каждой панели дополнительных двухопорных ферм – шпренгелей, опирающихся на шарниры основной фермы. Стержни шпренгелей работают лишь на местную нагрузку, т.е. на нагрузку, приложенную в пределах их пролетов. Стержень ab (штриховая линия (рис. 1, б)) необходим лишь для обеспечения геометрической неизменяемости системы и усилие в нем равно нулю. Убрав стержни ab и уменьшив длину вертикальных стержней шпренгелей, получим ферму (рис. 1, в). Перевернув шпренгели получим ферму (рис. 1, г), которая называется шпренгельной. Эта ферма передает местную вертикальную нагрузку, приложенную к верхним дополнительным узлам, вертикально в верхние узлы основной фермы. Такие шпренгели называются одноярусными. Шпренгели также могут местную нагрузку, приложенную к верхним узлам, передавать на нижние узлы (рис. 1, д). Шпренгели, передающие нагрузку, приложенную к дополнительным узлам нижнего пояса, на верхние узлы основной фермы называют двухъярусными.
Подробнее: Шпренгельные фермы
Расчет фермы со шпренгелями от неподвижной нагрузки, построение линий влияния
Ниже приведено решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.

1. Исходные данные
Согласно задания: Неподвижная нагрузка: Постоянная нагрузка – узловая нагрузка F = 40 кН, приложенная к узлам верхнего и нижнего пояса, исключая опорные. Длинна панели d = 3,6 м . Высота t = 2,4 м. Исследуемые стержни – первая и вторая панель слева.
2. Кинематический анализ.
W=2У – Сф – Соп = 2 · 16 – 31 – 3 = 0,
Следовательно, ферма статически определима.
Здесь
У=16 – число узлов фермы, включая опорные;
Сф = 29 – число стержней фермы;
Соп = 3 – число опорных связей.
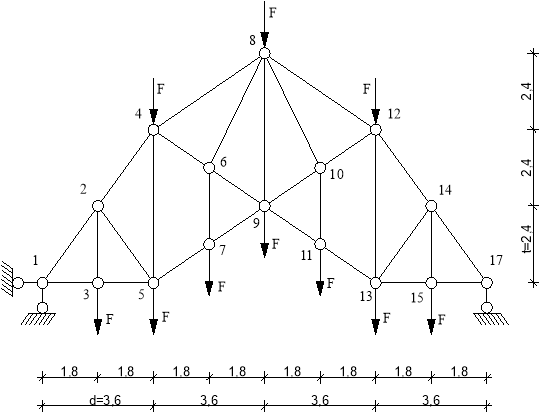
Рис.1
3. Определение опорных реакций от неподвижной нагрузки.
Поскольку ферма симметрична и нагружена симметричной нагрузкой:


Рис.2 Расчетная схема заданной фермы.
4. Определение усилий в стержнях фермы. (аналитически)
Стержни шпренгельной фермы бывают трех категорий
- Стержни принадлежат только основной ферме. Усилия в этих стержнях определяются расчетом только основной фермы.
В нашей ферме – это исследуемые стержни (2-4, 4-5, 5-7, 7-9, 6-9, 8-9).
- Стержни принадлежащие одновременно, как основной ферме, так и дополнительной (шпренгелю). Усилия в этих стержнях определяются как сумма двух усилий. Одно усилие, возникающее в стержне основной фермы, второе – в слившемся с ним шпренгеле.
В нашей ферме – это исследуемые стержни (1-3, 1-2, 3-5, 4-6, 4-8).
3. Стержни принадлежащие только дополнительной ферме (шпренгелю).
Шпренгель рассматриваем как самостоятельную двухопорную ферму.
Усилие в этих стержнях определяется только от нагрузки приложенной
непосредственно к шпренгелю.
В нашей ферме – это исследуемые стержни (2-3, 2-5, 6-7, 6-8).
Разделим ферму на основную и дополнительные (шпренгели).

Рис.3. Основная ферма.

Рис.4. Дополнительные фермы (шпренгели).
Определим усилия в основной ферме.
Предварительно определим функции углов в ферме.
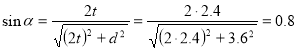
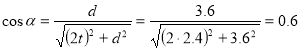
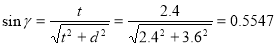
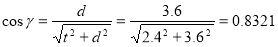
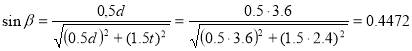
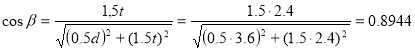
Усилие в стержне (1-4). Усилие находим методом сечений. Рассекаем ферму (сечение I-I)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 5.(рис. 5).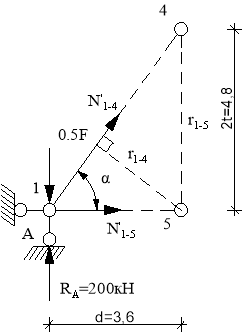
Рис.5
Плечо силы 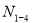 относительно т. 5:
относительно т. 5:
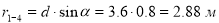
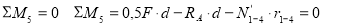
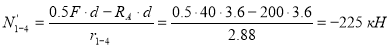
Усилие в стержне 1-5. Усилие находим методом сечений. Рассекаем ферму (сечение I-I)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 4. (рис5).
Плечо силы  относительно т. 4:
относительно т. 4:
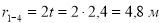
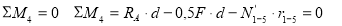
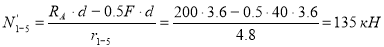
Усилие в стержне 4-5)’. Усилие находим методом сечений. Рассекаем ферму (сечение II-II)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки С.(рис. 6).
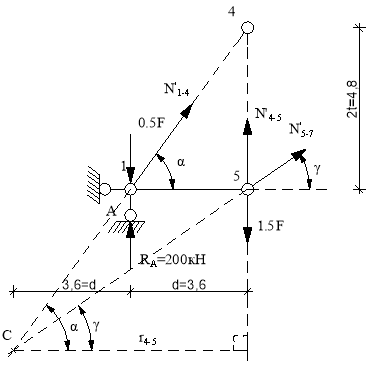
Рис.6
Плечо силы 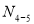 относительно т. С:
относительно т. С:
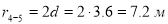
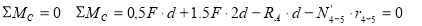

Усилие в стержне 4-9’. Усилие находим методом сечений. Рассекаем ферму (сечение III-III)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно оси У. (рис.7).
Строительная механика — Лекции и примеры решения задач технической механики
Строительная механика это наука о принципах и методах расчета сооружений на прочность, жесткость и устойчивость в условиях действия постоянных и переменных нагрузок.
Её изучение, позволит будущим специалистам стать квалифицированными проектировщиками, создавать экономичные и надежные конструкции, грамотно вести работы по монтажу строительных конструкций.
Строймех является одним из основных базовых предметов для студентов строительных специальностей.
Изучение предмета основано на знании студентами таких общеобразовательных дисциплин, как высшая математика, физика, теоретическая механика и сопротивление материалов.
Целью изучения строимеханики является ознакомление будущих специалистов с теоретическими основами образования и расчёта простых сооружений, понятиями об основах науки о прочности, жёсткости, устойчивости и динамики основных элементов строительных конструкций.
Овладение практическими расчетными приемами строительной механики связано с изучением курсов: «Металлические конструкции», «Железобетонные и каменные конструкции», «Конструкции из дерева и пластмасс». Материал всех указанных дисциплин логически взаимосвязан с материалом данного раздела.
Содержание
- Раздел 1. Кинематический анализ стержневых систем и общие принципы расчета статически определимых систем.
- Основные допущения в строительной механике.
- Расчетная схема сооружения.
- Типы внешних и внутренних связей.
- Кинематический анализ расчетных схем.
- Степень свободы плоской стержневой системы, формулы для ее определения.
- Образование геометрически неизменяемых систем. Мгновенно изменяемые системы и способы проверки систем на мгновенную изменяемость.
- Виды нагрузок и внешних воздействий.
- Типы расчетных схем: балки, консоли, ломаные балки, многопролетные системы, трехшарнирные рамы и арки, фермы и методы их расчета.
- Общие принципы расчета статически определимых систем.
- Определение усилий в статически определимых системах при неподвижной нагрузке.
- Эпюры внутренних усилий в балках
- Определение внутренних усилий в рамах
- Определение внутренних усилий в многопролетной статически определимой балке
- Определение внутренних усилий в трехшарнирных системах
- Основные теоремы об упругих системах.
- Работа внешних и внутренних сил
- Взаимности возможных работ и возможных перемещений
- Общая формула для определения перемещений в плоских стержневых системах
- Техника определения перемещений
- Методика определения перемещений в статически определимых стержневых системах
- Раздел 2. Расчет статически неопределимых систем
- Лекция 5. Расчет статически неопределимых систем методами сил, перемещений, комбинированным, смешанным.
- Лекция 6. Матричный метод расчета перемещений стержневых систем.
- Раздел 3. Расчет пространственных систем
- Лекция 7. Основы и методы расчета пространственных систем.
- Раздел 4. Расчет статически неопределимых систем на ЭВМ
- Лекция 8. Расчет сооружений методом конечных элементов (МКЭ). Расчетные формулы метода перемещений в матричной форме. Идея МКЭ. Матрица жесткости элемента и совокупности элементов. Определение усилий в элементах. Определение напряжений и деформаций в элементах.
- Раздел 5. Расчет стержневых систем методом предельного равновесия
- Лекция 9. Понятие о предельном состоянии. Разрушающие нагрузки. Гипотезы теории предельного равновесия. Расчет статически определимых и неопределимых ферм с учетом пластических свойств материала. Учет пластических свойств материала в балке при чистом и при поперечном изгибе. Пластический момент сопротивления и пластический шарнир. Расчет статически определимых и неопределимых балок с учетом пластических свойств материала. Основные теоремы о разрушающих нагрузках: статическая, кинематическая и о единственности решения. Метод комбинированных механизмов расчета рам.
- Раздел 6. Устойчивость сооружений
- Лекция 8. Основные понятия устойчивости сооружений: виды потери устойчивости, степень свободы, методы решения. Устойчивость систем с конечным числом степеней свободы (статический, энергетический методы). Устойчивость упругих стержней (статический и энергетический методы). Дифференциальное уравнение сжато-изогнутого стержня и его решение методом начальных параметров. Табличные эпюры метода перемещений для сжатых стержней. Учет симметрии при расчете на устойчивость. Деформационный расчет рам.
- Раздел 7. Динамический расчет сооружений
- Лекция 9. Основные понятия динамики сооружений: виды динамических нагрузок, степени свободы, методы решения. Свободные колебания системы с одной степенью свободы с учетом и без учета затухания. Свободные колебания систем с конечным числом степеней свободы. Определение частот и форм свободных колебаний.
Требования к уровню освоения дисциплины
В результате изучения дисциплины студент должен знать:
- Основные методы и практические приемы расчета реальных конструкций по всем предельным расчетным состояниям на различные внешние воздействия;
- Как правильно составить расчетную схему сооружения, выбрать наиболее рациональный метод расчета и как найти истинное распределение напряжений, обеспечив при этом необходимую прочность и жесткость его элементов с учетом реальных свойств строительных материалов и используя современную вычислительную технику.
и уметь:
- Составить расчетную схему к любой задаче строительной механики, выбрать метод расчета и записать требуемые уравнения для ее решения;
- Строить эпюры внутренних усилий (изгибающих моментов, поперечных и продольных сил) в статически определимых и неопределимых системах;
- Определять линейные и угловые перемещения статически определимых и неопределимых систем от внешнего силового воздействия;
- Определять критические нагрузки для рам, балок, ферм, арок, используя точные и приближенные методы расчета;
- Строить эпюры динамических внутренних усилий.
Перечень тем для самостоятельного изучения
- Расчет многопролетной рамы
- Расчет трехшарнирных систем с затяжкой
- Расчет ферм на внеузловую нагрузку
- Расчет составных ферм
- Расчет шпренгельных ферм
- Основы теорий линий влияния и ее применение к расчету простейших статически определимых систем
- Построение линий влияния для различных стержневых систем.
- Расчет статически неопределимых систем методом сил на силовое, температурное воздействия и смещение опор
- Приближенные методы расчета статически неопределимых систем
- Расчет рам, ферм, арок на ЭВМ
Учебно-методическое обеспечение дисциплины
Для уверенного освоения курса рекомендуем использовать следующие источники:
Основная литература
- Александров А.В. Сопротивление материалов / Александров А.В., Потапов В.Д., Державин Б.П. – М.: Высш. шк., 2001. – 560 с.
- Анохин Н.Н. Строительная механика в примерах и задачах. Ч. I. Статически определимые системы: Учеб. Пос. – М.: Изд-во АСВ, 1999.
- Анохин Н.Н. Строительная механика в примерах и задачах. Ч. II. Статически неопределимые системы: Учеб. Пос. – М.: Изд-во АСВ, 2000.
- Киселев В.А. Строительная механика. Общий курс.– М.: Стройиздат, 1986. – 520 с.
- Леонтьев Н.Н., Соболев Д.Н., Амосов А.А. Основы строительной механики стержневых систем. — М.: АСВ, 1996.
- Роте А. Статика стержневых систем / Пер. с нем. О.О. Андреева; Под ред. Р.Р. Матевосяна. – М.: Стройиздат, 1988. – 512 с.
- Саргсян А.Е. Строительная механика. Механика инженерных конструкций/Саргсян А.Е. – М.: Высш. шк., 2004. – 462 с.
- Степин П.А. Сопротивление материалов / Степин В.А.– М.: Высш. шк., 1983.–303 с.
Дополнительная литература
- Вагапов Р.Ф., Капитонов С.М. Строительная механика. Конспект лекций, часть 1, Уфа, Издательство УГНТУ, 1996.- 192с.
- Вагапов Р.Ф., Капитонов С.М. Строительная механика. Конспект лекций, часть 2, Уфа, Издательство УГНТУ, 1998.- 146с.
- Статический расчёт плоских стержневых систем методом конечных элементов на ПЭВМ IBM PC. Уфа, Уфимский нефтяной институт, 1990.- 14с.
- Кроткова Л.В., Филипович А.И., Архипов В.Г., Луцык Е.В. Сборник задач по строительной механике. Учебное пособие. – М.: изд-во АСВ, 2008. – 224 с.
- Кроткова Л.В. Сборник задач по строительной механике. Учебное пособие. – М.: изд-во АСВ, 1994 . – 216 стр.
- Кроткова Л.В. Учебное пособие к практическим занятиям по строительной механике. – М.: изд-во АСВ, 1998 . – 178 стр.
Электронные средства обеспечения
- Программа SAPS / Статический расчет плоских стержневых систем МКЭ;
- Вычислительный комплекс SCAD для расчета конструкций методом конечных элементов;
- Научно-исследовательский вычислительный комплекс ANSYS.
Вы здесь:
Техническая механика > Строительная механикаСТРОИТЕЛЬНАЯ МЕХАНИКА. Учебное издание.
Предисловие …. 3Введение …. 7
Глава 1. Кинематический анализ сооружений …. 14
§ 1.1. Опоры …. 14
§ 1.2. Условия геометрической неизменяемости стержневых систем …. 16
§ 1.3. Условия статической определимости геометрически неизменяемых стержневых систем …. 23
Глава 2. Балки …. 27
§ 2.1. Общие сведения …. 27
§ 2.2. Линии влияния опорных реакций для однопролетных и консольных балок …. 31
§ 2.3. Линии влияния изгибающих моментов и поперечных сил для однопролетных и консольных балок …. 34
§ 2.4. Линии влияния при узловой передаче нагрузки …. 38
§ 2.5. Определение усилий с помощью линий влияния …. 41
§ 2.6. Определение невыгоднейшего положения нагрузки на сооружении. Эквивалентная нагрузка …. 45
§ 2.7. Многопролетные статически определимые балки …. 51
§ 2.8. Определение усилий в многопролетных статически определимых балках от неподвижной нагрузки …. 55
§ 2.9. Линии влияния усилий для многопролетных статически определимых балок …. 59
§ 2.10. Определение усилий в статически определимых балках с ломаными осями от неподвижной нагрузки …. 62
§ 2.11. Построение линий влияния в балках кинематическим методом …. 64
Глава 3. Трехшарнирные арки и рамы …. 70
§ 3.1. Понятие об арке и сравнение ее с балкой …. 70
§ 3.2. Аналитический расчет трехшарнирной арки …. 73
§ 3.3. Графический расчет трехшарнирной арки. Многоугольник давления …. 82
§ 3.4. Уравнение рациональной оси трехшарнирной арки …. 87
§ 3.5. Расчет трехшарнирных арок на подвижную нагрузку …. 88
§ 3.6. Ядровые моменты и нормальные напряжения …. 95
Глава 4. Плоские фермы …. 98
§ 4.1. Понятие о ферме. Классификация ферм …. 98
§ 4.2. Определение усилий в стержнях простейших ферм …. 101
§ 4.3. Определение усилий в стержнях сложных ферм …. 118
§ 4.4. Распределение усилий в элементах ферм различного очертания …. 121
§ 4.5. Исследование неизменяемости ферм …. 125
§ 4.6. Линии влияния усилий в стержнях простейших ферм …. 133
§ 4.7. Линии влияния усилий в стержнях сложных ферм …. 142
§ 4.8. Шпренгельные системы …. 146
§ 4.9. Трехшарнирные арочные фермы и комбинированные системы …. 152
Глава 5. Определение перемещений в упругих системах …. 159
§ 5.1. Работа виешних сил. Потенциальная энергия …. 159
§ 5.2. Теорема о взаимности работ …. 163
§ 5.3. Теорема о взаимности перемещений …. 166
§ 5.4. Определение перемещений. Интеграл Мора …. 168
§ 5.5. Правило Верещагина …. 173
§ 5.6. Примеры расчета …. 179
§ 5.7. Температурные перемещения …. 185
§ 5.8. Эиергетический прием определения перемещений …. 188
§ 5.9. Перемещения статически определимых систем, вызываемые перемещениями опор …. 189
Глава 6. Расчет статически неопределимых систем методом сил …. 193
§ 6.1. Статическая неопределимость …. 193
§ 6.2. Канонические у равнени я метода сил …. 199
§ 6.3. Расчет статически неопределимых систем на действие заданной нагрузки …. 202
§ 6.4. Расчет статически неопределимых систем на действие температуры …. 213
§ 6.5. Сопоставление канонических уравнений при расчете систем на перемещения опор …. 215
§ 6.6. Определениеперемещенийвстатическинеопределимыхсистемах …. 219
§ 6.7. Построение эпюр поперечных и продольных сил. Проверка эпюр …. 222
§ 6.8. Способ упругого центра …. 228
§ 6.9. Линии влияния простейших статически неопределимых систем …. 231
§ 6.10. Использование симметрии …. 238
§ 6.11. Группировка неизвестных …. 241
§ 6.12. Симметричные и обратносимметричные нагрузки …. 243
§ 6.13. Способ преобразования нагрузки …. 245
§ 6.14. Проверка коэффициентов и свободных членов системы канонических уравнений …. 247
§ 6.15. Примеры расчета рам …. 249
§ 6.16. «Модели» линий влияния усилий для неразрезных балок …. 263
Глава 7. Расчет статически неопределимых систем методами перемещений и смешанным …. 265
§ 7.1. Выбор неизвестных в методе перемещений …. 265
§ 7.2. Определение числа неизвестных …. 266
§ 7.3. Основная система …. 269
§ 7.4. Канонические уравнения …. 276
§ 7.5. Статический способ определения коэффициентов и свободных членов системы канонических уравнений …. 280
§ 7.6. Определение коэффициентов и свободиых членов системы канонических уравнений перемножением эпюр …. 283
§ 7.7. Проверка коэффициентов и свободных членов системы канонических уравнений метода перемещений …. 286
§ 7.8. Построение эпюр M, Q и N в заданной системе …. 287
§ 7.9. Расчет методом перемещений на действие темцературы …. 288
§ 7.10. Использование симметрии при расчете рам методом перемещений …. 292
§ 7.11. Пример расчета рамы методом перемещений …. 295
§ 7.12. Смешанный метод расчета …. 302
§ 7.13. Комбинированное решение задач методами сил и перемещений …. 307
§ 7.14. Построение линий влияния методом перемещений …. 309
Глава 8. Полная система уравненнй строительной механики стержиевых систем и методы ее решения …. 313
§ 8.1. Общие замечания …. 313
§ 8.2. Составление уравнений равновесия, статические уравнения. Исследование образования систем …. 313
§ 8.3. Составление уравнений совместности, геометрические уравнения. Принцип двойственности …. 321
§ 8.4. Закон Гука. Физические уравнения …. 326
§ 8.5. Система уравнений строительной механики. Смешанный метод …. 328
§ 8.6. Метод перемещений …. 333
§ 8.7. Метод сил …. 341
§ 8.8. Уравнения теории упругости и их связь с уравнениями строительной механики …. 345
Глава 9. Расчет стержневых систем с использованием ЭВМ …. 352
§ 9.1. Вводные замечания …. 352
§ 9.2. Полуавтоматизированный расчет статически неопределимых систем с использованием калькуляторов …. 353
§ 9.3. Автоматизация расчета стержневых систем. Полная система уравнений строительной механики для стержня …. 363
§ 9.4. Матрицы реакций (жесткости) для плоских и пространственных стержней и их использование …. 372
§ 9.5. Описание учебного комплекса по расчету стержневых систем. Внутреннее и внешнее представление исходных данных. Блок-схема комплекса по расчету стержневых систем …. 389
Глава 10. Учет геометрической и физической нелинейности при расчете стержневых систем …. 397
§ 10.1. 0бщие замечания …. 397
§ 10.2. Расчет стержневых систем с учетом геометрической нелинейности …. 398
§ 10.3. Устойчивость стержневых систем …. 411
§ 10.4. Расчет стержневых систем с учетом физической нелинейности. Предельное состоянне …. 419
Глава 11. Метод конечных элементов (МКЭ) …. 435
§ 11.1. Общие замечания …. 435
§ 11.2. Связь МКЭ с уравнениями строительной механики …. 435
§ 11.3. Построение магрнц жесткости для решения плоской задачи теории упругости …. 456
§ 11.4. Предельный переход для плоской задачи …. 464
§ 11.5. Построение матриц жесткости для решения объемной задачи теории упругости …. 467
§ 11.6. Сложные элементы, построение матриц жесткости для элементов с искривленной границей …. 471
§ 11.7. Построение матриц реакций для расчета пластинок и оболочек …. 485
§ 11.8. Особенности комплексов для расчета конструкций по МКЭ. Суперэлементный подход …. 493
Глава 12. Основы динамики сооружений …. 501
§ 12.1. Виды динамических воздействий. Понятие о степенях свободы …. 501
§ 12.2. Свободные колебания систем с одной степенью свободы ….
§ 12.3. Расчет систем с одной степенью свободы при действии периодической нагрузки …. 518
§ 12.4. Расчет систем с одной степенью свободы при действии произвольной нагрузки. Интеграл Дюамеля …. 524
§ 12.5. Движение системы с двумя степенями свободы. Приведение в системы с двумя степенями свободы к двум системам с одной степенью свободы …. 529
§ 12.6. Кинетическая энергия. Уравнение Лагранжа …. 536
§ 12.7. Приведение кинематического воздействия к силовому …. 544
§ 12.8. Сведение системы дифференциальных уравнений динамики к разделяющимся у равнениям с помощью решения проблемы собственных значений …. 546
§ 12.9. Метод постоянного ускорения и его использование для решения динамических задач …. 550
Глава 13. Сведения из вычислительной математики, используемые в строительной механике …. 554
§ 13.1. Общие замечания …. 554
§ 13.2. Матрицы, их виды, простейшие операции над матрицами …. 555
§ 13.3. Перемножение матриц. Обратная матрица …. 557
§ 13.4. Метод Гаусса для решения систем линейных уравнений. Разложение матрицы в произведение трех матриц …. 562
§ 13.5. Исследование систем линейных уравнений. Однородные уравнения. Решение n уравнений с m неизвестными с использованием метода Гаусса …. 574
§ 13.6. Квадратичная форма. Матрица квадратичной формы. Производная от квадратичной формы …. 578
§ 13.7. Собственные числа и собственныеве векторы положительно определенной матрицы …. 581
§ 13.8. Однородные координаты и интегрирование по треугольной области …. 594
§ 13.9. Соотношения между тригонометрическими, гиперболическими функциями и экспоненциальной функцией …. 599
Заключение …. 600
Литература …. 601
Предметный указатель …. 602
Расчёт и конструирование плоской фермы | Металлоконструкции
Белорусско-Российский университет
Кафедра «Транспортные технологические машины»
Курсовая работа по дисциплине « Строительная механика и металлические конструкции»
Тема: «Расчёт и конструирование плоской фермы»
Могилёв 2018
Исходные данные:
длинна фермы — L=16 м;
постоянная нагрузка — F=100 кН;
подвижная нагрузка — q=10 кН;
высота фермы — h=6 м;
панель 3 слева.
Содержание
Введение………………………………………………………………….3
1 Выбор геометрических параметров фермы………………………….4
2 Исследование фермы на геометрическую неизменяемость…………4
3 Аналитическое определение усилий в стержнях заданной панели…5
4 Построение линий влияния стержней заданной панели….…………8
5 Определение расчетных усилий в стержнях заданной панели от действия постоянной нагрузки и системы, связанных между собой подвижных сил…………………………………………………………………14
6 Подбор сечений стержней фермы……………………………………15
7 Расчет числа заклепок………………………………………………..19
8 Расчет длины сварных швов…………………………………………20
9 Построение грузовой диаграммы Максвелла – Кремоны при невыгодном загружении фермы подвижной нагрузкой, а также единичных диаграмм……………………………………………………………………….21
10 Определение прогибов узлов ездового пояса фермы при невыгодном положении подвижной нагрузки и построение линии прогибов……………………………………………………………………….23
Заключение……………………………………………………………..24
Список используемых источников……………………………………25
Состав: Построение линий влияния и диаграммы Макссвелла-Кремоны — формат А1, Панель (СБ), ПЗ 
Софт: КОМПАС-3D v17
Определение усилий в стержнях фермы
Фермы, в которых новые узлы добавляются посредством двух стержней, не лежащих на одной линии (из шарнирного треугольника), называются простейшими.
Реакции в опорах фермы определяются как для простой однопролетной балки с помощью уравнений равновесия.
Внутренние усилия в стержнях фермы при расчете принимаются положительными (направленными от узлов). Если после выполнения расчета усилие в стержне будет отрицательным, то для него меняют направление.
При решении задач примем следующие условные обозначения: внутренние усилия в стержнях верхнего пояса фермы обозначим буквой О, в стержнях нижнего пояса – U, в раскосах – D, в стойках – V. В качестве индексов у этих обозначений применяются цифры, обозначающие узлы фермы, расположенные на концах рассматриваемого стержня.
Для расчета простых ферм применяются следующие методы:
1) метод моментной точки;
2) метод проекций;
3) метод вырезания узлов.
Метод моментных точек
Способ моментной точки применяется, когда можно разрезать ферму на две части. Сечение должно рассечь не более трех стержней, один из которых и является стержнем, в котором требуется найти внутреннее усилие. При этом два стержня, внутренние усилия в которых не требуется знать, должны соединяться в одной точке, называемой моментной.
После того как ферма разрезана на две части, более простую часть (с точки зрения дальнейшего расчета) оставляют, а остальное откидывают. Составляется уравнение моментов относительно моментной точки, из которого и определяют требуемое усилие.
Случаи применения способа моментной точки:
1. Сечение разрезает кроме стержня, усилие в котором требуется определить, любое число стержней, пересекающихся в одной точке, не лежащей на линии рассматриваемого стержня.
2. Когда сечение пересекает более трех стержней, не пересекающихся в одной точке, если усилия во всех стержнях, кроме трех, уже найдены.
3. Когда можно провести разрез, пересекающий любое число стрежней сверх трех, если при этом каждый добавочный стержень пересекается дважды.
Преимуществом данного метода является то, что ошибка при расчете усилия в одном стержне не влияет на расчет усилий в остальных стержнях.
Метод проекций
Данный метод применяется, когда два из трех разрезанных стержней, усилия в которых определять не требуется, параллельны друг другу.
Метод вырезания узлов
В методе вырезания узлов вначале вырезается узел, в котором пересекаются не более двух стержней с неизвестными усилиями, и далее последовательно вырезая узлы достигают требуемого стержня. При этом в каждом из вырезаемых узлов должно пересекаться не более двух неизвестных стержней с неизвестными усилиями.
Недостатком метода вырезания узлов является то, что ошибка, допущенная при расчете одного узла, влияет на результат дальнейших расчетов.
Кроме простейших ферм существуют системы с более сложной геометрической структурой, называемые сложными.
Для их решения применяется метод замены стержней.
Путем замены стержней ферма превращается в простую, которая кладется в основу расчета. Система, полученная в результате такого преобразования, называется заменяющей.
Алгоритм определения положения заменяющего стержня:
1) Убрать какой-либо стержень;
2) Последовательно убирать узлы фермы, присоединенные двумя стержнями каждый, такое отбрасывание не оказывает влияние на неизменяемость оставшейся части;
3) Отбрасывание узлов продолжается до тех пор, пока не обнаружится стержень, не имеющий достаточной связи с остающейся частью системы. Стержень необходимый для его закрепления и будет заменяющий.
4) Если полученная ферма не будет принадлежать к простейшим, то из нее следует устранить еще один стержень и повторить предыдущие действия.
Примеры с решениями.
