Калькулятор балки: Расчет балки на прогиб и прочность

20.10.1972 By alexxlab Разное Комментариев нет

Содержание

Онлайн калькулятор: Опорные реакции простой балки

Данный онлайн калькулятор предназначен для нахождения опорных реакций в простейшей балке, находящейся под воздействием поперечных сил. Простая балка — прямолинейный брус, закрепленная на двух опорах: одной — шарнирно-неподвижной (опора А), другой — шарнирно-подвижной (опора В). Калькулятор выводит опорные реакции V_A и V_B, уравнения равновесия в символьном виде и показывает модель нагрузок. Обратите внимание, что если требуется задать нагрузку действующую левее опоры A, то расстояние от опоры нужно задать со знаком минус. Теорию и формулы расчета можно найти ниже под калькулятором.

Опорные реакции простой балки

Расстояние между опорами, м

Нагрузка

	Расстояние от опоры A	Нагрузка	Значение	Направление	Направление момента	Протяженность	Изменение

Записей:

51020501001000

Нагрузка

Расстояние от опоры A

Отрицательное, если нагрузка приложена к точке, лежащей левее опоры.

НагрузкаСосредоточенная нагрузка, кНРавномерно распределенная, кН/мЛинейно распределенная, кН/мМомент, кН*М

Значение

Направление↓ вниз↑ вверх

Направление момента↻ По часовой стрелке↺ Против часовой стрелки

Протяженность

Изменение\ Убывание/ Возрастание

Импортировать данныеОшибка импорта

Данные

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;L;50.5;up;anticlockwise;50.5;increase

Загрузить данные из csv файла

Детали

Точность вычисления

Знаков после запятой: 2

Реакция опоры А, кН

Реакция опоры B, кН

Положительное направление момента сил

↻ По часовой стрелке

↺ Против часовой стрелки

Уравнения моментов сил

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Реакции опор

Под воздействием нагрузок в опорах балки возникают уравновешивающие силы, называемые реакциями опор. Эти силы зависят от вида нагрузки и типа самих опор.

Шарнирно подвижная опора

Шарнирно подвижная опора ( в нашей модели обозначена как «B») позволяет балке свободно перемещаться в горизонтальной плоскости и препятствует вертикальному перемещению, поэтому при любой нагрузке она имеет только вертикальную реакцию V_B.

Шарнирно неподвижная опора

Шарнирно неподвижная опора крепится к балке, что препятствует её горизонтальному и вертикальному перемещению. При наличии сил, действующих на балку в горизонтальной плоскости, эта опора дает еще и горизонтальную реакцию. Однако в нашей модели все силы действуют поперечно балке, поэтому горизонтальная реакция опоры A всегда будет равна нулю.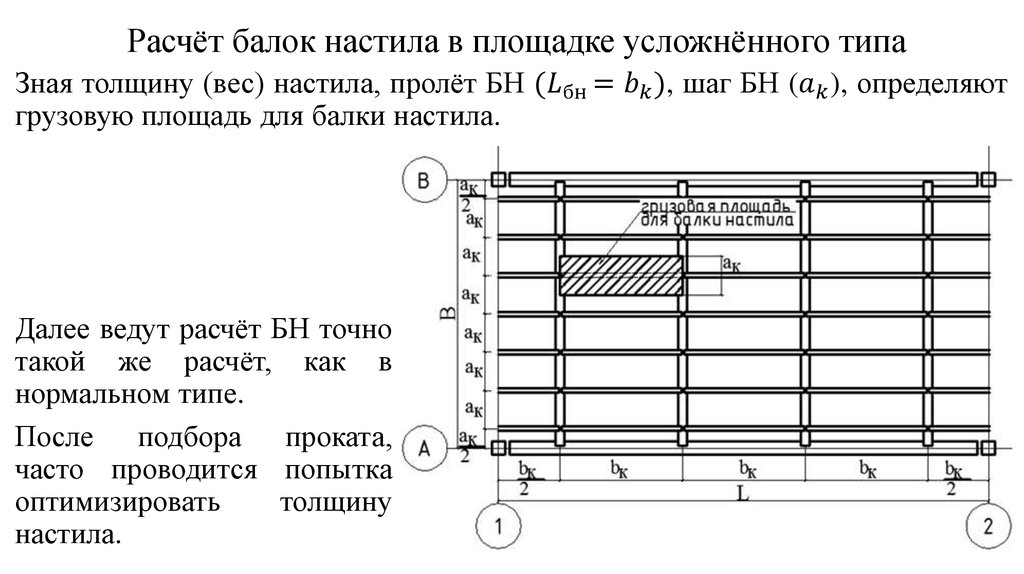 Вертикальную реакцию опоры A обозначим V_A.

Уравнения равновесия

Как мы знаем из статики, все силы и моменты сил в неподвижной системе, уравновешены. Поэтому суммы сил и моментов в любой точке этой системы равны нулю.

Все силы при поперечной нагрузке на простую балку действуют параллельно оси Y, поэтому можно составить только два независимых уравнения равновесия для проекции сил и моментов на ось Y. Этого вполне достаточно для нахождения двух неизвестных реакций опор V_A и V_B.
При составлении уравнений у нас есть выбор:

составить одно уравнение равновесия проекции сил и одно уравнение равновесия моментов в некоторой точке
составить два уравнения равновесия моментов в двух точках.

Воспользуемся вторым способом, а первый оставим для проверки полученного результата.
Удобнее всего составлять уравнения для точек А и B, в которых находятся опоры:

Напомним, что моментом силы в определенной точке называется произведение силы F на кратчайшее расстояние от этой точки до линии действия силы (плечо) l:

Исходя из этого, уравнения равновесия моментов в точках А и B для системы поперечных сил F₁. ..F_n, действующих на балку приобретают вид:

Где F_i — модуль приложенной силы или реакции опоры в Ньютонах. l_{i_A} и l_{i_B} — длина рычага в метрах (кратчайшее расстояние от точки приложения силы i до опоры A и B соответственно). s

i_A и s_{i_B} — знак момента силы i в точке A и B соответственно.
Правило выбора знаков момента сил: знак положительный (+1) для момента, закручивающего балку вокруг выбранной точки по часовой стрелке ↻ и отрицательный (-1) для противоположного направления ↺. Можно выбрать и противоположные значения. Уравнения примут немного другой вид, но результат от этого не изменится.

Система сосредоточенных сил, действующих на простую балку

Например, для системы сил, показанной на рисунке выше, уравнения равновесия можно записать следующим образом:

Вычисляя, получаем значения реакций опор: V

A = 15.42 и V_B = 14.58. Проверим, что сумма всех сил равна нулю (для сил действующих вниз — знак положительный, для действующих вверх — отрицательный):

Составляя уравнения, мы исходили из того, что реакции обеих опор направлены вверх.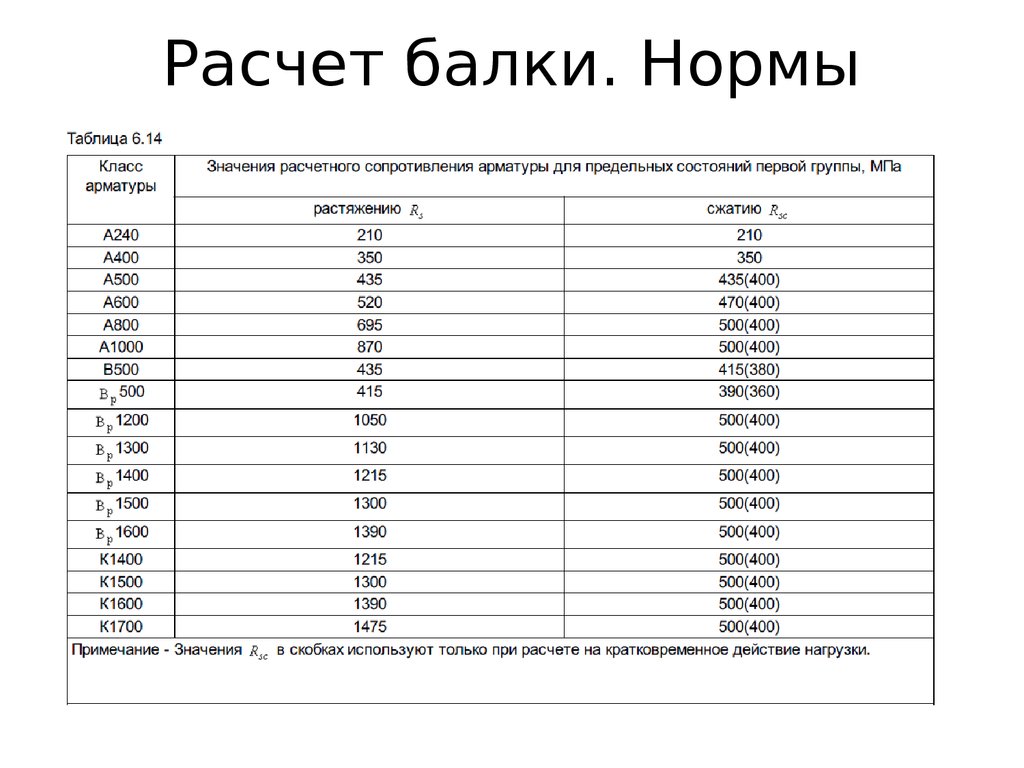

При расчетах может получиться так, что реакция опоры окажется отрицательной. Это означает, что реакция такой опоры направлена вниз (сумма моментов сил, действующих на балку, пытается оторвать её от опоры).

Распределенная нагрузка

В расчетах, иногда требуется задать нагрузку, которая распределена определенным образом по участку длины a. Для вычисления реакций опор такую нагрузку можно заменить её равнодействующей силой. Точкой приложения такой силы считается центр масс распределенной нагрузки, а модуль вычисляется как интеграл от функции распределения нагрузки на заданном участке. Для простых функций модуль легко выразить через заданную интенсивность нагрузки.

Пример системы распределенных нагрузок, действующих на простую балку

В таблице ниже представлены формулы для модуля сосредоточенной равнодействующей силы и точек её приложения для всех видов распределенных нагрузок, поддерживаемых калькулятором:

Нагрузка	Модуль	Точка приложения
Равномерная		1/2 a
Линейно убывающая		1/3 a
Линейно возрастающая		2/3 a

В формулах q — это интенсивность нагрузки в Н/м, a — диапазон действия распределенной нагрузки, точка приложения силы отсчитывается от начала диапазона действия распределенной нагрузки.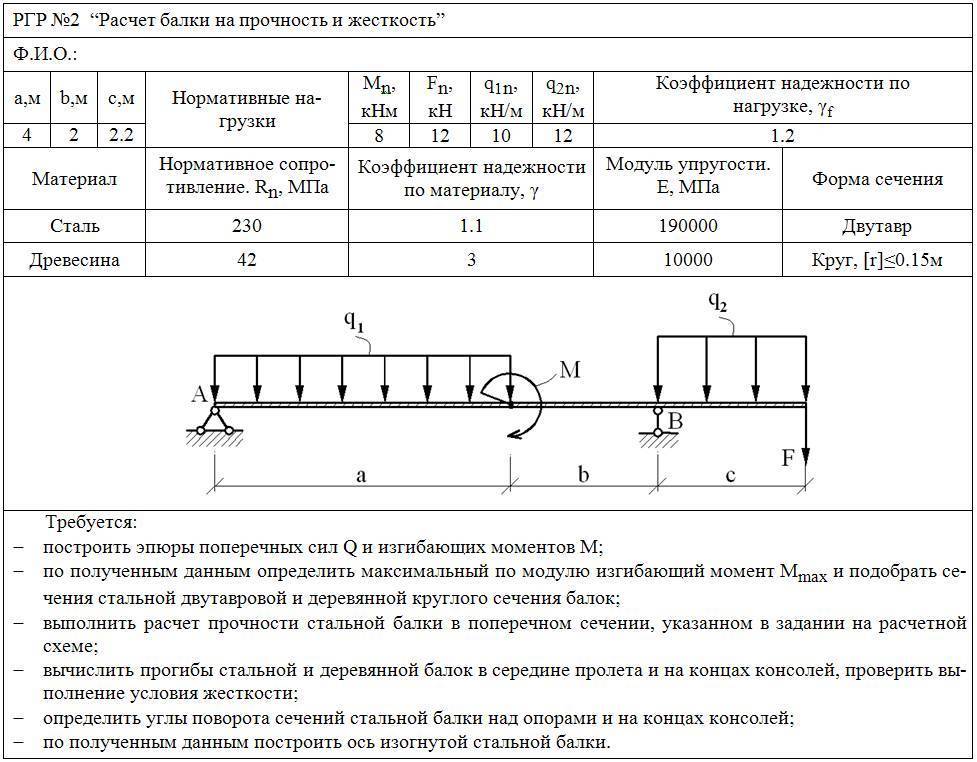 Интенсивность для линейно распределенной нагрузки задается для участка максимума нагрузки ( полагаем, что в точке минимума, интенсивность = 0).
После вычисления модуля и плеча равнодействующей распределенной нагрузки их можно подставить в уравнения моментов, точно так же, как мы это делали с сосредоточенными силами.

Сосредоточенный момент

Еще один способ задания нагрузки в калькуляторе — при помощи момента в Нм, приложенного к некоторой точке. Значение сосредоточенного момента добавляется к уравнениям равновесия со знаком, определяемым направлением момента в соответствии с правилом знаков. Точка приложения сосредоточенного момента для вычисления реакций опор в простой балке значения не имеет.

Вес двутавра – калькулятор, таблицы

Калькулятор веса двутавра использует для расчета табличные значения в соответствии со следующми ГОСТ:

«ГОСТ 8239-89 Двутавры стальные горячекатаные». Используется для классификации балок с уклоном внутренних полок.
«ГОСТ 26020-83 Двутавры стальные горячекатаные с параллельными гранями полок»

Двутавры с параллельными гранями полок имеют следующие разновидности и соответствующие обозначения:

Б – нормальные;
Ш – широкополочные;
К – колонные;
Д – дополнительной серии;

Формула для расчета веса двутавровой балки

Помимо определения веса балки по значениям таблиц ГОСТа, можно воспользоваться следующей формулой:

W = ρ × (2 × b × t + (h — 2 × t) × s) × L

h – высота балки, мм
t – толщина полки, мм
b – ширина полки, мм
s – толщина стенки, мм
ρ – плотность металла

Таблицы размеров и веса двутавровых балок

Двутавр с уклоном полок

Номер двутавра	h	b	s	t	Вес метра, кг	Метров в тонне
10	100	55	4. 5	7.3	9.46	105.71
12	120	64	4.8	7.3	11.5	86.96
14	140	73	4.9	7.5	13.7	72.99
16	160	81	5	7.8	15.9	62.89
18	180	90	5.1	8.1	18. 4	54.35
20	200	100	5.2	8.4	21	47.62
22	220	110	5.4	8.7	24	41.67
24	240	115	5.6	9.5	27.3	36.63
27	270	125	6	9.8	31.5	31.75
30	300	135	6. 5	10.2	36.5	27.4
33	330	140	7	11.2	42.2	23.7
36	360	145	7.5	12.3	48.6	20.58
40	400	155	8.3	13	57	17.54
45	450	160	9	14.2	66. 5	15.04
50	500	170	10	15.2	78.5	12.74
55	550	180	11	16.5	92.6	10.8
60	600	190	12	17.8	108	9.26

Нормальный двутавр (Б)

Номер двутавра	h	b	s	t	Вес метра, кг	Метров в тонне
10Б1	100	55	4.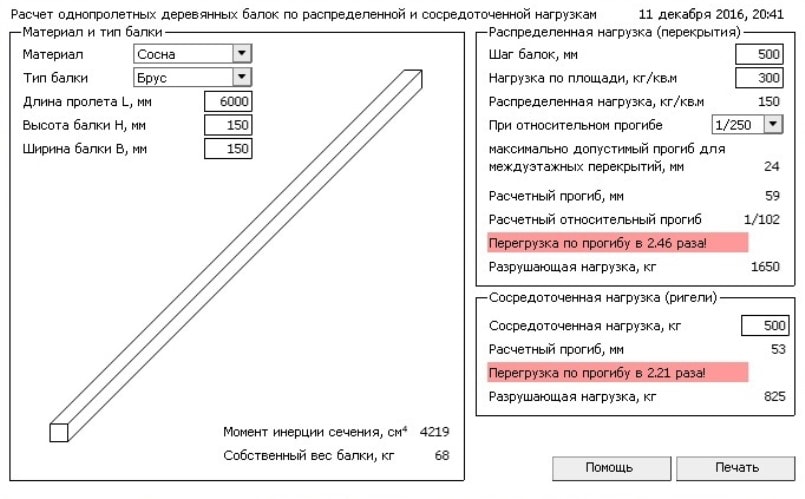 1	5.7	8.1	123.46
12Б1	117.6	64	3.8	5.1	8.7	114.94
12Б2	120	64	4.4	6.3	10.4	96.15
14Б1	137.4	73	3.8	5.6	10.5	95.24
14Б2	140	73	4.7	6.9	12. 9	77.52
16Б1	157	82	4	5.9	12.7	78.74
16Б2	160	82	5	7.4	15.8	63.29
18Б1	177	91	4.3	6.5	15.4	64.94
18Б2	180	91	5.3	8	18.8	53.19
20Б1	200	100	5. 6	8.5	22.4	44.64
23Б1	230	110	5.6	9	25.8	38.76
26Б1	258	120	5.8	8.5	28	35.71
26Б2	261	120	6	10	31.2	32.05
30Б1	296	140	5.8	8.5	32. 9	30.4
30Б2	299	140	6	10	36.6	27.32
35Б1	346	155	6.2	8.5	38.9	25.71
35Б2	349	155	6.5	10	43.3	23.09
40Б1	392	165	7	9.5	48.1	20.79
40Б2	396	165	7. 5	11.5	54.7	18.28
45Б1	443	180	7.8	11	59.8	16.72
45Б2	447	180	8.4	13	67.5	14.81
50Б1	492	200	8.8	12	73	13.7
50Б2	496	200	9.2	14	80. 7	12.39
55Б1	543	220	9.5	13.5	89	11.24
55Б2	547	220	10	15.5	97.9	10.21
60Б1	593	230	10.5	15.5	106.2	9.42
60Б2	597	230	11	17.5	115.6	8.65
70Б1	691	260	12	15. 5	129.3	7.73
70Б2	697	260	12.5	18.5	144.2	6.93
80Б1	791	280	13.5	17	159.5	6.27
80Б2	798	280	14	20.5	177.9	5.62
90Б1	893	300	15	18.5	194	5. 15
90Б2	900	300	15.5	22	213.8	4.68
100Б1	990	320	16	21	230.6	4.34
100Б2	998	320	17	25	258.2	3.87
100Б3	1006	320	18	29	285.7	3.5
100Б4	1013	320	19. 5	32.5	314.5	3.18

Широкополочный двутавр (Ш)

Номер двутавра	h	b	s	t	Вес метра, кг	Метров в тонне
20Ш1	193	150	6	9	30.6	32.68
23Ш1	226	155	6.5	10	36.2	27.62
26Ш1	251	180	7	10	42.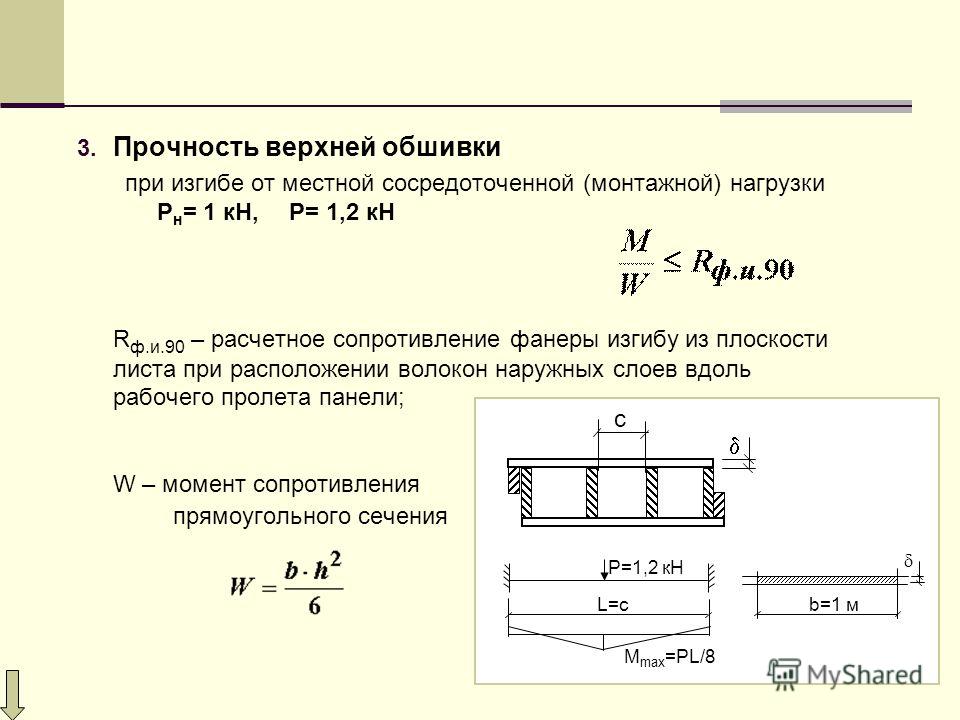 7	23.42
26Ш2	255	180	7.5	12	49.2	20.33
30Ш1	291	200	8	11	53.6	18.66
30Ш2	295	200	8.5	13	61	16.39
30Ш3	299	200	9	15	68.3	14.64
35Ш1	338	250	9. 5	12.5	75.1	13.32
35Ш2	341	250	10	14	82.2	12.17
35Ш3	345	250	10.5	16	91.3	10.95
40Ш1	388	300	9.5	14	96.1	10.41
40Ш2	392	300	11.5	16	111. 1	9
40Ш3	396	300	12.5	18	123.4	8.1
50Ш1	484	300	11	15	114.4	8.74
50Ш2	489	300	14.5	17.5	138.7	7.21
50Ш3	495	300	15.5	20.5	156.4	6.39
50Ш4	501	300	16. 5	23.5	174.1	5.74
60Ш1	580	320	12	17	142.1	7.04
60Ш2	587	320	16	20.5	176.9	5.65
60Ш3	595	320	18	24.5	205.5	4.87
60Ш4	603	320	20	28.5	234. 2	4.27
70Ш1	683	320	13.5	19	169.9	5.89
70Ш2	691	320	15	23	197.6	5.06
70Ш3	700	320	18	27.5	235.4	4.25
70Ш4	708	320	20.5	31.5	268.1	3.73
70Ш5	718	320	23	36. 5	305.9	3.27

Колонный двутавр (К)

Номер двутавра	h	b	s	t	Вес метра, кг	Метров в тонне
20К1	195	200	6.5	10	41.5	24.1
20К2	198	200	7	11.5	46.9	21.32
23К1	227	240	7	10. 5	52.2	19.16
23К2	230	240	8	12	59.5	16.81
26К1	255	260	8	12	65.2	15.34
26К2	258	260	9	13.5	73.2	13.66
26К3	262	260	10	15.5	83.1	12. 03
30К1	296	300	9	13.5	84.8	11.79
30К2	300	300	10	15.5	96.3	10.38
30К3	304	300	11.5	17.5	108.9	9.18
35К1	343	350	10	15	109.7	9.12
35К2	348	350	11	17. 5	125.9	7.94
35К3	353	350	13	20	144.5	6.92
40К1	393	400	11	16.5	138	7.25
40К2	400	400	13	20	165.6	6.04
40К3	409	400	16	24.5	202.3	4. 94
40К4	419	400	19	29.5	242.2	4.13
40К5	431	400	23	35.5	291.2	3.43

Двутавр дополнительной серии (Д)

Номер двутавра	h	b	s	t	Вес метра, кг	Метров в тонне
24ДБ1	239	115	5.5	9.3	27.8	35. 97
27ДБ1	269	125	6	9.5	31.9	31.35
36ДБ1	360	145	12.3	18	49.1	20.37
35ДБ1	349	127	5.8	8.5	33.6	29.76
40ДБ1	399	139	6.2	9	39.7	25.19
45ДБ1	450	152	11	15	52. 6	19.01
45ДБ2	450	180	7.6	13.3	65	15.38
30ДШ1	300.6	201.9	9.4	16	72.7	13.76
40ДШ1	397.6	302	11.5	18.7	124	8.06
50ДШ1	496.2	303.8	14.2	21	155	6. 45

Сварной двутавр (С)

Номер двутавра	h	b	s	t	Вес метра, кг	Метров в тонне
45БС1	444	200	8	12	64.1	15.6
45БС2	460	300	12	20	133.8	7.47
45БСЗ	448	180	8	14	65.9	15. 17
50БС1	482	200	10	16	85.6	11.68
50БС2	482	300	12	16	117.8	8.49
50БСЗ	500	300	12	25	160.1	6.25
50БС4	510	300	14	30	190.8	5.24
55БС1	551	220	10	18	102. 6	9.75
55БС2	547	200	10	16	90.7	11.03
60БС1	577	240	12	16	111.6	8.96
60БС2	585	240	12	20	126.7	7.89
60БСЗ	585	320	12	20	151.8	6.59
60ВС4	595	320	14	25	185. 5	5.39
60БС5	605	320	16	30	219.2	4.56
60БС6	597	190	12	16	101	9.9
70БС1	685	260	12	20	142.4	7.02
70БС2	685	320	14	20	171.4	5.83
70БСЗ	695	320	14	25	196. 5	5.09
70БС4	705	320	16	30	231.7	4.32
70БС5	725	320	20	40	302.2	3.31
70БС6	692	230	12	16	119.9	8.34
80БС1	791	280	14	18	162.1	6.17
80БС2	815	300	18	30	248	4. 03
90БС1	895	300	16	20	201.6	4.96
90БС2	927	300	16	36	276.9	3.61
100БС1	995	320	16	25	244.3	4.09
100БС2	1005	320	16	30	269.4	3.71
100БСЗ	1017	320	20	36	329. 2	3.04
120БС1	1280	400	12	20	242.4	4.13
120БС2	1280	450	14	20	277.6	3.6
140БС1	1440	400	12	20	257.5	3.88
140БС2	1440	450	12	20	273.2	3.66
140БСЗ	1450	500	14	25	350. 1	2.86
160БС1	1640	450	12	20	392	2.55
160БС2	1640	500	12	20	307.7	3.25
160БСЗ	1650	500	14	25	372.1	2.69
160БС4	1650	560	14	25	395.6	2.53
180БС1	1800	560	12	25	384. 6	2.6
180БС2	1800	500	14	25	388.6	2.57
180БСЗ	1810	500	14	30	427.8	2.34
180БС4	1810	600	16	30	502.4	1.99
200БС1	2000	560	12	25	403.5	2.48
200БС2	2010	500	16	30	480. 4	2.08
200БСЗ	2010	600	16	30	527.5	1.9

Двутавр является стандартным профилем конструктивных элементов. Изготавливается из черного металлопроката или древесины. Сечение напоминает букву «Н». Отличительная особенность балки двутаврового профиля заключается в том, что она имеет в 30 раз более жесткую конструкцию и в 7 раз прочнее балки с квадратным профилем, имеющим аналогичное сечение.

Сфера применения двутавров огромна. Их используют, чаще всего, при строительстве, судостроении, мотостроении и т.д. Двутавры позволяют сделать потолочное перекрытие более жестким.

Изготовление металлических двутавров выполняется согласно установленным нормативам и требованиям ГОСТов и ТУ. Поэтому у них регламентированная форма и состав, позволяющие без проблем рассчитать нужные размеры и параметры, включая вес двутавра. Для этого используйте представленные ниже таблицы ГОСТ и калькулятор для автоматического расчета.

Калькулятор веса балки стальной

Лучшее предложение

Загрузите ваш запрос цен на товары в формате exel и получите 5 самых выгодных предложений от поставщиков по каждому товару.

Наименование :	Балка 10 Балка 12 Балка 14 Балка 16 Балка 18 Балка 20 Балка 22 Балка 24 Балка 15К1С Балка 30 Балка 33 Балка 36 Балка 40 Балка 45 Балка 50 Балка 55 Балка 60 Балка 14С Балка 20С Балка 20Са Балка 22С Балка 27С Балка 27Са Балка 36С Балка 23Б1 Балка 24М Балка 30М Балка 36М Балка 45М Балка 10Б1 Балка 12Б1 Балка 14Б1 Балка 14Б2 Балка 16Б1 Балка 16Б2 Балка 18Б1 Балка 18Б2 Балка 20Б1 Балка 26Б1 Балка 26Б2 Балка 25Д2А Балка 30Б2 Балка 31Б1А Балка 35Б2 Балка 40Б1 Балка 40Б2 Балка 41Б2А Балка 45Б2 Балка 50Б1 Балка 50Б2 Балка 55Б1 Балка 55Б2 Балка 60Б1 Балка 60Б2 Балка 70Б1 Балка 70Б2 Балка 80Б1 Балка 80Б2 Балка 90Б1 Балка 90Б2 Балка 100Б1 Балка 100Б2 Балка 100Б3 Балка 100Б4 Балка 20Ш1 Балка 23Ш1 Балка 26Ш1 Балка 26Ш2 Балка 30Ш1 Балка 30Ш2 Балка 30Ш3 Балка 35Ш1 Балка 46Б2А Балка 35Ш3 Балка 40Ш1 Балка 40Ш2 Балка 40Ш3 Балка 50Ш1 Балка 50Ш2 Балка 50Ш3 Балка 50Ш4 Балка 60Ш1 Балка 60Ш2 Балка 60Ш3 Балка 60Ш4 Балка 70Ш1 Балка 70Ш2 Балка 70Ш3 Балка 70Ш4 Балка 70Ш5 Балка 24ДБ1 Балка 27ДБ1 Балка 35ДБ1 Балка 36ДБ1 Балка 40ДБ1 Балка 45ДБ1 Балка 45ДБ2 Балка 30ДШ1 Балка 40ДШ1 Балка 50ДШ1 Балка 20К1 Балка 20К2 Балка 20К3А Балка 23К2 Балка 26К1 Балка 26К2 Балка 26К3 Балка 30К1 Балка 30К2 Балка 30К3 Балка 35К1 Балка 35К2 Балка 35К3 Балка 40К1 Балка 40К2 Балка 40К3 Балка 40К4 Балка 40К5 Балка 20Б1 Балка 25Б1 Балка 25Б2 Балка 30Б1 Балка 30Б2 Балка 20К1 Балка 35Б2 Балка 40Б1 Балка 40Б2 Балка 45Б1 Балка 45Б2 Балка 50Б1 Балка 50Б2 Балка 60Б1 Балка 60Б2 Балка 25Ш1 Балка 36Б3А Балка 30Ш2 Балка 35Ш1 Балка 35Ш2 Балка 40Ш1 Балка 40Ш2 Балка 45Ш1 Балка 50Ш1 Балка 50Ш2 Балка 50Ш3 Балка 50Ш4 Балка 20К2 Балка 25К1 Балка 25К2 Балка 25К3 Балка 30К1 Балка 30К2 Балка 30К4 Балка 35К1 Балка 35К2 Балка 40К1 Балка 40К2 Балка 40К3 Балка 40К4 Балка 40К5 Балка 31У3А Балка 36У2А Балка 41У1А Балка 41У2А Балка 46У3А Балка 61У1А Балка 61У2А Балка 31Б2А Балка 31Б3А Балка 36Б1А Балка 36Б2А Балка 41Б1А Балка 46Б1А Балка 61Б1А Балка 61Б2А Балка 20Д1А Балка 25Д3А Балка 12КС Балка 15К1А Балка 15К2А Балка 15К3А Балка 20К2А Балка 20К4А Балка 20К5А Балка 20К4С Балка 25К1АС Балка 25К4С Балка 30К3С Балка 31К1АС Балка 31К3АС Балка 35К3С Балка 35К4С Балка 40К9С Балка 30Ш2С Балка 50Ш2С
Длина в метрах
Цена за 1 кг. Цена за 1 тонну Цена за 1 метр погонный
Вес 1 го метра :
Стоимость

Теоретический вес 1 метра = R*b*t+s*(h-t),

h — высота двутавра;
b — ширина полки;
S — толщина стенки;
t — средняя толщина полки;
R — радиус внутреннего закругления;
r — радиус закругления полки.

Нередко случаются ситуации, когда использование металлических балок наиболее целесообразно. Например, в строительстве для перекрытия большого пролета металлические балки становятся прекрасной альтернативой деревянным балкам большого сечения.

Использование стальной двутавровой балки обеспечит максимальную прочность и высокие эксплуатационные характеристики перекрытия.

При этом срок службы стальной балки вдвое выше аналогичных деревянных изделий.

Введите необходимые параметры, и калькулятор выполнит расчет веса металлической балки. Для того чтобы рассчитать прогиб металлической балки используйте специализированный онлайн-калькулятор.

Зная вес и прочность изделия, можно выполнить расчет эксплуатационной нагрузки на металлическую балку.

Данный онлайн-калькулятор позволит выполнить точный расчет веса металлической балки и одновременно просчитать стоимость материалов.

Калькулятор подходит также для расчёта двутавровой металлической балки, используемой для межэтажного перекрытия.

Расчет общего веса материалов поможет вам оптимизировать затраты на перевозку.

ГОСТ 8239-89

Двутавры стальные горячекатаные

СТО АСЧМ 20-93 Двутавры горячекатаные с параллельными гранями полок

ГОСТ 26020-83 Двутавры стальные горячекатаные с параллельными гранями полок

Таблицы веса стальных балок двутаврового и таврового сечения

Возврат к списку

Расчет балки на прогиб и прочность

Информация

Балка занимает роль основополагающего элемента в несущей конструкции. Её функция приравнивается к стержню всей конструкции, который прочно закрепили. При строительстве какого-либо сооружения очень важно осуществить грамотный расчет балки на прогиб и исключить допущение ошибки в расчетах. Прежде всего расчет требуется для определения того, на сколько балка деформируется в процессе эксплуатации сооружения. Если при расчете показатель деформации находится в пределах нормы, то можно определить нужные показатели будущей балки (сечение, материал, размер и так далее).
Делая расчет балки на прочность, необходимо четко знать виды материала, из которого изготавливаются балки (сталь, дерево, бетон, алюминий, стекло и медь). Далее нужно обратить внимание на то, что типы нагрузок, как и их схемы также различаются. Так, например, распределенная нагрузка означает, что давление оказывается не на одну точку, а распределено по всей площади балки. Сосредоточенный тип нагрузки характеризует направленность давления на один небольшой участок (точку) балки.

Назначение калькулятора

Калькулятор для расчёта железобетонных балок перекрытий предназначен для определения габаритов, конкретного типа и марки бетона, количества и сечения арматуры, требующихся для достижения балкой максимального показателя выдерживаемой нагрузки.

Соответственно СНиП 2.03.01-84 «Бетонные и железобетонные конструкции» габариты железобетонных балок перекрытия и их устройство подсчитываются по дальнейшим принципам:

Минимальная высота балки перекрытия должна составлять не меньше 1/20 части длины перекрываемого проёма. К примеру при длине проёма в 5 м минимальная высота балок должна составлять 25 см;
Ширина железобетонной балки устанавливается по соотношению высоты к ширине в коэффициентах 7:5;
Армировка балки состоит минимум из 4 арматур – по два прута снизу и сверху. Применяемая арматура должна составлять не меньше 12 мм в диаметре. Нижнюю часть балки можно армировать прутами большего сечения, чем верхнюю;
Железобетонные балки перекрытия бетонируются без перерывов заливки, одной порцией бетонной смеси, чтобы не было расслоения бетона.

Дистанцию между центрами укладываемых балок определяют длиной блоков и установленной шириной балок. К примеру, длина блока составляет 0,60 м, а ширина балки 0,15. Дистанция между центрами балок будет равна – 0,60+0,15=0,75 м.

Вместе с типами, существуют четыре схемы нагрузок:

Шарнир-Шарнир
Заделка-Шарнир
Заделка-Заделка»
Свободный конец

Наш онлайн калькулятор позволяет сделать расчет, комбинируя все виды балок, типы и схемы нагрузок, при этом абсолютно исключив вероятность допущения ошибки в процессе расчета. Обычно рассчитывают деревянные балки, а также металлические. В процессе вычисления показателя определяется сумма сил, воздействующих на балку, которые направлены перпендикулярно конструкции. Расчет деревянной балки на прогиб осуществляется с учетом материала, т.е. учитывают вид древесины, её гибкость и многие другие параметры, также важно учесть форму сечения балки и нагрузка какого вида оказывается на балку. Сравнивая с расчетом балки из древесины, расчет металлической балки на прогиб существенно отличается, поскольку важное внимание уделяют виду соединения: электросварка, заклепки, болты и другие виды соединений.

Все перечисленные выше нюансы позволяют понять, что расчет балки на прогиб — крайне ответственный этап в процессе стройки какого-либо объекта. От него зависит надежность, долговечность и целостность всей конструкции. Наш калькулятор позволит Вам быстро и безошибочно провести предельно точный расчет.

Принцип работы

Согласно ГОСТ 26519-85 «Конструкции железобетонные заглублённых помещений с перекрытием балочного типа. Технические условия» формула расчёта полезной нагрузки железобетонных балок перекрытия складывается из следующих характеристик:

Нормативно-эксплуатационная нагрузка на балки перекрытия с определённым коэффициентным запасом. Для жилых зданий данный показатель нагрузки составляет 151 кг на м2, а коэффициентный запас равен 1,3. Получаемая нагрузка – 151*1,3=196,3 кг/м2;
Нагрузка от общей массы блоков, которыми закладываются промежутки между балками. Блоки из лёгких материалов, к примеру из пенобетона или газобетона, показатель плотности которых D-500, а толщина 20 см будут нести нагрузку – 500*0,2=100 кг/м2;
Испытываемая нагрузка от массы армированного каркаса и последующей стяжки. Вес стяжки с толщиной слоя 5 см и показателем плотности 2000 кг на м3 будет образовывать следующую нагрузку – 2000*0,05=100 кг/м2 (масса армировки добавлена в плотность бетонной смеси).

Показатель полезной нагрузки железобетонной балки перекрытия составляется из суммы всех трёх перечисленных показателей – 196,3+100+100=396,3 кг/м2.

Разновидности балок, применяемых в строительстве

Современная стройиндустрия при возведении сооружений промышленного и жилого назначения, практикует использование стержневых систем различного сечения, формы и длины, изготовленных из различных материалов.

Наиболее большее распространение получили стальные и деревянные изделия. В зависимости от используемого материала, определение значения прогиба имеет свои нюансы, связанные со структурой и однородностью материала.

Деревянные

Современное малоэтажное строительство индивидуальных домов и загородных коттеджей практикует широкое использование лаг, изготовленных из хвойных и твердых пород древесины.

В основном, деревянные изделия, работающие на изгиб, применяются для обустройства напольных и потолочных перекрытий. Именно эти элементы конструкции испытают наибольшее действие поперечных нагрузок, взывающих наибольший прогиб.

Стрела прогиба деревянной лаги зависит:

От материала (породы древесины), который использовался при изготовлении балки.
От геометрических характеристик и формы попечённого сечения расчетного объекта.
От совокупного действия различного вида нагрузок.

Критерий допустимости прогиба балки учитывает два фактора:

Соответствие реального прогиба предельно допустимым значениям.
Возможность эксплуатации конструкции при наличии расчетного прогиба.

Стальные

Имеют более сложное сечение, которое может быть составным, выполненным из нескольких видов металлического проката. При расчете металлоконструкций, помимо определения жесткости самого объекта его элементов, часто появляется необходимость определения прочностных характеристик соединений.

Обычно, соединение отдельных элементов стальной металлоконструкции проводится:

С использованием электросварки.
Путем применения резьбовых (шпилечных, болтовых и винтовых) соединений.
Соединением заклепками.

Расчет опорных реакций балки на двух опорах онлайн

Расчет выполняется по следующей методике:

1. Заменяем распределенную нагрузку ее равнодействующей, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка L, на котором она действует: Fq = q*L.

2. Обозначаем опоры. Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно-неподвижную и одну шарнирно-подвижную опоры.

3. Освобождаемся от опор и заменяем их действие на балку реакциями. Реакции опор при такой нагрузке будут только вертикальными.

4. Составляем уравнения равновесия вида: MA = 0; MB = 0, Моментом силы относительно точки называется произведение этой силы на плечо — кратчайшее расстояние от этой точки приложения силы (в общем случае — до линии действия силы).

5. Выполним проверку решения. Для этого составим уравнение равновесия: Y = 0, Если оно удовлетворено, то реакции найдены правильно, а если нет, но в решении допущена ошибка.

6. Строим эпюру поперечных сил Qx. Для этого определяем значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот. В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно Qлев и Qправ. Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правилам: а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии; б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию. Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Qx.

7. Строим эпюру изгибающих моментов Мx. Для этого определяем изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против — отрицательным (со знаком «минус»), а для правой части наоборот. В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее. Изгибающие моменты в этих точках обозначаются соответственно Млев и Мправ. В точках приложения сил определяется одно значение изгибающего момента. Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами: а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией; б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.
Пример решения балки:

Перечень расчетов

Главная страница | Общие данные | Перечень расчетов | Форум

(Архив устаревших расчетов)

Шифр	Актуальность	Наименование расчета	Нормативное обоснование	Версия
КЖ — Конструкции железобетонные
Изгиб:
КЖ-01	Проверка прочности изгибаемого железобетонного элемента	СП 63.13330.2012 пп.8.1.8-8.1.13
КЖ-02	Подбор требуемой арматуры для изгибаемого ж.б. элемента	СП 63. 13330.2012 пп.8.1.8-8.1.13
КЖ-08	Проверка прочности бетонного (не железобетонного) элемента на изгиб	СП 63.13330.2012; СП 29.13330.2011
Внецентренное сжатие и растяжение:
КЖ-03	Внецентренно сжатый элемент
КЖ-05.1	Проверка прочности сечения при внецентренном сжатии (в двух плоскостях)	Пособие к СП 52-101-2003
КЖ-11	Проверка прочности внецентренно растянутого элемента	СП 63.13330.2012
КЖ-14	Расчет ж.б. стойки круглого либо кольцевого сечения	СП 63.13330.2012 прил. Д
Продавливание и поперечная сила:
КЖ-07.3	Колонна посередине плиты	СП 63.13330.2012 п.8.1.46-8.1.52
КЖ-07.5	Колонна рядом с краем плиты	СП 63.13330.2012 п.8.1.46-8.1.52
КЖ-07.6	Колонна рядом с углом плиты	СП 63.13330.2012 п.8.1.46-8. 1.52
КЖ-07.7	Колонна посередине плиты с отверстием	СП 63.13330.2012 п.8.1.46-8.1.52
КЖ-07.8	Круглая колонна посередине плиты	СП 63.13330.2012 п.8.1.46-8.1.52
КЖ-08	Расчет на действие поперечной силы	СП 63.13330.2012 п.п. 8.1.32 — 8.1.35
КЖ-12	Расчет ж.б. конструкции на местное сжатие	СП 63.13330.2012 п.п. 8.1.43-45
Прогиб и трещиностойкость:
КЖ-04	Проверка на образование трещин и расчет ширины их раскрытия	СП 63.13330.2012
КЖ-09	Расчет прогиба ж.б. элемента (упрощенный)	СП 63.13330.2012
КЖ-10	Расчет прогиба ж.б. элемента (полноценный)	СП 63.13330.2012
Конструктивные требования:
КЖ-06	Определение расчетной длины анкеровки/нахлестки арматуры	СП 63.13330.2012
Расчеты по Eurocode2:
EC2-1	Прогиб ж. б. балки тавровго сечения по Eurocode2	Eurocode2 (EN1992-1-1:2004)
EC2-2	Deflection calculation for reinforced concrete T-beam	Eurocode2 (EN1992-1-1:2004)
КМ — Конструкции металлические
Изгиб:
КМ-04	Проверка балки по прочности и прогибу	СНиП II-23-81
КМ-01	Расчет устойчивости плоской формы деформирования при изгибе	СНиП II-23-81
КМ-06	Расчет профилированного настила	Пособие к СНиП II-23-81
Центральное в внецентренное сжатие:
КМ-02	Центрально сжатый элемент	СНиП II-23-81
Соединения:
КМ-05	Расчет сварного соединения (ручная сварка)	СНиП II-23-81
КМ-07	Расчет узлов ферм из прямоугольных профилей	СП 16.13330.2011 прил.Л
ОиФ — Основания и фундаменты
Фундаменты мелкого заложения:
ОФ-01. 2	Расчетное сопротивление основания	СП 22.13330.2011
ОФ-02.1	Напряжение под подошвой прямоугольного фундамента мелкого заложения
ОФ-02.2	Напряжение под подошвой круглого фундамента мелкого заложения
ОФ-03.2	Осадка фундамента мелкого заложения	СП 22.13330.2011
ОФ-09	Расчет крена фундамента мелкого заложения	СП 22.13330.2011, п.п.5.6.43-5.6.45
ОФ-10	Проверка слабого подстилающего слоя	СП 22.13330.2011 п.п.5.6.7, 5.6.25
Свайные фундаменты:
ОФ-04.3	Несущая способность забивной висячей сваи	СП 24.13330.2011
ОФ-10	Несущая способность буровой висячей сваи	СП 24.13330.2011
ОФ-06.1	Осадка одиночной сваи	СП 24.13330.2011, п.п. 7.4.2–7.4.3
ОФ-06. 2	Дополнительная осадка сваи (взаимовлияние)	СП 24.13330.2011, п.п. 7.4.4
ОФ-07	Расчет осадки свайного фундамента (куста свай)	СП 24.13330.2011, п.п. 7.4.4–7.4.5
ОФ-08.1	Несущая способность сваи по результатам испытаний динамической нагрузкой (при sa ≥0.002 м)	СП 24.13330.2011, п. 7.3.7
ОФ-08.2	Несущая способность сваи по результатам испытаний динамической нагрузкой (при sa <0.002 м)	СП 24.13330.2011, п. 7.3.7
ОФ-11	Вычисление усилий в сваях	СП 24.13330.2011
ОФ-12	Расчет сваи на горизонтальную нагрузку	СП 50-102-2003 прил.Д; СП 24.13330.2011 прил.В
НиВ — Нагрузки и воздействия
НВ-01	Расчет ветровых нагрузок	СП 20.13330.2011
НВ-02	Расчет снеговых мешков	СП 20.13330.2016, п.Б.8
АР — Расчеты в рамках марки АР
АР-01	Теплотехнический расчет	СНиП 23-02-2003
Прочее
Линейная интерполяция
Калькулятор арматуры
Сортаменты металлопроката
Конвертор единиц измерения

Рассчитываем вес балки, применяя онлайн калькулятор

Скачать калькулятор балки онлайн и бесплатно получить код можно на этой странице

Балка как металлический профиль

Этот вид металлопроката можно отнести к специальному, особому виду прокатных изделий, который используется для изготовления металлоконструкций, которые будут соответствовать всем необходимым техническим требованиям при эксплуатации.

Балка изготавливается из специальной стали, углеродистой или низколегированной. Способ её изготовления – при помощи литья в формы, прокат заготовки горячим или холодным способом.

Её профиль считается сложным, поэтому при её изготовлении затрачивается времени гораздо больше, чем при изготовлении, например, уголка.

Так как балка выполняет очень важную задачу, становясь основой или скелетом для будущего сооружения, к ней предъявляются особые требования, которые зависят от качества изготовления балки.

Виды балок, которые выпускаются из металлопроката

На самом деле существует несколько видов балок, но наиболее востребованными считаются: профиль в буквы «Т», называемый тавровым и профиль в виде буквы «Н» или соединёнными буквами «Т», то есть двутавровыми.

Выбирая тот или другой профиль балки, нужно просчитать наибольшую нагрузку, которую она сможет нести. Для этого используют расчеты, которые есть в формулах по сопромату. Можно использовать онлайн – калькулятор для расчета, который имеется на сайте.

В основном этот вид проката испытывает нагрузку на изгиб и нагрузку на ось. Но не нужно забывать, что при таком виде нагрузок появляется крутящийся момент, который также нужно учитывать при выборе профиля.

По данным расчета выбирают форму сечения, его размеры и материал, из которого изготовлен прокат. Площадь сечения является основным критерием расчета.

По форме сечения они бывают следующие:

Обычные тавровые балки и двухскатные, которые используются между опорами, имеющими среднее расстояние друг от друга.
Двутавровая балка, которая используется между опорами с максимально длинным расстоянием, имеет повышенную стойкость на изгиб.
Балка с сечением в виде прямоугольника, которая используется между опорами с небольшим расстоянием друг от друга. Также применяется в случае, когда крутящийся момент на опору будет увеличен.
Балка с сечением в виде буквы «Г», применяется для фасадов, применение не столь частое.

В свою очередь, двутавровые балки также имеют свои разновидности:

Двутавр, который имеет угол наклона граней полок 6 – 12 градусов. Изготавливается согласно ГОСТа 8239-89.
Двутавр с параллельными гранями полок. Он изготавливается согласно ГОСТа 26020-83 и СТО АСЧМ-20-93.
Двутавр специальный, который изготавливается по ГОСТу 19425-74 и делится, в свою очередь на тип «М» с углом наклоном граней до 12 градусов и тип «С» с углом наклона граней до 16 градусов.
Тавр изготавливается согласно ТУ 14-2-685-86.

Двутавровая балка, общий вид

Промышленность также впускает составные балки, которые изготавливаются на предприятии сварным способом или при помощи болтов.

Также этот прокат разделяется по ассортименту для удобства выбора со склада:

Б – стандартный вид балок;
Ш– широкополочный вид балок;
К– балки колонные двутавровые специальные.

Нормативы по которым выпускается прокат

Выпуск каждого вида проката строго регламентируется государственным стандартом, в котором указаны и размеры проката – величина углов, ширина полок, наклон граней и все размеры, которые входят в площадь поперечного сечения, а также длина проката. Кроме этого регламентируется материал, из которого он изготовлен, а также его технические характеристики.

Общие технические условия для металлопроката оговорены в ГОСТе 27772-88.

По горячекатаному двутавру из стали нужно руководствоваться ГОСТ 8239-89, который разработан для горячекатаных стальных профилей, имеющих уклон внутренних граней полок.

Сечение горячекатаной балки по ГОСТ 8239-89

Согласно ГОСТа:

h – высота двутавра,
b – ширина полки,
s – толщина стенки,
t – средняя толщина полки,
R – радиус внутреннего закругления,
r- радиус закругления полки.

В этом же документе отражены и пределы отклонений при изготовлении профиля.

На основании этого и ряда других ГОСТов был принят ГОСТ 5350-2005, который регламентирует технические условия для проката из стали углеродистой, в том числе и на прокат балки двутавровой, как стандартной, так и специального назначения. Механические свойства стали должны соответствовать таким параметрам, как временное сопротивление, предел текучести, ударной вязкости и другим параметрам, которые указаны в этом ГОСТе.

Двутавры стальные горячекатаные по ГОСТ 8239-89. Профили и их вес

Наименование профиля двутавра	Высота (h), мм	Ширина полки (b), мм	Толщина стенки (s), мм	Средняя толщина полки (t), мм	Масса 1 м балки, кг	Метров балки в тонне
Балка 10	100	55	4.5	7.2	9.46	105.71
Балка 12	120	64	4.8	7.3	11.5	86.96
Балка 14	140	73	4. 9	7.5	13.7	72.99
Балка 16	160	81	5	7.8	15.9	62.89
Балка 18	180	90	5.1	8.1	18.4	54.35
Балка 20	200	100	5.2	8.4	21	47.62
Балка 22	220	110	5.4	8.7	24	41.67
Балка 24	240	115	5.6	9.5	27.3	36.63
Балка 27	270	125	6	9.8	31.5	31.75
Балка 30	300	135	6.5	10.2	36.5	27.4
Балка 33	330	140	7	11.2	42.2	23.7
Балка 36	360	145	7.5	12.3	48.6	20.58
Балка 40	400	155	8. 3	13	57	17.54
Балка 45	450	160	9	14.2	66.5	15.04
Балка 50	500	170	10	15.2	78.5	12.74
Балка 55	550	180	11	16.5	92.6	10.8
Балка 60	600	190	12	17.8	108	9.26

ГОСТ 19425-74, в котором указаны параметры для выпуска специальных балок «М» и»С». Серия «М» применяется для подвесных путей, а серия «С» для оборудования шахтных проходов, причем по точности они могут изготовляться как высокой точности – маркируются буквой «А» и обычной точности- маркируются буквой «В».

Балка двутавровая по ГОСТ 19425-74. Профили и вес

Наименование профиля двутавра	Высота (h), мм	Ширина полки (b), мм	Толщина стенки (s), мм	Средняя толщина полки (t), мм	Масса 1 м балки, кг	Метров балки в тонне
Балка 14С	140	80	5. 5	9.1	16.9	59.17
Балка 20С	200	100	7	11.4	27.9	35.84
Балка 20Са	200	102	9	11.4	31.1	32.15
Балка 22С	220	110	7.5	12.3	33.1	30.21
Балка 27С	270	122	8.5	13.7	42.8	23.36
Балка 27Са	270	124	10.5	13.7	47	21.28
Балка 36С	360	140	14	15.8	71.3	14.03
Балка 18М	180	90	7	12	25.8	38.76
Балка 24М	240	110	8.2	14	38.3	26.11
Балка З0М	300	130	9	15	50.2	19.92
Балка 36М	360	130	9. 5	16	57.9	17.27
Балка 45М	450	150	10.5	18	77.6	12.89

Балки с параллельными гранями полок имеют свой ГОСТ 26020-83

По обозначению: h – высота двутавра, b – ширина полки двутавра, s – толщина основной стенки, t – толщина полки, r – радиус сопряжения.

Двутавры стальные горячекатаные с параллельными гранями полок по ГОСТ 26020-83

Наименование профиля двутавра	Высота (h), мм	Ширина полки (b), мм	Толщина стенки (s), мм	Средняя толщина полки (t), мм	Масса 1 м балки, кг	Метров балки в тонне
			Нормальные двутавры
Балка 10Б1	100	55	4.1		8.1	123.46
Балка 12Б1	117. 6	64	3.8		8.7	114.94
Балка 12Б2	120	64	4.4		10.4	96.15
Балка 14Б1	137.4	73	3.8		10.5	95.24
Балка 14Б2	140	73	4.7		12.9	77.52
Балка 16Б1	157	82	4		12.7	78.74
Балка 16Б2	160	82	5		15.8	63.29
Балка 18Б1	177	91	4.3		15.4	64.94
Балка 18Б2	180	91	5.3		18.8	53.19
Балка 20Б1	200	100	5.6		22.4	44.64
Балка 23Б1	230	110	5.6		25.8	38.76
Балка 26Б1	258	120	5.8		28	35. 71
Балка 26Б2	261	120	6		31.2	32.05
Балка 30Б1	296	140	5.8		32.9	30.4
Балка 30Б2	299	140	6		36.6	27.32
Балка 35Б1	346	155	6.2		38.9	25.71
Балка 35Б2	349	155	6.5		43.3	23.09
Балка 40Б1	392	165	7		48.1	20.79
Балка 40Б2	396	165	7.5		54.7	18.28
Балка 45Б1	443	180	7.8		59.8	16.72
Балка 45Б2	447	180	8.4		67.5	14.81
Балка 50Б1	492	200	8.8		73	13.7
Балка 50Б2	496	200	9. 2		80.7	12.39
Балка 55Б1	543	220	9.5		89	11.24
Балка 55Б2	547	220	10		97.9	10.21
Балка 60Б1	593	230	10.5		106.2	9.42
Балка 60Б2	597	230	11		115.6	8.65
Балка 70Б1	691	260	12		129.3	7.73
Балка 70Б2	697	260	12.5		144.2	6.93
Балка 80Б1	791	280	13.5		159.5	6.27
Балка 80Б2	798	280	14		177.9	5.62
Балка 90Б1	893	300	15		194	5.15
Балка 90Б2	900	300	15.5		213.8	4.68
Балка 100Б1	990	320	16		230. 6	4.34
Балка 100Б2	998	320	17		258.2	3.87
Балка 100Б3	1006	320	18		285.7	3.5
Балка 100Б4	1013	320	19.5		314.5	3.18
			Широкополочные двутавры
Балка 20Ш1	193	150	6		30.6	32.68
Балка 23Ш1	226	155	6.5		36.2	27.62
Балка 26Ш1	251	180	7		42.7	23.42
Балка 26Ш2	255	180	7.5		49.2	20.33
Балка 30Ш1	291	200	8		53.6	18.66
Балка 30Ш2	295	200	8.5		61	16.39
Балка 30Ш3	299	200	9		68. 3	14.64
Балка 35Ш1	338	250	9.5		75.1	13.32
Балка 35Ш2	341	250	10		82.2	12.17
Балка 35Ш3	345	250	10.5		91.3	10.95
Балка 40Ш1	388	300	9.5		96.1	10.41
Балка 40Ш2	392	300	11.5		111.1	9
Балка 40Ш3	396	300	12.5		123.4	8.1
Балка 50Ш1	484	300	11		114.4	8.74
Балка 50Ш2	489	300	14.5		138.7	7.21
Балка 50Ш3	495	300	15.5		156.4	6.39
Балка 50Ш4	501	300	16.5		174.1	5.74
Балка 60Ш1	580	320	12		142. 1	7.04
Балка 60Ш2	587	320	16		176.9	5.65
Балка 60Ш3	596	320	18		205.5	4.87
Балка 60Ш4	603	320	20		234.2	4.27
Балка 70Ш1	683	320	13.5		169.9	5.89
Балка 70Ш2	691	320	15		197.6	5.06
Балка 70Ш3	700	320	18		235.4	4.25
Балка 70Ш4	708	320	20.5		268.1	3.73
Балка 70Ш5	718	320	23		305.9	3.27
			Колонные двутавры
Балка 20К1	195	200	6.5		41.5	24.1
Балка 20К2	198	200	7		46. 9	21.32
Балка 23К1	227	240	7		52.2	19.16
Балка 23К2	230	240	8		59.5	16.81
Балка 26K1	255	260	8		65.2	15.34
Балка 26K2	258	260	9		73.2	13.66
Балка 26K3	262	260	10		83.1	12.03
Балка 30К1	296	300	9		84.8	11.79
Балка 30К2	304	300	10		96.3	10.38
Балка 30К3	300	300	11.5		108.9	9.18
Балка 35К1	343	350	10		109.7	9.12
Балка 35К2	348	350	11		125.9	7.94
Балка 35К3	353	350	13		144. 5	6.92
Балка 40К1	393	400	11		138	7.25
Балка 40К2	400	400	13		165.6	6.04
Балка 40К3	409	400	16		202.3	4.94
Балка 40К4	419	400	19		242.2	4.13
Балка 40К5	431	400	23		291.2	3.43
			Двутавры дополнительной серии (Д)
Балка 24ДБ1	239	115		5.5	27.8	35.97
Балка 27ДБ1	269	125		6	31.9	31.35
Балка 36ДБ1	360	145		7.2	49.1	20.37
Балка 35ДБ1	349	127		5.8	33.6	29.76
Балка 40ДБ1	399	139		6. 2	39.7	25.19
Балка 45ДБ1	450	152		7.4	52.6	19.01
Балка 45ДБ2	450	180		7.6	65	15.38
Балка 30ДШ1	300.6	201.9		9.4	72.7	13.76
Балка 40ДШ1	397.6	302		11.5	124	8.06
Балка 50ДШ1	496.2	303.8		14.2	155	6.45

Если на двутавр существуют ГОСТ ы, то изготовление тавровой балки осуществляется по ТУ 14-2-685-86

Обозначение здесь такое же, как и у двутавровой балки.

Тавры колонные и Тавры ШТ по ТУ 14-2-685-86 имеют следующие размеры

Тавры ШТ по ТУ 14-2-685-86. Наименование профиля, вес.

Наименование профиля двутавра	Высота (h), мм	Ширина полки (b), мм	Толщина стенки (s), мм	Средняя толщина полки (t), мм	Масса 1 м балки, кг	Метров балки в тонне
Балка 13ШТ1	122	180	7	10	21. 1	47.39
Балка 13ШТ2	124	180	7.5	12	24.4	40.98
Балка 15ШТ1	142	200	8	11	26.6	37.59
Балка 15ШТ2	144	200	8.5	13	30.2	33.11
Балка 15ШТ3	146	200	9	15	33.9	29.5
Балка 17,5ШТ1	165.5	250	9.5	12.5	37.3	26.81
Балка 17,5ШТ2	167	250	10	14	40.8	24.51
Балка 17,5ШТ3	169	250	10.5	16	45.4	22.03
Балка 20ШТ1	190.5	300	9.5	14	47.8	20.92
Балка 20ШТ2	192.5	300	11.5	16	55.2	18.12
Балка 20ШТ3	194. 5	300	12.5	18	61.3	16.31
Балка 25ШТ1	238.5	300	11	15	56.9	17.57
Балка 25ШТ2	241	300	14.5	17.5	68.9	14.51
Балка 25ШТ3	244	300	15.5	20.5	77.7	12.87
Балка 25ШТ4	247	300	16.5	23.5	86.6	11.55
Балка 30ШТ1	286.5	320	12	17	70.7	14.14
Балка 30ШТ2	290	320	16	20.5	80	12.5
Балка 30ШТ3	294	320	18	24.5	102.3	9.78
Балка 30ШТ4	298	320	20	28.5	116.5	8.58

Тавры колонные по ТУ 14-2-685-86. Название профиля и вес

Тавры колонные по ТУ 14-2-685-86.

Название профиля и вес

Наименование профиля двутавра	Высота (h), мм	Ширина полки (b), мм	Толщина стенки (s), мм	Средняя толщина полки (t), мм	Масса 1 м балки, кг	Метров балки в тонне
Балка 10KT1	94	200	6.5	10	20.6	48.54
Балка 10KT2	95.5	200	7	11.5	23.2	43.1
Балка 11,5KT1	110	240	7	10.5	25.9	38.61
Балка 11,5KT2	111.5	240	8	12	29.5	33.9
Балка 13KT1	124	260	8	12	32.4	30.86
Балка 13KT2	125.5	260	9	13.5	36.3	27.55
Балка 13KT3	127.5	260	10	15.5	41.3	24. 21
Балка 15KT1	144.5	300	9	13.5	42.1	23.75
Балка 15KT2	146.5	300	10	15.5	47.9	20.88
Балка 15KT3	148.5	300	11	17.5	54.1	18.48
Балка 17,5KT1	168	350	10	15	54.6	18.32
Балка 17,5KT2	170.5	350	11	17.5	62.6	15.97
Балка 20KT1	193	400	11	16.5	68.7	14.56
Балка 20KT2	196.5	400	13	20	82.4	12.14

Применение балок в промышленности

Балка, как наиболее мощный металлопрокат, используется в различных областях. В строительстве она выступает как основа перекрытий, перераспределяя нагрузку с перекрытия на несущие конструкции и далее на фундамент. Из неё строится основа здания, которую затем обшивают другими элементами.

Тавровая балка выдерживает меньшую нагрузку, но она также очень востребована. Балки и двойная и одинарная необходима при строительстве мостов, тоннелей, складов, ну и естественно, при строительстве зданий, как жилых, так и промышленных.

Специальные балки с повышенной прочностью используют в качестве монорельса для подъемного оборудования и для строительства туннелей шахт, при строительстве метро и тому подобных ответственных сооружений.

Одно из хороших качеств горячекатаных балок можно назвать то, что они менее подвержены коррозии по сравнению с холоднокатаными.

Балка может быть изготовлена из алюминиевого сплава, в тех случаях, когда нужна лёгкость конструкции. При этом прочность её достаточно высокая.

Поставщики металлопроката

В России есть много металлургических заводов, около 60, но балки выпускают только некоторые из них.

Например, выпускает балку Алапаевский металлургический завод в числе остальных прокатных изделий, Магнитогорский металлургический комбинат выпускает балку горячекатаную, Белорецкий металлургический комбинат, Челябинский металлургический комбинат, Петровск – Забайкальский завод, Оскольский электрометаллургический завод, Омутнинский металлургический комбинат. Другие предприятия выпускают этот прокат при наличии соответствующего заказа, конечно заказ должен быть большим. Так как балка это продукция со специфическими свойствами, её иногда закупают за рубежом.

Заказ балки можно сделать как на предприятии, так и у металлотрейдеров, поставляющих металлопрокат, в Москве их есть много. Желательно работать с крупными организациями, у которых высокий рейтинг.

Для заказа продукции нужно высчитать вес балки. По приведенным здесь размерам выбираете вес одного погонного метра балки нужно вам профиля. Потом вес 1 метра погонного умножаем на длину проката, то есть балки. Для простоты расчета предлагаем использовать наш онлайн калькулятор веса, пользоваться которым очень просто и надёжно. Результат получаете мгновенно.

Расчёт железобетонной балки

Не смотря на то, что заводы железобетонных изделий производят большое количество готовой продукции, все же иногда приходится делать железобетонную балку перекрытия или железобетонную перемычку самому. Практически все видели строителей-монтажников, засовывающих в опалубку какие-то железяки, и почти все знают, что это — арматура, обеспечивающая прочность конструкции, вот только определять количество и диаметр арматуры, закладываемой в железобетонные конструкции, хорошо умеют только инженеры-технологи. Железобетонные конструкции, хотя и применяются вот уже больше сотни лет, но по-прежнему остаются загадкой для большинства людей, точнее, не сами конструкции, а расчет железобетонных конструкций.

Расчёт железобетонной балки — это одна из наиболее часто встречающихся задач в частном секторе. Столкнувшись с задачей расчёта фундамента для своего дома я разложил его на множество «условно» отдельных балок, посчитал все возможные нагрузки и принялся за расчёты. Конечно, прежде всего я попытался разобраться в алгоритме расчёта и попытался посчитать всё вручную. Потом я нашёл несколько программок для расчёта жб балок и перепроверил свои расчёты. Не удовлетворившись данными этих программок, составил Exel-табличку, которая впоследствии переросла в программу калькулятор. Потом расчёты затянули меня на несколько месяцев в сопромат и программирование и как результат — вот довольно серьёзная программа расчёта ж/б балок.

С 12,01,2021 flash не поддерживается по умолчанию.
Вот способ от одного из подписчиков:
Шаг1. Удалить с компа все версии флэшплеера, у Adobe есть на сайте прога для этого.
Шаг 2. Скачать и установить флэшплеер версии 27 или ниже.

Метод работает в браузере Яндекс. Говорят, что ещё на Мозиле работает. Правда, в Хроме не работает всё равно.

После ввода любых числовых значений не забываем нажимать Enter, чтобы калькулятор их посчитал!

Основная идея расчёта сводится к тому, чтобы добиться баланса между прочностью бетона на сжатие и прочностью арматуры на растяжение. Иногда, в процессе расчётов каких-нибудь явно нереальных балок и нагрузок, можно увидеть, что калькулятор предлагает какое-то расчётное армирование, но при этом прочность балки не обеспечивается. Это следует понимать как то, что при таком сечении балки обеспечить прочность только арматурой невозможно. Т.е. калькулятор выдаёт сечение арматуры, при котором и бетон и арматура разрушатся одновременно и при этом наращивание армирования уже не приведёт к желаемому результату. Нужно либо уменьшать нагрузки/пролёты, либо увеличивать высоту/ширину сечения бетона.

1. Геометрические параметры балки

Некоторые программки, типа «Строитель+», расчитывают балку исходя из того, что известны длина пролёта, распределённая нагрузка на балку и марка бетона. В результате расчёта мы получим высоту, ширину и количество арматуры для обеспечения прочности балки. Это на начальном этапе не так и плохо, но зачастую геометрию нам диктуют условия строительства. Например, имея газобетонную стену шириной 290мм целесообразно сделать и балку перекрытия, скажем, над гаражными воротами шириной 290мм. Или, если вы хотите утеплить в последствии эту балку 5 см пенопласта, то нужно сделать ширину балки 240мм. Высоту тоже удобнее связать с высотой блока, ну или с 0,5 высоты блока, чтобы минимизировать отходы и работу по подрезке блоков. В случае балок внутри помещения зачастую у нас могут возникнуть ограничения по высоте балки. Например, проектируя гараж мы хотели получить выход на его крышу из «французского» окна второго этажа. При этом в гараже семиметровый пролёт, перекрываемый жб балкой — условие выхода из окна накладывало на высоту балки жёстке ограничение — не более 50см. Расчитывая ленту ростверка для фундамента по технологии ТИСЭ я так-же стремился сделать его по возможности ниже, чтобы на входе в дом было минимально возможное количество ступеней.

Итак, всеми этими примерами я хотел сказать то, что геометрические параметры зачастую нам заданы внешними факторами и порой требуется посчитать, сможем ли мы вложиться в отведённое нам пространство, а если не сможем, то сколько нужно арматуры, чтобы это стало возможным. Конечно, для того, чтобы с чего-то начать подбор сечения в случае расчёта с нуля, неплохо было бы иметь какую-то отправную точку. Для этого нам нужно знать хотя бы два параметра: длину балки и нагрузку на балку. Двух этих параметров программе будет достаточно, чтобы предположить минимально возможные высоту и ширину балки (в столбике с расчётами мелким курсивом).

Пример из моей стройки. Я, не зная ещё ничего о форме своей ленты-ростверка на столбах ТИСЭ, размышлял следующим образом. Диаметр столбов ТИСЭ у меня 200мм. В процессе их заливки я местами немного ошибался, то они на пару миллиметров толще, то уже, то при бурении бур увело в сторону на 5мм, то ветер сдувал разметочную верёвочку и т.п. В общем, я принял ширину ленты 220мм (200мм — столб + 20мм запас). Далее, высота балки обычно принимается как b / 0.3 ÷ 0.5, т.е. высота лежит в диапазоне 440 ÷ 730 мм. Нагрузки от каркасного дома у меня не большие, максимум 2500кг/м.п., а максимальный пролёт между столбами равен 2800мм в свету (ограничен несущей способностью грунта и диаметром расширения столба ТИСЭ). Потому рассчитываю балку сечением 440 х 220. При таких вводных данных получается, что для армирования достаточно 2 прута диаметром 10мм в одном ряду и процент армирования лежит ниже рекомендованного порога в 0,3%. Это не плохо, но экономически необосновано — нужно слишком много бетона! Поскольку ширину балки уменьшать некуда, уменьшаем высоту. Минимально рекомендованная 250мм, округляю её до целого числа 300мм (опалубку легче делать из двух досок 150мм). Считаем. Армирования достаточно 3 х 12мм и процент армирования в оптимальных пределах. Высота в 300мм меня устраивает по эргономическим соображениям, а расход бетона снижен на 32%. Ещё парочка расчётов со значениями высоты 250мм и 350мм показала, что 250мм требует уже большего расхода арматуры, и цена за арматуру начинает перевешивать экономию на бетоне, а 350мм вроде и не плохо, но усложняется конструкция опалубки и нужно «лишних» 2 куба бетона. Конечно, я не упомянул о классе бетона! Но, у нас в городе разница за куб бетона В20 и В30 не такая уж и большая, и я выбирал всегда бетон класса В30. Известны случаи, когда реальный класс бетона несколько не соответствует заказываемому, поэтому я предпочёл заказывать бетон более высокого класса в расчёте на то, что он, вероятно, на самом деле В25, а то и вовсе В20.

2. Определение опор балки

С точки зрения сопромата, будет ли это перемычка над дверным или оконным проемом или балка перекрытия, значения не имеет. А вот то как именно балка будет опираться на стены имеет большое значение. С точки зрения строительной физики любую реальную опору можно рассматривать или как шарнирную опору, вокруг которой балка может условно свободно вращаться или как жесткую опору. Определить расчётную схему не сложно:

Балка на шарнирных опорах. Если железобетонная балка устанавливается в проектное положение после изготовления, ширина опирания балки на стены меньше 200 мм, при этом соотношение длины балки к ширине опирания больше 15/1 и в конструкции балки не предусмотрены закладные детали для жесткого соединения с другими элементами конструкции, то такая железобетонная балка однозначно должна рассматриваться как балка на шарнирных опорах. Это наиболее вероятная схема в частном домостроении.
Защемлённая на концах балка. Если железобетонная балка изготавливается непосредственно в месте установки, то такую балку можно рассматривать, как защемленную на концах только в том случае, если и балка и стены, на которые балка опирается, бетонируются одновременно или при бетонировании балки предусмотрены закладные детали для жесткого соединения с другими элементами конструкции. Во всех остальных случаях балка рассматривается, как лежащая на двух шарнирных опорах.
Консольная балка. Балка, один или два конца которой не имеют опор, а опоры находятся на некотором расстоянии от концов балки, называется консольной. Например плиту перекрытия над фундаментом, выступающую за пределы фундамента на несколько сантиметров, можно рассматривать как консольную балку.
Многопролетная балка. Иногда возникает необходимость рассчитать железобетонную балку перекрытия, которая будет перекрывать сразу две или даже три комнаты, монолитное железобетонное перекрытие по нескольким балкам перекрытия или перемычку над несколькими смежными проемами в стене. В таких случаях балка рассматривается как многопролетная на шарнирных опорах. Это уже значительно более сложная в расчёте конструкция. Её, конечно, можно рассматривать как отдельные шарнирно опёртые балки, но это совсем не так! При равных по длине пролётах самый большой изгибающий момент образуется не в пролётах, а над опорами и в этом случае особое значение приобретает рассчёт арматуры именно верхнего ряда. Мой калькулятор пока умеет рассчитывать лишь двухпролётные балки.

Лента-ростверк в фундаменте ТИСЭ однозначно относится к Многопролётным балкам, однако, я её рассчитывал, как набор несвязанных между собой шарнирно опёртых балок, нагруженных равномерной нагрузкой от стен дома. В реальности, конечно, все сегменты ленты армированы максимально длинными кусками арматуры (12 метров), соблюдая все правила армирования по расположению стыков, нахлёстов, примыканий, длин анкеровки и установке поперечных хомутов. Что даёт мне значительный запас по прочности в условиях очень «ажурного» сечения балки. Такую конструкцию целесообразнее расчитывать в два прохода: все центральные элементы — это балки с двумя защемлёнными концами, а пролёты возле углов и Т-образные примыкающие пролёты — по схеме с одним защемлённым и одним шарнирно-опираемым концами. Чем больше пролётов в балке, тем ближе она будет к подобному упрощению (начиная с 5 пролётов — разбежка ).

3. Определение нагрузки на балку

Нагрузки бывают распределёнными и сосредоточенными. В жизни, конечно, всё сложнее: распределённые нагрузки могут быть равномерно и неравномерно изменяющимися, сосредоточенные нагрузки почти всегда сопровождаются некоторыми распределёнными, а ещё все эти сочетания могут быть статическими или динамическими, или обоими одновременно! С одной стороны конструкцию следует рассчитывать на максимально неблагоприятное сочетание нагрузок, с другой стороны теория вероятности говорит о том, что вероятность такого сочетания нагрузок крайне мала и рассчитывать конструкцию на максимально неблагоприятное сочетание нагрузок, значит неэффективно тратить строительные материалы и людские ресурсы. Поэтому при расчете конструкций динамические нагрузки используются с различными поправочными коэффициентами, учитывающими вероятность сочетания нагрузок, но как показывает практика, учесть все невозможно. Для примера я покажу вам свои расчёты нагрузки на ленту-ростверк:

Как видите, динамическая нагрузка вносит очень ощутимый вклад в суммарное значение всех нагрузок, хотя она вряд ли когда-нибудь случится. Для дальнейших расчётов я округлил нагрузку в 2242кг*м.п. до 2500кг*м.п., Вдруг я на старости лет увлекусь роялем и бильярдом одновременно =)

К этой же нагрузке стоит добавить ещё и нагрузку от собственного веса балки. При размерах 0,22 х 0,3 х 3 метров объём балки составит 0,198 м³, что при плотности железобетона 2500кг на кубометр составит 495кг. В калькуляторе эти величины так-же вычисляются, и автоматически добавляются к полезной нагрузке, если стоит галочка напротив строчки «Добавлять вес балки?»

Поскольку стены дома конструктивно обшиты ОСП-плитами, равномерно распределяющими нагрузку от стоек каркаса по всему обвязочному брусу я принимаю нагрузку, как равномерно распределённую.

4. Класс арматуры

В последнее время я несколько раз уже покупал арматуру, и ни разу не видел арматуру диаметров 10 — 16мм другого класса, кроме как А500С. Это самая подходящая арматура, рекомендованная современными правилами. Тем не менее, в программу-калькулятор я включил почти всю линейку современных классов арматуры (от А240 до А1000) и те классы, которые были в старых сводах правил (типа А-I, A-II, A-III). Мало ли, кто где какую арматуру раздобудет. Для расчётов и на практике я использовал арматуру класса А500С диаметром 12мм.

5. Армирование

Этот пункт в калькуляторе находится в разделе исходных данных, однако имеет некоторую «обратную связь» от расчётов. Задавая количество прутов арматуры в растянутой зоне балки программа рассчитает требуемый диаметр этих прутов и если выбранный диаметр меньше расчётного, покажет это. Как выбрать количество прутов? Для этого в раздлах СНиП есть ряд правил, которые я описал в статье «правила армирования». В общем случае, если это не узенькая слабонагруженная перемычка над окном, рекомендуется не менее двух прутов. Есть ограничения и на максимальное количество прутов, обусловленное расстоянием между прутами. Это минимальное расстояние определено необходимостью свободного протекания бетонной смеси в тело ленты между стержнями арматуры фундамента при заливке бетона, возможностью его уплотнения и хорошей связи бетона с арматурой для совместной работы под нагрузкой. Минимальное расстояние между стержнями продольной арматуры не может быть меньше наибольшего диаметра стержней арматуры и не менее 25 мм для нижнего ряда арматуры и 30 мм — для арматуры верхнего ряда при двух рядах армирования. Таким образом, максимальное количество прутов:

N=b-2a/(D+25)

округлённое до меньшего целого. В моём примере ширина балки b=220мм, толщина защитного слоя a=35мм (задана пластиковыми фиксаторами арматуры типа «звёздочка»), диаметр арматуры D=12мм:

N=220-2*35/(12+25)=4

С целью уменьшения арматурных работ я выбрал 3 прута. До расчётов диаметра мы еще дойдём.

6. Максимально допустимый относительный прогиб

Все строительные, и не строительные тоже, конструкции прогибаются! Не бывает таких материалов, которые не гнутся совсем. Железобетон не исключение, он может прогибаться под нагрузками в некоторых пределах без разрушительных последствий, причём порой на достаточно большие величины. СНиП 2.01.07-85 «Нагрузки и воздействия» регламентирует максимально допустимые прогибы, причем часть из этих ограничений связаны не с конструктивными проблемами бетонных балок, а просто с эстетическими (некрасиво, если плита перекрытия над головой прогибается на 10см, не смотря на то, что прочность обеспечена!) Выбираем требуемый в конкретном случае прогиб. В моём примере выбран прогиб 1/200, что означает, что при пролёте 3 м максимальный прогиб может составить 15 мм.

7. Изгибающий момент (начало расчётов)

Определение изгибающего момента — ключевое действие в расчёте. Все последующие вычисления будут опираться на эту величину. К сожалению, существует очень много самых разнообразных случаев приложения нагрузки к балке, да и балки бывают на разных опорах, да ещё и балки бывают статически определимые и неопределимые. Потому нету одной универсальной формулы, по которой можно вычислить изгибающий момент в любой ситуации (возможно, математики скажут, что я не прав, но двойные интегралы в уравнениях общего вида лежат за гранью моего понимания). Для определения наиболее подходящей для каждого конкретного случая формулы я порекомендую вот этот сайт, формулами которого я пользовался для написания своего калькулятора. В моём примере с равномерно распределённой нагрузкой (2500кг/м + собственный вес балки 495 кг / 3 м = 2665 кг/м) и шарнирно опёртой балкой изгибающий момент считается по формуле:

М=ql²/8

М=2665 х 3²/8=2998 кгс*м

Если бы нагрузка была сосредоточенной посередине балки, то: М=Ql/4.

8. Высота сжатой зоны

Следующим важным шагом является определение высоты сжатой зоны бетона и сравнение её с граничным условием.

Железобетон — это композитный материал, прочностные свойства которого зависят от множества факторов, точно учесть которые при расчете достаточно сложно. Кроме того бетон хорошо работает на сжатие, а арматура хорошо работает на растяжение, а при сжатии возможно вспучивание арматуры. Поэтому конструирование железобетонной конструкции сводится к определению сжатых и растянутых зон. В растянутых зонах устанавливается арматура. При этом высота сжатой и растянутой зоны зараннее неизвестна и потому применять обычные методы подбора сечения, как для деревянной или металлической балки, не получится.

Для начала определяем граничную высоту сжатой зоны. Это такая высота бетона, при которой его предельное напряжение на сжатие наступает одновременно с предельным напряжением в арматуре на растяжение. Т.е. при такой высоте сжатой зоны будет достигнут баланс между двумя разнонаправленными силами, сжатием и растяжением, и при превышении нагрузки произойдет одновременное разрушение бетона и обрыв арматуры. Граничная высота считается по следующей формуле:

ξr= ω/(1+Rs/Rpr*(1- ω/1,1))

где ω — характеристика сжатой зоны бетона, определяемая по формуле:

ω = k — 0,008 · Rb

где в свою очередь k — коэффициент, принимаемый равным для бетона: тяжёлого — 0,85; мелкозернистого — 0,80;

Rb — сопротивление бетона класса В25 сжатию: 14.5 МПа.

Итого: ω = 0,85 — 0,008 · 14,5 = 0,734.

Rpr — предельное напряжение в арматуре сжатой зоны сечения, принимаемое равным 500 Н / мм²

Rs — сопротивление арматуры класса А500 растяжению, 435 МПа.

ξr=0,734/(1+435/500*(1-0,734/1,1))=0,57

Поскольку это относительная высота, её можно перевести в абсолютную: ξr*h=171мм.

Высота сжатой зоны бетона c учётом сжатых стержней арматуры:

x=(RsAs-RscAsc)/(Rb*b)

где As — площадь сечений растянутой арматуры, в нашем примере 3 прута по 12мм, Asc — площадь сжатой арматуры (2 прута 10мм):

As=пR²*N;

As=3,14*0,6²*3=3,39 см² Asc=3,14*0,5²*2=1,57 см²

x=(435*3,39-400*1,57)/(14,5*22)=2,66 см

9. Коэффициенты Аm и Ar

Расчёт требуемой площади арматуры можно вести по алгоритму, изображённому ниже:

Для расчёта необходимого сечения арматуры нужно вычислить коэффициент Аm.

Аm=М/(Rb*h0²*b)

Поскольку М у нас в кг*м, Rb в Мпа, а величины b и h0 в см нужно всё привести к единым размерностям. М=2998 кг*м=299800 кг*см, Rb=14.5 МПа=147,86 кг/см² , теперь можно считать:

Am=299800/(147,86*26,5²*22)=0,131

Если значение Am будет больше Ar, то потребуется увеличить сечение бетонной балки, или повысить класс бетона. Если же таких возможностей или желаний нет, то необходимо устанавливать арматуру в сжатой зоне бетона!

Коэффициент Ar вычисляется по формуле:

Ar=ξr(1-0,5ξr)

Ar=0,57(1-0,5*0,57)=0,408

Условие Am<Ar у нас выполняется, значит сжатой арматуры добавлять не требуется.

10. Площадь растянутой арматуры

Расчёт необходимой площади сечения растянутой арматуры ведётся по формуле:

Fa=M/(Rs*h0*η)

где η = 0,5*(1+√(1-2*Am)) = 0,5*(1+√0,738) = 0,93

Поскольку у нас в расчёте опять размерности не совпадают, приведём все данные к единой системе, для удобства — к сантиметрам.

Rb=14.5 МПа=147,86 кг/см², Rs=435 МПа=4435,76 кг/см² .

Fa=299800/(4435,76*26,5*0,93)=2,74 см²

Поскольку количество стержней мы уже предварительно выбрали (N=3), то площадь сечения одного стержня должна быть не менее Fa/N = 2,74 / 3 = 0,914 см². Несложно посчитать диаметр этого стержня:

D=√(S/π)*20 D=10,79 мм

Округляем до ближайшего большего значения из номенклатурного ряда — 12мм. Итого, получается для армирования балки из моего примера достаточно 3 прута арматуры диаметром 12мм.

11. Проверка

Поскольку площадь растянутой арматуры отличается от расчётной, можно провести обратный расчёт для того, чтобы узнать, насколько большой у нас получился запас прочности. Сначала вновь пересчитываем площадь арматуры:

As=N*π*(D/2)² = 3,39 см²

Затем считаем максимальный изгибающий момент. Если условие Am<Ar выполняется и высота сжатой зоны х>0, то используется формула:

Mmax=Rb*b*х*(h0-0.5*х)+Rsс*Asс*(h0-a)

Mmax=147,86*22*2,66*(26,5-0,5*2,66)+4078,86*1,57*(26,5-3,5) =365078 кг*см (3650,7 кг*м = 35,8 кН*м)

где a — толщина защитного слоя бетона 3,5 см, Rsc — Предел прочности арматуры на сжатие Rsc=400 МПа=4078,86 кг/см²

Если х меньше или равен нулю, то используется другая формула: Mmax=Rs*As*(h0-а)

А если не выполняется условие Am<Ar, то: Mmax=Ar*Rb*b*h0²+Rsс*Asс*(h0-a)

Для того, чтобы перевести это значение в распределённую нагрузку, воспользуемся формулой из пункта 7:

q=8M/l²

q=8*3650,7/3²=3245 кг*м

Поскольку наша расчётная нагрузка составляет 2665 кг*м (с учётом собственного веса), то получается запас по прочности 21%.

12. Процент армирования

Процент армирования балки, это не самая критически важная величина в расчёте, потому я её оставил на последнем месте. Считается эта величина по формуле:

μ = (Fa+Fa’)/b*h0*100

μ=(3,39+1,57)/(22*26,5)*100=0,85%

Существуют рекомендованные диапазоны процента армирования балок от 0,3 до 4% (для колонн до 5%), выведенные изходя из экономических и конструктивных соображений, и наш результат отлично вписывается в этот диапазон.

13. Прогиб

Нередко бывает так, что прочность балки по первой группе предельных состояний достаточна, а вот расчёт по второй группе выходит за пределы допустимых деформаций. Потому расчёт на прогиб мне показался достаточно необходимым, чтобы потратить своё время и включить его в калькулятор. Приводимый ниже расчет не совсем соответствует рекомендациям СНиП 2.03.01-84 и СП 52-101-2003, тем не менее позволяет приблизительно определить значение прогиба по упрощенной методике. И хотя шарнирно опертая безконсольная однопролетная балка c прямоугольной формой поперечного сечения, на которую действует равномерно распределенная нагрузка — это частный случай на фоне множества возможных видов нагрузок, расчетных схем и геометрических форм сечения, тем не менее это очень распространенный частный случай в малоэтажном строительстве.

Прогиб балки для моего примера считается по формуле:

f = k5qlᶣ/384EIp

Эта формула очень похожа на класическую формулу прогибов, как в расчётах деревянных элементов и отличается наличием коэффициента k. Этот коэффициент учитывает изменение высоты сжатой области сечения по длине балки при действии изгибающего момента. При равномерно распределенной нагрузке и работе бетона в области упругих деформаций значение коэффициента для приближенных расчетов можно принимать k = 0.86. Использование этого коэффициента позволяет определять прогиб балки (плиты) переменного сечения, как для балки постоянного сечения с высотой hmin. Таким образом в приведенной формуле остается только 2 неизвестных величины — расчетное значение модуля упругости бетона и момент инерции приведенного сечения Ip в том месте, где высота сечения минимальна. Остается только определить этот самый момент инерции, а модуль упругости примем равный начальному. Момент инерции приведённого сечения Ip вычисляется довольно сложным и запутанным методом, в процессе которого необходимо решать кубическое уравнение, поэтому, если очень хочется вникнуть в суть и пересчитать всё самому, отправлю вас на сайт, где этот метод описан по шагам с картинками, чтобы совсем уж не копировать сайт автора )

Момент инерции балки J и момент сопротивления W калькулятор расчитывает по методике, описанной на указанном сайте и выдаёт результат в двух первых строчках правого столбца с расчётами.

14. Прочность по наклонным сечениям

Этим расчётом никогда нельзя пренебрегать, поскольку бетон не переносит

растягивающих усилий, а возле опор, на которые опирается балка, создаются

именно такие усилия, которые к тому-же не скомпенсированы никакой арматурой

(если не ставить хомуты). Если расчёт по прогибу и по прочности проходит, то это

совсем не означает, что балка не разрушится возле опоры из-за наклонной трещины.

Суть возникновения этой трещины изображена на картинке справа.

Для начала нам нужно определить реакции опор.

Поскольку мы рассматриваем нашу балку как шарнирно опёртую, то реакции левой и правой опор будут равны между собой, т.е. нагрузка между ними распределиться поровну.

Qопоры = q*L*0,5 = 2665 * 3 * 0,5 = 3998 кг = 39,2 кН (4т на каждую опору)

Прочность балки по наклонным сечениям обеспечивается прочностью бетона и поперечной арматуры, расположенной в теле балки.

Выясняем необходимость постановки поперечного армирования по расчету из условия:

Qопоры ≤ Qmin

где Qmin — расчетная поперечная сила, воспринимаемая железобетонным элементом без поперечной арматуры.

Расчетную поперечную силу Qmin, воспринимаемую элементом без вертикальной и (или) наклонной арматуры, допускается определять по формуле (7.78a) п.п. 7.2.1.6 СНБ 5.03.01-02 :

Qmin = ϕс * Rbt * b * ho

где коэффициент ϕс принимается равным:

для тяжелого бетона — 0,6;
для мелкозернистого — 0,5.

Rbt — сопротивление бетона растяжению Rbt=1,05 МПа=1050 кПа, а b и h0 выражены в миллиметрах.

Qmin = 0,6 * 1,05 * 220 * 265 = 36729 H = 36,7 кН

Поскольку Qопоры (39,2 кН) > Qmin (36,7 кН), бетон возле опоры не выдерживает нагрузки и требуется расчёт поперечного армирования.

15. Поперечное армирование

Диаметр хомутов в вязанных каркасах должен быть не менее 5 мм при h ≤ 800 мм и 8 мм при h > 800 мм. Высота нашего сечения 300 мм, но для хомутов у нас запасена арматура диаметром 6мм. Хомуты представляют из себя изогнутую рамочку, обхватывающую продольную арматуру, а значит площадь сечения хомута является удвоенной площадью сечения арматуры диаметром 6мм:

Asw = 3,14*0,3²*2 = 0,5652 см².

Максимально допустимый расчётный шаг хомутов определяем по формуле (Пособие по проектированию жбк, к СНиП 2.03.01-84 п.п. 3.29 (46)):

Smax = ϕb4 * Rbt * b * ho²/Q

Smax = 1,5 * 1050 кПа * 0,22 м * 0,265² м / 39,2 кН = 0,62 м

где фb4 | фb3 | фb2:

— для тяжёлого бетона: 1,5 | 0,6 | 2,00

— для мелкозернистого и лёгкого плотностью выше D 1900: 1,2 | 0,5 | 1,7

— для лёгкого D < 1900 и пористого: 1,0 | 0,4 | 1,5

Однако, согласно СНБ 5.03.01-02 п.п. 11.2.21, в железобетонных элементах, в которых поперечная сила не может быть воспринята только бетоном, поперечную арматуру следует устанавливать с выполнением следующих конструктивных требований, определяющих шаг поперечных стержней:

— при h ≤ 450 мм — не более h/2 и 150 мм;
— при h > 450 мм — не более h/3 и 300 мм;

— не более 3/4h и 500 мм;

Таким образом, в средней части пролета шаг поперечных стержней принимаем S = 3/4*30 = 22 см, (что не превышает 3/4h = 3/4*30 = 22,5 см). Исходя из равномерного распределения по длине центральной части у меня получилось 25 см, что, в принципе, допустимо в виду незначительного превышения Qопоры над Qmin.

В приопорных участках шаг поперечных стержней не должен превышать 15 см и не более h/2 = 30/2 = 15 см. Принимаем 15 см.

Вычисляем интенсивность усилий в поперечных стержнях на единицу длины балки:

qs = Rsw * Asw / S

qs = 290 000 кПа * 0,00005652 м² / 0,15 м = 109,27 кН/м

где Rsw — сопротивление растянутой поперечной арматуры класса АIII = 290 МПа;

Asw — площадь сечения арматуры хомута;

S — расстояние между хомутами в этой проекции, S = 15 cм.

Минимальная интенсивность:

qsmin = фb3 * Rbt * b / 2

qsmin = 0,6 * 1050 * 0,22 /2 = 69,3 кН/м

Требуемая интенсивность:

qsтр = Q² / (4 * Mb)

где Mb = фb2 * Rbt * b * ho²

Mb = 2 * 1050 * 0,22 * 0,265² = 32,44 кН·м

qsтр = 39,2² / (4 * 32,44) = 11,84 кН/м

Так как принятая интенсивность (109 кН/м) больше требуемой (11,84 кН/м) и больше минимальной (69,3 кН/м), оставляем шаг S = 15 см.

16. Ширина приопорных участков

Ширину приопорных участков вычислим по длине проекции опасной наклонной трещины на продольную ось балки:

с0 = √(Mb/qs) = √(32,44 / 109,27) = 0,55 м

Учитывая границы с0 в расчёте (ho < c0 < 2ho), принимаем с0 = 53 см. Несущую способность наклонного сечения проверяем по условию:

Qmax = Mb / c0 + qs * c0 = 32,44 / 0,55 + 109,27 * 0,55 = 119 кН

Qmax (119 кН) > Qопоры (39,2 кН)

Условие выполняется! Такой запас несущей способности у нас образовался благодаря хомутам диаметром 6 мм. Для данного случая можно было использовать хомуты диаметром 5мм, которые даже в приопорных учасках можно было бы ставить на расстоянии, как и в средней части пролёта — 25 см, но требования СНБ написаны не просто так!

P.S.: Если у вас балка планируется неразрезная многопролётная и с более-менее равными пролётами (+/-10%), и вы её надеетесь посчитать самостоятельно, то вам может пригодиться график эпюр изгибающих моментов. Для совсем ручного счёта рекомендую пролистать статейку про монолитное реблисто-балочное перекрытие.

__________________________________________________________________________________________________________________________________________________________________

Более подробные инструкции по расчёту бетонных и железобетонных изделий можно получить в «Пособии по проектированию бетонных и ж/б конструкций», и в СНБ 5.03.01-02. В документе изложено очень много информации по железобетону и так-же множество примеров расчётов.

Бесплатный онлайн-калькулятор луча | Civils.ai

Создание диаграмм изгибающих моментов, диаграмм поперечной силы и измерение прогиба для неопределенного пролета балки.

Рассчитайте изгибающий момент, поперечную силу, силы реакции и прогиб, используя свойства реального стального сечения.

Этот инструмент оптимизирован для настольного использования

Длина балки: 10,0 м
Второй момент площади: 473,0 см ⁴
Модуль Юнга: 210,0 ГПа

Загрузка. ..

Условия поддержки неудовлетворительны, добавьте другую поддержку.

Загрузка…

Макс. БМ: Мин. BM:

Макс. SF: Мин. SF:

Макс. отклонение:
Мин. отклонение:

Как работает этот анализ?

Введение

Балки бывают самых разных форм и размеров, понимание того, как рассчитать силы, действующие на конструкционную балку, может быть затруднено. Но здесь мы дадим вам краткое введение в теорию того, как они устроены. Начиная с теории напряжение балки .

Что такое напряжение балки и как рассчитать напряжение балки?
Когда мы прикладываем силу где-то вдоль пролета балки, мы создаем внутренние напряжения. Существует два типа напряжений, которые создаются:
Нормальное напряжение: Возникает из-за сил, действующих по длине балки при сжатии или растяжении.
Напряжение сдвига: Возникает из-за сил, действующих параллельно направлению нагрузки.
Происхождение этих двух компонентов напряжения можно разделить на два компонента силы, которые мы называем Изгибающий момент и Сила сдвига .
Типы внешней нагрузки
Простейшие нагрузки, прикладываемые к балке, можно разделить на три категории:
Точечные нагрузки: Это сила, приложенная к одной точке балки.
Распределенные нагрузки: Эта сила распределяется по определенной длине и действует как форма давления.
Сосредоточенный момент: Это чистый момент, действующий на балку в заданном положении.
Типы опор
Простейшие опоры для балки можно разделить на три категории:
Штифтовая опора: Удерживает балку как в горизонтальном, так и в вертикальном направлениях, не ограничивая ее вращение.
Роликовая опора: Опора балки только в одном направлении, без ограничения изгиба или вращения.
Фиксированная опора: Эти опоры обеспечивают фиксацию балки во всех направлениях и препятствуют вращению.
Диаграмма сил свободного тела
Чтобы найти силы, действующие на балку, мы должны следовать процессу создания диаграммы сил свободного тела.
Как рассчитать силы реакции опор на пролет балки?
Сначала мы рисуем балку в масштабе с указанием силовых составляющих приложенных нагрузок, а затем рассчитываем силы реакции опоры.
Для расчета реакций необходимо использовать уравнения равновесия для разрешения внешних сил:
Σ Приложенные вертикальные силы = 0 кН
Σ Приложенные горизонтальные силы = 0 кН
Σ Прикладываемые моменты = 0 кНм
Существует два типа случаев при разрешении внешних условий балки:
Статически определяемые: Где количество уравнений равно количеству неизвестных, и расчеты могут быть решены с помощью ручных вычислений в закрытой форме.
Статически неопределимое: Когда количество неизвестных превышает количество уравнений и необходимо использовать более продвинутые методы, такие как теория сопротивления момента.
Как нарисовать диаграмму поперечной силы?
Чтобы создать диаграмму поперечной силы, вы работаете слева направо поперек балки, суммируя приложенные силы и реакции в каждой точке приложения. Консоли являются наиболее простым примером этого с единственной реакцией на одном конце пролета балки с нулевой силой сдвига на неподдерживаемом конце.
Как нарисовать диаграмму изгибающего момента?
Чтобы создать диаграмму изгибающего момента, вы снова должны работать слева направо поперек балки и вычислять момент слева от каждой интересующей вас точки. наш расчет стальной балки для расчета в соответствии с Еврокодом 3.
Проектировщик стальных профилей
Расчет бетонной балки
Результаты этого анализа затем можно использовать в нашем расчете бетонной балки для расчета в соответствии с Еврокодом 2.
Конструктор бетонных секций
Внесите свой вклад в этот код
Этот код является открытым исходным кодом, и вы можете внести свой вклад в его разработку.
Вы можете найти исходный код на GitHub здесь:
IndeterminateBeam
Специальные кредиты: Джесси Бонанно
Beam Calculator — PolyBeam прост и удобен в использовании!
Как начать работу с PolyBeam?
Чтобы начать работу с PolyBeam, выполните следующие действия:
Загрузите PolyBeam и запустите файл .exe.
Зарегистрируйтесь, указав свое имя и адрес электронной почты.
Для кого создан PolyBeam?
Калькулятор луча сделан инженерами для инженеров!
PolyBeam включает в себя проверку конструкции Еврокода, что делает его идеальным для инженеров-строителей, работающих в Европе.
Каковы некоторые из ключевых особенностей?
Простой в использовании калькулятор балок
Первое, что ассоциируется у наших пользователей с PolyBeam, — это простота. PolyBeam — это очень простой и интуитивно понятный калькулятор балок, что делает его очень простым в использовании, даже если вы не знакомы с ИТ и программным обеспечением. Опоры, нагрузки и свойства сечения вставляются с минимальным вмешательством пользователя. Одновременно PolyBeam нарисует графическое представление балки с приложенными нагрузками, рассчитает силы сечения и определит использование балки.
Боковая потеря устойчивости при кручении
Критический изгибающий момент от поперечной потери устойчивости при кручении определяется на основе энергетического метода, который учитывает высоту атаки нагрузки, силы сечения и ограничения. С помощью этого метода критический момент определяется с высокой точностью. Это часто приводит к более высокой несущей способности по сравнению с традиционными расчетами.
Упругие и пластические силы сечения
В отличие от традиционного инженерного программного обеспечения, PolyBeam определяет силы сечения как упруго, так и пластически. Это позволяет более широко использовать наиболее часто используемые стальные профили для статически неопределимых балок.
Расчетное предельное состояние (ULS)
Можно указать комбинацию нагрузки ULS. Если это будет сделано, PolyBeam проверит силы сечения из расчета балки с несущей способностью выбранного сечения и определит коэффициент использования. Дополнительные сведения о том, что входит в проверку проекта ULS, см. в вопросе «Что включает проверка проекта?».
Расчет предельного состояния пригодности к эксплуатации (SLS)
Можно указать два различных типа комбинаций нагрузки SLS: анализ собственной частоты или анализ прогиба. Анализ собственной частоты определяет первую собственную частоту луча и позволяет пользователю указать пороговое значение — это очень полезно при работе с требованиями к вибрации. аналогичным образом можно указать порог отклонения, так как по умолчанию используется L/400.
Противопожарное проектирование
Если указано сочетание пожарной нагрузки, PolyBeam рассчитывает температуру стали на основе продолжительности пожара и определяет несущую способность. Если секция не выдерживает нагрузки, можно найти критическую температуру стали и использовать ее для определения требуемой противопожарной изоляции.
Экспорт в PDF
Когда вы закончите расчет балки, очень легко задокументировать вашу работу. Просто нажмите на экспорт, выберите, какой контент вы хотите включить, и позвольте PolyBeam создать для вас короткий и элегантный PDF-документ. Эта функция является одной из самых популярных среди наших пользователей. См. пример.
Как работает PolyBeam?
Калькулятор балки PolyBeam разделяет балку на конечное количество элементов балки. Затем он использует метод конечных элементов для определения реакций и перемещений, из которых рассчитываются силы сечения. На их основе проверяется поперечное сечение по всей балке в соответствии с применяемыми требованиями ULS, SLS и противопожарного проектирования.
Какие материалы можно использовать?
В настоящее время доступны четыре варианта материала: PolyBeam: сталь, древесина, бетон и нестандартный материал.
Калькулятор стальных балок позволяет выбрать из наиболее часто используемых стальных профилей в Европе (IPE, HEA, HEB и HEM) или создать собственное сечение с помощью инструмента пользовательского сечения.
Калькулятор деревянных балок включает классы прочности как для клееной древесины, так и для массивной древесины. Это позволяет вам выбрать из стандартных деревянных секций или создать секцию с вашими собственными размерами.
Калькулятор бетонной балки включает возможность создания прямоугольной бетонной секции с продольной арматурой сверху и снизу. Способность к сдвигу может быть определена как для бетонных секций с поперечным армированием, так и без него.
Пользовательский материал позволяет указать жесткость материала (модуль Юнга и момент инерции), поведение материала (линейно-упругий или упруго-пластичный) и несущую способность. Несущая способность используется для проверки конструкции ULS и для определения момента текучести, если выбрано упругое идеально пластичное поведение материала.
Что включает в себя проверка дизайна?
Проверка стальных конструкций
Стальные профили могут быть рассчитаны на три типа проверок конструкции ULS, SLS и Fire.
Проверка конструкции ULS для стали включает изгибающий момент (EN 1993-1-1 6. 2.5), сдвиг (EN 1993-1-1 6.2.6), комбинированный изгиб и сдвиг (EN 1993-1-1 6.2.8) боковое выпучивание при кручении (EN 1993-1-1 6.3.2.4).
Проверка конструкции SLS включает анализ прогиба и анализ собственной частоты, где пороговые значения могут быть указаны пользователем.
Проверка противопожарной конструкции стали включает понижающие коэффициенты (EN 1993-1-2 3.2.1), изгибающий момент (EN 1993-1-2 4.2.3.3), поперечный крутящий момент (EN 1993-1-24.2.3.3) коробление (EN 1993-1-2 4.2.3.3).
Проверка конструкции деревянных конструкций
Деревянные секции могут быть спроектированы для ULS и SLS.
Проверка конструкции ULS для древесины включает в себя изгиб (EN 1995-1-1 6.1.6), сдвиг (EN 1995-1-1 6.1.7) и боковое изгибание при кручении (EN 1995-1-1 6.3.3).
Проверка конструкции SLS включает анализ прогиба и анализ собственной частоты.
Проверка конструкции бетона
Бетонные секции могут быть спроектированы для ULS и SLS.
Проверка конструкции бетона ULS включает изгибающий момент (EN 1992-1-1 6.1), способность к сдвигу как без арматуры на сдвиг, так и с ней (EN 1992-1-1 6.2.2 или EN 1992-1-1 6.2.2 соответственно) и вращательная способность (EN 1992-1-1 5.6.3)
Проверка конструкции SLS включает прогиб, ширину трещины, собственную частоту и ограничение напряжения. Пользователь может определить, следует ли включать ползучесть и усадку в расчет SLS.
Проверка конструкции по индивидуальному заказу
Материалы по индивидуальному заказу можно проверить как на изгибающий момент, так и на сдвиг, если пользователь определил соответствующие допустимые нагрузки на секции. Кроме того, можно проверить отклонение и собственную частоту.
Могу ли я получить скидку, если куплю несколько лицензий?
Да, если вы заинтересованы в нескольких лицензиях, свяжитесь с нами и сообщите нам, сколько лицензий вам нужно. Затем мы свяжемся с вами как можно скорее с цитатой.
Доступен ли PolyBeam за пределами Европы?
PolyBeam рассчитывает использование стальных профилей на основе проверки конструкции по Еврокоду. Кроме того, каталог стальных профилей в PolyBeam основан на стандартных европейских стальных профилях. В настоящее время мы не планируем включать другие коды дизайна, поэтому, если основная часть вашего бизнеса находится за пределами Европы, PolyBeam может быть не лучшим вариантом для вас.
Для получения дополнительной информации о калькуляторе балок PolyBeam свяжитесь с нами.
‎Beam Calculator lite в App Store
Описание
Калькулятор балок содержит 34 калькулятора для расчета и преобразования различных параметров балок и строительных конструкций. Доступны в имперских и метрических единицах измерения. Самый полный калькулятор луча.
*** Доступны в метрических и британских единицах измерения ***
• Критический изгибающий момент (прямоугольное поперечное сечение)
• Критический изгибающий момент (открытое поперечное сечение)
• Критический изгибающий момент (неравномерный градиент изгибающего момента)
• Коэффициент градиента момента
Дополнительные калькуляторы, доступные для покупки в приложении:
• Максимальное напряжение (осевая и изгибающая нагрузки)
• Максимальное напряжение (большой прогиб из-за изгиба)
• Прогиб (осевое сжатие и изгиб)
• Критическая нагрузка на изгиб
• Напряжение (несимметричный изгиб)
• Суммарное единичное напряжение (внецентренная нагрузка)
• Прогиб (внецентренная нагрузка)
• Напряжение (внецентренная нагрузка)
• Пробная расчетная площадь стали
• Площадь сжатия
• Глубина области сжатия
• Расстояние от центра тяжести до волокна с экстремальным сжатием
• Номинальный допустимый момент
• Скорректированная площадь стали
• Сбалансированный коэффициент армирования стали
• Минимальное армирование сталью Коэффициент
• Максимальный коэффициент армирования стали
• Требуемые размеры балки
• Прочность бетона на сдвиг
• Прочность стали на сдвиг
• Максимально допустимый сдвиг стали
• Максимально допустимый общий сдвиг
• Площадь горизонтального сдвига стали
• Угол стальной площади сдвига
• Расстояние между вертикальными хомутами
• Расстояние между угловыми хомутами
• Прочность на сдвиг вертикальных хомутов
• Прочность на сдвиг угловых хомутов
• Длина заделки хомутов
• Максимальное растяжение Steel Spacing
*** Доступно на английском, французском, испанском, итальянском, немецком и португальском языках ***
000Z» aria-label=»May 13, 2021″> 13 мая 2021 г.
Версия 5.1
— Быстрое исправление для решения проблемы с разблокировкой заблокированных калькуляторов в приложении.
Рейтинги и обзоры
8 оценок
Нет доступной информации
В App Store 7 лет и всего 1 отзыв? Давай, парень
Разработчик V PUGAZHENTHI указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные, используемые для отслеживания вас
Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям:
Расположение
Идентификаторы
Данные об использовании
Диагностика
Данные, связанные с вами
Следующие данные могут быть собраны и связаны с вашей личностью:
Расположение
Идентификаторы
Данные об использовании
Диагностика
Данные, не связанные с вами
Могут быть собраны следующие данные, но они не связаны с вашей личностью:
Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше
Информация
Продавец
В ПУГАЖЕНТИ
Размер
16 МБ
Категория
Утилиты
Возрастной рейтинг
4+
Авторское право
© Все права защищены
Цена
Бесплатно
Сайт разработчика
Тех. поддержка
Политика конфиденциальности
Еще от этого разработчика
Вам также может понравиться
Изгибающий момент: лучшие уравнения, которые нужно знать (бесплатный калькулятор)
В этой статье мы обсудим концепции, связанные с изгибающим моментом. Мы также предоставляем уравнения и калькуляторы для распространенных конфигураций балок.
Почему важен изгибающий момент?
Конструкция конструкций учитывает воздействие нагрузки. Поэтому для сохранения устойчивости конструкций решающее значение имеет сопротивление изгибающему моменту . Примерами нагрузок могут быть, например, динамическая нагрузка (люди или объекты в здании), статическая нагрузка (вес самой конструкции) и нагрузки от окружающей среды (снеговая нагрузка, ветровая нагрузка и землетрясения). Повреждение может произойти из-за изгиба, когда напряжение изгиба превышает предел прочности элемента.
Грузоподъемность в зависимости от спроса
Постоянные и временные нагрузки действуют на конструкции одновременно, изменяя взаимодействие всех их компонентов. В результате, проектируя структуру для обеспечения оптимальной устойчивости, инженеры должны учитывать и то, и другое. Способность балки выдерживать нагрузку — это вычисление, которое помогает определить общую прочность конструкции здания. Поскольку ни один материал не может выдержать бесконечную нагрузку, инженеры рассчитывают «изгибающий момент» с учетом внешних сил .
Внешние силы
Три силы влияют на расчетные параметры конструкции нагрузок:
Сжатие происходит, когда частицы вещества прижимаются друг к другу, укорачивая или сжимая их. Сжатие обычно применяется сверху конструкции. Узнайте больше о сжатии и его последствиях в этой статье: Потеря устойчивости колонны
Растяжение — это полная противоположность сжатия; при растяжении материал тянется силами тяги. Балка находится под растягивающей нагрузкой, когда балка выходит из строя в верхней части.
Сила скручивания, действующая на конструктивную часть, известна как кручение.
Вышеупомянутые три напряжения всегда присутствуют в конструкциях. Например, предположим, что вы прогуливаетесь по второму этажу дома. Затем ваш вес будет сжимать балки, поддерживающие пол. Следовательно, балки вверху сжимаются, а внизу растягиваются. Это создает изгибающий момент. Кроме того, срезное полотно удерживает балки вместе. В заключение, структура дома должна быть в состоянии сбалансировать все эти нагрузки, чтобы сохранить структурную целостность.
Что такое изгибающий момент?
Мера эффекта изгиба вследствие приложения поперечной силы к элементу конструкции известна как изгибающий момент. Таким образом, в проектировании конструкций изгибающий момент является важным элементом при проектировании конструкций. В противном случае было бы трудно понять поведение элементов конструкции при приложении поперечной нагрузки. Как упоминалось ранее, конструкция конструкции удерживает максимальные пределы изгиба конструкции в допустимых пределах. Однако при превышении пределов изгиба или сдвига конструкция не сможет сохранить свою устойчивость и в конечном итоге приведет к ее разрушению.
Изгибающие моменты, визуализированные на балке, подвергнутой двухосному изгибу.
Как рассчитывается изгибающий момент
Когда поперечная сила прикладывается к секции балки, возникающие напряжения называются напряжениями изгиба. Следовательно, приложенные силы вызывают изгибающий момент, который обычно измеряется как сила x расстояние (кН-м). При измерении изгиба сила должна быть перпендикулярна плечу момента . Балка является наиболее распространенным конструктивным элементом, подверженным изгибающим моментам, так как под нагрузкой она может изгибаться в любой точке по своей длине. Несмотря на различия в процессах, балка может разрушиться из-за касательных напряжений до разрушения изгиба. В этом случае изгибающая сила заставит балку вращаться вокруг точки поворота, если точка поворота не ограничена должным образом. Таким образом, точка, в которой возникает максимальный изгибающий момент, важна для расчета конструкции на изгиб.
Вывод уравнения изгибающего момента
Чтобы полностью понять контекст изгибающих моментов, мы должны изучить поперечное сечение балки при изгибе.
Дискретная полоса напряжения изгиба
Иллюстрация распределения напряжения по сечению при изгибе. Источник: Университет Аризоны
Из рисунка видно, что внутренние напряжения статически эквивалентны внешним силам и моментам. Во-первых, рассмотрим величину силы dF , действующую на полосу площадью дА . Развиваемое напряжение σ будет равно
Следовательно, момент M будет задан как
Здесь y — расстояние силы от нейтральной оси (т. на луче). Впоследствии, чтобы получить максимальное напряжение в крайней волокне, fb , мы можем использовать тригонометрический прием:
Напряжения изгибающего момента, возникающие в поперечном сечении.
Из подобия треугольников на рисунке выше мы можем получить
Преобразование приведенного выше уравнения
Где c — расстояние от нейтральной оси до вершины поперечного сечения, fbmax — максимальное напряжение на краю волокна, а σ — изгибные напряжения на полосе на расстоянии.
Интегрирование напряжения изгиба
Теперь мы можем подставить это в первое уравнение. Однако в начале вывода уравнения предполагалась одна полоса поперечного сечения. Чтобы включить все сечение, берется интегрирование;
Здесь мы определяем, что определение второго момента площади I можно использовать для упрощения уравнения.
Переставить для fbmax (Напряжение при изгибе)
Таким образом, напряжение fb на любом расстоянии, y от нейтральной оси будет
Мы также можем написать
Раздел
Y .
Допущения
Обратите внимание, что приведенный выше вывод уравнений изгибающего момента основан на следующих допущениях:
Во-первых, балка является линейной и имеет однородную площадь поперечного сечения до приложения напряжений.
Во-вторых, изгибающий момент возникает внутри продольной плоскости симметрии балки.
В-третьих, балка подвергается чистому изгибу (изгибающий момент не меняется по длине).
Наконец, материал, используемый в балке, является однородным и изотропным.
Вам понравился этот пост? Подпишитесь, и каждый месяц мы будем присылать вам еще больше таких замечательных постов.
Уравнения изгибающего момента
Разделы ниже содержат конфигурацию балки вместе с приложенной нагрузкой и формулами для расчета максимального изгибающего момента .
Консоли
В этом подразделе мы рассмотрим различные конфигурации нагрузки консольных балок.
Консоль – Точечная нагрузка на конце
Защемленная балка с вертикальной точечной нагрузкой на конце будет иметь максимальный момент на опоре. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.
Уравнение и диаграмма
Диаграмма изгибающего момента консоли – точечная нагрузка на конце
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой точечной нагрузке P в конце.
Консоль – равномерно распределенная нагрузка
Как и в приведенной выше конфигурации, защемленная балка с равномерно распределенной нагрузкой будет иметь максимальный момент на опоре. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.
Уравнение и диаграмма
Диаграмма изгибающего момента консоли – равномерно распределенная нагрузка
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой точечной равномерно распределенной нагрузке д .
Консоль – треугольная распределенная нагрузка
Как и в приведенной выше конфигурации, защемленная балка с треугольной распределенной нагрузкой будет иметь максимальный момент на опоре. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.
Уравнение и диаграмма
Диаграмма изгибающего момента консоли – треугольная распределенная нагрузка
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой точечной треугольной распределенной нагрузке д .
Консоль – конечный момент
Защемленная балка с моментной нагрузкой на конце будет иметь постоянный момент по всей балке. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.
Уравнение и диаграмма
Диаграмма изгибающего момента Консоль – конечный момент
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой мгновенной нагрузке M0 в конец.
Просто поддерживаемые балки
В этом подразделе мы рассмотрим различные конфигурации нагрузки свободно опертых балок. Другими словами, балки с одним концом на штифтах, а другой конец на ролике.
Просто поддерживаемая – промежуточная нагрузка
Теперь, если мы рассмотрим свободно опертые балки, общей конфигурацией является конфигурация с точечной нагрузкой на расстоянии a от первой опоры.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая – промежуточная нагрузка
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки общей длиной a + b , подверженной точечная нагрузка P расположен на расстоянии a от опоры.
Ф:
а:
б:
Простая опора – центральная нагрузка
Простая балка с точечной нагрузкой в центре. Максимальный момент возникает там, где приложена точечная нагрузка.
Уравнение и диаграмма
Диаграмма изгибающего момента Свободно опертая – нагрузка в центре
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подвергаемой точечной нагрузке P в центре.
Просто опертая – две точечные нагрузки на равном расстоянии от опор
Просто опертая балка с двумя точечными нагрузками на равном расстоянии от опор. Максимальный момент возникает между двумя точечными нагрузками.
Уравнение и диаграмма
Диаграмма изгибающего момента свободно опертой балки – двухточечные нагрузки на равном расстоянии от опор
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L две точечные нагрузки на равном расстоянии и от опор.
Просто опертая – равномерно распределенная нагрузка
Просто опертая балка с равномерно распределенной нагрузкой. Максимальный момент возникает в центре балки.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая – равномерно распределенная нагрузка
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной равномерно распределенной нагрузке нагрузка q .
Просто опертая – момент на каждой опоре
Просто опертая балка с двухточечной моментной нагрузкой на каждом конце. Момент постоянен по длине балки.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая – момент на каждой опоре
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной действию двух моментов нагрузки M0 на концах.
Просто опертая – момент на одной опоре
Просто опертая балка с моментной нагрузкой на одну опору. Диаграмма момента имеет треугольную форму, где максимальный момент возникает там, где приложен момент.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая – момент на одной опоре
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной одному моменту загрузите M0 с одного конца.
Свободно опертая, момент в средней точке
Свободно опертая балка с моментной нагрузкой, приложенной в центре. Максимальный момент будет в центре.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая, момент в средней точке
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной одному моменту нагрузки M0 в центре.
Заключение по изгибающему моменту
В заключение, изгибающий момент — это реакция, возникающая в элементе конструкции, когда на него действует внешняя сила или момент, вызывающий его изгиб. Балка является наиболее типичным или простейшим элементом конструкции, подверженным действию изгибающих моментов.
Чтобы проиллюстрировать это далее, рассмотрим момент (силу) на локте. Как упоминалось ранее в статье, момент прямо пропорционален плечу рычага. Точно так же он играет важную роль в определении параметров конструкции консольных конструкций. Если момент превышает расчетную прочность конструкции или любого другого компонента из-за чрезмерной нагрузки, она может разрушиться. Разрушение башен Всемирного торгового центра произошло из-за увеличения количества соединений, вызванных сильным жаром пожаров. При изменении моментов в конструкции передача усилий на другие элементы, соединения и узлы общей системы становится неуправляемой, что может привести к отказу.
Наконец, в настоящее время инженеры проектируют конструкции с помощью программного обеспечения для получения точных и быстрых результатов. Например, Tribby3d — облачное программное обеспечение для загрузки конструкций. Используя tribby3d, инженеры могут легко рассчитать площади притоков и нагрузку на элементы различных типов, таких как колонны и стены. Затем результаты можно экспортировать в различные выходные файлы, такие как Excel и AutoCAD.
Tribby3d — это облачное инженерное программное обеспечение, которое может вычислять загрузку элементов.
Связанные статьи
Бесплатный калькулятор балок — опорные реакции, изгибающий момент, поперечная сила
Бесплатный онлайн-калькулятор ASDIP для балок позволяет вам проектировать балки с опорой на шарнирах, неподвижно поддерживаемые и неразрезные балки с концевыми консолью. With this calculator you’ll be able to do the following:
Calculate Support Reactions
Generate Shear Force Diagrams
Generate Bending Moment Diagrams

Полная версия: расчет прогибов, расчет бетона, расчет стальных конструкций, подробные отчеты, прочность конструкции, расчет составных балок, пользовательские комбинации нагрузок, расписание балок и многое другое!
Пробная версия: То же, что и полная версия, но с небольшими ограничениями, такими как печать и сохранение. Позволяет протестировать все программное обеспечение ASDIP в течение 15 дней.
Начать бесплатную пробную версию
Стоимость полной версии
Нужно больше? Обновите до полной версии или подпишитесь на бесплатную пробную версию, чтобы разблокировать дополнительные функции луча.
ASDIP CONCRETE включает модули для проектирования неразрезных балок в соответствии с последним стандартом ACI 318-19. Вы можете смоделировать до пяти пролетов и двух концевых консолей с несколькими типами нагрузки, такими как равномерная, переменная, сосредоточенная и моментная. Программное обеспечение создает диаграммы сдвига и моментов, наложенные на диаграммы прочности конструкции. В расчеты включаются долговременные прогибы.
ASDIP STEEL включает модули для проектирования неразрезных балок, как составных, так и несоставных, в соответствии с последней версией AISC 360. Для составных балок программа рассчитывает необходимое количество срезных шпилек для частичного или полного составного действия. Программное обеспечение включает строительные нагрузки, а также конечные нагрузки в проекте. Комбинации нагрузок соответствуют ASCE 7-16 или определяются пользователем.
Начните бесплатную пробную версию и испытайте все, что может предложить ASDIP! Вы сможете оценить все программное обеспечение, включая модули балок, в течение 15 дней: включает пакеты для проектирования БЕТОН, СТАЛЬ, УДЕРЖАНИЕ и ФУНДАМЕНТ. Или разместить заказ и перейти на полную версию.
Начать бесплатную пробную версию
Стоимость полной версии
Как пользоваться калькулятором луча
Добро пожаловать в бесплатный онлайн-калькулятор луча ASDIP. Этот калькулятор балок позволяет моделировать до трех неразрезных пролетов и двух концевых консолей. Используйте вкладку Geometry , чтобы ввести размеры поперечного сечения балки, количество опор, длину пролета и тип опор, шарнирных или фиксированных. Типы балок могут быть прямоугольными, тавровыми, перемычками и L-образными балками.
Можно указать несколько различных типов нагрузки, например равномерные нагрузки, переменные нагрузки, сосредоточенные нагрузки и изгибающие моменты. Распределенные нагрузки могут быть приложены частично в любом пролете. Нажмите на вкладку Loads , чтобы ввести информацию о нагрузках на пролет. Выберите диапазон из раскрывающегося списка Segment . Нагрузки могут быть либо предварительно комбинированными нагрузками (без дополнительных коэффициентов нагрузки), либо набором номинальных загружений, которые должны быть объединены внутри. Комбинации нагрузок согласно ASCE 7-16. Собственный вес балки можно легко добавить к внешним нагрузкам.
Калькулятор реакций опор балки
Этот калькулятор балки может генерировать высоту балки, показывающую приложенные нагрузки на вкладке Graph . Программа рассчитывает опорные реакции для выбранного сочетания нагрузок. Затем эти силы реакции можно использовать для проектирования колонн и фундаментов. Обратите внимание, что в полной версии будут рассчитываться опорные реакции как для сервисных, так и для факторизованных комбинаций нагрузок.
Калькулятор диаграммы поперечной силы
Важной особенностью калькулятора балки является его способность генерировать диаграмму поперечной силы балки в Вкладка График для указанных нагрузок. Затем программа рассчитает поперечные силы вдоль балки для выбранного сочетания нагрузок. На диаграмме сдвига удобно показано максимальное усилие сдвига в критическом сечении в точке «d» от лица колонны. Обратите внимание, что полная версия также рассчитывает расчетную прочность на сдвиг вдоль балки и рисует эту диаграмму прочности на заднем плане для целей сравнения.
Калькулятор диаграммы изгибающего момента
Бесплатный инструмент расчета балки ASDIP также позволит вам создать диаграмму изгибающего момента балки для указанных нагрузок и для выбранной комбинации нагрузок в График табл. Чтобы увидеть диаграммы в большем масштабе для конкретного пролета, просто выберите его в раскрывающемся списке Segment . Обратите внимание, что полная версия также рассчитывает расчетную прочность на изгибающий момент вдоль балки и рисует эту диаграмму прочности на заднем плане для целей сравнения. Таким образом, если способность к изгибающему моменту в какой-либо точке превышает допустимую, это может быть немедленно определено.
Дополнительные бесплатные инструменты

Калькулятор опорной плиты
Калькулятор подпорной стены
Jonathan Ochshorn—Калькуляторы структурных элементов
Jonathan Ochshorn—Калькуляторы структурных элементовКалькуляторы структурных элементов
контакт
Jonathan Ochshorn
© 2013–2020 Jonathan Ochshorn.

Статика
Нагрузки
Натяжные элементы
Колонны
Балки
Соединения
Системы
0 90 Учебник БЕСПЛАТНО
0
9

Статика:
Калькулятор реакции свободно опертой балки: Расчет реакции для свободно опертой балки с равномерно распределенной нагрузкой и/или до 3 сосредоточенных нагрузок.
Калькулятор реакции трехшарнирной арки: Расчет реакции трехшарнирной арки при равномерно распределенной нагрузке и/или до 3 сосредоточенных нагрузок.
Калькулятор реакции кабеля: Расчет реакции кабеля с равномерно распределенной нагрузкой и/или до 3 сосредоточенных нагрузок.
Калькулятор момента и сдвига для свободно опертой балки: рассчитывает реакции, максимальные положительные и отрицательные изгибающие моменты, а также максимальные положительные и отрицательные внутренние поперечные силы для свободно опертой балки с равномерно распределенной нагрузкой и/или до 3 сосредоточенных нагрузок.
Калькулятор реакции фермы и силы стержня: Расчет реакции и силы стержня для ферм Howe, Pratt или Warren.
Калькулятор усилия стержня трехшарнирной арки: Расчет реакции и усилия стержня для «треугольных» трехшарнирных арок.
Калькулятор внутренней осевой силы троса: Расчет реакций и внутренних осевых сил троса.
Нагрузки:
Калькулятор постоянной и постоянной нагрузки: Расчет постоянной и постоянной нагрузки для балок, балок и колонн.
Калькулятор снеговой нагрузки: Расчет снеговой нагрузки на основе уклона, характеристик поверхности и других параметров.
Калькулятор определяющей нагрузки: Расчет сочетаний определяющей нагрузки для расчета допустимого напряжения или расчета прочности (LRFD). Более новая версия рассчитывает управляющие нагрузки на основе распределенных нагрузок на пол (psf), площадей притоков и количества этажей.
Калькулятор давления ветра: Вычисляет давление ветра (psf) на наветренную и подветренную стороны прямоугольных зданий с плоскими крышами после ввода значений скорости ветра, экспозиции, высоты крыши, важности, размеров в плане, коэффициента направленности и коэффициента топографии.
Калькулятор сейсмической и ветровой нагрузки: Расчет и сравнение ветровой и сейсмической нагрузки на здание после ввода общих данных (город, фактор важности), сейсмических данных (класс площадки, система сопротивления сейсмической силе) и данных о ветре (категория воздействия). , размеры в плане и парапете, а также коэффициенты направленности и топографии).
Натяжные элементы:
Удлинение под действием осевой нагрузки Калькулятор: Рассчитывает удлинение (а также напряжение и деформацию) для призматических элементов, подверженных осевой нагрузке.
Нагрузочная способность деревянного натяжного элемента Калькулятор: Рассчитывает нагрузочную способность деревянного натяжного элемента на основе допустимого натяжения на площади сетки (уменьшенной на отверстия под болты) и, при необходимости, на отрыв рядов и групп.
Калькулятор несущей способности стального натяжного элемента: Расчет несущей способности стального натяжного элемента на основе текучести общей площади или разрыва эффективной полезной площади.
Колонны:
Калькулятор деревянных колонн: рассчитывает грузоподъемность (максимальную безопасную нагрузку) для деревянных колонн после ввода значений модуля упругости, допустимого напряжения, продолжительности коэффициента нагрузки и эффективной длины (высоты).
Калькулятор стальных колонн: рассчитывает грузоподъемность (максимальную безопасную нагрузку) для стальных колонн после ввода значений для обозначения ASTM, типа сечения, коэффициента эффективной длины и длины без связей.
Калькулятор конструкции W-образной стальной колонны: Находит самую легкую W-образную стальную колонну для заданной осевой нагрузки и эффективной длины. (старая версия)
Калькулятор железобетонных колонн: Анализ и расчет связанных или спиральных (прямоугольных или круглых) железобетонных колонн на основе метода прочности.
Балки:
Калькулятор деревянных балок: выбирает самые легкие пиломатериалы после ввода значений пролета, шага, породы, класса, критериев прогиба и критериев расчета (т. е. расчета на изгиб, сдвиг, прогиб, боковую опору, или любую их комбинацию).
Калькулятор стальных балок: выбирает самую легкую W-образную стальную балку перекрытия с поперечной опорой после ввода значений пролета, шага, предела текучести, критериев прогиба и расчетных критериев (т. е. расчет на изгиб, сдвиг, прогиб или любое их сочетание). из них).
Калькулятор интегрированных тавровых балок, балок и односторонних плит из железобетона: Новое и улучшенное! Находит требуемые размеры арматурных стержней или расстояние между стержнями для интегрированных систем ферм, балок и односторонних плит, где балки и фермы спроектированы как тавровые балки на основе спецификации временных и постоянных нагрузок. Старый калькулятор, который вычисляет только требуемую площадь стержней и расстояние между арматурными стержнями для перекрытий, можно найти здесь.
Калькулятор расстояния между железобетонными хомутами: Определяет требуемое расстояние между хомутами (стальной стенкой) для железобетонных или тавровых балок. Либо «Империал», либо «С.И.» можно использовать единицы. Также доступно более подробное обсуждение темы.
Соединения:
Калькулятор мощности крепежа для дерева: Определяет мощность болтов, шурупов или гвоздей, используемых в качестве крепежа в деревянных конструкциях с использованием деревянных или стальных боковых пластин.
Калькулятор нагрузки на болты из высокопрочной стали: Определяет нагрузку на болты из высокопрочной стали при сдвиге.
Системы:
Железобетон Интегрированный калькулятор тавровых балок, односторонних перекрытий и колонн: находит требуемую площадь арматурных стержней (или расстояние) и выбирает стержни для тавровых балок, односторонних плит и колонн в типичном бетонное здание.

Монтаж кровельных окон видео: Видео: Установка мансардного окна Roto

Ремонт кровли мягкой видео: Видео о ремонте мягкой кровли

29 июня, 2018 alexxlab

Как исправить уровень строительный: Как проверить ручной строительный уровень

Содержание Как проверить ручной строительный уровеньПроверяем поверхностиПроверяем пузырьковый уровеньПроверка точности строительного пузырькового уровня |Это тоже интересно:Лучшие способы проверки строительного уровняРазновидности строительных уровнейПлюсы и минусы пузырькового уровняКак проверить точностьКак сделать выбор в магазинеКак настроить уровеньКак проверить строительный уровень на точность в домашних условиях: правильная настройка уровняКонструктивные особенностиПрименение и конструкция уровнейКак выбрать строительный уровень?Рейтинг строительных уровнейСоветы, полезные […]

Читать далее

2 июня, 1970 alexxlab

М28 уникма: Металлочерепица М28 / T05. Для тех, кому нужна особенная металлочерепица

Содержание Металлочерепица УНИКМА-М28 в Брянске — Салон Кровли «Ваш Дом»Основные характеристики стали с покрытиемM28 – металлочерепица из оцинкованной стали.Металлочерепица М28Металлочерепица М28 и её преимуществаПреимущества металлочерепицы М28:Почему она красивееПочему она прочнееПочему она долговечнееПочему она маркирована28 — Кровля и фасадыПокрытия:Фирма «Уникма» начала выпуск металлочерепицы М28 с новым покрытием PurexМ28Каталог цвета для металлочерепицы M28Лучшая металлочерепица — какую маталлочерепицу […]

Читать далее

30 апреля, 2020 alexxlab

Краска в д это – Что такое вододисперсионная краска

Содержание Что такое вододисперсионная краскаЧто это за краска?Ключевые преимущества и особенностиСферы примененияОсновные видыЧто такое вододисперсионная краска – ее преимущества и особенностиЧто это за краска?Ключевые преимущества и особенностиСферы примененияОсновные видыВодоэмульсионная или вододисперсионная краска — отличия и особенностиСвойства и особенности обоих видовВодоэмульсионкиВододисперсионкиВажные особенности и преимущества красок на водной основеА есть ли различияВододисперсионная краска. Виды ее и отличия […]

Читать далее

Калькулятор балки: Расчет балки на прогиб и прочность