Как вычесть угол: Калькулятор градусов онлайн ° ’ ”. – Углы прямоугольного треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Как найти углы прямоугольного треугольника

Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для угла α:
• угол β
• длины катетов a и b
• длину гипотенузы (с) и длину одного из катетов
• для угла β:
• угол α
• длины катетов a и b
• длину гипотенузы (с) и длину одного из катетов

Введите их в соответствующие поля и получите результат.

Найти угол α зная угол β и наоборот

Формула

α = 90° — β

β = 90° — α

Найти углы прямоугольного треугольника зная катеты

Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a

Формулы

tg(β) = ^b/_a

или так:

α = arctg(^a/_b)

β = arctg(^b/_a)

Пример

Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:

∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°

∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°

Найти углы прямоугольного треугольника по катету и гипотенузе

Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?

Формулы

sin(α) = ^a/_c

sin(β) = ^b/_c

cos(α) = ^b/_c

cos(β) = ^a/_c

или так:

α = arcsin(^a/_c) = arccos(^b/_c)

β = arcsin(^b/_c) = arccos(^a/_c)

Пример

Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:

∠α = arccos(3/6) = arccos(0.5) = 60°

∠β = arcsin(3/6) = arcsin(0.5) = 30°

См. также

Решение прямоугольного треугольника | Формулы и расчеты онлайн

Решение прямоугольного треугольника по двум сторонам

Если даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме Пифагора. Острые углы определяются по формулам тригонометрических функций острого угла — Синус угла — sin(A), Косинус угла — cos(A), Тангенс угла — tg(A), Котангенс угла — ctg(A), Секанс угла — sec(A), Косеканс угла — cosec(A).

Решение прямоугольного треугольника

Если известны катет a и гипотенуза c

Второй катет b определится по теореме Пифагора:

\[ b = \sqrt{c^2 — a^2} \]

Угол A определится по формуле синуса:

\[ \sin(A) = \frac{a}{c} \]

Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:

\[ B = 180° — 90° — A \]

Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и гипотенуза)

Если известны катеты a и b

Гипотенуза с определится по теореме Пифагора:

\[ c = \sqrt{a^2 + b^2} \]

Угол A определится по формуле тангенса:

\[ \tg(A) = \frac{a}{b} \]

Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:

\[ B = 180° — 90° — A \]

Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и катет)

Решение прямоугольного треугольника по стороне и острому углу

Если дан острый угол A, то B найдется по формуле:

\[ B = 90° — A \]

Стороны можно найти по следующим формулам:

Вычислить, найти решение прямоугольного треугольника если известны катет a и противолежащий угол A

Здесь все углы мы найдем по формуле (7). Гипотенузу по формуле (14) и второй катет по формуле (16).

В помощь студенту

Как найти стороны прямоугольного треугольника

Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
• длины катетов a и b
• длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
• длину гипотенузы (с) и длину одного из катетов
• длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
• длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
• длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

c² = a² + b²

следовательно: c = √a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √3² + 4² = √9 + 16 = √25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

c = ^a/_cos(β) = ^b/_cos(α)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

c = ^a/_sin(α) = ^b/_sin(β)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

a = √c² — b²

b = √c² — a²

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √5² — 4² = √25 — 16 = √9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

a = c ⋅ cos(β)

b = c ⋅ cos(α)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

a = c ⋅ sin(α)

b = c ⋅ sin(β)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

a = b ⋅ tg(α)

b = a ⋅ tg(β)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

a = b / tg(β)

b = a / tg(α)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см

См. также

Как высчитать угол 90 градусов рулеткой

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол?

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника. Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.

Теорема Пифагора

Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: ”В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов” ( a 2 + b 2 = с 2 ), где a и b – катеты, а с – гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.

А теперь вернемся к нашим замерам и применим теорему на практике.

Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.

Египетский треугольник

Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник – прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?

a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5.

Как проверить угол с помощью египетского треугольника?

Отмерьте на одной стене отрезок длиной 3 метра, а на другой – отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.

Как отмерить угол, используя рулетку

Можно самостоятельно смастерить угольник для замера углов:

1. Соединяем две рейки одна перпендикулярно другой.
2. Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
3. Прибиваем третью рейку к одной отметке.
4. Измеряем гипотенузу, прибиваем рейку ко второй метке.
5. Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
6. Обрезаем лишние концы.

Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте. Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.

Строительная рулетка для электрика является таким же обязательным инструментом, как и индикатор напряжения. Даже у тех профессионалов, которые имеют в комплекте инструмента осепостроители и лазерные дальномеры, непременно в подсумке всегда присутствует обыкновенная рулетка.

Без нее не обойтись ни при разметке трасс электропроводки, ни при монтаже подрозетников.
Однако далеко не каждый знаком со всеми секретами и дополнительными возможностями при использовании строительной рулетки.

У нее оказывается очень много скрытых способностей, которые помогут вам заменить сразу несколько инструментов и значительно сэкономить время на ремонт.

Кстати, один из важных советов, для тех кто пользуется китайскими дешевыми рулетками заключается в следующем — если у вас именно такой экземпляр, то старайтесь все замеры делать одной рулеткой.

Один и тот же размер при измерении разными рулетками может не совпадать.

Один знакомый измерял расстояние стен в доме китайским инструментом, а в магазине при покупке материалов воспользовался их рулеткой. В итоге, дома очень был удивлен результатом покупки.

Подвижный зацеп сегодня встречается почти на каждой рулетке. И эта штука вовсе не для того, чтобы удобно спину почесать 🙂
Новички вообще нередко думают, что это какой-то брак. Какая в итоге будет точность, если один из ключевых элементов болтается и не закреплен надежно? Некоторые даже умудряются его заклепать сразу же после покупки.

Оказывается, что подвижный зацеп это необходимость, без которой вообще не возможна нормальная работа.
Объясняется это тем, что измерения рулеткой можно производить двумя способами:

от предмета

Когда вы измеряете расстояние от предмета, зацеп выполняет роль нулевой точки. При измерении с захватом предмета, зацеп выдвигается на свою толщину. Тем самым нулевая отметка снова совпадает с краем предмета.

Поэтому не стоит сматывать строительную рулетку с эффектным щелчком в конце, тем самым вы только сократите срок ее службы.

Еще во многих моделях лента рулетки в самом начале на расстоянии 2,5см имеет отверстие. Сделано оно не просто так, а опять же чтобы облегчить вашу работу в одиночку.
Когда не за что закрепиться зацепом или неудобно им пользоваться из-за косой поверхности, простым шилом или гвоздиком через отверстие намертво закрепляете ленту и растягиваете ее на любую длину.

Воспользовавшись таким отверстием в рулетке вам не придется применять подобные захваты как на фото ниже. А всю работу по разметке можно легко проделывать без напарника.

Как вы понимаете при замерах в углах, серединой ленты рулетки очень трудно залезть непосредственно в угол. Также неудобно делать точные измерения в дверном или оконном проеме.
Поэтому в том случае когда нужно замерить проем, используйте корпус как продолжение рулетки.

На внешней стороне самой рулетки указан размер корпуса, который и нужно прибавить к показаниям ленты при измерении.

Если такого размера на корпус не нанесено, никто вам не мешает самостоятельно его измерить и написать в любом удобном месте.

Есть еще способ сделать подобные замеры с применением малярной ленты. Наклеиваете на поверхность кусочек ленты и производите два измерения в противоположных направлениях.

При этом карандашом в качестве метки лучше ставить галочки, а не простые черточки. Они будут визуально точнее показывать отметку. Тогда как черточка может быть нарисована криво, что и вызовет погрешность.

Проделав два измерения нужно сложить результаты и получите точный размер.

На многих зацепах рулетка имеет небольшое отверстие. Этим отверстием удобно зацепиться за шуруп или гвоздь. После этого зацеп уже никуда не соскочит.

Особенно это полезно, когда вы в одиночку проводите измерения на больших расстояниях. Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.

Еще при помощи этого разъема в зацепе очень удобно рисовать окружности. Не нужно при себе иметь ни циркуля, ни транспортира.

В некоторых моделях зацепы выполняют магнитными. Помимо прямого их назначения, такими зацепами удобно поднимать упавшие предметы не слезая со стремянки.

Если применить небольшую доработку к дешевой рулетке, то из одного инструмента получается отличное приспособление для разметки.
Берете ножку циркуля, которая применяется с простыми карандашами, и закрепляете ее на внешней стороне рулетки.

Эту конструкцию можно сделать съемной, или вообще приспособить под отдельную рулетку.

Таким устройством очень удобно делать различные отметки или пользоваться им как рейсмусом.

А при использовании шурупа легко рисуются окружности нужного диаметра.

Если вы работаете с гипсокартоном или другой поверхностью, которую можно безопасно поцарапать, то рулетку стоит переделать под еще одну возможность. Надфилем на зацепе делаете зазубрины.

После чего с помощью этого зацепа легко делаются отметки на поверхности. При этом уже даже не обязательно чтобы под рукой был карандаш.

Внешнюю часть рулетки легко превратить в мини напоминалку или поверхность для записей. Берете малярную ленту и наклеиваете сбоку рулетки.

Если нет под рукой малярки, то можно писать прямо на самом корпусе.
Правда для этого, сначала надо пройтись по поверхности наждачкой нулевкой.

Так вы сделаете ее несколько бархатной, после чего надписи будут наноситься горазд легче.

Писать конечно нужно карандашом, после чего все это легко стирается резинкой.

С помощью строительной рулетки очень легко разделить любое число с точность до миллиметра пополам, не прибегая к услугам калькулятора.

Берете размер на рулетке, к примеру 116см — и сложив ленту пополам совмещаете с ним нулевую отметку, там где верхний зацеп.

Ровно в месте перегиба и будет требуемый результат — 58см.

Этим же способом можно не только делить, но и отнимать. Например общая длина стенки у вас 2м 11см, а распредкоробка находится от первого края на расстоянии в 1м 38см. Вам нужно быстро узнать сколько остается от этой распредкоробки до другого края стены, чтобы отмерить кабель канал.

Вытягиваете ленту на 2м 11см и складываете ее пополам.

Затем ищете отметку в 1м 38см. Как раз напротив нее, на второй половине ленты, и будет показано нужное вам расстояние — 73см.

Используя обыкновенную ленту рулетки можно легко разделить рабочую поверхность или заготовку на требуемое количество равных частей. Данный метод подходит в первую очередь для больших поверхностей — для труб или кабель каналов уже не сработает.

Как вы поступаете обычно? Замеряете общую длину или ширину, затем делаете вычисления и делите расстояние на нужное количество частей. После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.

Оказывается все это можно проделать без калькулятора и даже без вычислений. Берете на рулетке число, которое больше чем ширина заготовки, и при этом кратно той величине, на которое вы хотите разделить расстояние.

Например ширина доски 17см, а вам ее нужно разделить на четыре равные части. Сдвигаете рулетку по диагонали до ближайшей отметки в 20см. После чего легко делите эти 20см на 4 и отмечаете метки на расстояниях 5см, 10см, 15см, 20см.

В итоге вы всего одним движением рулетки разделили поверхность на нужное количество частей.

Захотели поделить на 6 частей — ничего сложного. Можно сдвинуть диагональ до 30см и проделать то же самое.

Еще рулеткой на круглой трубе можно точно отмерить поперечный срез. Для этого плотно прижимаете по периметру трубы ленту, совместив концы. Если совместили ровно, никак иначе как под углом в 90 градусов она не ляжет.

Чем шире лента рулетки, тем предпочтительней. Проделать такой же фокус можно и с простым листком бумаги.

Когда невозможно измерить диаметр трубы или заготовки с торца, опять поможет строительная рулетка и геометрия. Обхватываете трубу лентой и измеряете ее окружность. После чего полученный результат нужно разделить на число Пи = 3,14. Это и будет необходимый диаметр.

Еще раз применив знания геометрии, строительной рулеткой без угольников и других инструментов можно проверить точность прямого угла. Как вы знаете из школьного курса — сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.

Берете любую поверхность где должен быть прямой угол, например две стены комнаты. Отмеряете рулеткой в одну сторону 30см, а в другую 40см и ставите метки. Если угол действительно прямой и строители не накосячили, то соединив эти две метки по гипотенузе, вы должны получить на рулетке расстояние ровно в 50см.

Такой метод применим к любым поверхностям и изделиям. Главное что вам нужно соблюдать при измерении — это пропорции 3 -4 -5.

Если вы еще не приобрели себе рулетку, подобрать необходимую модель и ознакомиться с текущими ценами на них можно здесь.

Как вычислить угол конуса? — Общий

starik12 Вы вообще умеете пользоваться таблицами Брадиса? Судя по тому, что вам втолковывают уже несколько дней вы первый раз о них слышали. А зря, дюже полезная книжечка.

1. Берём формулу расчёта которую вам уже дали в 5 или 9 сообщении.

2. Считаем и получаем данные, что tg@= 0.125

3 Берём в руки таблицу Брадиса и смотрим на страницу Тангенсы.

4 Ближайшие к вашим данным это цифры 0.1246 и 0.1263 стоящие в строке напротив левого вертикального столбца где написан угол 7 градусов, записываем его.

Далее высчитываем минуты.

5. До вашего значения 0.1250 первому числу в пункте 4 не хватает 0.0004, а второе больше на 0.0013.

Смотрим на крайние правые колонки. Напротив вашей строки видим цифры 3 6 9. Это поправки на которые надо надбавить или убавить данные таблицы, что бы они совпадали с вашим числом (0.1250) и обозначают они четвёртую цифру после запятой. Наиболее подходит поправка 3 как наиболее близкая к числу 0.1246.

6. Смотрим вертикально вверх от числа 0.1246, видим цифру 6. Это ваши минуты. Запимываем. Далее воспользуемся поправкой 3 про которую я писал в 4 пункте. Смотрим вверх от нее и видим цифру 1. Это число надо прибавить к вашим минутам. Получаем 6+1=7минут. Записываем к вашим градусам.

7. Далее высчитываем секунды. До ваших данных 0.1250 даже с учётом поправок не хватает 0.0001.

Смотрим на поправки. Поправка 4 составляют 1/3 часть между поправками 3 и 6. Смотрим вверх. Там поправка 3 означает 1 минуту, а поправка 6 означает 2 минуты значит поправка 4 означает на 1/3 больше 1минуты, что в конечном итоге составляет 20 секунд.

8. А вот теперь смотрим на бумажку и пишем данные полученные в пунктах 4, 6, и 7. Получаем, что данный ваш угол равен 7 градусов 7 минут 20 секунд.

Потом после того как вы выставите можно проверить способом который предложил Alex_IZA. Я так всегда делаю. Пару тончайших рисок на цилиндрической поверхности и часиками можно спокойно проверить.

Ужас, писал 15 минут, хотя считается это дело в течение 10 -15 секунд.

Угловой размер, линейный размер и расстояние

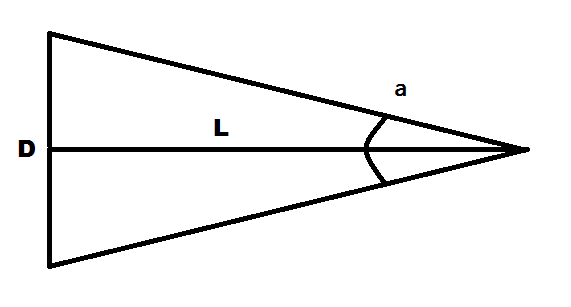
Угловой размер — это угол между линиями, соединяющими диаметрально противоположные точки измеряемого объекта и глаз наблюдателя.
Посмотрим на рисунок: здесь отрезок D — измеряемый объект, отрезок L — линия наблюдения, перпендикулярная отрезку D и являющаяся его серединным перпендикуляром, и угол а — угловой размер отрезка D.
Очевидные соотношения между величинами (вспомним тригонометрию):

Таким образом, наблюдатель, зная, например, линейный размер объекта, по угловому размеру объекта может определить расстояние до него. Помню, раньше для этих целей военные бинокли снабжали специальными риcками для определения углового размера.

Ну и обратные задачи тоже имеют место — зная, например, расстояние и линейный размер объекта, можно определить его угловой размер; и наконец, зная расстояние и угловой размер, можно определить линейный размер. Последние задачи актуальны для астрономии. Там используют термин угловой диаметр — то есть видимый диаметр небесного тела, выраженный в угловых мерах.

Ниже калькуляторы, рассчитывающие неизвестные по всем соотношениям. В качестве данных по умолчанию используется расстояние от Земли до Солнца, диаметр Солнца и средний угловой диаметр Солнца, наблюдаемого с Земли.

Расстояние по угловому и линейному размеру

Знаков после запятой: 2

save Сохранить share Поделиться extension Виджет

Линейный размер по угловому размеру и расстоянию

Знаков после запятой: 2

Линейный размер

save Сохранить share Поделиться extension Виджет

Угловой размер по расстоянию и линейному размеру

Угловой размер

save Сохранить share Поделиться extension Виджет

Катет «A» и угол «α» прямоугольного треугольника

Зная один из катетов в прямоугольном треугольнике, можно найти второй катет и гипотенузу используя тригонометрические отношения – синус и тангенс известного угла. Так как отношение противолежащего углу катета к гипотенузе равно синусу этого угла, следовательно, чтобы найти гипотенузу нужно катет разделить на синус угла. a/c=sin⁡α c=a/sin⁡α

Второй катет можно найти из тангенса известного угла, как отношение известного катета к тангенсу. a/b=tan⁡α b=a/tan⁡α

Чтобы вычислить неизвестный угол в прямоугольном треугольнике нужно из 90 градусов вычесть величину угла α. β=90°-α

Периметр и площадь прямоугольного треугольника через катет и противолежащий ему угол можно выразить, подставив полученные ранее выражения для второго катета и гипотенузы в формулы. P=a+b+c=a+a/tan⁡α +a/sin⁡α =a tan⁡α sin⁡α+a sin⁡α+a tan⁡α S=ab/2=a^2/(2 tan⁡α )

Вычислить высоту также можно через тригонометрические отношения, но уже во внутреннем прямоугольном треугольнике со стороной a, который она образует. Для этого нужно сторону a, как гипотенузу такого треугольника умножить на синус угла β или косинус α, так как согласно тригонометрическим тождествам они равнозначны. (рис. 79.2) h=a cos⁡α

Медиана гипотенузы равна половине гипотенузы или известному катету a, деленному на два синуса α. Чтобы найти медианы катетов, приведем формулы к соответствующему виду для известной стороны и углы. (рис.79.3) m_с=c/2=a/(2 sin⁡α ) m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2=√(4a^2+a^2/tan^2⁡α )/2=(a√(4 tan^2⁡α+1))/(2 tan⁡α ) m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4b^2+a^2 )/2=√(4b^2+c^2-b^2 )/2=√(3 a^2/tan^2⁡α +a^2/sin^2⁡α )/2=√((3a^2 sin^2⁡α+a^2 tan^2⁡α)/(tan^2⁡α sin^2⁡α ))/2=(a√(3 sin^2⁡α+tan^2⁡α ))/(2 tan⁡α sin⁡α )

Так как биссектрисой прямого угла в треугольнике является произведение двух сторон и корня из двух, деленное на сумму этих сторон, то заменив один из катетов на отношение известного катета к тангенсу, получаем следующее выражение. Аналогично, подставив отношение во вторую и третью формулы, можно вычислить биссектрисы углов α и β. (рис.79.4) l_с=(a a/tan⁡α √2)/(a+a/tan⁡α )=(a^2 √2)/(a tan⁡α+a)=(a√2)/(tan⁡α+1) l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b+c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(a/tan⁡α √(2c(a/tan⁡α +c) ))/(a/tan⁡α +c)=(a√(2c(a/tan⁡α +c) ))/(a+c tan⁡α ) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(a√(2c(a+a/sin⁡α ) ))/(a+a/sin⁡α )=(a sin⁡α √(2c(a+a/sin⁡α ) ))/(a sin⁡α+a)

Средняя линия проходит параллельно одной из сторон треугольника, при этом образуя еще один подобный прямоугольный треугольник с такими же по величине углами, в котором все стороны в два раза меньше, чем у изначального. Исходя из этого, средние линии можно найти по следующим формулам, зная только катет и противолежащий ему угол. (рис.79.7) M_a=a/2 M_b=b/2=a/(2 tan⁡α ) M_c=c/2=a/(2 sin⁡α )

Радиус вписанной окружности равен разности катетов и гипотенузы, деленной на два, а чтобы найти радиус описанной окружности, нужно разделить на два гипотенузу. Заменяем второй катет и гипотенузу на отношения катета a к синусу и тангенсу соответственно. (рис. 79.5, 79.6) r=(a+b-c)/2=(a+a/tan⁡α -a/sin⁡α )/2=(a tan⁡α sin⁡α+a sin⁡α-a tan⁡α)/(2 tan⁡α sin⁡α ) R=c/2=a/2sin⁡α